基于直方图的隐私键-值数据收集算法
2021-04-01张啸剑徐雅鑫孟小峰
张啸剑 徐雅鑫 付 楠 孟小峰
1(河南财经政法大学计算机与信息工程学院 郑州 450002) 2(中国人民大学信息学院 北京 100872)
(xjzhang82@ruc.edu.cn)
移动互联网环境下的新兴技术快速发展与应用,使得键-值(key-value)数据的获取与收集变得尤为容易,例如网购、健康医疗、金融等数据的收集与分析.键-值数据收集与分析能够提升产品服务与设备服务的质量,以及向用户提供个性化的体验.然而,键-值数据通常蕴含着丰富的个人敏感信息,在提供给收集者或者第三方应用的同时,个人的敏感信息有可能被泄露.表1为某不可信购物网站收集用户购买与评分的记录.通过表1中键的频率以及键所对应值的均值分析,可以学习出用户的购物行为模式与偏好.例如,商品k2的频率为2,k2所对应值的均值为0.61.不可信收集者分析出k2的频率之后,即可对表1中的用户进行统计攻击.因此,在此情景下,用户无法控制自己的隐私数据.本地差分隐私保护技术的出现有效地解决了此类矛盾.该技术允许每个用户扰动自身数据之后再响应收集者的需求.
目前基于本地差分隐私的键-值收集算法包括PrivKV[1],KVUE[2],KVOH[2],PCKV-GRR[3],LDPKV[4].PrivKV,KVUE,KVOH,LDPKV算法基于键的整个值域进行编码,利用简单随机抽样技术减少收集者与用户之间的通信代价.然而,这4种算法均没有考虑到键的值域稀疏性与偏斜性问题.例如,假设表1中商品的值域为7.以u3为例,对其键编码之后可以获得长度为7的向量(〈1,0.6〉,〈0,0〉,〈0,0〉,〈0,0〉,〈0,0〉,〈0,0〉,〈0,0〉).基于该向量进行随机抽样时,〈0,0〉以67的概率被抽取到,而〈0,0〉对最终统计结果无效.当键的值域非常大且稀疏时,PrivKV,KVUE,KVOH,LDPKV算法估计误差比较高.
为了解决PrivKV,KVUE,KVOH,LDPKV算法无法应对键的值域稀疏性问题,PCKV-GRR利用填充-抽样[5]技术减少稀疏性带来的影响.其主要思想是利用给定长度截断每个用户所拥有的键-值对集合,然后利用哑元填充那些小于的键-值对集合.例如,表1中用户u2利用=3截断所拥有的键-值对集合后,该集合变成{〈k2,0.42〉,〈k4,0.6〉,},其中为哑元.然而,该算法存在3点不足:
1) 与PrivKV类似,把隐私预算ε分割成ε1与ε2,其中ε1用来本地扰动键,而ε2用来扰动每个键所对应的值;
2) 在设定本地扰动概率时,没有考虑真实键对最终估计的影响,无论键扰动自身还是其他值均设定相同的扰动概率;
若用户直接发送所拥有的键-值对长度,则会导致隐私泄露.此外,如何选择合理的至关重要,直接影响最终键频率与均值的估计精度.例如,以真实稀疏数据TalkingData为例,该数据集中非零键-值对所占的比例仅为6.9%.根据该数据中60 032个用户的键-值对长度分布(如图1所示)可知,98%的用户的键-值对长度小于50.因此,的理想选择区间为[0,50].

Fig. 1 Length distribution of TalkingData key-value pair图1 TalkingData键-值对长度分布
结合文献[1-4]可知,收集与分析键-值数据过程中存在的挑战包括:1)用户在设计本地扰动算法时,如何设置真实键的扰动概率以及维持键与值之间的关联性;2)由于键-值数据的值域通常很大且稀疏,如何设计有效的最优截断长度;3)收集者如何以较小的通信代价收集所有用户的键-值数据.总而言之,目前还没有一个行之有效且满足本地差分隐私的键-值收集与分析算法能够克服上述算法存在的问题.为此,本文基于本地差分隐私技术提出了一种键-值数据收集算法能够兼顾3方面挑战需求.
本文主要贡献有3个方面:
1) 为了解决挑战1,提出一种基于直方图技术的键-值频率与均值估计算法HISKV.不同于PrivKV,KVOH,LDPKV,PCKV-GRR算法,HISKV算法在不分割隐私预算的情况下,利用直方图技术对键-值对进行整体扰动,进而维持了键-值之间的关联性.同时,对于真实的键分配较大的本地扰动概率.
2) 为了有效解决挑战2与挑战3,提出了一种最优截断算法来寻找截断长度.不同于PCKV-GRR算法中的经验设置,HISKV利用用户分组策略与部分隐私预算估计.结合利用填充-抽样技术处理键值域的稀疏性问题.
3) 理论分析了HISKV算法满足ε-本地差分隐私,以及频率与均值估计的无偏性、误差边界以及最大偏差.通过合成数据与真实数据实验分析,HISKV算法具有较高的可用性.
1 相关工作
本地化差分隐私技术在假设收集者完全不可信的情况下,允许每个用户利用随机响应机制[6]本地扰动自己的数据,并把噪音结果发送给收集者.目前本地化差分隐私研究主要集中于频率估计[7-11]与均值估计[12-15].GRR[7]算法通过直接编码将整个类别属性的值域进行转换,然后对原始值进行本地扰动,而该算法的通信代价与误差均较高.类似于GRR算法,RAPPOR[8]算法结合一元编码与布隆过滤技术把类别属性的整个值域散列到较小的值域中,结合散列值域统计每个类别属性的频率.该算法能够永久性或者及时性地保护每个用户的数据,相应的通信代价较低.基于RAPPOR算法,O-RR[9]算法借助散列编码与分组操作估计整个类别属性的概率分布情况.无论是GRR,RAPPOR及其变种算法,它们的误差均随着值域的增加而增加.OLH[7]算法克服了对值域大小的依赖,该算法利用优化本地散列技术将整个值域Hash到较小地址空间.为了进一步减少通信代价,在较高计算代价的基础上,SHist[10]算法采用随机矩阵投影技术对类别属性值域进行编码,随机扰动1个比特位发送给收集者.此外,LDPMiner[11]算法基于SHist算法研究了集-值数据下的Heavy Hitter问题.不同于上述基于类别属性的频率估计算法,文献[12-15]集中研究[-1,1]中数值均值的估计.Duchi[12-13]算法基于离散化操作,对数值型属性的均值进行估计,并取得较小的通信代价与较低的估计误差.基于Duchi算法,Harmony[14]算法在多维数值元组中随机抽取单个数值并扰动成离散值,然而该算法的估计结果远离了区间[-1,1]中的真实值.PM[15]算法能够将[-1,1]中的真实值扰动到一个连续的区间,并在该连续区间中计算出该扰动值的左右边界.在隐私预算较大时,PM算法的估计精度明显高于Duchi与Harmony算法.
尽管文献[7-15]对类别属性与数值属性上的频率与均值进行了较为系统的研究,然而这些算法很难直接应用于键-值数据,其主要原因在于这些算法没有考虑键-值对之间的关联性.文献[1-4]对键-值数据上的频率与均值估计进行了研究.基于RAPPOR与Harmony算法,PrivKV[1]算法对键-值数据的频率与均值进行了估计,PrivKV与Harmony的主要区别在于PrivKV把扰动后的数值修正操作放到了收集者端.然而,PrivKV算法由于分割隐私预算导致估计精度较低.KVOH[2]与LDPKV[4]算法结合键-值数据值域与扰动输出值域之间的整体映射关系,利用GRR算法对离散化后的键-值对进行扰动.然而,这2种算法的误差易受到值域大小的影响.不同于PrivKV,KVOH,LDPKV 3种算法,PCKV-GRR[3]算法利用填充-抽样操作对原始键-值序列进行截断与抽样,然后再利用GRR算法进行本地扰动.尽管PCKV-GRR在值域较大且稀疏的情况下优于KVOH与PrivKV,但是该算法的误差同样受到值域大小的影响,并且没有顾及到如何设置有效键的扰动概率以及截断长度的计算方法.基于上述分析,本文提出一种基于本地差分隐私的键-值收集与分析算法HISKV,该算法利用直方图技术统一估计键的频率及其均值,利用最优截断长度与填充-抽样技术处理值域稀疏问题.
2 定义与问题
2.1 本地差分隐私
不同于中心化差分隐私保护技术,本地差分隐私技术通常要求用户在本地保护自己的数据,把扰动之后的数据报告给不可信的收集者,从而实现隐私不被泄露.本地差分隐私的形式化定义为:
定义1.ε-本地差分隐私.给定一个随机算法A及其定义域Dom(A)和值域Range(A),若算法A在任意2条不同元组t与t′(t,t′∈Dom(A))上得到相同输出结果o(o∈Range(A))满足不等式:
Pr[A(t)=o]≤eε×Pr[A(t′)=o],
(1)
则A满足ε-本地差分隐私.其中ε为隐私预算,其值越小则算法A的隐私保护程度越高.
2.2 随机应答机制
随机应答机制[6]是实现本地差分隐私的常用技术.在用户发送数据ti之前,对其进行随机扰动.该机制的原始思想是用户在响应敏感的布尔问题时,以概率p真实应答,以q的概率给出相反的应答.为了使随机应答机制满足ε-本地差分隐私,通常设置p=eε(1+eε),q=1(1+eε).目前,基于随机应答机制出现了以GRR为代表的本地扰动算法.给定ki,kj∈{1,2,…,d},GRR算法:
(2)
2.3 问题描述
类似文献[4],给定n个用户U={u1,u2,…,un}和一个收集者,每个用户拥有键-值对集合.K={k1,k2,…,kd}为键的值域,d为该值域大小,V=[-1,1]为键所对应值的值域.Si={〈kj,vj〉|1≤j≤li,kj∈K,vj∈V}为用户ui所拥有的键-值对集合,其中li表示Si的长度.收集者收集所有用户的键-值数据后,通常估计键所对应的频率以及值所对应的均值,具体计算为
(3)
(4)
采用均方误差与相对误差度量fk与μk的估计精度.本文要解决的问题是在设计满足本地差分隐私的频率与均值估计算法的同时,要尽可能获得误差较小的估计结果.
3 基于直方图技术的键-值数据收集算法
3.1 HISKV算法
不同于文献[1-4]中的收集算法,HISKV算法不需要对每个用户的键按照值域进行编码,而是仅对键所对应值进行离散化处理.给定某个键-值对〈k,v〉,只对值v进行离散化操作,结果为
(5)
例如,设〈汉堡,0.4〉为某一个键-值对,则0.4以0.7的概率离散化+1;以0.3的概率离散化为-1.
根据式(5)可知,每个用户所拥有键的对应值均被离散化成2个类别,分别为+1或者-1,而所有的键还保持原来的值.因此,可以在{d,+1}与{d,-1}这2个二维值域内构建相应的直方图来估计键的频率以及所对应值的均值,其中每个键即是直方图的桶.结合桶的频率可以估计每个键的频率及所对应值的均值.如表1所示,用户u1,u2,u3的键-值对经过离散化之后的值为{〈k1,+1〉,〈k2,+1〉,〈k3,-1〉,〈k4,-1〉,〈k5,+1〉},{〈k2,-1〉,〈k4,+1〉},{〈k5,+1〉}.根据d={k1,k2,k3,k4,k5,k6,k7}以及d所对应的值{+1,-1}可获得相应直方图(如图2所示).根据图2可以估计出d中每个键的频率及均值.例如,键k2的频率为23,k2所对应值的均值为1.

Fig. 2 Two-dimensional range histogram图2 二维值域直方图
结合直方图技术的HISKV算法如算法1所示:
算法1.HISKV算法.
输入:n个用户、每个用户所拥有的键-值对集合S={S1,S2,…,Sn}、隐私预算ε、键的值域d;
输出:频率向量f*、均值向量μ*.
①f*←∅,μ*←∅;
② 收集者将n个用户分成2组βn,(1-β)n;
④ for 在[(1-β)n]内的每个用户ui执行步骤⑤~⑥;*每个用户扰动*

LRR_KV(Si,ε,);
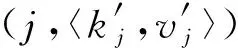
⑦ end for
⑨ ifkj∈[1,2(d+)] then

HISKV算法是基于本地差分隐私解决键的频率以及所对应值的估计问题.首先收集者从n个用户中抽取βn个用户(β为抽取概率)(步骤②).基于βn个用户利用OETL算法估计最优截断长度(步骤③).每个用户结合截断长度对自身所拥有的键值对集合进行截断或者填充.然后再均匀随机抽样一个键-值对本地扰动,并把扰动结果报告给收集者(步骤④~⑦).收集者聚集所有用户的报告值后,估计每个键的频率以及值所对应的均值(步骤⑧~).由LRR_KV算法中的抽样可知,每个用户仅扰动一组键-值对报告给收集者,进而使得收集者与用户之间的通信代价为O(1).接下来阐述LRR_KV与OETL算法,其中LRR_KV算法具体细节如算法2所示:
算法2.LRR_KV算法.
输入:(1-β)n用户中任意ui的键-值集合Si、隐私预算ε、截断长度;
① 〈kj,vj〉←Padding-Sampling(Si,);
②〈kj,±1〉←Discretizing(〈kj,vj〉);
③ if thej-th pair 〈kj,vj〉 is 〈kj,1〉 then

⑤ else if thej-th pair 〈kj,vj〉 is 〈kj,-1〉 then
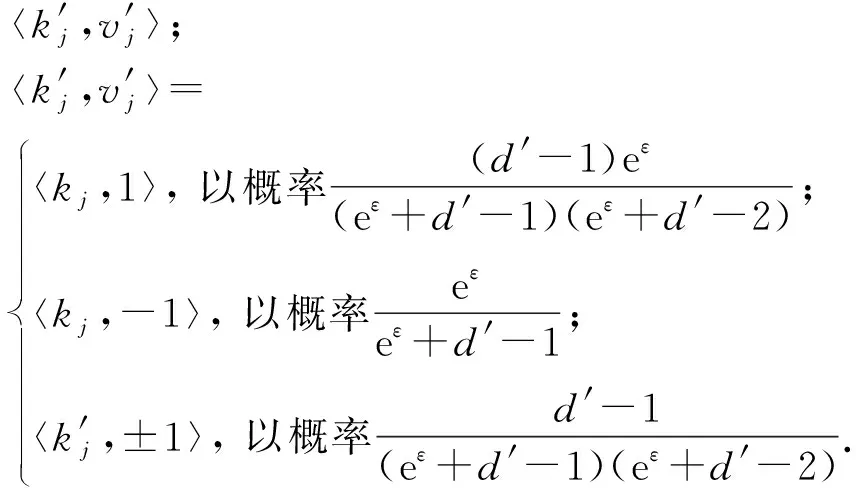
⑦ end if
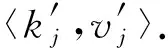
结合LRR_KV算法,用户ui首先利用算法3步骤①对集合Si进行填充-抽样操作,进而获得〈kj,vj〉.结合〈kj,vj〉,用户ui利用式(5)对值vj进行离散化操作(步骤②).然后结合离散化结果〈kj,±1〉进行本地扰动(步骤②~⑦).结合用户ui的键-值对集合Si,LRR_KV算法的具体实现思路如图3所示:

Fig. 3 LRR KV local disturbance图3 LRR_KV本地扰动示意图
根据图3可知,用户ui所抽取的键-值对〈kj,vj〉经过离散化后变成〈kj,1〉或者〈kj,-1〉.以概率p1,q1,q2分别将〈kj,1〉与〈kj,-1〉扰动成4种不同的情况.其中一种情况是〈kj,1〉与〈kj,-1〉以概率p1扰动成自身.由式(2)可知,p1=eε(eε+d′-1),其中,d′=2(d+).如何设置剩余3种的扰动概率是一个大的挑战.文献[3]中PCKV-GRR算法在相应参数取得最优时,剩余3种概率均取值为1(eε+d′-1).然而,该算法却忽略一种事实,即不论〈kj,1〉以概率q1扰动成〈kj,-1〉或者〈kj,-1〉以概率q1扰动成〈kj,1〉,键kj并没有被扰动成值域d′中的其他值.此种情况对键kj的频率及其所对应值的均值估计均有效.因此,概率q1的值不应该取平均值,应该倾向性地取较大的值.由定义1可知下式成立:
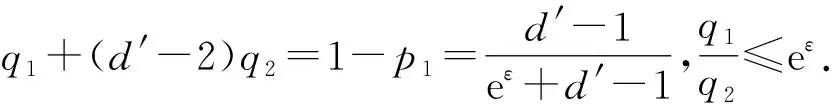
影响LRR_KV算法本地扰动效果包括2个因素:Padding-Sampling算法的设计以及如何获得最优截断长度.接下来结合文献[5]设计填充-抽样算法.
算法3.Padding-Sampling算法.
输入:Si、截断长度;
输出:所抽取的键-值对(kj,vj).
① ifli>then*li表示Si的长度*
②ui不放回地从Si,随机采样个键值对,得到抽取个键-值对*
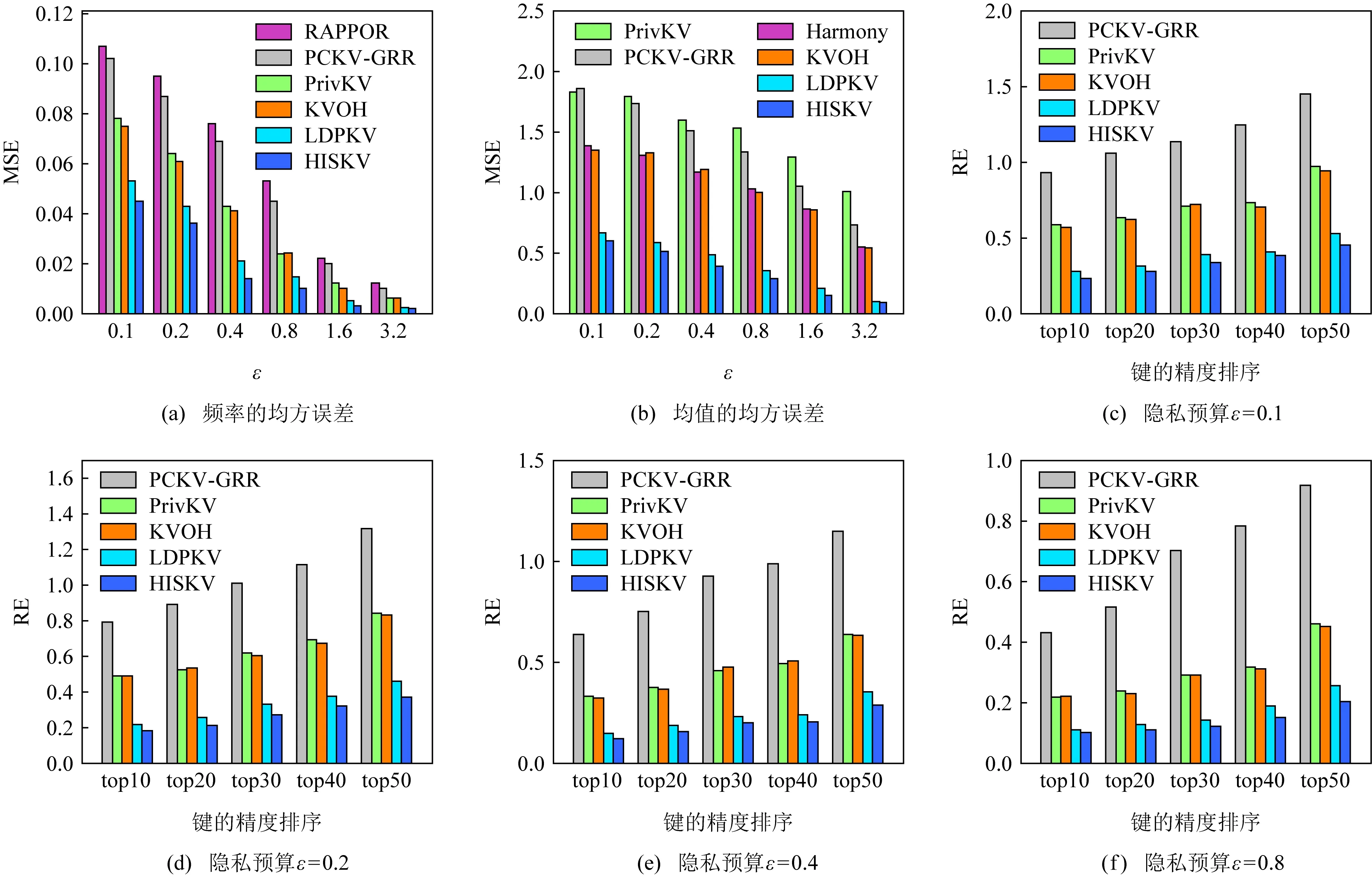
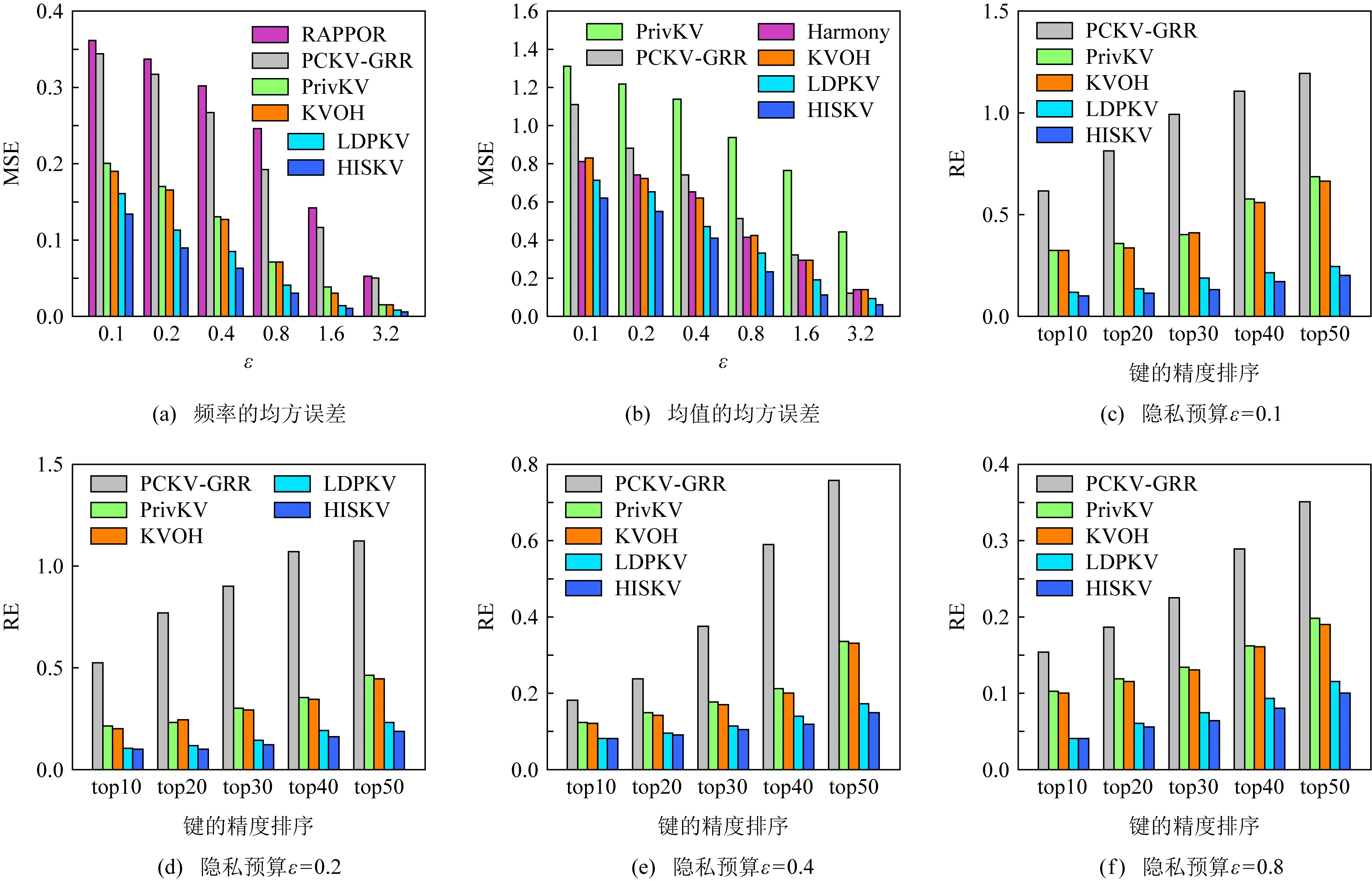
③ else ifli ④ui用-li个从{〈1,0〉,〈2,0〉,…,〈l,0〉}集合采样的哑元填充Si,得到 ⑥ end if ⑦ return 〈kj,vj〉. 用户ui利用Si的长度li与截断长度比较.如果li>,则从Si中无放回地抽取个键-值对形成(步骤①②);否则,从哑元键-值对集合{〈1,0〉,〈2,0〉,…,〈l,0〉}中随机抽取-li个键-值对填充Si,并获得(步骤③④).结合用户以概率1抽取一个键-值对〈kj,vj〉. 算法4.OETL算法. 输入:n、β、ε、键的值域d; ① for 在[βn]的每个用户ui执行步骤②~③;*每个用户扰动* ④ end for ⑧ end for βn中的每个用户利用GRR算法本地扰动自己键-值对长度li,步骤①~④发送给收集者;步骤⑤~⑧收集者计算并修正每个长度的计数;步骤⑨利用第90个百分位数求解后;步骤⑩收集者将发送给(1-β)n中的每个用户. 本节主要从本地差分隐私阐述HISKV算法的隐私性以及无偏性估计、方差及其最大偏差来阐述其可用性.从算法1可知,HISKV算法采用用户分组的形式分别估计频率与均值(LRR_KV算法)以及最优截断长度(OETL算法). 定理1.OETL算法满足ε-本地差分隐私. 证明. 结合[βn]集合中用户所给定任意的li与lj,算法OETL的输出为l′,则不等式成立: 则OETL算法满足ε-本地差分隐私. 证毕. 定理2.LRR_KV算法满足ε-本地差分隐私. 1) 当〈k*,v*〉=〈kj,1〉时,根据定义1可知: 2) 当〈k*,v*〉=〈kj,-1〉时,类似于第1种情况: 通过4种情况可知LRR_KV算法满足ε-本地差分隐私. 证毕. 由定理1与定理2以及差分隐私的序列组合性质可知,HISKV收集键-值数据的过程满足本地差分隐私.HISKV的可用性主要从LRR_KV算法与OETL算法的误差来度量.OETL算法的误差主要来自于GRR算法的本地扰动操作,根据文献[7]可知,OETL算法产生的方差为βn(eε+d-2)(eε-1)2.LRR_KV算法的可用性主要从无偏性、方差、最大偏差来度量.尽管收集者可以估计出键k的频率以及所对应值的均值但由于LRR_KV算法的本地扰动使得与会偏离真实值.而我们期望与均要满足无偏性,即与成立. 根据二项分布构造极大似然函数: (6) (7) 将式(7)带入式(6)可推理出: (8) 证毕. (9) (10) 证毕. 其中n′=(1-β)n. (11) (12) 证毕. 证毕. 至少以概率1-η成立,其中n为用户个数,为最优截断长度,β为用户分组抽样率. 则可知: (13) 证毕. 证毕. 文献[4]结论部分所给出的未来研究点正是本文的研究工作。因此,从实验平台、实验数据集以及隐私参数ε的设置均与文献[4]保持一致。实验平台是4核Intel i7-4790 CPU(4 GHz),8 GB内存,Win7系统,Python实现所有算法.采用TalkingData,JData,GAUSS,LNR四个数据集验证文中相关算法.4个数据集具体细节如表2所示: Table 2 Characteristics of Datasets 其中GAUSS和LNR这2个数据集为合成数据集,键和值分别遵循高斯和线性分布.TalkingData是从与移动应用的SDK中收集而得,包含60 822个设备和306类应用程序.JData来自于JD.com,包含2016年的5 060万条销售记录,该数据集记录了2016年间105 180个用户对442个品牌的5 060万条购买记录. 隐私参数ε分别取值为0.1,0.2,0.4,0.8,1.6,3.2.此外,实验分别对4个数据集中频率最高的top10, top20,top30,top40,top50的键值进行统计,在每种情况下进行500次实验并求取平均值作为最终的计算结果. 在文献[4]中,我们分别实现了LDPKV,PrivKV,KVOH,RAPPOR以及Harmony算法,并结合MSE与RE进行了综合对比分析.因此,本文主要对比HISKV算法与上述6种算法的性能. 1) 基于TalkingData数据集的多种算法的MSE和RE值比较. 图4(a)~(f)描述了HISKV,PCKV-GRR,PrivKV,KVOH,LDPKV,RAPPOR,Harmony算法的MSE值和RE值的比较结果.由图4(a)的实验结果可以发现,当ε从0.1变化到3.2时,6种算法的MSE值均减少,而HISKV算法的精度优于其他5种算法.当ε=1.6时,HISKV算法的精度是PCKV-GRR算法的近4倍,是PrivKV和KVOH算法的将近3倍,是LDPKV算法的将近1倍.尽管文献[4]中提到LDPKV算法优于PrivKV和KVOH算法,然而由于该算法没有考虑到键-值的稀疏性(如图1所示),过多的〈0, 0〉对使得该算法的MSE大于HISKV算法. Fig. 4 The key-value frequency and mean estimation of TalkingData图4 基于TalkingData的键-值频率与均值估计结果 由图4(c)~(f)可知,当ε固定,键的数目从top10增加到top50时,相应算法的RE值均增大,但HISKV算法的精度却优于其他4种算法,其原因在于HISKV算法利用最优截断长度削弱了键-值值域稀疏带来的影响.由图4(b)中6种算法的均值MSE比较结果可知,当ε从0.1变化到3.2时,6种算法的均值MSE均呈现下降趋势,而HISKV算法估计出的均值精度明显优于其他5种算法.当ε=1.6时,HISKV算法的均值精度是LDPKV算法的将近1倍.其主要原因在于HISKV算法利用直方图将键-值对进行统一编码扰动,避免了隐私预算的分割,合理增大了扰动成真实键的本地扰动概率.此外,HISKV算法利用截断-抽样技术避免了键-值稀疏性带来的影响,实现了隐私增强. 2) 基于JData数据集的多种算法的MSE和RE值比较. 图5(a)~(f)描述了JData数据集上7种算法的MSE值和RE值的比较结果.根据图5(a)的实验结果可知,当ε从0.1变化到3.2时,6种算法的MSE值均减少.当ε=1.6时,HISKV算法的精度是PCKV-GRR算法的近6倍,是PrivKV和KVOH算法的将近3倍,是LDPKV的将近2倍.其主要原因是PCKV-GRR算法没有顾及真实键本地扰动概率的倾向性设置问题,PrivKV和KVOH算法隐私预算进行分割,LDPKV算法没有考虑值域稀疏性带来的影响.图5(b)描述了HISKV算法与其他5种算法有关均值MSE值的比较.当ε从0.1变化到3.2时,HISKV算法的均值精度优于其他5种算法.当ε=0.8时,HISKV算法的均值精度是PrivKV算法的近4倍,是PCKV-GRR算法的近3倍,是Harmony与KVOH的近2倍,是LDPKV算法的近1倍.在固定ε且变换top10到top50的情况下,HISKV算法同样优于其他4种算法.其主要原因是HISKV算法利用抽样-截断技术、本地扰动概率的倾向性设置以及隐私预算不分割策略提升了键-值的频率与均值估计精度. Fig. 5 The key-value frequency and mean estimation of JData图5 基于JData的键-值频率与均值估计结果 Fig. 6 The key-value frequency and mean estimation of LNR图6 基于LNR的键-值频率与均值估计结果 Fig. 7 The key-value frequency and mean estimation of GAUSS图7 基于GAUSS的键-值频率与均值估计结果 3) 基于LNR,GAUSS数据集的多种算法的MSE和RE值比较. 图6和图7描述了7种算法基于LNR与GAUSS合成数据集上的MSE与RE的对比结果.在百万级别的数据上,当ε从0.1变化到3.2时,HISKV算法的精度优于其他6种算法,如图6(a)、图6(b)、图7(a)、图7(b)所示.文献[4]给出了LDPKV算法在LNR与GAUSS数据集上优于PrivKV,KVOH,RAPPOR以及Harmony算法.而本文的HISKV算法却明显有LDPKV算法,其主要原因在于LNR与GAUSS数据集中同样存在键-值的稀疏性问题,而HISKV算法的最优截断长度技术却可以有效减弱键-值稀疏性带来的影响.此外,当固定键值的个数且ε从0.1变化到0.8时,所有算法在LNR与GAUSS数据集上的RE值均下降,如图6(c)~(f)、图7(c)~(f)所示.当ε=0.2时,键值为top40时,HISKV算法的精度相对于PCKV-GRR算法,在LNR数据集上达到了近5倍,在GAUSS数据集上达到了近6倍,其主要原因是HISKV算法利用直方图将键-值对看成一个整体进行扰动,不但减少了隐私预算分割和扰动次数,同时其增大了扰动成真实数据的概率. 针对本地差分隐私保护下收集键-值数据存在的问题,本文结合现有的该类数据收集算法存在的不足,提出了基于直方图技术的收集算法HISKV,引入基于用户分组策略的最优截断长度估计算法,结合真实键的实际扰动情况设置合理的扰动概率,并利用填充-抽样技术减少用户与收集者之间的通信代价.从本地差分隐私定义角度分析了HISKV满足ε-本地差分隐私.理论分析了HISKV的无偏性、所产生的方差以及最大偏差,最后通过4种数据集验证了HISKV算法的可用性.实验结果表明,HISKV明显优于现有的同类算法.未来工作考虑动态环境下的隐私键-值数据的收集与分析问题.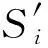
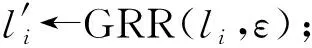
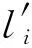
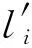
3.2 HISKV隐私性与可用性分析

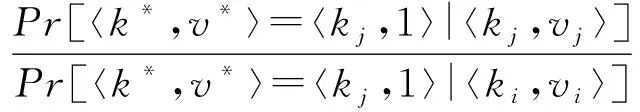
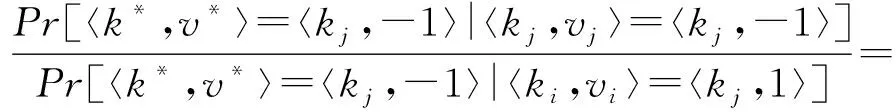
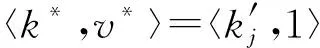


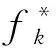

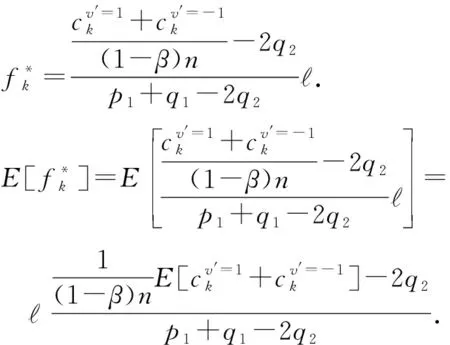
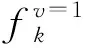
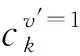
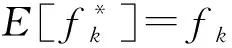
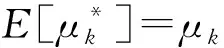

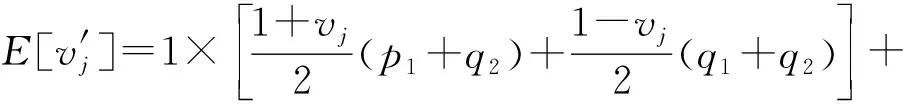
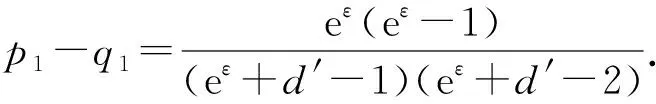
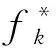
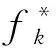
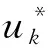
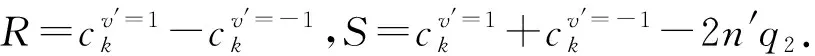
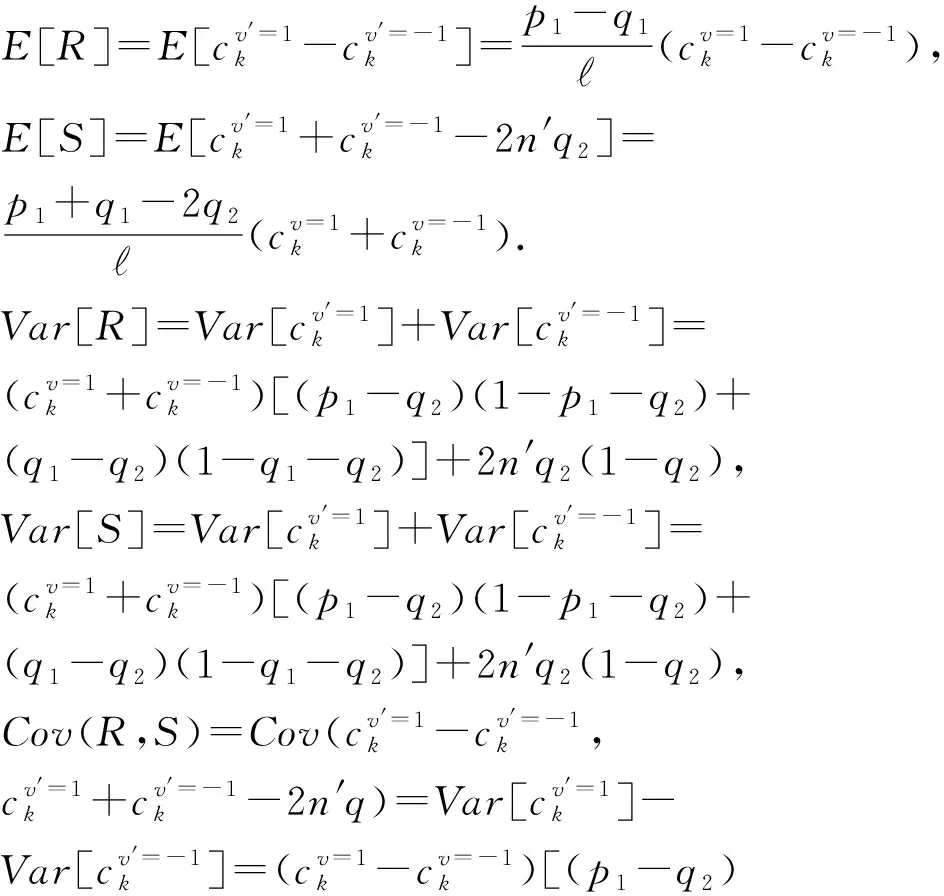
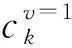
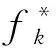
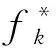
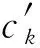
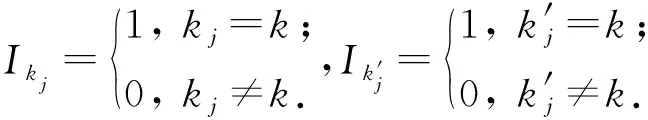






4 实验结果与分析



5 结束语
