基于维度分组降维的高维数据近似k近邻查询
2021-04-01胡晏铭郝晓红张丽平郝忠孝
李 松 胡晏铭 郝晓红 张丽平 郝忠孝
(哈尔滨理工大学计算机科学与技术学院 哈尔滨 150080)
(lisongbeifen@163.com)
随着计算机技术以及传感器技术的不断发展,基于位置的服务得到了广泛的应用,其中最近邻查询作为基于位置服务中重要的支持性技术之一,在许多领域都有广泛的应用.目前国内外学者针对最近邻查询问题进行了广泛研究,为了更好地解决现实问题,学者们提出了一系列的变形,例如概率最近邻查询[1]、反向最近邻查询[2]、连续最近邻查询[3]、组最近邻查询[4]、强邻近对查询[5]、k近邻(knearest neighbor,kNN)查询[6-7]、反向k近邻查询[8]等,其中k近邻查询问题一直吸引学者们的目光.
kNN查询问题作为最近邻查询问题的扩展形式,在现实生活中具有广泛的应用.例如送餐员在接单时会选择距离他最近的k个订单;外出旅行时游客通过手机地图查找最近的k个酒店;新闻网站通过分析与某用户最相似的k个用户的浏览历史为该客户进行新闻推荐等.kNN查询技术除了被应用在现实生活中,也被广泛应用到了科研等领域,然而与多数现实生活中处理的低维数据相反,科研领域要处理的数据多为高维数据.例如天文学中,在宇宙环境中查找与地球最相似的k个星球,不仅要考虑大小、温度,还需要考虑自转速度、大气组成成分等众多维度数据;在计算机的模式识别领域对图像进行基于kNN分类时,需要处理的图像数据的维度可高达成千上万维.由于数据维度的增长,低维空间中的kNN查询算法的效率随之下降,甚至不如线性扫描,因此学者们提出了近似k近邻(approximateknearest neighbor, AkNN)查询,通过损失一定的精度来提升查询效率,并给出一系列算法.
虽然现有的方法能够解决AkNN查询问题,但是在进行查询的过程中大多不考虑数据维度间的关联关系,对数据的所有维度进行统一的分析计算,影响了查询的准确率和效率.以基于局部敏感哈希(locality sensitive hashing, LSH)的算法为例,应用m个Hash函数对大小为n的d维数据集进行索引时,计算数据集的索引值的时间复杂度为O(dnm),可以看出其时间复杂度与维度成正相关.因此,为了提高查询的效率,本文提出了一种基于维度间的关联关系进行维度分组并降维的AkNN查询的算法.
本文主要贡献有3个方面:
1) 针对已有的高维数据近似k近邻查询算法不考虑数据维度值分布情况,面对0值维度个数远大于非0值维度个数的数据空间、查询效率降低、运算性能浪费等问题,提出了一种基于维度间关联规则进行分组降维的思想,并设计了基于LSH的维度分组降维算法,降低了维度值分布对查询的影响,提高了运算性能.
2) 针对基于维度间关联规则的维度分组降维过程中维度间关联规则挖掘效率低、挖掘关联的频繁维度耗时高的问题,本文基于单向频繁模式树提出了一个新的频繁项集挖掘算法,通过该算法能快速挖掘出频繁维度,实现维度间的关联规则高效挖掘,为高维数据的维度分组降维提供支持.
3) 针对传统的LSH编码方式查询高维数据近似k近邻存在汉明距离准确率低、Hash函数内存消耗大等问题,本文提出了基于信息熵对编码函数进行筛选和动态权重赋值,并通过加权汉明距离返回结果集的高维数据近似k近邻查询算法,提高了查询性能和效率.
1 相关工作
在低维空间下,针对kNN查询问题,研究者们提出一系列的查询方法.文献[9]针对大数据下查找k近邻效率低的问题,提出了一种基于最优三角不等式检测策略的精确k近邻快速搜索方法.在低维障碍空间中,文献[10]基于Voronoi图提出了解决障碍空间组反k近邻查询算法OGRkNN,利用Voronoi图的特性,过滤掉大量的非候选数据,有效地解决了静态障碍物环境和动态障碍物环境下的组反k近邻问题.针对障碍空间下连续反向k近邻查询问题,文献[11]根据数据点到查询区间的最大距离和数据点到障碍物的最小外包矩形的最小距离的关系对障碍物进行剪枝,同时应用R-tree对保留的障碍物进行索引,最后进行精炼和数据更新,得到最终结果.在低维路网环境中,文献[12]提出了一个平衡的搜索树索引结构G-tree,基于该索引结构解决了路网环境下的k近邻查询问题.文献[13]对时变路网环境下的k近邻查询问题进行了研究,提出了基于Voronoi图的二级索引树结构——V-tree,该文献根据时间找出了边界点作为Voronoi图的边,然后结合G-tree对Voronoi区进行索引,通过遍历树结构得到最终结果.
以上研究主要是处理低维空间环境下的k近邻查询问题及其变种,但随着维度的增长,算法查询效率随之下降.以R-tree索引结构为例,当数据维度大于20时,查询效率不如线性扫描,因此如何高效高质量地解决高维空间近似k近邻查询问题是目前研究的重点.
文献[14]为每个维度分配1个素数作为底数,每个维度上的值作为指数进行计算,并通过取对数的方式避免维度增长导致计算结果过大的缺陷,最终通过将计算结果求和的方式将高维数据降维到1维.针对高维大数据环境下绝大多数索引结构规模较大、内存不足以存储的问题,文献[15]基于Hilbert空间填充曲线和B+-tree设计了新的数据结构RDB-tree(reference distance B+-tree),同时基于RDB-tree提出了HD-index(high dimensional-index),基于该索引能够以较高的时空效率和准确率进行AkNN查询,但是存在空间填充曲线的并行通信的控制较为复杂、实现难度大的问题.文献[16]提出了基于RP-forests(random projection forests)进行k近邻查询的算法,该算法不仅适用于低维空间,还适用于高维空间,但是RP-tree(random projection-tree)的分裂次数和划分左右节点的阈值难以选择,多个RP-tree也会占用大量的空间.针对动态的大规模的二进制数据集,文献[17]提出了HWT(Hanmming weight trees)索引结构,该索引利用二进制码及其子串的汉明权值来划分二进制字符串的特征空间,进而基于HWT进行AkNN查询.针对算法参数固定导致查询的高延迟问题,文献[18]通过建立和训练梯度增强决策树模型来学习和预测何时停止查询,使算法在保持高精确度的前提下降低延迟,但是针对不同的数据集需要重复学习.文献[19]提出了基于HNSW(hierarchical navigable small world)索引结构的AkNN查询算法,该算法完全基于图,从而避免了近邻图的粗搜索阶段所需的额外的搜索结构,同时使用启发式来选择近邻图的邻居以使提高查询性能.
针对以上算法实现难度大和结构复杂的问题,Piotr Indyk提出的LSH被广泛应用于高维空间下近似k近邻查询问题.针对原始LSH根据数据集直接划分Hash桶导致查询准确率低的问题,文献[20]采用基于查询点的Hash值为基准进行桶的划分的方法,减小了与查询点相邻的数据点被划分到相邻桶的概率,提高了查询结果的准确率.文献[21]结合了基于汉明距离检索方法速度快的优势和基于查找表检索方法的结果准确的优势,提出了KMH(kmeans hashing)算法,该算法不仅提高了查询的准确率,同时也提高了查询速度.针对现有的通过机器学习的方式获得Hash函数的算法的相似指标过于粗糙的问题,文献[22]提出了一种新的细粒度相似度指标量化距离,提供了项之间相似度的更多信息,并提出基于该量化距离的查询算法,查询性能得到明显提升.文献[23]提出了冲突计数算法结构,应用欧氏空间中常用的基于2-范数的局部敏感Hash函数进行索引,算法能够很好地处理大数据环境下的高维空间近似k近邻查询.针对IO性能瓶颈的问题,文献[24]提出的O2LSH(optimal order LSH)算法将空间填充曲线作为复合Hash键值并建立线序排序,使邻近候选点更多地分布在相同或相邻的磁盘,进而提高IO性能和准确率,但是也面临着填充曲线难以实现的问题.文献[25]在索引阶段将数据对象映射到多个2维投影空间,并在每个2维空间构造一组B+-tree进行索引,有效地降低了IO开销.针对LSH无法为候选点提供准确的距离估计,导致在检查不必要的点时产生额外的计算开销从而降低了查询处理性能的问题,文献[26]提出的PMLSH(pivotiny M-tree LSH)查询框架通过建立可调的置信区间实现精确的距离估计,实现对候选集的缩减,降低了额外的计算开销.
目前现有的高维数据近似最近邻查询算法都是预先将原始数据集进行处理,然后建立索引结构,根据索引进行AkNN查询.对原始高维数据的预处理过程中,大多不考虑维度间的关联关系对查询效率和准确率的影响.因此,本文提出了基于维度间的关联规则进行维度分组的高维数据降维方法,应用该方法对高维数据进行预处理后,采用二进制编码的方式进行查询,同时基于信息熵筛选编码函数、权重的动态设定等方式优化查询方法.
2 主要定义
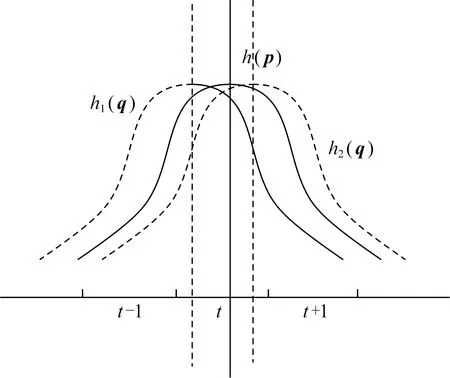
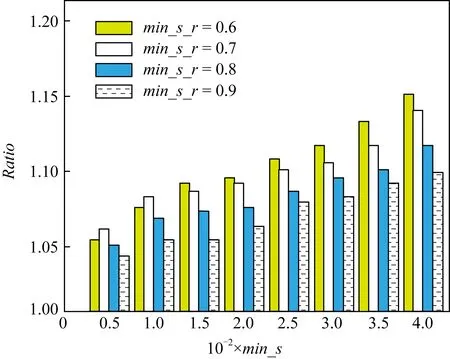
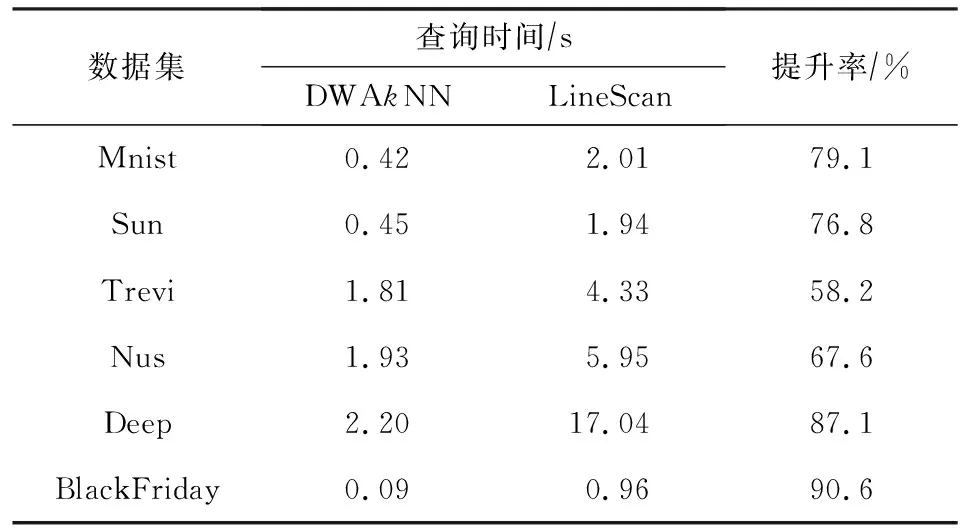
定义1.频繁序列.设temp1 在频繁项集挖掘的过程中,通过UFP-tree[27]找出所有的频繁序列就可得到所有的频繁项集,本文中如不特殊声明,频繁项集和频繁序列等价. 定义2.近似k近邻.设d维数据集X={x1,x2,…,xm},其中xi∈Rd,X经过降维和编码后得到数据集X′,对于给定查询点q∈Rd,经过相同的降维方式和编码后为q′,近似k近邻查询AkNN(q)返回1个数据集合P={p1,p2,…,pk},其中pi∈X′,数据集合P中的数据满足的条件为 定义3.局部敏感Hash函数[28].给定距离r和近似比率c,若一个Hash函数族H={h:Rd→Rd′}对给定的任意2个数据q,p满足2个条件: 1) 若dist(q,p)≤r,则Pr[h(q)=h(p)]≥P1; 2) 若dist(q,p)≥cr,则Pr[h(q)=h(p)]≤P2; 则称H是(r,cr,P1,P2)-敏感的,其中c>1,P1>P2,P1和P2是概率. 定义4.信息熵[29].信息熵是一种用于度量系统不确定性的度量方法,其香农计算公式为 (1) 其中,E(x)表示的是随机变量x的熵,x∈{a1,a2,…,an},p(ai)表示取值为ai的概率. 在高维数据中,由于维度的激增,对查询时效影响越来越大.本文通过算法1和算法2首先对数据维度之间的关联规则进行挖掘,并通过算法3对前件具有交集的强正相关的维度集进行分组;进一步根据每组的维度分配Hash函数,算法4将数据维度按组进行Hash降维;最后将降维后得到的数据应用候选的局部敏感Hash函数进行编码,算法5根据编码后的各Hash函数的熵值筛选得到编码函数和数据的编码结果.进行查询时,将查询点按相同的方式进行维度分组降维,并用相同的编码函数进行编码,然后根据编码后的汉明距离返回候选集,计算候选集中各编码位的熵值并根据熵值进行动态加权,最终算法6返回加权汉明距离最小的k个数据作为结果.整个过程可以分为基于维度分组的Hash降维、基于Hash编码的动态加权近似k近邻查询2个部分. 3.1.1 基于维度间关联规则的维度分组 本节基于UFP-tree提出了新的频繁项集挖掘算法MFIA_UFP_tree和维度分组算法Group_PAR.算法MFIA_UFP_tree通过逻辑“与”运算高效地挖掘出所有的频繁项集.算法Group_PAR基于相关系数对得到的频繁项集进行正相关关联规则(positive association rule, PAR)挖掘,进一步根据不同关联规则的前件是否有交集进行维度的分组.为了支持算法MFIA_UFP_tree和提高频繁项集挖掘效率,本节给出结构体Struct_info定义. 定义5.结构体Struct_info. Struct_info{ seq;*项转换后的序号* count;*频繁度计数* r_code;*包含序号seq的路径编码* }, 其中路径编码根据起始节点的位置来定,本文采用从0开始,从左到右依次加1的方式进行编码. 在进行基于支持度和置信度[30]的频繁项集挖掘时,首先对给定d维数据集Q={q|q∈Rd}进行二值化,对应维度有值的用“1”标记,没有值的用“0”标记,得到二值化后的数据集Q′;然后扫描二值化后的数据集Q′,去除支持度小于给定阀值的维度,对剩余维度建立序号-项集转换表,并构建UFP-tree.针对频繁项集挖掘过程中统计支持度和项集剪枝的资源消耗问题,本文根据结构体的定义,进一步给出结构体数组的定义. 定义6.结构体数组S[].给定一个UFP-tree,设结构体数组S[],当且仅当其满足的条件为: 1) 对于任意以序号i为起点、根节点为终点的路径,其序号集为Seq={seq1,seq2,…,seql},其中l为数组S[]的长度; 2)S[j].count的值为S[j].seq对应的节点在从i到根节点的路径上的频繁度计数和; 3)S[j].r_code的编码位数为从i到根节点所有路径的个数; 4)S[j].r_code的每位编码上的值为S[j].seq对应节点在该路径上的频繁度计数; 称S[]为序号i对应的结构体数组. 为保证所有的频繁序列都能根据序号对应的结构体数组挖掘得到,本文根据结构数组和UFP-tree给出定理1. 定理1.给定UFP-tree,设序列FSeq={seq1,seq2,…,seqi},若FSeq是频繁序列,则序列FSeq一定属于序号seqi对应的结构体数组S[]. 证明. 定理1可以通过反证法进行证明.假设以序号seqi为结尾的频繁序列FSeq不属于seqi对应的结构体数组S[],由UFP-tree的结构可知,任意以seqi为结尾的频繁序列一定属于以序号seqi对应的节点为起点、根节点为终点的1条或多条路径,根据结构体数组的定义可知,任意1条从序号seqi对应的节点到根节点的路径都是序号seqi对应的结构体数组的子集,所以序列FSeq也属于序号seqi对应的结构体数组,与假设矛盾. 证毕. 在进行基于UFP-tree频繁项集挖掘时,根据结构体数组S[]来进行以序号i为终止端点的频繁序列挖掘,进而得到对应的频繁项集.因此根据结构数组S[],进一步给出定理2~4. 定理2.在序号i对应的结构体数组S[]中,若S[t].count小于最小支持度计数countmin,则以序号i为终止端点的所有频繁序列一定不包含序号S[t].seq. 证明. 以反证法进行证明.假设S[t].count 证毕. 推论1.若有序序列{temp1,temp2,…,tempj}不是频繁序列,则该序列的超集也不是频繁序列. 定理3.在UFP-tree上,从序号i对应的树节点到树根的路径频繁度计数等于该路径上序号i的频繁度计数. 证明. 根据UFP-tree构建的过程和定义,显然每条子树的叶节点的频繁度计数小于等于其父节点的频繁度计数,从序号i对应的树节点到树根的路径可以看成以序号i对应的树节点为叶节点的子树,在这棵子树中,显然序号i的频繁度计数最小,所以该子树的频繁度计数为序号i的频繁度计数,所以定理3得证. 证毕. 应用定理3可快速得到每条路径的频繁度计数. 定理4.设序列{temp1,temp2,…,tempj}是以序号tempj为终止序号的序列,当且仅当序列对应数组节点中的编码进行“与”运算的结果C中各位的和不小于最小支持度计数时,该序列为频繁序列. C=S[t1].r_code&…&S[tj].r_code, (2) 其中,ti为序号tempi在数组S[]中对应的下标. 证明. 根据结构体Struct_info的定义可知,路径编码r_code为序号seq在各路径上频繁度计数的分配情况,当序列中的某些序号出现在同一条路径下时,这些序号在该路径对应的编码位的数值相同,未在同一条路径的其余序号在该路路径对应的编码位的数值为0.即结构体数组中任意2个元素的路径编码进行“&”运算的结果可根据式(3)获得: (3) 其中,r_codeit表示结构体数组中下标为i元素对应的路径编码第t位的值,ct表示C的第t位数值.由于各序号对应的编码位进行“与”运算得到的结果为序列中各序号共同出现在各路径下的情况,结果各位数值进行求和计算,结果为序列的频繁度计数. 证毕. 进一步给出频繁项集挖掘算法MFIA_UFP_tree,如算法1所示,首先倒序遍历序号,得到每个序号对应的结构体数组,然后调用算法2(MiningFS)进行频繁项集的挖掘. 算法1.MFIA_UFP_tree(UFP_tree,countmin). 输入:UFP_tree为UFP-tree、最小支持度计数countmin; 输出:所有频繁项集FP. ①S[]←∅,FP←∅;*初始化结构体数组S[]和频繁项集FP* ② fori=max_ordertoldo ③ 将i的指针赋值给临时变量Tp和tp; ④ while (Tp≠NULL) ⑤j←0; ⑥ if (!S.contain(tp)) then ⑦j←j+1; ⑧ 将tp指向的序号的结构体添加到结构体数组S[]; ⑨ else then ⑩S[tmp].count←S[tmp].count+tp.count;*tmp为序号tp在结构体数组S[]内的下标* 算法1倒序遍历序号,求得以每个序号为起点、根节点为终点的所有路径的结构体数组(行②~),首先遍历每条路径上的节点(行③,行~),进一步判断数组中是否含有该节点,当不含时,将节点添加到S[]中,并将S[]的长度j加1(行⑦~⑨),否则找到该节点在S[]中的位置,更新结构体信息(行~),获得对应的结构体数组S[]后,调用算法2对每条路径进行频繁项集的挖掘(行).算法2如下: 算法2.MiningFS(S[],j). 输入:结构体数组S[]、数组长度j; 输出:频繁项集FP. ①Length←j; ②FP←FP∪{S[0].seq}; ③NFP[]←∅;*记录所有长度为2的非频繁序列的第2个序号* ④ fori=0 tojdo ⑤ if(S[i].count ⑥ 删除S[i]; ⑦Length←Length-1; ⑧ end if ⑨ end for ⑩ forF_len=2 toLength+1 then 算法2根据结构体数组S[]进行频繁序列挖掘,首先记录所有长度为2的非频繁序列(行③),应用定理2进行剪枝(行④~⑨),进一步根据剪枝后的频繁序列候选集的长度进行频繁序列的挖掘(行⑩~). 挖掘出所有的频繁序列后,对频繁序列进行关联规则挖掘.本文基于相关系数挖掘正相关无冗余关联规则,其中相关系数计算: (4) 其中,supp()为支持度,A和B分别是要挖掘的关联规则的前件和后件. 根据关联规则的定义可知,当关联规则A→B是强关联时,说明前件A的出现对后件B的出现起到了促进作用,即有很大的可能当A出现时B也出现,因此给出定理5作为维度分组依据. 定理5.正相关关联规则A→B,若conf(A→B)=1,则前件A出现时后件B必然出现.(conf(A→B)表示关联规则A→B的置信度) 证明. 当conf(A→B)=1时,则count(A∪B)=count(A),即前件A和后件B共同出现的次数等于前件A出现的次数,即前件A出现后件B必然出现. 证毕. 通过算法1获得频繁项集后,基于相关系数进行关联规则的挖掘,并依据定理5将相关联的维度合并到1个分组,当不同关联规则的前件有交集时,相关的维度分组进行合并.进一步给出分组算法Group_PAR,如算法3所示: 算法3.Group_PAR(FP,ρmin). 输入:维度频繁项集FP、最小相关系数ρmin; 输出:维度分组情况Group. ①PAR←∅,Group←∅,j=0; Group记录分组情况* ② forX∈FPdo ③ 根据式(4)计算所有由频繁序列X生成规则的相关系数ρAB,其中A∪B=X,A∩B=∅; ④ if (ρAB≥ρmin) then ⑤ if (conf(A→B)≥1) then ⑥PAR←PAR∪{A→B}; ⑦ end if ⑧ end if ⑨ end for ⑩ forY∈PARdo*Y的格式为A→B* 算法3先遍历频繁项集,对每个项集进行关联规则的挖掘,生成关联规则(行②~⑨),然后删除冗余规则(行⑩~),对生成的正相关无冗余规则应用定理5进行分组,最终得到分组情况Group(行~). 3.1.2 基于维度分组的Hash降维 本节对维度分组后的数据集进行Hash降维,同时提出符号位的概念并给出定义.当组内维度个数大于1时,通过LSH函数进行降维,同时在新生成的维度上保持着原维度上的相对位置关系.本文采用的Hash函数是2-稳定分布LSH函数[31],其碰撞概率为 (5) 由于数据被Hash函数映射后数据位置关系发生偏移,本文对Hash降维后的数据设置了符号位,并给出符号位的定义. (6) 根据符号位的定义和2-稳定分布LSH函数的性质,进一步得出性质1,并根据性质1来筛选候选集,提高查询的准确率. 性质1.2个距离相近的数据经过相同的LSH函数映射后,落入相邻的Hash桶中的数据对应符号位相同. 设Δ=|a·q+b|%w,t=ha(q),当Δ<0.5w时,由图1可知,ha(q)的概率分布向左偏移,点q经过Hash函数映射后有较大概率落入t-1桶的右半部分,即t-1桶中符号位为|t-1|+0.5的数据中存在点q的映射结果.同理Δ≥0.5w时,t+1桶中符号位为|t+1|-0.5的数据中存在点q的映射结果. Fig. 1 Schematic diagram of sign bit identical probability图1 符号位相同概率示意图 通过算法3得到维度分组情况后,算法4首先根据分组结果中每个组中包含的项数来初始化Hash函数,随后对数据进行Hash降维,根据每个组中包含的维度个数分配Hash函数,并将每组中的维度看成1个向量并进行计算,进一步根据式(6)计算符号位数值,最终返回降维后的数据集.因此,给出维度分组后进行降维的算法Reduce_dim,如算法4所示: 算法4.Reduce_dim(w,Group,X). 输入:桶宽w、数据维度分组情况Group={g1,g2,…,gm}、原始数据集X={x1,x2,…,xn}; 输出:降维后的数据集X′. ①X′←∅; ② fori=0 tomdo ④ 为每个维度组初始化Num_func个Hash函数; ⑤ end for ⑥ fori=0 tondo ⑦ 对xi进行Hash降维; ⑩ end for 数据经过维度分组和Hash降维后,为了提高计算速度,本文将降维后的数据进行编码,即x∈{0,1}l.根据编码后的数据,应用熵理论对Hash编码函数进行筛选.本文应用2-稳定分布LSH进行编码,方法为 (7) 其中,a是服从2稳定分布的随机函数产生的一个D-|Z|维向量,D为降维后的数据维度,Z为符号位,|Z|是符号位的长度.根据信息熵和Hash编码的特性,进一步给出定理6. 定理6.若Hash函数将数据对象映射成0和1的概率越相近,那么该Hash函数的散列效果就越好. 证明. 根据式(7)对数据进行0,1编码,其中Hash函数相当于二元信源,0和1为二元信源符号,二元信源熵的计算公式为 entropy(Y)=E(Y)=-ωlgω-ϖ lg ϖ, (8) 其中,E(Y)是ω的函数,ω为信源符号概率. 根据式(8)可知,当信源符号出现的概率越接近,信息熵越大,即Hash函数编码结果越不确定,散列效果越好.因此得证. 证毕. 由于二进制编码的长度对查询准确率有着显著的影响,为提高编码质量,本文基于定理6筛选出熵值大的函数作为映射函数进行编码.数据经过算法4进行维度分组降维预处理后,应用算法5对其进行编码. 算法5.Hash_code(X′,l). 输出:编码后的数据集X_c. ①X_c←∅; ② 初始化2l个Hash编码函数;*随机变量维度为D-|Z|维* ③ fori=0 tondo ⑤ end for ⑥ fori=0 to 2ldo ⑦ 根据式(8)计算每个编码Hash函数的熵; ⑧ end for ⑨ 选择出熵为前l大的函数作为编码函数; ⑩ fori=0 tondo 算法5先随机生成2l个Hash函数,进一步根据式(7)进行Hash(行①~⑤),编码后对编码函数进行筛选,计算每个编码函数对应的熵值,选择出熵值为前l的函数作为编码函数(行⑥~⑨),最终将多余的编码删除得到最终编码数据集(行⑩~),因此时间复杂度为O(ln). 当进行查询时,将查询点q进行相同处理,通过与编码后的数据集X_c中的数据进行比较,返回汉明距离在小于给定阈值dismin的数据作为候选集CS,进一步根据性质1筛选候选集,基于候选集中的每位编码与查询点对应位的编码相同的概率,对编码位进行权重赋值,然后计算查询点q与候选集CS中数据的加权汉明距离,根据加权距离进行排序 并返回前k个数据.由二元信源熵函数可知,相同编码位的编码相同的概率越大,对应编码位的可信度就越高,权重越大.根据熵权法对第i位设定权重: (9) 其中,ei为第i位的信息熵值. 当对数据集进行编码后,输入查询点进行相同的维度分组降维以及编码后,基于加权汉明距离进行查询,同时查询过程中动态调整权值.查询算法如算法6所示: 算法6.DWAkNN(X_c,q,dismin). 输出:q的近似k近邻. ①CS←∅;*CS为候选集* ②q′←Reduce_dim(w,Group,q); ③q″←Hash_code(q′,l); ④ fori=0 tondo ⑦ end if ⑧ end for ⑨ 根据式(8)计算候选集CS中每位编码的熵;*概率为与查询点q对应编码位相同的概率* ⑩ 根据式(9)计算候选集CS中每位编码的权重; 算法6先将查询对象q进行降维并进行编码(行②③),然后遍历编码后的数据集X_c,返回汉明距离小于dismin的数据并添加到候选集CS(行④~⑧),计算候选集中数据的每位编码位的熵值,进一步根据熵值计算编码位的权重(行⑨⑩),最后计算加权汉明距离并进行升序排序,当加权汉明距离相同时,根据符号位相同的个数进行排序,最终返回前k个数据作为查询结果(行~). 为了评估算法性能,分别测试了自身参数对算法性能的影响以及与对比算法的性能. 本节实验分析关联规则最小支持度min_s、频繁项集最小支持度min_s_r和l对算法准确率的影响以及数据维度对算法查询时间的影响.准确率Ratio其值为近似k近邻距离与真实k近邻距离之比的平均数,其值越接近1说明算法查询质量越高,准确率Ratio计算方式为 (10) 本节实验使用的数据集为真实数据集和人工数据集.分别是由IBM Almaden Quest研究小组的生成器生成的数据集T40I10D100K和由Roberto Bayardo从PUMSB中提供的pumsb数据集和由Claudio Lucchese等人通过爬虫得到的网络文档数据集webdocs_samping.数据集是从FIMI信息库下载得到(1)http:fimi.uantwerpen.bedata.3个数据集被广泛应用于频繁项集挖掘试验.由于数据集webdocs过大,从原始数据集中随机选取10万条数据作为数据集进行实验,并对数据信息进行了适当调整和优化.该数据集记为webdocs_samping.数据集属性如表1所示: Table 1 Attribute Sheet of Experimental Data Set forParameter Analysis 在实验中,分别从各数据集随机抽取5 000条事务作为查询点进行查询,最后计算平均时间和准确率作为比较. 实验1.首先分析参数min_s和min_s_r对本文所提算法的准确性的影响.其中k=50,编码长度l=32 b,Hash函数的桶宽w=4.由于数据集T40I10D100K是一个稀疏数据集,因此分析了参数min_s从0.5%~4%变化过程中对算法准确率的影响;数据集pumsb和webdocs_sampling相对稠密,因此分析了参数min_s从60%~95%的变化过程对算法正确率的影响,同时参数min_s_r的取值为60%,70%,80%,90%.参数影响分别如图2~4所示. Fig. 2 Experimental result on dataset T40I10D100K图2 在数据集T40I10D100K上实验结果 Fig. 3 Experimental result on dataset pumsb图3 在数据集pumsb上实验结果 Fig. 4 Experimental result on dataset webdocs_sampling图4 在数据集webdocs_sampling上实验结果 通过图2~4可知,在3个数据集上当min_s_r固定时,Ratio随着min_s的增大呈现上升的趋势,由Ratio的计算公式可知,当Ratio偏离1越远,算法的查询结果的准确性越低,因此当min_s_r的值固定时,算法在3个数据集上的查询准确性随min_s的增大而降低.这是由于当min_s_r固定时,随着频繁项集最小支持度min_s的增大,导致在进行分组降维的过程中忽略的项增多,致使降维后的误差大.同时在3个数据集上当min_s固定时,Ratio总体上随min_s_r的增大而更趋近于1,即算法的准确性随min_s_r的增大而增大,这是由于在分组降维过程中,关联规则的质量影响着维度的分组,min_s_r越大说明关联规则的前后件关系越紧密,组内的非零值维度越多,减少了Hash函数中随机变量的维度和Hash函数的个数,降低了降维后的误差. 实验2.分析参数l对查询准确率的影响.在本实验中,设在数据集T40I10D100K中min_s=2%,另外2个数据集中为75%,设min_s_r在3个数据集中都为90%,k和w分别为50和4,分析l的值为8,16,32,48,64对查询准确率的影响,结果如图5所示: Fig. 5 Effect of l on Ratio图5 l对Ratio的影响 由图5可知,在3个数据集上Ratio都随着编码长度l的增大而更趋近于1,即算法的查询准确性随着l的增大而增大,当编码位数大于32 b时,编码位数对查询结果的提升幅度变小,这是由于算法在将数据从欧氏空间映射到汉明空间时本身信息缺失导致的. 通过实验1和实验2可以看出,本算法能以较高的正确率返回k近邻,在稀疏和稠密数据集上表现都比较优异. 本节通过与对比算法比较不同k下查询结果的准确率和查询时间进一步评估本文算法性能. 1) 数据集.本节应用真实数据进行对比实验,所用的数据集分别是Mnist,Sun,Trevi,Nus,Deep,BlackFriday.其中前5个数据集通过GitHub网站获取(2)https:github.comDBWangGroupUNSWnns_benchmark,被广泛应用于现有的AkNN查询实验.原始BlackFriday数据集是从Kaggle平台(全球数据科学竞赛在线平台)获取(3)https:www.kaggle.comsdolezelblack-friday,由于原始数据集包含不相关的属性,因此对其进行了数据清洗,只保留了每个用户的购物信息.数据集属性如表2所示.在查询时,我们从每个数据集中随机选取500个数据点作为查询点,每个查询点重复查询50次,k分别取值为10,30,50,70,90,默认k=50,取查询时间和查询准确率的平均值作为算法的性能指标. 2) 对比算法.我们选择HD-Index查询算法[15]、HWT查询算法[17]和QALSH(query-aware LSH)查询算法[20]与本文所提出的DWAkNN查询算法进行对比.所选算法分别基于Hilbert空间填充曲线、汉明加权树和LSH实现. Table 2 Comparison the Experimental Data Sets表2 对比实验数据集 3) 参数设置.本文算法的参数min_s,min_s_r,w分别设置为0.04,0.9,4,编码长度l=32 b.根据文献[15]的实验结果,将算法HD-Index的参数m,τHD-Index,α,βHD-Index分别设置为10,16(在数据集Trevi和BlackFriday上值分别设为64和60)、4 096和4 096,其中m为参考点个数,τHD-Index为RDB-tree的个数,α为经过RDB-tree剪枝获得候选集个数,βHD-Index为经过三角不等式进行进一步过滤的候选集个数.根据文献[17]的实验过程,算法HWT的参数τHWT设为1 000,同样应用LSH将数据集的实值向量映射到二进制码,在本文中设置二进制长度为32 b. Fig. 6 Influence of k on query time图6 k值对查询时间的影响 首先测试k值对查询时间的影响.实验结果如图6所示.由图6可以看出4个测试算法在6个数据集上的查询时间都是随着k的增大呈上升趋势,本文算法效率优于算法QALSH和HD-Index,当k=50时,查询效率分别提高了25.0%~72.8%和20.0%~63.0%.但是查询时间略高于算法HWT.这是由于本文算法在进行查询时会动态设置编码位的权重,然后进行加权排序,导致查询时间略高于算法HWT.根据图6(b)(d)可以看出,随着数据规模的增大(Sun数据集和Nus数据集维度相差不大,规模相差1个数量级),4个算法的查询时间也都增大. Fig. 7 Influence of k on Ratio图7 k值对Ratio的影响 其次测试k值对查询准确率的影响.实验结果如图7所示.由图7可以看出除了在数据集Black-Friday,算法QALSH的Ratio接近1,查询质量最高,算法DWAkNN次之,算法HD-Index和算法HWT相差不大,略高于算法DWAkNN,在数据集BlackFriday上,算法DWAkNN最优.这是由于算法DWAkNN通过对维度间的关联规则进行分组降维后再进行编码,减少了数据信息的丢失,然而除购物信息数据集BlackFriday外,其他数据集都是图像类型,数据维度间的关联性不稳定,维度分组降维对算法的查询准确率提升小于在BlackFriday数据集上的提升,因此在表2的前5个数据集上的查询质量略低于QALSH算法,但是与同样应用LSH对数据进行编码的HWT算法相比,算法DWAkNN的查询质量更优.同时结合图6的查询时间结果图可以看出,在相同数据集上,本文所提算法DWAkNN能够以较低的查询时间返回更接近真实k近邻的近似结果,算法的综合性能更优. 最后测试本文算法与线性扫描(LineScan)查询算法在高维数据集下的性能对比(高维空间线性扫描算法效率高于低维查询算法).实验结果如表3所示,可以看出本文算法的效率远高于LineScan算法. Table 3 High-Dimensional Data Set Query Time and Efficiency Improvement Table 通过实验可得,本文所提算法DWAkNN能够以较低查询时间返回较高质量的AkNN查询结果,与目前先进AkNN查询算法相比,综合性能更为优越,尤其提高了维度间关联关系明显的数据集下AkNN查询的准确率,同时与传统的低维空间下的查询算法相比较,算法DWAkNN在高维空间下的查询效率得到大幅度的提升. 本文对高维空间下近似k近邻查询问题进行了研究,针对高维数据降维过程不考虑维度间的关联关系的问题,提出基于关联规则的维度分组降维算法Reduce_dim,进一步提出了Hash_code算法,该算法基于LSH对降维后的数据进行编码,并应用信息熵理论筛选编码函数,最终提出了动态加权汉明距离近似k近邻查询算法DWAkNN,算法应用符号位对候选集进行筛选,提高了查询准确率.实验结果表明,本文提出的算法具有较好的性能.未来研究重点主要集中在基于神经网络的高维空间近似k近邻查询问题等方面.3 高维数据近似k近邻查询
3.1 基于维度分组的Hash降维
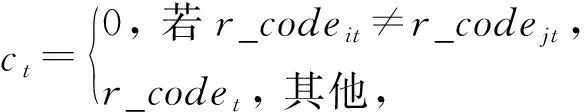
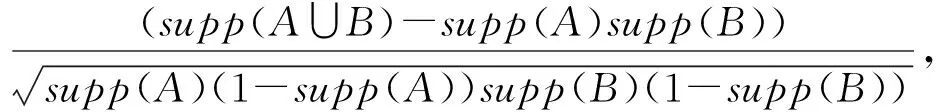
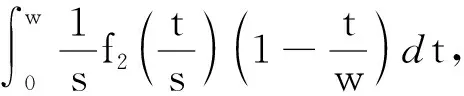




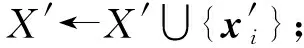
3.2 基于动态加权的近似k近邻查询

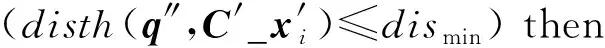
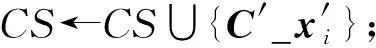
4 实验分析
4.1 参数分析



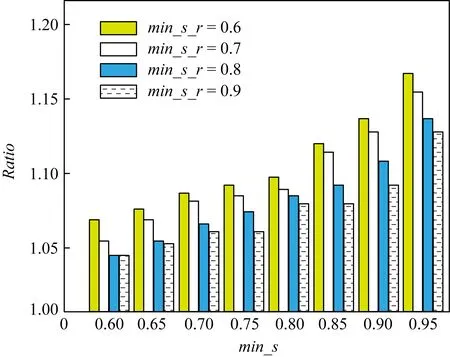

4.2 算法对比


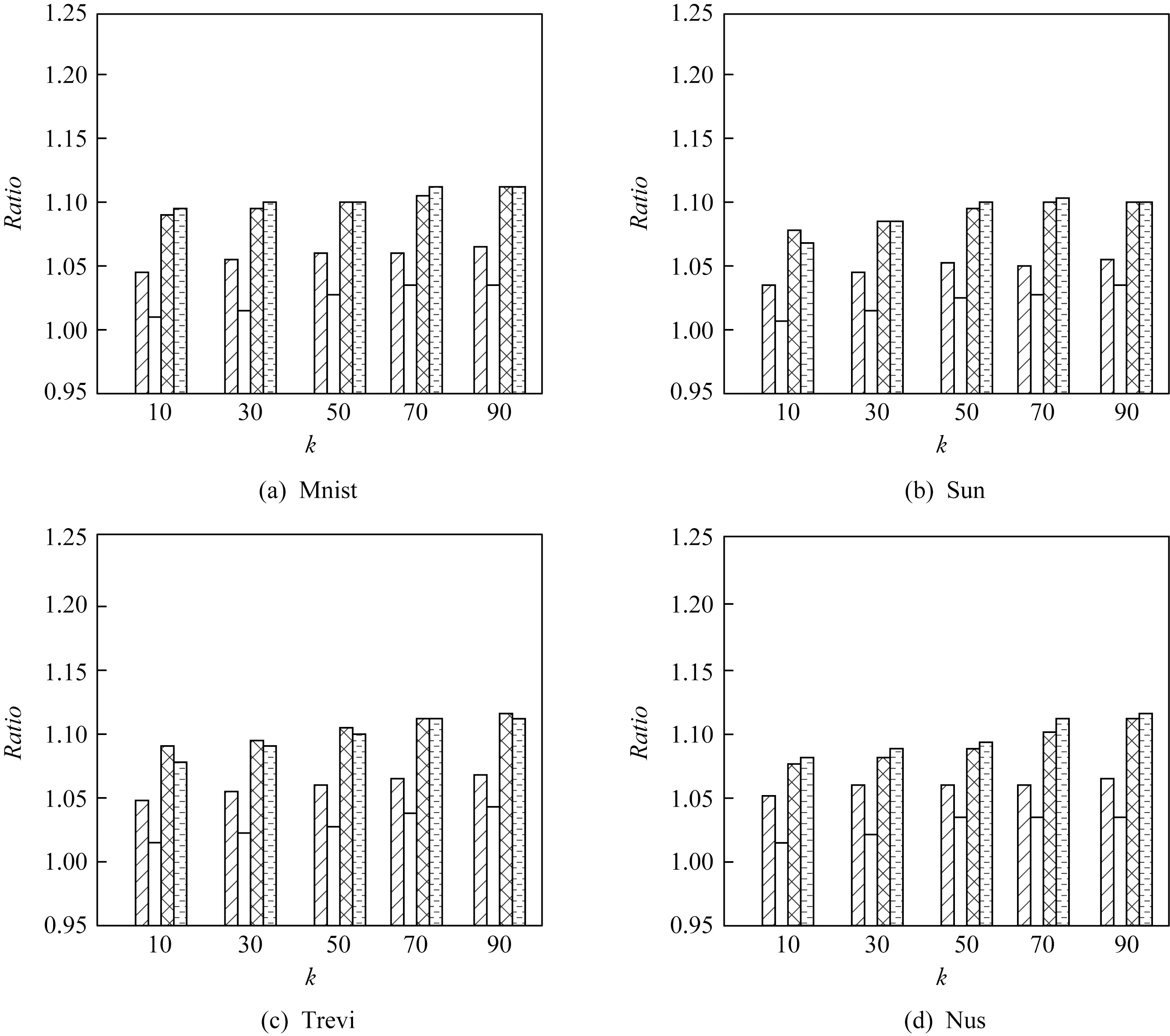
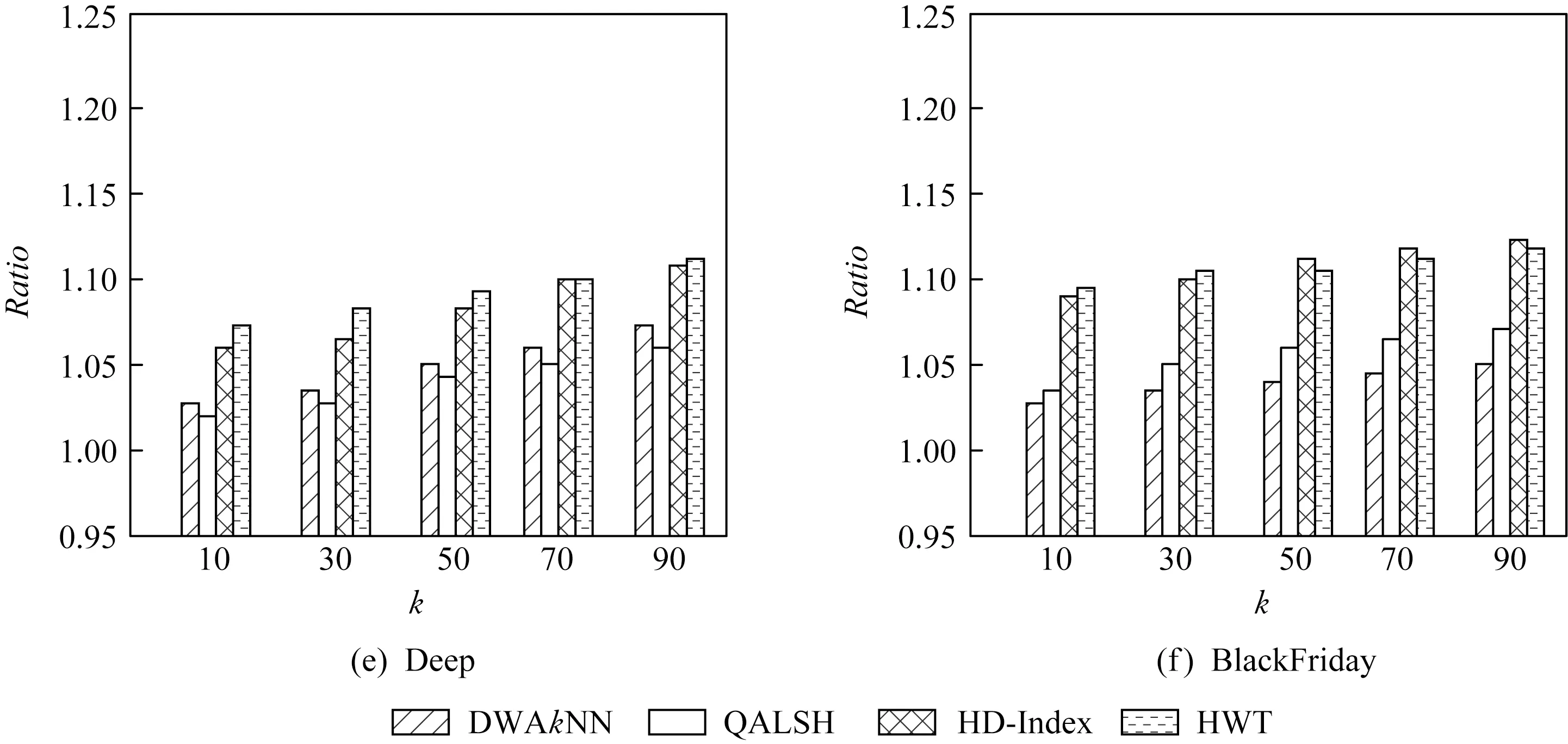
5 总 结
