复杂环境下果园机器人路径规划方法研究*

杨保海，任全会，李海生

(1. 广西民族师范学院数理与电子信息工程学院，广西崇左，532200； 2. 河南省智慧教育与智能技术应用工程技术研究中心，郑州市，451460)

0 引言

目前，水果生产在农业经济中占有非常重要的地位，和其它农业产业相比果园生产机械化程度比较低，果园的生产管理还主要靠人工完成[1]。主要是因为果树不但树冠较大，而且冠层还低，因此普通的农机很难进行具体的操作。人工操作的成本高，水果的价格不稳定等问题都会影响果农的积极性。随着人工智能、物联网以及自动化技术的快速发展，果园机器人也得到了广泛的应用，这样就可以大大提高生产效率，同时还降低了种植果树的成本[2]。

果园机器人热点和重要的问题就是路径规划，也就是在果园这个复杂的环境下能够很好地寻找从起点到目标点的无碰撞移动路径[3]。国内外的学者针对路径规划的问题进行了大量的研究，目前研究路径规划的算法有很多，比如有学者提出的人工势场算法，这种算法具有数学模型简单、计算量小、易于实现的优点，不过该算法应用到环境复杂的果园中就会造成锁死的现象，而且迭代次数大大增加；还有学者提出了蚁群算法，此种算法的平均角度偏差较大，而且需要更多的迭代次数；其它算法的还有粒子群算法以及神经网络算法等等，此类算法如果应用到果园机器人上会出现参数不确定以及计算量大等诸多问题[4]。

为实现复杂环境下果园机器人路径规划，本文提出了一种新的方法，也就是在基本人工势场算法的基础上进行优化[5]。引入使用了障碍物检测算法，此算法剔除了果园机器人的斥力作用，引入一个障碍物有关的边界条件参数，这样不但避免了死锁现象，还消除斥力的影响从而得到更优的移动路径。

1 基本人工势场算法

人工势场算法由美国斯坦福大学教授Khatib提出的[6]。假设果园机器人的初始位置是S=[xy]，终点位置是SE=[xeye]。引力势场函数可以表示成

(1)

式中:br——力场的增益系数，并且其值是正数。

假设引力势场函数的负梯度[7]可表示成

(2)

式中:φ1——果园机器人起始点之间的距离，φ1=‖S-SE‖；

β1——单位向量。

通过式(1)和式(2)可以看出，引力和初始点的距离的关系是线性的[8]，因此就可以把障碍物产生的斥力场函数表示出来。

(3)

式中:φ——果园机器人到障碍物最短距离；

φ0——障碍物影响的长度；

b0——增益系数，并且其值是正数。

通过式(3)可以看出，参数φ0受障碍物斥力影响比较大，但是，如果不在这个方位内，则其斥力不再影响此参数。此时的斥力场函数的负梯度就可以表示成

(4)

果园机器人受的合力就可以表示成

F(S)=FH(S)+F0(S)

(5)

通过式(1)～式(5)可以看出，果园机器人路径规划和避障的时候缺点非常的明显，主要表现在三个方面：其一，如果出现障碍物的斥力相加之后和引力的值一样，并且相位相反，此时会出现死锁现象；其二，因为斥力的存在，会出现无法到达终点的情况；其三，在复杂环境下，计算效率会大大下降，同时需要更多的迭代次数[9]。

2 算法改进

基于对人工势场算法原理和其存在的问题的分析，主要从两个方面进行改进，首先使用障碍物检测算法识别路径，引入边界条件这个参数，降低障碍物的受力影响[10]。

2.1 重构识别路径

路径重构主要使用障碍物检测算法实现，此算法的核心就是计算出一个科学的路径中间点[11]。

假设果园机器人的初始位置是SQ=[xqyq]，终点位置是SD=[xdyd]，因此起始点的直线∑z的方程可以表示成

(6)

式中:round——取整函数。

仿真环境横向方格数为Mh，纵向的方格数为Mz，果园机器人的活动范围就可以设定成{(x，y)|0≤x≤Mh同时0≤y≤Mz}，方格到∑z的方程距离可以表示成

(7)

式中:m、n——仿真方格中的纵、横坐标；

B——常数，并且其取值为大的正整数。

通过对式(7)分析可以看出，l的值存在正负值两种可能。假设ψ为障碍物方格的边沿，因此就有一个点到∑z的距离是正最大值，这个点的坐标设定成Smax,δ=[xmax,δymax,δ]，同时还有一个点到∑z的距离是负最小值，这个点的坐标设定成Smin,δ=[xmin,δymin,δ]。因此，就可以把ψ周边的路径中间点坐标表示出来。

(8)

(9)

2.2 优化斥力作用

仿真环境中，果园机器人可能移动的方向有8种，所以，果园机器人在移动的时候需要承受各方向上的作用力。为了便于分析，可以通过3×3的矩阵来存储，其名称也可以称为力向矩阵[12]。

通过对基本人工势场算法的分析可知，在果园机器人移动的过程中会受到障碍物的斥力作用，因此，果园机器人在移动的时候不能实现贴近障碍物移动，这就会造成果园机器人移动路径变大。消除斥力的影响就可以得到更优的移动路径，为此，本文使用了障碍物边界条件的概念，也可以理解为障碍物对果园机器人作用力一直是0。这就可以实现果园机器人在移动的时候只受两个因素的影响，一个是终点产生的引力，另外一个就是外部环境。假设果园机器人在S位置的受力方向矩阵

(10)

式中:In m——环境约束矩阵；

*——卷积运算。

In m代表的是仿真环境中果园机器人周边方格的情况，可以把Inm表示成

(11)

(12)

如果要实现最优分解，就必须要符合

(13)

式中:j、i——行、列代号，其取值只能是{-1，0，1}；

βn m——方向向量，其取值范围是(j，i)；

τn m——分解系数[13]。

果园机器人哪个方向受力最大，其会向哪个方向移动，因此就可以把路径点的迭代表示成

S′=S+ηn m

(14)

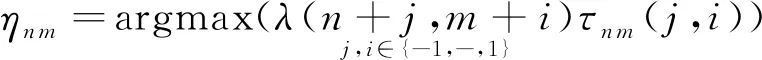
式中:ηn m——最大引力分量方向向量；

S′——下一路径点位置向量。

2.3 改进算法流程

改进算法的流程主要分为四步进行：第一步，对各个参数进行初始化包括仿真地图信息矩阵Da和搜索矩阵Db；第二步，通过障碍物检测算法找出两个参数，这两个参数是中间点与有效障碍物，与此同时将中间点作为局部路径的终点，重复这个过程，确定没有其它的有效障碍物和中间点，这样就得到了第一个有效的中间点，同时把最后一个有效障碍物方格的特点数据进行移动，也就是把此数据从Da复制到Db；第三步，通过优化斥力作用的原理检索Da的力向矩阵，接着检索出受力最大的方向，同时按此方向从起点重新检索，这样就可以得到一个局部最优路径；第四步，把终点设置为新的起点，把最终的目标点设为新的终点，按第二步和第三步重新进行检索，如果出现了最终的目标点变成了起点，就停止搜索，这样路径规划就结束了，最终的全局路径就是由各个局部最优路径组成[14]。

此算法对路径进行的重构，因为各个局部路径之间没有新的障碍物和中间点，所以就避免了基本人工势场算法中的死锁现象；因为优化了斥力作用，这样果园机器人就能够紧贴障碍物进行移动，所以就能得到更短的局部路径，进而实现最优的全局路径。

3 测试结果

为了验证本文算法的正确性，本文在复杂环境下进行了对比测试，仿真软件使用Matlab[15]。

果园机器人的移动环境使用栅格法进行构建，设定黑色栅格为障碍物，左下角为果园机器的起点，右上角为果园机器的目标点，起点坐标是(0，0)，终点的坐标是(l，h)，每一个小方格的尺寸是a×a，两个方向总的方格数可表示成

(15)

式中:Nh——纵向小方格的数量；

Nl——横向小方格的数量；

ceil——向上取整函数。

构建的环境如图1所示，测试结果如图2所示。从图2可以看出，初始状态下，两种方法路径规划相差不大，随着障碍物的增多，基本人工势场算法陷入局部最优解。本文算法用障碍物检测算法识别路径计算出一个科学的路径中间点，同时优化了斥力作用，避免了局部最优解，充分使用收敛次数构建出反馈通道，这样就可以大大减少了迭代过程中的波动性。和基本人工势场算法相比，本文算法收敛过程更加平稳。

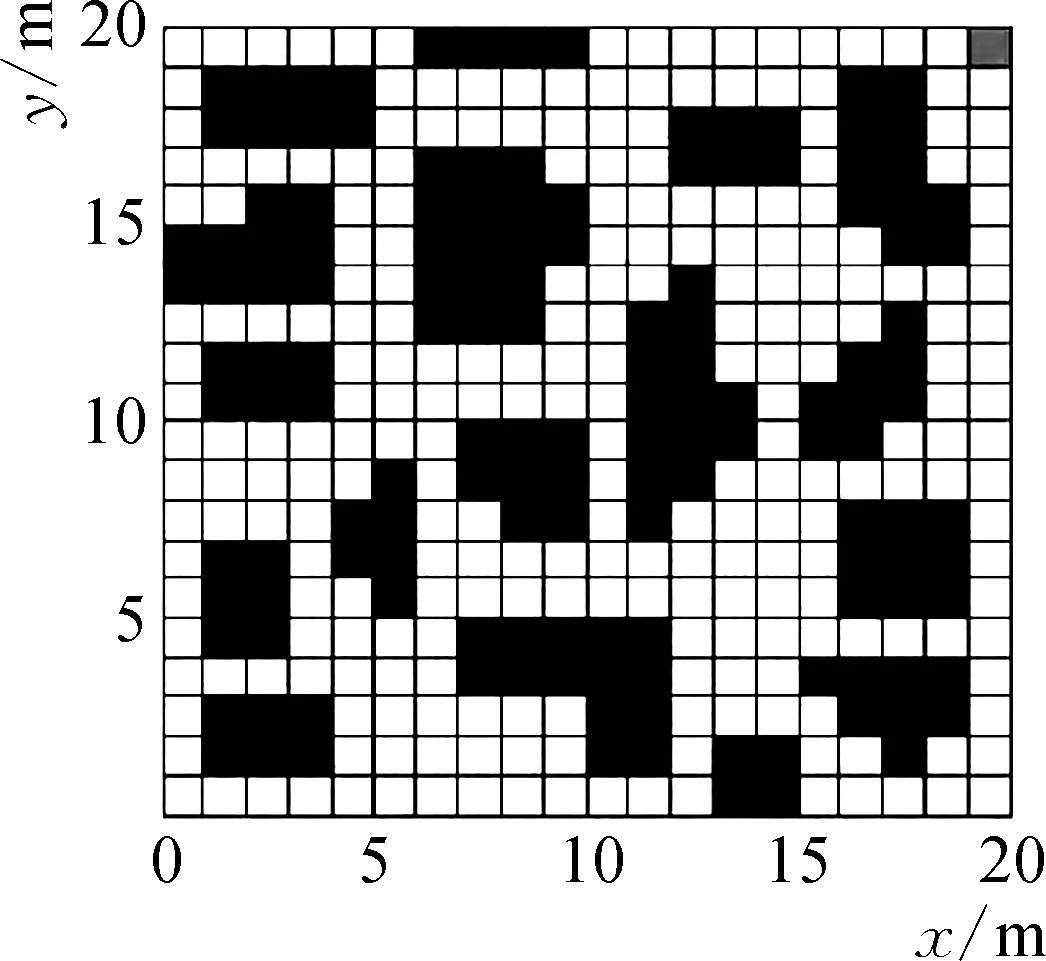
图1 仿真环境Fig. 1 simulation environment

复杂环境下路径长度迭代对比如图3所示。两种算法测试结果对比如表1所示。通过图3、表1可以看出，基本人工势场算法得到的规划路径长度为29.873 m，本文算法得到的规划路径长度为29.287 m，最优路径长度有了一定的减少；基本人工势场算法需要27次迭代才能收敛到最优路径，但本文算法收敛到最优路径仅需要8次迭代就能实现，迭代次数减少了19次，大大减少了迭代次数；基本人工势场算法运行时间12.127 s，本文算法运行时间3.465 s，运行时间减少了近9 s。基本人工势场算法波动较大，对算法的收敛速度产生不利的影响，而本文算法在迭代过程中的波动较小，收敛过程非常平稳，因此收敛速度较快。

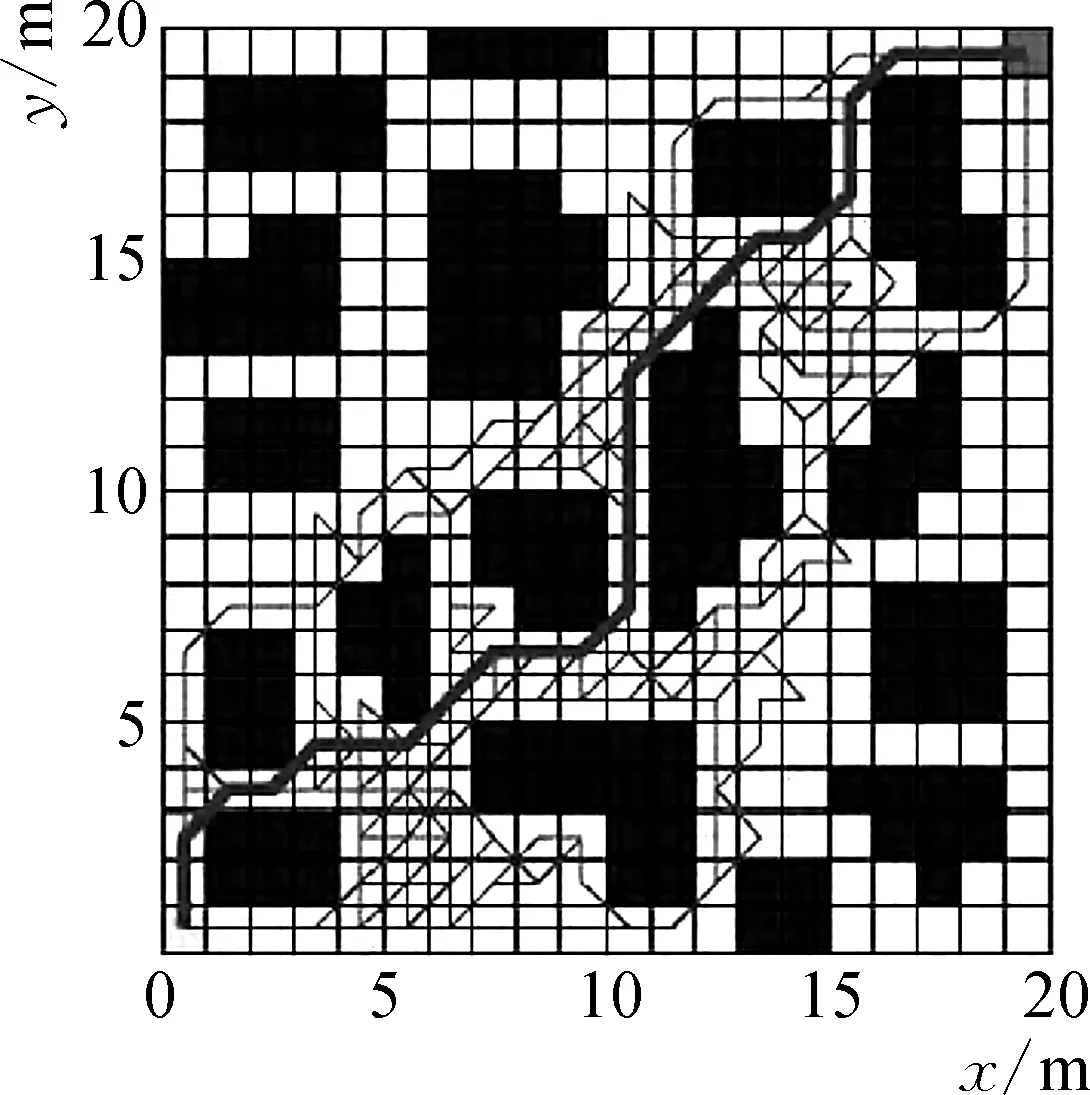
(a) 基本人工势场算法

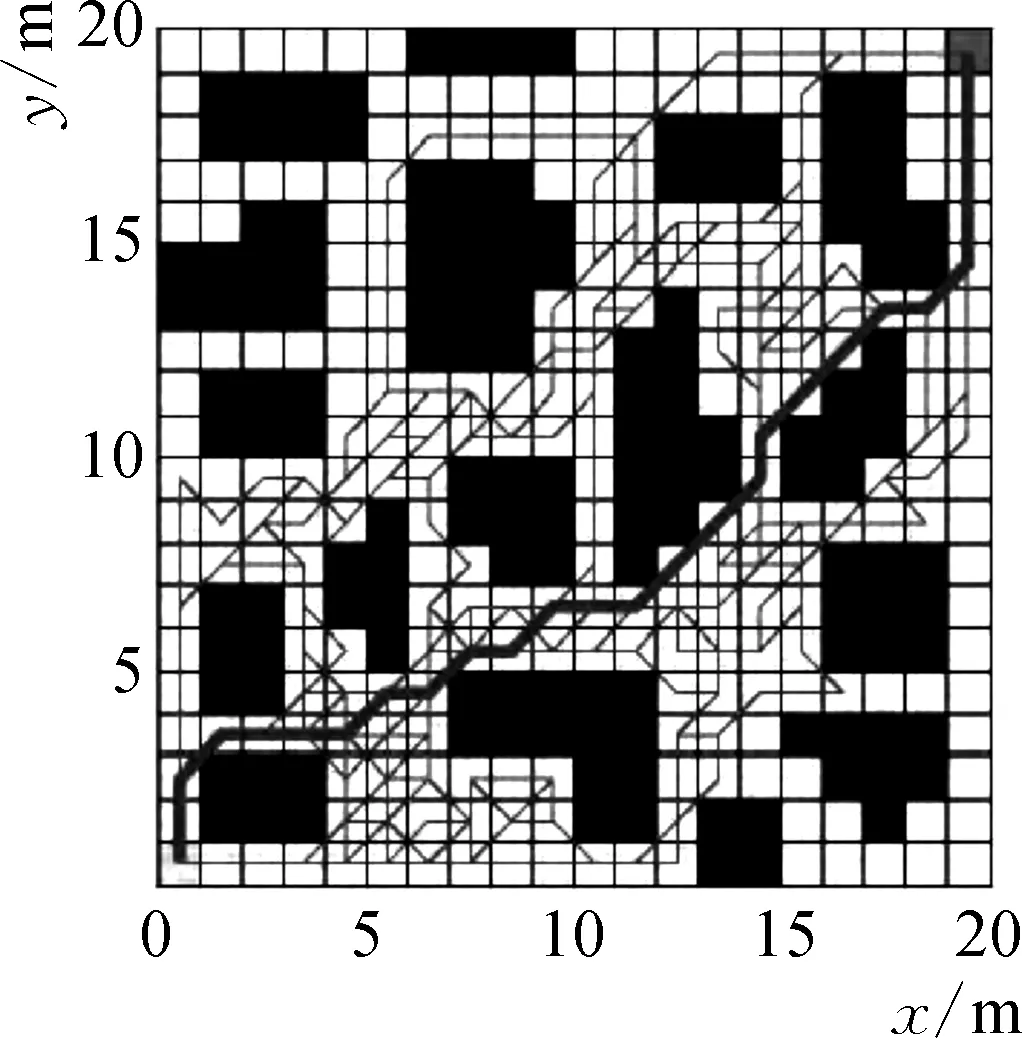
(b) 本文算法

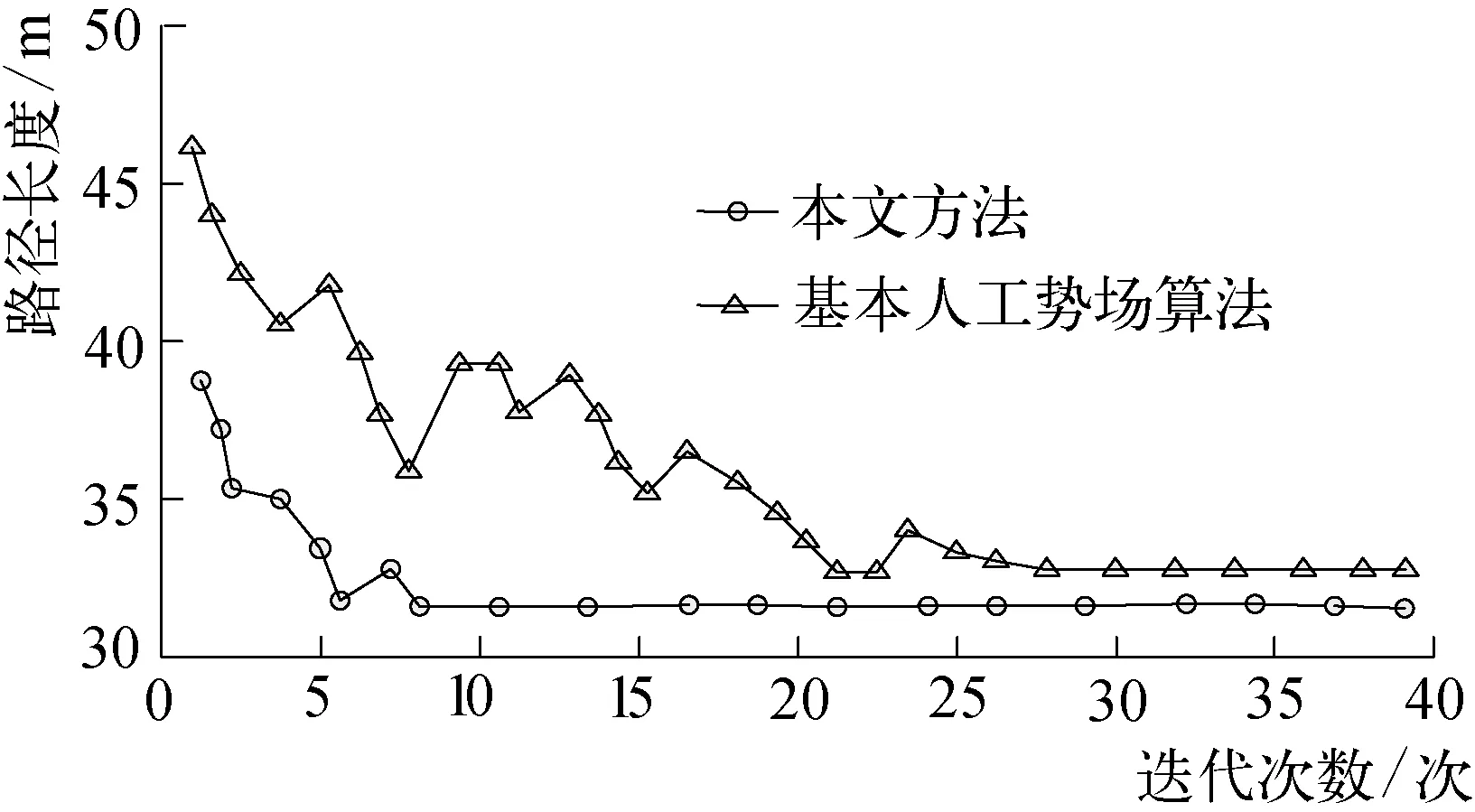
图3 复杂环境下路径长度迭代对比图Fig. 3 Comparison of path length iterations in hybrid environment

表1 两种算法测试结果对比Tab. 1 Comparison of test results of two algorithms

为使路径搜索能力更清楚地量化，采用所寻路径对环境的覆盖率这个参数量化，其表达式为

(16)

式中:Mp——算法检索到的方格数量；

Mf——自由方格的数量。

通过式(15)可以把两种算法的所寻路径对环境的覆盖率计算出来，基本人工势场算法的计算结果为56.89%，本文算法的计算结果是73.59%，本文算法所寻路径对环境的覆盖率提高了16.7个百分比。所寻路径对环境的覆盖率越大说明路径规划时搜索的范围越广，通过对比计算结果可知，本文算法得到最优路径的可能性最大，也就是说规划最优路径的能力更突出。

4 结论

1) 复杂环境下果园机器人使用的传统的基本人工势场算法进行路径规划存在死锁问题，本文算法使用障碍物检测算法识别路径计算出一个科学的路径中间点，同时优化了斥力作用，避免了局部最优解，可以得到更优的路径规划，所寻路径对环境的覆盖率提高了16.7个百分点，覆盖率越高，机器人全局寻优能力越强。

2) 本文算法充分使用收敛次数构建出反馈通道，这样就可以大大减少了迭代过程中的波动性，和基本人工势场算法相比，收敛过程更加平稳，大大减少了迭代次数，迭代次数减少了19次。

3) 本文算法不需要计算无效障碍物和斥力，大大降低了算法的运行时间，运行时间减少了近9 s，果园机器人的工作效率大大提高。