基于液压泵复数信号的log-SAM故障诊断方法研究

郑 直，李世峰，郭 洋，王志军，陈 志

(1.华北理工大学 机械工程学院，河北 唐山 063210；2.惠达卫浴股份有限公司，河北 唐山 063000；3.唐山师范学院 物理系，河北 唐山 063210；4.华北理工大学 轻工学院，河北 唐山 063000)

机械设备中的液压泵、滚动轴承和齿轮等起着动力输出和传动等重要作用，并已广泛地应用于航空航天、冶金和化工等重要领域。因此，如果上述元件发生故障，重则导致重大人员伤亡和经济财产损失。

目前，国内外学者已基于单源信号成功地对上述故障元件进行了大量研究：Li等[1-2]分别利用复合谱、信息熵、解析模态分解、形态学等方法对液压泵进行了故障诊断；侯文擎等[3]、程军圣等[4]、陆思良等[5]和Chen等[6]分别利用深度学习、总体经验模态分解、二维互补随机共振和稀疏编码等方法对滚动轴承进行了故障诊断；胡茑庆等[7]、张东等[8]、Shen等[9]和熊鹏等[10]分别利用经验模态分解、深度学习、迭代广义短时傅里叶变换和多分类直推式支持向量机等方法对齿轮进行了故障诊断；李志农等[11]和唐贵基等[12]分别利用变分模态分解和参数优化时变滤波经验模态分解等方法对转子进行了故障诊断。

当上述旋转机械设备发生故障时，会在不同方向表现出不同的振动形式，不同方向振动传感器所采集信号包含了不同数量和形式的故障特征信息。因此，将多源信号进行融合，可有效地提高故障诊断效率和精度。

目前，大量国内外学者基于全矢方法进行故障诊断。其思想是通过安装在同一截面两个相互正交的传感器来采集信号，融合各个信号中的特征信息，可全面地表达设备运行状态。刘嘉辉等[13]、马艳丽等[14]和林辉翼等[15]分别利用全矢谱和盲源分离、多为经验模态分解，稀疏分解等方法结合对滚动轴承进行了故障诊断；巩晓赟等[16]将全矢谱和小波包结合，实现了对齿轮的故障诊断；黄传金等[17]和孟雅俊等[18]分别利用全矢谱和二元经验模态分解相结合，对转子进行了有效的故障诊断。上述研究的分析过程为：将正交信号进行融合，之后在进行滤波处理，最后进行包络分析，实现故障诊断。

经过研究发现，当液压泵滑靴发生磨损故障时，耦合的机械振动和流体冲击振动形式会导致泵体振动加剧、振动形式复杂，所采集信号受到大量噪声污染、无法有效地表征故障特征信息。因此，在一定工况下，只利用单源信号很有可能导致所包含特征信息匮乏，无法实现对液压泵的故障诊断。但是，要抑制噪声影响，需要加入滤波方法进行滤波处理，再进行包络分析，导致诊断效率过低。

针对上述问题，本文在全矢思想基础上，引入log-SAM方法，提出复数信号和log-SAM相结合的新方法。

泵盖的不同方向振动信号蕴含不同数量和形式差异的故障特征信息。因此，将泵盖X轴和Y轴互相正交的两个方向信号进行融合，形成复数信号。

2019年7月，Moshrefzadeh等[19]提出log-SAM方法。首先，该方法将信号傅里叶变换后的幅值信息进行幂运算，并基于幅值运算结果和原相位信息进行傅里叶逆变换，得到改进信号；其次，对上述改进信号的傅里叶变换后的幅值信息求取平方包络，并进行对数运算；最后，对上述结果进行包络分析，实现故障诊断。本方法具有两方面优势：由于该方法引入了幂运算，如果参数选取适当，可有效地滤除噪声影响；具备包络分析能力。目前，由于log-SAM的新颖性，尚无其他学者对此进行相关研究。

本文所提方法利用log-SAM将复数信号进行包络分析，可有效地突显滑靴磨损故障特征信息，消除噪声影响，且无需引入消噪方法，最后基于总体和最优诊断结果，对该故障进行诊断分析。通过分析实测滑靴磨损故障信号，结果表明所提方法具有有效性和优越性。

1 复数信号

不同故障类型会引起不同的振动形式和振动传递路径，引起各个方向和部位的振动强度异同。因此，单独使用某一方向振动信号，很有可能导致所含特征信息匮乏、故障漏判或误判。

将互相正交的两个方向信号进行融合，可有效提高特征信息含量，对提高诊断精度有着十分重要的意义。因此，本文引入复数信号，其定义如下：

设在相互正交的X，Y方向上，分别存在x(t)和y(t)两个一维信号，将其构成复数信号为

z(t)=x(t)+jy(t)

(1)

式中，j为虚部。

2 log-SAM方法原理

对一维信号x(t)进行傅里叶变换

X(f)=FT{x(t)}=A(f)ejφ(f)

(2)

式中：A(f)为谱值信息；φ(f)为相位信息；j为虚部。

基于式(2)，进行傅里叶逆变换，得到

xm(t)=IFT{A(f)MOejφ(f)}

(3)

式中，xm(t)为改进信号，它由能够表征故障特征信息的谱值和原信号的相位重构而成。

其中，变量MO被称为数量级，a≤MO≤b(a，b为任意常数)。如果MO选取适当，xm(t)会突显特征信息，抑制噪声影响。

对xm(t)进行傅里叶变换，变换后的解析信号A{xm(t)}和平方包络谱SES{xm(t)}分别为

A{xm(t)}=xm(t)+jH{xm(t)}

(4)

(5)

此外，针对受到严重噪声污染的故障信号分析，Borghesani等[20]提出了对数-包络谱(log-envelope spectrum,LES)方法，它较式(5)中的SES更具有自适应性，其表达如式(6)所示

LES{x(t)}=|FT{logxm(t)2+ε}|

(6)

(7)

式(5)和式(7)反映了信号在频域中的调幅特征，所以SES和LSES被统称为频谱振幅调制(spectral amplitude modulation,SAM)方法。其中，式(7)中进行了对数运算，因此LSES又被称为log-SAM方法。需要注意的是，当式(3)中的MO=0时，log-SAM变为倒频谱预白化方法。

为了更好地展现诊断分析结果，将频率、MO和归一化谱值分别作为X轴、Y轴和Z轴，进行三维可视化。此外，还进行如下二维可视化：①在a≤MO≤b范围内，沿MO(Y轴)进行二维主视图分析，即将所有频率谱值投影在Y轴上，投影谱值就是在各个频率处的最大谱值，被称为最大谱，它能从总体反映故障诊断结果；②沿归一化谱值(Z轴)进行二维俯视图分析，建立谱值和颜色的关系，即在频率线(X轴)上颜色越深，说明该频率处的谱值越大，本文提出在此俯视图上筛选故障特征频率处的最大值，进行基于单一MO值的最优诊断结果分析。

因此，log-SAM方法可基于最大谱和最优诊断结果进行总体和最优故障诊断分析。它具有简单和高效特性，且无需信号的先验知识；同时，无需设置参数或筛选频带进行解调分析。事实上，它是一个具有非线性自适应滤波功能的包络分析工具。

3 基于液压泵复数信号的log-SAM故障诊断方法流程图

首先，采集两个互相正交的X轴、Y轴滑靴磨损故障单源振动信号；其次，将两单源信号融合为一个复数信号；再次，基于复合信号，利用log-SAM方法进行分析；最后，筛选最优故障诊断结果，基于总体和最优诊断效果，实现故障诊断。

所提方法流程如图1所示。

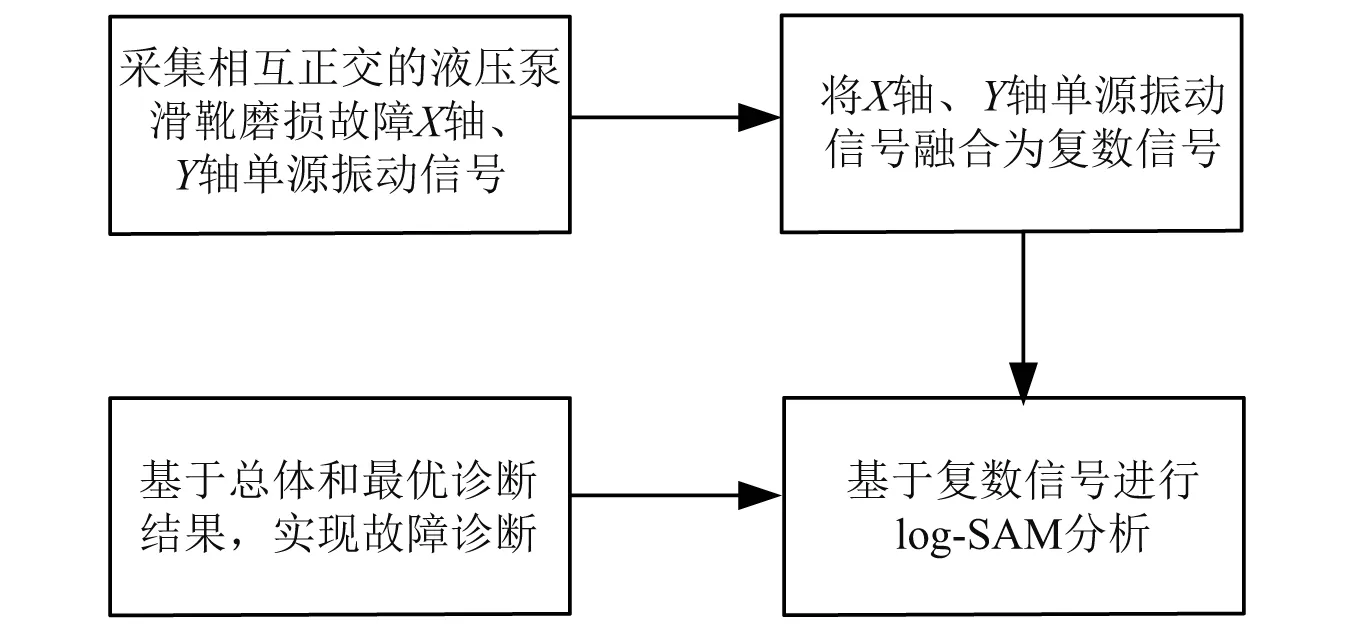
图1 方法流程图Fig.1 The flow chart of the proposed method

4 液压泵故障信号分析

4.1 实验方法

为了验证所提方法的有效性和优越性，以柱塞数为7的MCY14-1B型斜盘式轴向柱塞泵为实验对象，以50 kHz的采样频率对泵盖的X轴、Y轴和Z轴振动信号进行采集，其中X轴和Y轴信号相互正交。额定转速为1 470 r/min，泵出口压力调定为10 MPa，滑靴磨损故障特征频率为171.5 Hz[21]。实验系统如图2所示。

图2 斜盘式轴向柱塞泵的实验系统Fig.2 The swashplate axial plunger pump experiment system

4.2 滑靴磨损故障信号

基于X轴、Y轴和Z轴采集的滑靴磨损故障信号如图3～图5所示。

图3 X轴原信号Fig.3 The original signal of X-channel

图5 Z轴原信号Fig.5 The original signal of Z-channel

经分析图3～图5可知，在滑靴磨损故障特征频率171.5 Hz及其倍频处，无法有效地呈现故障特征信息、且在其它频率处受到很大噪声干扰影响。

4.3 基于X-Y双源信号的全矢谱分析

为了说明所提方法的有效性和优越性，本文利用基于全矢谱方法对互相正交的X轴、Y轴振动信号进行分析，图6为分析结果。

经分析和对比图6、图3(b)的X轴原信号频谱、图4(b)的Y轴原信号频谱、图5(b)的Z轴原信号频谱可知，全矢谱方法可以将在滑靴磨损故障特征频率171.5 Hz及其倍频处的故障特征信息有效地提取出，但是在其它频率处也受到较大噪声干扰影响。因此，全矢谱方法可以较好地实现滑靴磨损故障的有效诊断。

图4 Y轴原信号Fig.4 The original signal of Y-channel

图6 基于全矢谱方法所得结果Fig.6 The result got based on full vector spectrum

4.4 基于log-SAM的单源信号分析

为了说明所提方法的有效性和优越性，本文利用基于log-SAM方法分别对X轴、Y轴和Z轴单源振动信号进行分析，其中-0.5≤MO≤1.5。

4.4.1 基于log-SAM的X轴单源故障信号分析

基于X轴单源故障信号的分析结果如图7所示。

图7 基于log-SAM的X轴单源振动信号所得结果Fig.7 The result got based on log-SAM for X-channel signal

图7(a)中的X轴、Y轴和Z轴分别代表频率、MO和归一化谱值，其中MO分别以0.1的步长计算三维频谱分布。

图7(b)为图7(a)沿谱值(Z轴)的二维俯视图，其中频率线上颜色越深，代表该频率谱值越大。由图7(a)和图7(b)可知，在滑靴磨损故障特征频率171.5 Hz及其倍频处都存在明显的故障特征信息；在50 Hz的-0.5≤MO≤-0.2内、100 Hz的-0.5≤MO≤0.1内、225 Hz的-0.5≤MO≤-0.3内都存在较大噪声干扰。

图7(c)为图7(a)沿MO(Y轴)的二维主视图。在-0.5≤MO≤1.5内，它是所有频率谱值在Y轴上的投影，投影谱值即为各个频率处的最大谱值，被称为最大谱，它能从总体反映故障诊断结果。通过分析图7(c)和图3(b)的X轴原信号频谱可知，只有在滑靴磨损故障特征频率171.5 Hz及其1倍频和2倍频处的故障特征信息被有效提地提取出，但在其它频率处受到严重噪声影响。

因此，从最大谱角度可知，log-SAM具有一定的故障诊断能力，但诊断效果一般。

经分析图7(b)可知，当MO=1.1时，在滑靴磨损故障特征频率171.5 Hz及其倍频处的颜色最深，即其对应谱值为最大，为最优故障诊断结果，且比MO=0时的倒频谱预白化方法效果好。选取MO=1.1所对应的改进信号进行分析，如图8所示。

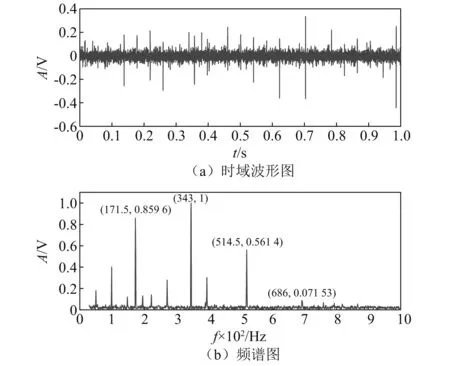
图8 MO=1.1的最优诊断结果(基于X轴单源故障信号)Fig.8 The best result of fault diagnosis in case of MO=1.1 (based on X-channel signal)

由图8所示的最优诊断结果，将其和图3(b)的X轴原信号频谱对比可知，滑靴磨损故障特征频率171.5 Hz及其绝大部分倍频处的故障特征信息都被有效地提取出，在其它频率处的噪声也被得到一定抑制。

同样，将图8(b)的最优诊断效果和图6基于全矢谱方法所得结果进行对比和分析可知，前者可有效地提取出在滑靴磨损故障特征频率171.5 Hz及其部分倍频处的故障特征信息，但在其它频率处也受到稍大噪声影响。

因此，从最优诊断结果角度可知，log-SAM能够基于X轴单源故障信号，实现对滑靴磨损故障的有效诊断，但效果较全矢谱方法差。

4.4.2 基于log-SAM的Y轴单源故障信号分析

基于Y轴单源故障信号的分析结果如图9所示。

图9 基于log-SAM的Y轴单源振动信号所得结果Fig.9 The result got based on log-SAM for Y-channel signal

基于图9的分析可知，在滑靴磨损故障特征频率171.5 Hz及其倍频处，没有出现故障特征信息，且在其它频率处存在较严重噪声干扰；100 Hz的-0.5≤MO≤1.5内、400 Hz的-0.5≤MO≤-0.1内存在严重噪声干扰。

因此，log-SAM无法基于Y轴单源故障信号进行有效的故障诊断。

4.4.3 基于log-SAM的Z轴单源故障信号分析

通过分析MCY14-1B型斜盘式轴向柱塞泵的结构可知，当滑靴发生磨损故障时，滑靴对于斜盘水平机械冲击将加剧，Z轴单源振动信号较其它处信号烈度大，往往含有较多故障特征信息。因此，本文为了突出所提方法的有效性和优越性，将基于Z轴单源振动信号进行分析，结果如图10所示。

图10 基于log-SAM的Z轴单源振动信号所得结果Fig.10 The result got based on log-SAM for Z-channel signal

同样，由图10可知，log-SAM无法提取出在滑靴磨损故障特征频率171.5 Hz及其倍频处的故障特征信息，且在其它频率处受到严重的噪声干扰；100 Hz的-0.5≤MO≤1.5内存在严重噪声干扰。

因此，针对含有丰富故障特征信息的Z轴信号，log-SAM也无法成功地实现故障诊断。

4.5 基于log-SAM的X-Y双源融合的复数故障信号分析

为了增加故障特征信息量，本文利用基于log-SAM方法对X-Y双源融合的复数故障信号进行分析，其中-0.5≤MO≤1.5。结果如图11所示。

图11 基于log-SAM的X-Y轴复数振动信号所得结果Fig.11 The result got based on log-SAM for X-Y complex signal

对图11(a)和图11(b)进行分析可知，在滑靴磨损故障特征频率171.5 Hz及其倍频处，出现了非常明显的故障特征信息，噪声干扰较小；只有100 Hz的1.3≤MO≤1.5内，存在较大噪声干扰。

图11(c)中，在滑靴磨损故障特征频率171.5 Hz及其倍频处，存在很大幅值，只有在很少频率处出现噪声干扰。从总体角度分析，故障特征提取效果要好于基于log-SAM的X轴单源振动信号所得结果如图7(c)所示。

因此，从最大谱角度可知，基于log-SAM对复数振动信号具有较强的故障诊断能力，效果要好于对X轴单源振动信号的。

由图11(b)可知，当MO=1.1时，在滑靴磨损故障特征频率171.5 Hz及其倍频处的颜色最深，即其对应谱值为最大，为最优故障诊断结果，且比MO=0时的倒频谱预白化方法效果好。选取MO=1.1所对应的改进信号进行分析，如图12所示。

图12 MO=1.1的最优诊断结果(基于X-Y轴复数振动信号)Fig.12 The best result of fault diagnosis in case of MO=1.1(based on X-Y complex vibration signal)

对比图12的最优诊断效果、图3(b)的X轴原信号频谱、图4(b)的Y轴原信号频谱可知，图12中的滑靴磨损故障特征频率171.5 Hz及其倍频处的故障特征信息全部得到了有效突显，且噪声抑制效果最好。

通过分析和对比图12(b)的最优诊断效果和图6基于全矢谱方法所得结果可知：二者在故障特征频率171.5 Hz处的幅值基本一样；前者在2，3，4和5倍频处幅值较后者的高出很多；除上述频率外，后者在其它很多频率处也存在幅值，且较前者高。因此，所提方法可有效地提取故障特征信息、抑制噪声影响，其最优诊断效果要优于基于X-Y双源信号的全矢谱方法。

图12(b)的最优诊断效果出现在MO>1内，从式(7)角度说明log-SAM在此范围内具有突显A{xm(t)}中的故障特征信息、抑制噪声能力。

因此，从最优诊断结果角度可知，log-SAM能够基于复数信号有效地对滑靴磨损故障进行诊断。

5 结 论

液压泵同时受到复杂的机械和流体振动影响，滑靴磨损故障振动信号极易受到噪声污染，且单源信号往往含有较低的故障特征信息量。因此，本文提出了一种基于复数信号的log-SAM新方法。通过分析实测滑靴磨损故障振动信号可知，所提方法具有很强特征提取能力，可有效抑制噪声影响，并得出如下结论：

(1) 在液压泵端盖同一截面、两个互相正交信号融合的复数信号较单源信号含有更丰富的故障特征信息。

(2) 提出了最优故障诊断分析方法，且复数信号log-SAM的最优诊断效果要优于基于单源信号log-SAM方法、全矢谱方法和倒频谱预白化方法。

(3) 基于复数信号log-SAM的总体诊断效果要优于基于单源信号log-SAM的总体诊断效果。