阻振质量-刚度-阻尼材料配置同步优化的基座声学设计
2021-03-31王语嫣杨德庆
王语嫣,杨德庆
(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240;2.上海交通大学 海洋工程国家重点实验室,上海 200240;3.上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240)
船舶辐射噪声研究主要针对机械噪声、推进器噪声以及水动力噪声展开,取得了显著进展,也面临新的挑战[1]。Inoue等[2]对齿轮箱体上阻振质量拓扑分布进行优化设计,优化结果与未安装阻振质量相比减小了3 dB。刘见华等[3]在板上平行排列多个阻振质量,采用波动分析法进行数值计算,与模型试验结果比对之后发现,多个阻振质量在阻抑结构声传递方面具有良好的效果。高森[4]分析了基座结构的厚度以及肋间距对辐射噪声的影响,指出随着基座结构的厚度减小以及肋间距减少,其辐射噪声都有所降低。夏齐强等[5]通过在双层壳体间布置非均匀的肋骨以及阻振质量、黏弹性夹层,明显降低了壳体振动响应,使得辐射噪声有效减小。杨德庆等[6]以自由阻尼层结构为研究对象,将结构拓扑优化方法引入到阻尼材料配置优化中,建立了阻尼材料配置优化拓扑基结构。上述研究表明,阻振质量、阻尼材料和构件尺寸(构件刚度)对减振降噪有重要作用。
船上主要动力设备大多安装在船体基座上,并通过基座与船体结构连接,因此设备的机械振动也通过基座传递到船体并向外辐射噪声。因此,进行基座的声学优化有利于降低船体辐射噪声。本文基于文献[7]的研究成果,探究阻振质量-基座刚度-阻尼材料等综合设计对辐射噪声的影响,提出以声功率为约束条件,在减小一定噪声级的基础上实现质量最小化的声学优化设计方法。
1 考虑辐射声功率的基座声学设计
基座作为机械动力设备与船体结构的连接部分,是振动能量传递的重要途径。王国治等[8-9]对基座参数对舰船结构振动及声辐射的影响进行了研究与探讨,发现适当减弱基座结构更有利于降低船体外板振动。熊琳[10]从理论与实践两方面着手,阐述了基座阻抗对隔振效果的影响。基座阻抗值越大,则传递到船体的振动越小,基座隔振效果越好。杨康等通过阻抗综合优化设计,获得了高传递损失基座。
以往对船舶基座的研究大多侧重于减弱船体外板振动从而降低船体辐射噪声,直接考虑辐射噪声指标的基座优化设计的研究较少见。对于舰船声隐身而言,降低船体辐射噪声是最终设计重点。对于复杂结构来讲,辐射噪声并不与振动成比例。本文理论创新点主要在于提出基于动态代理模型的基座声学优化设计模型及优化方法,采用径向基函数神经网络(即:RBF神经网络)对样本点构建动态代理模型,使得直接对基座的声学优化设计成为可能,实现对舰船声隐身性能的控制。本文基于该出发点,以舰艇舱段为背景,研究从阻振质量、基座刚度和阻尼材料配置等三方面入手,以声功率为约束条件进行的基座声学优化设计。
声传播伴随着能量的传播,用单位时间内通过垂直于声波传播方向的单位面积的能量表示。在声学特性参数中,声功率表示声源辐射的总强度,与测量距离以及测点的具体位置无关,具备更好的可对比性。
声功率定义如下

(1)

声功率级定义如下
(2)
式中:LW为声功率级,dB;w0=10-12W为基准声功率;w为声功率。
对多个不相干声源,根据叠加原理计算合成声功率级,其公式如下
L=10lg(∑10LWi/10)
(3)
式中,LWi为各频率下对应的声功率级。
声振动的能量范围极其广阔,使用对数标度比绝对标度更加方便;且接收声振动之后的主观“响度感觉”更近于正比于强度的对数[11]。因此,本文采用声功率级来表征辐射噪声的强弱。
(4)
2 基座声学优化设计的阻振质量-基座刚度-阻尼材料综合配置法
2.1 采用阻振质量措施的基座声学优化模型
以基座结构质量最小化为目标,对阻振质量进行优化设计的声学优化模型的数学列式如下
(5)
式中:mass为基座中可优化部分总质量;M=[d1,…,dm]T为阻振质量设计变量向量;LWI为基座近似代理模型的声功率级计算结果;LWV为基于基座有限元模型的辐射噪声声功率级计算结果;dmin,dmax分别为阻振质量-方钢的厚度设计下限值和上限值;LW0为原始设计基座的辐射声功率级;LW1为基座声学优化设计后辐射声功率级目标值;R为降噪值;ε为较小正数。
2.2 阻振质量-基座刚度综合设计的基座声学优化模型
以基座结构质量最小化为目标,阻振质量-基座刚度同步优化设计的声学优化模型的数学列式如下
(6)
式中:tmin,tmax分别为构成基座的面板、腹板和肘板等各类板厚度设计下限值和上限值;其它变量含义同式(5)。
2.3 阻振质量-基座刚度-阻尼材料综合配置的基座声学优化模型
以基座结构质量最小化为目标,阻振质量-基座刚度-阻尼材料综合配置优化设计的声学优化模型的数学列式如下
(7)
式中:ck∈{0,1}为在位置k处是否贴敷阻尼材料,0为不贴敷,1为贴敷;其它变量含义同式(6)。
2.4 阻振质量-基座刚度-阻尼材料综合优化设计模型与声学分析模型间的映射变换
根据杨康等的研究,大质量方钢采用板单元模拟其振动计算结果与实验测定值接近。因此,作为阻振质量的方钢的设计变量包括拓扑分布及尺寸优化两个方面。在指定位置上,若代表方钢的板单元厚度为0,则代表此处不设置大质量方钢,若板单元厚度不为0,则表示在此处设置该尺寸厚度的大质量方钢。对于基座刚度设计,基座刚度影响因素众多,在基座类型已知(分离式基座)、外廓尺寸及制造材料已定(钢材)的基础上,由基座面板、腹板和肘板的厚度决定,因此以这些板的厚度为设计变量,通过厚度尺寸变化来改变基座刚度大小,该变量为连续设计变量。阻尼材料拓扑优化设计含有两个设计参数,其一为阻尼材料厚度设计参数,其随贴敷位置处板材厚度尺寸的变化而变化,为连续设计变量。阻尼材料拓扑设计变量属于离散变量。在指定位置不贴敷阻尼,则阻尼材料拓扑值为0;或贴敷阻尼,阻尼材料拓扑值为1。因此,在含有阻尼材料拓扑优化的列式(7)中,无法采用常规的梯度下降法进行求解,需要进行一定改造。
为应对这种情况,本文采用文献[12]给出的方法对优化列式(7)中的阻尼材料设计变量进行连续化映射变换,使阻尼材料拓扑设计值由离散的0或1值映射到区间[0,1]上连续取值,根据这个结果构建代理模型,在得到代理模型的优化结果后进行逆映射变换,将连续化后的阻尼材料拓扑设计值还原为离散值(0或1)。
本文选用反正切映射函数,表达式为
(8)
其函数曲线如图1所示。

图1 反正切映射函数曲线Fig.1 Inverse tangent mapping function
在区间[0,0.5),映射函数f(h)逼近于0;在区间(0.5,1],映射函数f(h)逼近于1。
2.5 代理优化模型及求解
优化问题式(5)、式(6)和经过模型间映射变换的优化问题式(7)可采用代理模型方法[13]求解。从技术上看,代理模型的构建包括静态代理模型技术和动态代理模型技术。静态代理模型技术一次性从设计域中获得训练所需要的样本点,而动态代理模型技术是先从设计域中获得训练所需要的样本点,然后通过初步代理模型的预测值不断添加新的样本点至训练集中,直到满足精度要求为止。对于船舶这类超大型结构,其振动噪声分析的计算量巨大,计算周期长。采用代理模型方法计算,可以避免振动声学计算的巨大耗时,更易面向工程应用。具体方法是:首先在软件Isight平台上选取样本点,通过声学计算分析模型建立声学分析动态代理模型;之后,基于该声学分析动态代理模型,进一步求解优化模型式(5)、式(6)和式(7)。
声学优化设计的具体计算流程如图2所示。

图2 声学优化设计流程Fig.2 Acoustic optimization design process
本文采用最优拉丁超立方设计方法选取样本点。最优拉丁超立方设计方法样本点分布均匀,相较于随机拉丁超立方设计方法,其因子和响应的拟合来得更加精确。同样通过最优拉丁超立方设计方法随机选取若干检验点作为该声学分析代理模型的误差分析测试集,以便进一步检验该声学分析代理模型的精度,使结果更为真实可信。
采用RBF神经网络方法建立动态代理模型。基于RBF神经网络的计算方法,拟合误差较小,更适用于工程估算[14-17]。
其原理如下:
以待测点与样本点之间的欧几里得距离为自变量,即假设x1,…,xN∈Ω⊂RN代表一组输入向量,gi≡g(‖x-xf‖c)∈R(j=1,…,N)是基函数。其中‖x-xj‖是欧几里得距离:(x-xj)T(x-xj),且0.2≤c≤3。
Isight优化平台中包含上述代理模型技术。因此,直接利用Isight软件优化设计本文研究内容。
2.6 基座优化模型与方法的实验验证
鉴于缺乏声学测量实验室条件,对于本文提出的基座声学优化设计方法,我们间接通过对一含基座板架的振动优化设计实验验证。通过进行阻振质量-基座刚度综合优化设计来减小板架振动。
实验基座板架模型结构图见图3,实验基座板架现场图见图4。

图4 实验基座板架Fig.4 Base pallet in experiment

图3 基座板架模型Fig.3 Model of base pallet
其优化设计的数学列式如下
(9)
式中:d1,d2,d3分别为布置于基座周围的方钢、腹板底部的方钢、腹板中部的方钢所处位置的厚度尺寸;t1,t2,t3分别为基座面板、腹板、肘板的厚度尺寸;LAI为根据近似代理模型计算得到的外板平均振动总级;LAV为通过动力学模型计算得到的外板平均振动总级;LA0为含原始设计基座板架的外板平均振动总级;LA1为外板平均振动总级优化目标值;ε为一极小正数。
根据实验进行模态修正后得到的优化结果及板架在10~2 000 Hz频段内的计算与实验结果见表1。
从表1中可看出,在10~2 000 Hz频段内,原始基座板架与优化基座板架的实验测量结果与有限元计算结果之间相差均不超过2 dB,误差在可接受范围之内,说明该基座优化设计模型是有效的。结构振动与结构辐射噪声之间是相互作用的,该实验结果可以间接验证本文模型和方法应用于基座声学优化设计中的可行性。

表1 基座板架优化设计结果Tab.1 Results of base pallet optimal design
3 基座声学优化设计算例
以某船用基座指定频段内降噪优化设计为例。优化设计变量包括多个作为阻振质量的方钢的截面尺寸及拓扑布置,基座面板、腹板和肘板的厚度,阻尼材料的拓扑分布及其厚度,通过阻振质量、基座刚度及阻尼材料配置同步优化,获得低辐射噪声基座设计。
3.1 基座声学优化模型
图5所示为某水面舰的含基座舱段有限元模型。图6中基座尺寸参数为:基座面板2 000 mm×150 mm×12 mm(长度×宽度×厚度),基座腹板2 000 mm×250 mm×8 mm(长度×宽度×厚度),基座肘板150 mm×300 mm×8 mm(上边长×下边长×厚度);基座制造所用钢材:密度为7 850 kg/m3,弹性模量为206 GPa,泊松比为0.3。图7所示为阻振方钢布置图,分别在基座腹板中部、基座腹板与板架连接处、基座周围敷设阻振方钢。图8所示为阻尼材料布置图,分别在基座面板、腹板、肘板上贴敷1.5倍阻尼材料。
图8 阻尼材料的布置示意Fig.8 Damping material layout

图7 阻振质量-方钢的布置示意Fig.7 Vibration resistance mass-square steel layout

图6 某舱段内基座结构图(mm)Fig.6 Structural model of base structure in a cabin(mm)

图5 某舱段内基座有限元模型Fig.5 Finite element model of base structure in a cabin
通过1/3倍频程频响分析得到原始设计基座的振动响应。
本文基于Virtual.Lab软件,采用声学边界元方法计算该舱段在基座面板位置激励一单位力时产生的空气辐射噪声。其声学计算模型如图9所示,其中外包围球体为计算声功率级所用到的包络球面,包络球面的边界元模型为导入的该舱段边界元模型。

图9 声学计算模型Fig.9 Acoustic calculation model
只采用阻振质量的基座声学优化模型的数学列式如下
(10)
式中:mass为基座可优化部分总质量,其数学表达式为
mass=10.048d1+3.14d2+3.14d3
(11)
d1,d2,d3分别为布置于基座周围的方钢、腹板底部的方钢、腹板中部的方钢的厚度尺寸;LWI为根据近似代理模型计算得到的舱段辐射噪声声功率级;LWV为通过振动声学模型计算得到的舱段辐射噪声声功率级;LW0为含原始设计基座的舱段模型在10~2 000 Hz频率区间的辐射噪声声功率级;LW1为声功率级优化目标值;ε取为0.3 dB。
进行阻振质量-基座刚度同步优化设计的基座声学优化模型的数学列式如下
(12)
式中:mass为优化部分总质量,其数学表达式为
mass=10.048d1+3.14d2+3.14d3+
4.71t1+7.85t2+4.416t3
(13)
t1,t2,t3分别为基座面板、腹板、肘板的厚度尺寸;其它各参数同列式(10)。
阻振质量-基座刚度-阻尼材料综合配置优化设计的基座声学优化模型的数学列式如下
(14)
式中:mass为优化部分总质量,其数学表达式为
mass=10.048d1+3.14d2+3.14d3+
[1.65f(z1)+7.85]·0.6t1+
[1.65f(z2)+7.85]·t2+
[1.65f(z3)+7.85]·0.562 5t3
(15)
z1,z2,z3分别为基座的面板、腹板、肘板处阻尼材料拓扑分布设计变量;其它各参数同列式(12)。
3.2 优化结果及讨论
基于Isight软件平台,采用RBF神经网络方法求解优化问题式(10)、式(12)和式(14)。
通过1/3倍频程频响分析得到含原始设计基座舱段辐射噪声为77.67 dB。本算例辐射噪声优化目标为74.67 dB,较原始设计减少3 dB。在Isight优化平台中选用序列二次规划方法作为优化算法求解,得到三种近似代理模型优化结果,见表2~表4。

表2 阻振质量优化设计结果Tab.2 Results of vibration resistance mass optimal design

表3 阻振质量-基座刚度同步优化设计结果Tab.3 Results of vibration resistance mass-base stiffness optimal design
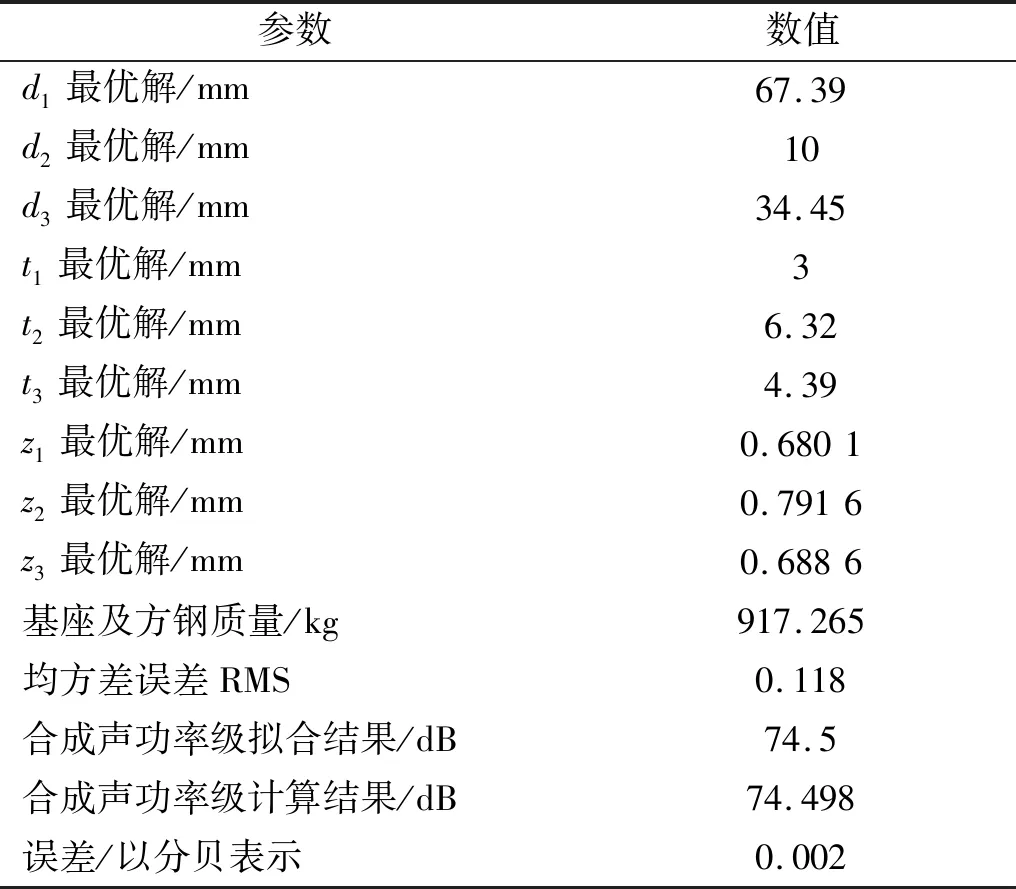
表4 阻振质量-基座刚度-阻尼材料综合优化设计结果Tab.4 Results of vibration resistance mass-base stiffness-damping material optimal design
原始模型计算结果以及三个优化设计模型的优化结果见表5。其中,阻尼参数为0或1表示在该位置处不贴敷或贴敷阻尼材料。
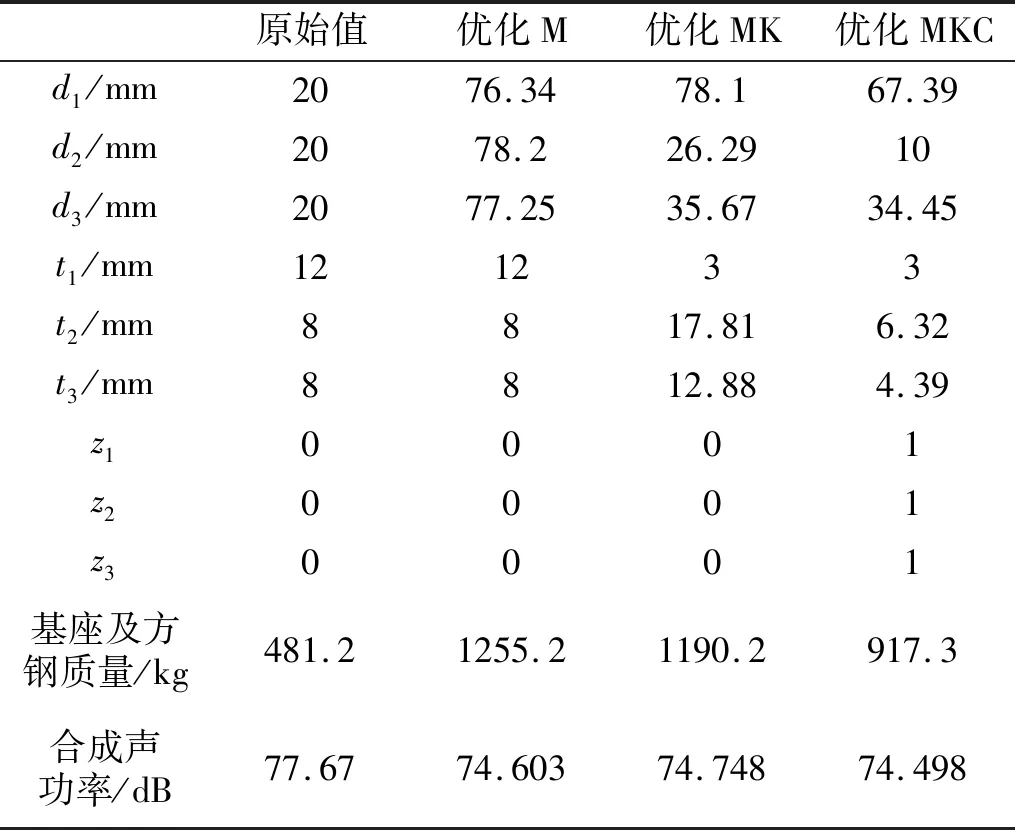
表5 四个模型声学计算结果对比Tab.5 Comparison of acoustic results for four models
从表中对比可以看出,在达到减小辐射噪声目标(即辐射声功率级降低3 dB)的基础上,阻振质量-基座刚度-阻尼材料综合配置优化结构总质量增加最小,说明了基于该模型的阻振质量-刚度-阻尼材料多参数优化设计方法是一种行之有效的优化方法。
将三个优化模型与原模型比较,在10~2 000 Hz频率区间内的1/3倍频程声功率计算结果如图10曲线所示。
从图10可以看出,原模型的高辐射噪声出现在200 Hz以后的频率区间,在中高频区间,三个优化模型的降噪结果较好。而在低频段区间,三个优化模型的降噪效果一般。

图10 四个设计模型的声学计算结果比较Fig.10 Comparison of acoustic results for four designed models
4 结 论
本文分别从阻振质量优化、阻振质量-基座刚度同步优化、阻振质量-基座刚度-阻尼材料配置综合优化三个方面入手,基于声功率级约束,采用RBF神经网络方法构建动态代理模型,进行了基座声学优化设计研究。初步研究表明:
(1)直接进行基座声学优化设计是可行的,通过基座减振优化进而达到基座声学优化效果的以往设计方法是可被替代的。
(2)基于阻振质量优化设计、阻振质量-基座刚度同步优化设计、阻振质量-基座刚度-阻尼材料综合优化设计三个优化模型均能达到预期降噪优化目标,本文算例中高频域降噪效果明显,在低频域降噪效果一般。
(3)阻振质量-基座刚度-阻尼材料配置综合优化设计模型尽管设计变量最多,优化过程复杂,但在三个优化模型中优化效果最好,更易达到优化目标,且质量增加不大。
