基于应变监测的预应力混凝土梁桥安全评估

张瑞斌

（山西省交通新技术发展有限公司，山西 太原 030012）

早期建设的桥梁，经历几十年的岁月，风化、车辆荷载、温度、甚至是其他微小的因素都可能使桥梁本身的结构性受到一些影响[1-2]。笔者针对一座预力混凝土I型梁桥进行分析，探讨桥梁老劣化后桥体的变形能力与预力损失程度，并利用桥梁监测与数值模拟掌握变形的安全范围，以确保路人行车及桥体安全。

1 数值模型概况

针对某预力混凝土I型梁桥，采用有限元法进行数值模拟分析，使用Midas Civil分析桥梁的变形、应力、断面预力等，并搭配监测数据来调校模型，使模型能更符合桥梁现状。

本文讨论的梁桥，桥全长360 m，全宽40 m，为单向四车道，宽19.6 m。头尾第一跨与第十跨的跨长为20 m，第二跨至第九跨的跨长均为40 m，其桥梁立面图如图1。

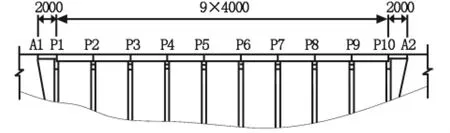
图1 桥梁立面图（单位：cm）

图1每跨的上部结构形式为简支预应力混凝土梁，主要为主梁与桥面板连结的合成断面组成。由于此桥于第七跨与第十跨发现有结构性裂缝及非结构性裂缝产生，因此将两跨所有梁换成新设计的梁。新桥跨与旧桥跨结构模型虽然近乎相同，但在材料性质与预应力筋性质上却大不相同，且在断面部分上，桥板厚度、梁腹板厚度、端隔梁厚度、中隔梁厚度等等也有些许差异。建立预应力混凝土梁桥数值模型时，由于大多数跨结构相同，仅差别于新旧桥跨及跨长，因此将旧桥跨（更换前）与新桥跨（更换后）区分出来做分析，建立40 m新桥跨、40 m旧桥跨、20 m新桥跨、20 m旧桥跨4种模型。

结构概念上，桥体为直线型预应力混凝土梁桥，为考虑实际上桥面板与隔梁在不同主梁间的传力效应，选择以梁格模型来做为有限元仿真的结构系统，40 m新桥与旧桥上部结构模型如图2所示，20 m新桥与旧桥上部结构如图3所示，其中桥面板以框线表示，主梁与隔梁则以实心表示。

图2 40 m新桥与旧桥上部结构模型

图3 20 m新桥与旧桥上部结构模型

2 基于监测数据的数值模型修正

以数据为依据所建立的数值模型，因并未设定工期与收缩徐变，数值模型不会受到收缩徐变的影响，预力损失的程度也非常轻微，模型情况较合乎刚完工时的状态。本文讨论的桥梁已运营数十年，预力损失对于结构性能有一定程度上的影响，因此数值模型的特性并不会与实际桥梁状况吻合[1]。为了让模型能够符合桥梁现况，利用车辆载重试验的结果搭配理论进行修正，使模型挠曲刚度与现状接近，对于建立监测管理阈值有很大的帮助。

2.1 现场试验与监测数据

基于健康监测系统平台，将数值模型搭配现场试验做交互比对。本文涉及的传感器类别主要为应变计及温度计。为测量桥梁受车辆载重试验的应变反应，于各梁跨径中间点的梁底处与腹板中部H处安装静态应变计与温度计，如图4所示。如图5为车辆载重试验的主梁编号，以单轴应变计为量测仪器，主要用来监测主梁的挠曲应力变化，由于应变计测到的应力变化相当容易受到混凝土曝晒于日照下引起温度变化的影响，因此选择于应变计旁安装温度计，以记录温度变化，用来校正应变计受温度效应的影响与消除温度飘移现象[3-4]。

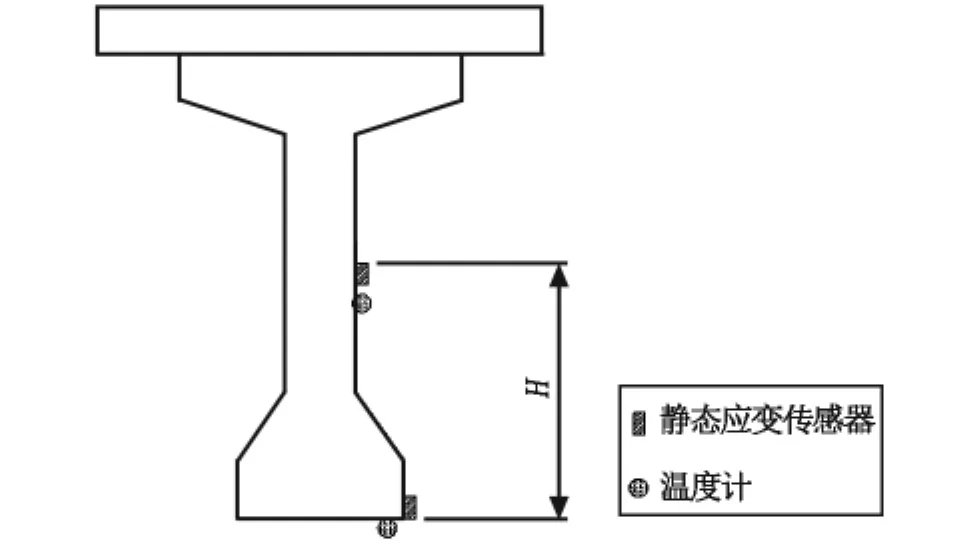
图4 静态应变计与温度计位置

图5 G5梁位置示意图

2.2 载重试验

对各跨分别进行车辆载重试验，将一选定车辆开至每跨G5号梁跨中后进行数据监测分析，如图5所示。桥梁第七跨与第十跨因老劣化较为严重，目前已更换为新设计后的主梁，在做数据整理时，选定将第七跨为40 m桥的试验对照组，第十跨则做为20 m桥的试验对照组，从而比较新旧桥的老劣化差异。

最后将跨径40 m各跨的车载试验结果汇整如表1，跨径20 m各跨结果汇整如表2（表中正号代表拉应变，负号则代表压应变）。桥梁上部结构为简支承形式，虽然受到温度变化的影响较微小，但数据仍将温度造成的影响排除掉，车载试验的结果纯粹为车辆载重引起的应变增量。

表1 40 m各跨车载结果汇整

表2 20 m各跨车载结果汇整

2.3 模型修正

相近跨距、材料性质、断面形状的桥跨才能有效地进行模型修正，40 m桥跨与20 m桥跨在跨距、材料性质、断面形状上皆有很大的差异，因此选择将跨径40 m桥与跨径20 m桥分开个别比较。利用荷载试验结果计算出各跨的曲率半径（两点高度差/两点应变差），再通过计算出的车辆荷载作用下的弯矩值，将弯矩与曲率半径相乘可得到各跨主梁的挠曲刚度EI，将此EI值称为等效EI值，再将等效EI值除以通过模型计算出的断面惯性矩I值，最后即可得出等效弹模E*，并将E*代入数值模型中，就能模拟出接近于各跨现状的等效挠曲刚度，计算结果如表3、表4所示。

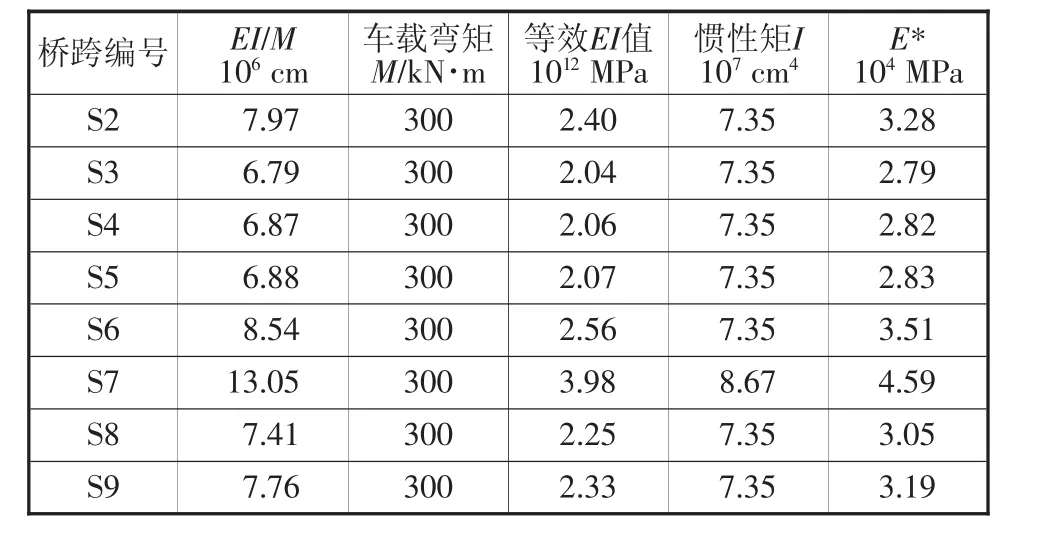
表3 40 m各跨等效EI与E*表

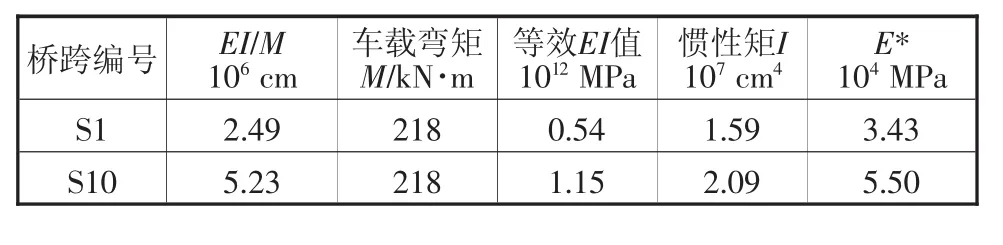
表4 20 m各跨等效EI与E*表

3 阈值分析与安全评估

桥梁监测阈值可视为桥梁性能的富余量值，管理值可以设定不同的安全标准作为不同的警戒线，桥梁的性能越好则量值越大。桥梁的监测管理阈值会动态改变，即随着时间的影响，桥梁会越老旧，梁底应力会趋渐接近危险界线，桥梁的性能富余量值也会渐渐变小，因此桥梁的监测管理阈值会因为劣化的程度而有所改变。

3.1 桥梁现状安全评估

利用修正的数值模型推估的各桥跨的梁底应力，可进一步评估桥梁现状的安全性。目前表5和表6的梁底应力仅考虑静载的影响，若要准确地评估桥梁现况的安全性，则需要加上设计活载观察应力是否会到达临界危险值。根据资料，40 m桥跨的设计活载重会对梁底产生3.99 MPa的拉应力，而20 m桥跨的设计活载重则会对梁底产生5.33 MPa的拉应力。

表5 40 m各跨静载重与活载重作用下的梁底总应力

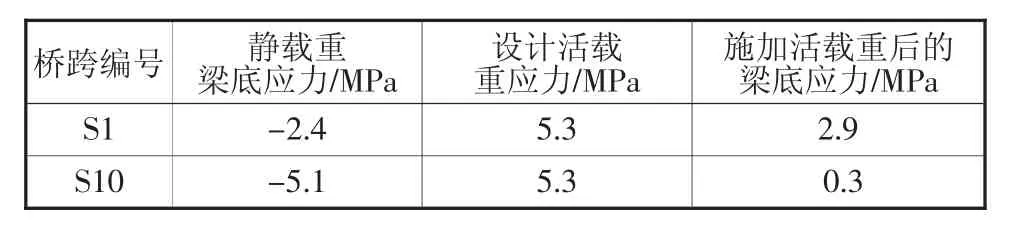
表6 20 m各跨静载重与活载重作用下的梁底总应力

考虑静载与活载交互作用下的梁底应力可进一步评估桥梁安全，将40 m桥跨设计活载造成的拉应力、梁底应力做加总，其值列于表5。20 m桥跨设计活载的拉应力与现状梁底应力做加总如表6，其中，负号代表压应力，正号代表拉应力。

由表中数据可知，其中可以发现多数桥跨梁底应力已经由压应力转变为拉应力。尤其是20 m桥跨，除了新建的第十跨外，其余拉应力皆超过了0.2 MPa，对于混凝土的桥梁结构来说，一旦梁底由压应力转为拉应力，就是拉起警戒线的时刻，因为混凝土本身受压不受拉，一旦超过拉应力的安全范围，混凝土即会产生裂缝，对整体结构造成安全上的影响[5]。由加总后的梁底应力来看，大多数桥跨目前确实有安全上的隐患，仔细考虑后建议进行持续性的监测管理，再决定是否要对桥跨进行加固或重建。

3.2 应变阈值分析

对于迈入中老年期的桥梁来说，利用监测数据建立管理值，可预防结构发生损坏。本文用以预力混凝土桥梁底部产生0.6倍容许拉应力为基准，将推算的现状应力与管理阈值做差异比较，现状应力因受到预应力的影响均为压应力，当预应力损失持续发生直至梁底应力达到容许拉应力时，其差值即为容许应力值。在Midas Civil中外力对模型造成的应力、变形等反应皆是利用线性迭加的概念来运作，因此可以利用线性关系去推算梁底应力达到容许拉应力的情况。将容许应力值除以弹性模量E即可得到应变容许值，由于梁底应力到达容许应力时，桥梁的使用性能将达到临界点，继续使用可能会发生混凝土开裂对结构造成永久性损坏，因此应变容许值可用来作为桥梁监测管理阈值的预警线，在结构损坏发生前提前预防。

40 m各跨监测管理阈值列表如表7，20 m各跨监测管理阈值列表如表8。

表7 40 m各跨监测管理阈值

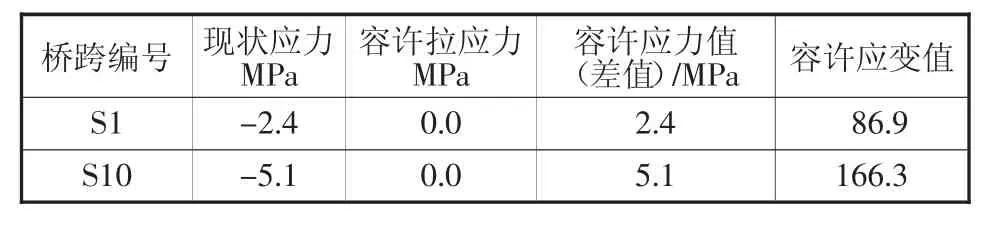
表8 20 m各跨监测管理阈值

4 结语

本文使用Midas Civil模拟预力混凝土I型梁桥老劣化的影响，利用各跨大梁中点梁底应力来做比较，并利用数值模型适当推估出监测管理值来保障桥梁的安全范围，得出以下结论：

a）模型是利用车载试验的结果进行弹性模量修正，但由表3和表4可以发现大多数桥跨等效弹性模量高于混凝土抗压强度35 MPa与混凝土抗压强度42 MPa的弹性模量，这是因为等效弹性模量包含了预应力的影响，因此在不改变断面惯性矩I值的情况下，等效弹性模量会高于一般的弹性模量。等效弹性模量会与监测应变数据有一定的关联，当挠曲刚度越大时表示桥梁越不容易产生应变。

b）仅考虑静载重情况下桥跨梁底应力皆维持在压应力范围，但加上设计活载重后，桥跨梁底应力多半落在拉应力范围，有安全上的隐患。建议对桥梁进行长期监测，决策是否需要进行加固或重建。