防爆门抗爆性能数值分析

供稿|刘季冬，明瑞，李湾，凌增光，明兴祖,4

内容导读

矿用防爆耐压密闭门(简称防爆门)是矿井作业规避事故的重要安全装备。本文根据防爆门的设计要求及结构模型建立了有限元仿真分析模型，采用显式非线性动力分析方法在三角形冲击波波峰压力0.6，1.0 MPa作用下仿真分析了防爆门整体和内部结构的应力、等效塑性应变、位移等抗爆性能响应。仿真分析表明：防爆门的联接零件间无塑性变形；门体结构出现的最大应力为339.3 MPa，最大变形量为3.461 mm；抗冲击强度足够；没有产生局部断裂、裂缝等破坏形式；防爆门的各零件的联接位置的位移变化小于1 mm；门体的密封性能良好；符合防爆门的刚度需求。防爆门的结构仿真模型和数值分析为提高煤矿井下防爆门的抗爆性能提供了理论指导。

煤矿井下作业经常发生瓦斯、煤尘爆炸，产生大量一氧化碳等有毒气体，直接造成安全事故[1]。矿用防爆耐压密闭门(简称防爆门)是规避事故的重要安全装备，其抗爆性能已成为煤矿井下生产装备的研究热点之一，对提升我国煤矿安全生产保障水平等具有重要意义[2]。

在抗爆性能研究方面，Katherine A[3]提出了一种分析救生舱的抗爆性能的数值计算方法，通过将爆炸的动载荷转化为静载荷的方式，均匀加载到救生舱的舱体上，并进行舱体结构的抗爆性能研究。Houf W G等[4]深入研究了瓦斯爆炸后舱体的变形情况，揭示了在瓦斯冲击波作用下舱体的变形规律。刘建英等[5]将泡沫铝夹芯板材料作为舱门，通过加强筋的固定作用强化舱体，通过数值计算了移动式救生舱的强度要求与安全系数。宋胜伟等[6]采用ANSYS仿真软件模拟舱体内的自动隔离门不同外界环境下的应力应变情况。吴广明等[7]通过LS-DYNA有限元软件仿真研究了舱室内在爆载荷作用下铺设凯夫拉防护材料发生的动态响应规律，建立了动态响应的有限元模型及舰艇舱室结构模型。王文娟等[8]在有限元方法的基础上通过结构动力分析的方式系统研究了煤矿的避难硐室中的密闭门在爆炸载荷作用下的受力及变形情况。

本文针对防爆门的设计和结构模型，采用显式非线性动力分析方法，通过建立有限元仿真模型，数值分析防爆门抗爆性能响应。

防爆门的设计要求及结构模型

在实际应用中，防爆门采用一种整体式的应用结构，门体为密闭式，防爆门的门体结构如图1所示。防爆门的门体为矩形结构，宽1120 mm，高2120 mm；防爆门的铰链联接板是门体的联接零件，长60 mm，厚225 mm；防爆门的门扇厚约200 mm，并且门扇的边缘安装有耐高温的密封条；防爆门门体的内腔尺寸约为1000 mm×2000 mm，防爆门门体的内腔四角具有圆形外观；加强筋是防爆门上关键的固定件，排布在门体的门扇内腔中。防爆门的主要联接材料是Q345钢，门体结构主要由Q345钢的扁条焊接而成，门体中间及门框均采用Q345钢的扁条联接。

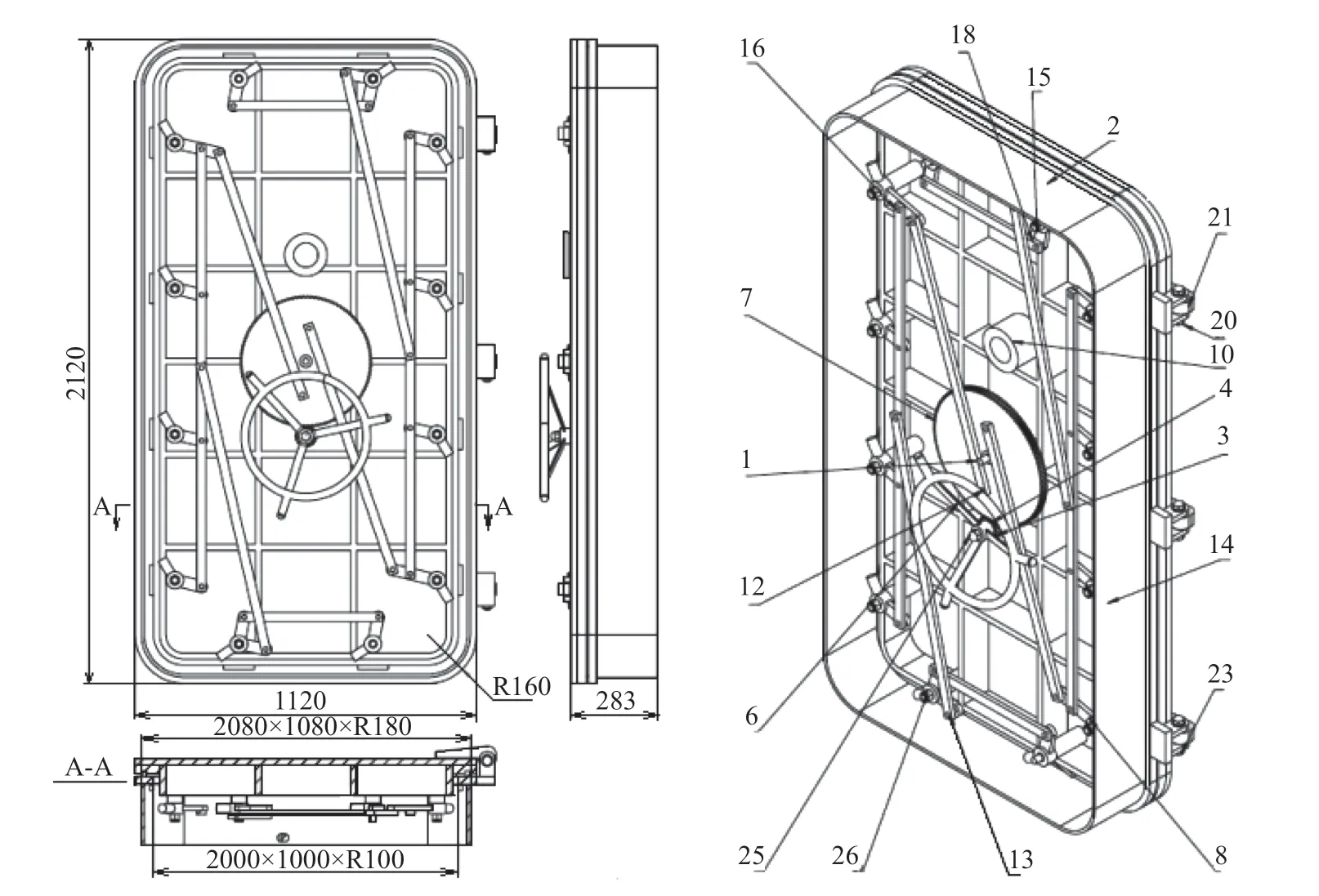
图1 防爆门的整体式结构(单位，mm)

防爆门主要零件的材料均采用Q345钢，如铰链、加强筋、大齿轮、手轮结构、盖板结构、门板焊件等零件；防爆门传动结构采用Q235钢来保证部件的刚性及稳定性；门体中的把手结构采用ZG45；门体中主要零件的联接部件，如螺母、螺栓、销钉、垫片、钢盖、螺母等均使用材料304不锈钢；通过铆钉铆接304不锈钢表面拉丝板作为外观门板；防爆门的观察结构采用高强度的防爆抗压玻璃；防火材料为MT113隔离抗静电的胶条材料。建立防爆门的三维模型如图2所示。在防爆门实际加工过程中，通过门栓将门框固定起来，门框通过铰链来联接，因此在数值仿真中将防爆门设定为固定约束[9]。

防爆门需要拥有一定的抗爆压力才能满足防护需求，至少能够承受0.6 MPa的压力，并且能够承受瓦斯爆炸产生的三角冲击波压力300 ms，其中防爆门的整体结构及关键部位承受的最大三角形冲击波压力为1 MPa。

图2 防爆门结构模型

有限元仿真分析模型

防爆门的数值仿真分析主要考虑爆炸冲击波作用的外界条件引起门体结构的应力破坏及应变变形。防爆门门体的位移变形是非线性变化的，因此在数值仿真中采用ANSYS软件中的显式非线性动力模块——LS-DYNA分析模块来进行分析，研究防爆门在爆炸环境下的变形情况及抗爆性能。

仿真模型

单元类型的选择

为了提高防爆门抗爆性能的模拟准确性与理论计算求解的正确性，需要根据防爆门的实际尺寸进行建模，对防爆门主体结构进行网格划分的同时，需要合理简化门体的一些部件，便于研究防爆门在爆炸冲击波下的形变情况，这便需要对仿真的单元类型进行合理选择[11]。考虑到防爆门的结构及计算需求，在ANSYS软件的模块程序LS-DYNA中，选择实体单元与弹簧阻尼单元作为仿真单元类型。在单元类型的选择中，主要针对防爆门的门体结构进行仿真处理，采用软件中的SOLID 164实体单元对门体结构进行整体的网格划分，采用软件中的COMBI 165弹簧阻尼单元对门体的销钉、螺栓等联接处进行局部的网格划分。

仿真网格划分

防爆门门体的结构特征较为复杂，需要对不同的表征参数进行多次实验研究，数值仿真也需要更精细的参数设置，本次仿真的网格划分参数如下：门体的划分的最大单元为25 mm，门体上零件联接处的细节部分划分的最大单元为15 mm，其比例系数设定为默认的参数1。设置好仿真参数后，对门体进行网格划分，划分的单元共135766个，如图3所示。

图3 防爆门数值仿真的网格划分示意图

材料关系模型与特性参数

防爆门在冲击波作用下会产生弹塑性变形。对防爆门材料而言，重点是考虑与稳定有关的弹塑性本构模型及材料的应变率，有限元分析时选用LSDYNA中材料模型Johnson-Cook[12]。

根据防爆门设计中各零部件的材料选择，防爆门的主要材料为Q345钢、Q235钢、ZG45钢等，材料的特征参数如表1所示。

表1 防爆门各零部件材料特性参数

仿真的边界条件及初始条件

防爆门的结构较为稳定，不存在相对松动的零部件，设定防爆门的初始条件下稳定可靠。门体各结构中没有焊接应力存在，焊接部位对门体结构无影响；防爆门各零件间没有安装变形，螺栓等联接件的预应力不影响门体结构特征。

边界条件

设定防爆门在承受爆炸条件下的冲击波时，冲击波的冲击压力直接作用于迎爆面上，门框上的铰链及其他零部件没有过定义接触情况的发生，在模拟条件下，设定门栓、门框固定，门框边界无其他压力作用效果，防爆门可以简化成固定约束，在仿真模拟条件下，通过ANSYS软件对防爆门的边界施加固定约束。

初始条件

通过防爆门的结构模型可知，门体的整体结构受到爆炸冲击波后，防爆门接触冲击波的外边界区域发生了弹塑性变形，变形的区域相对防爆门的整体结构幅度非常小，对网格划分的精度无明显影响。数值仿真选择拉格朗日算法，该方法能够直观处理物质界面并能精确描述材料边界与物质之间的相互关系[13]。

防爆门在爆炸环境的作用下可能会受到冲击波的直接破坏，为了减小误差，在数值仿真中将防爆门的正面作为迎爆面，并将峰值冲击波加载到迎爆面上，考虑到爆炸环境的安全系数及误差，本次仿真爆炸冲击波的最小峰值压力为0.6 MPa，数值计算中将冲击波的最大峰值压力为1.0 MPa，冲击波压力与时间的关系曲线如图4所示。

图4 防爆门所受冲击波压力与时间的关系曲线

防爆门整体结构数值分析

当爆炸冲击波作用在门体结构上时，设定门体结构所受的冲击压力持续300 ms，防爆门的压力峰值为0.6, 1 MPa，仿真中的计算时间为400 ms。通过ANSYS/LS-DYNA进行仿真分析，通过数值仿真分析防爆门结构所受的应力、应变情况，由仿真图中的应力、应变云图体现。为了保证防爆门良好的刚性结构，梁柱的最大变形量不能超过10 mm，即所受应力小于屈服应力。为防止密封失效，有密封要求的联接件相对位移应小于1 mm。

防爆门整体应力分析

根据防爆门整体网格划分，仿真计算后提取应力结果，如图5所示。当迎爆面的峰值压力达到0.6,1 MPa时，防爆门受到的应力最大值主要出现在门体的各联接位置，计算时间为350 ms时，迎爆面所受的冲击压力达到了339.3 MPa。可见，在冲击波持续300 ms的时间内，门体结构承受了两种载荷与冲击波的压力。从图中可知，门体结构所受应力没有超过材料的屈服极限，符合材料的强度需求。

等效塑性应变分析

防爆门门体在两种外界载荷的作用下，门体加强筋部分第38332单元及第150343单元应力达到了最大值，应力的变化曲线如图6所示。

塑性应变最大值出现在最后时刻，提取该时刻在波峰为0.6, 1.0 MPa两种载荷下塑性应变云图如图7所示，防爆门门体整体未出现塑性应变。

门体位移情况分析

防爆门的门体位移形变情况如图8所示，当门体在0.6, 1 MPa载荷的作用下，位移形变的峰值出现在防爆门的中间区域位置，位移变形量峰值分别达到1.706, 3.461 mm。可见，防爆门在承受波峰为0.6, 1.0 MPa，持续300 ms三角形冲击波时，防爆门的门体的最大位移变形量不超过10 mm。对其进行可靠性分析，防爆门各零件无裂缝及破坏现象产生，符合防爆门的刚性要求，能够保证防爆门安全的防护性能。

由防爆门整体位移场分析可知，防爆门的位移变形量最大时刻门体最大位移值在第13588、第23769两个节点处取得，分别提取两个节点处的位移与时间关系曲线即δ-t曲线，如图9所示。

图5 防爆门整体应力场

防爆门门板联接处的密封位置设置有3 mm厚的密封条，当防爆门在作用时间300 ms内所受的冲击压力峰值为0.6 MPa时，防爆门显著点的位移变化如图10所示。可以看出，防爆门上的联接零部件的最大位移变化数值为0.02 mm，出现在防爆门侧方中部的联接位置处。防爆门门板联接处的密封位置最大位移未超出1 mm，因此不会发生密封失效。

图6 防爆门应力达到最大值单元σ-t曲线

图7 门体结构的塑性应变场变化

图8 防爆门整体位移场

当防爆门门体在300 ms的作用时间内所承受的冲击压力峰值为1.0 MPa，提取门体各联接零部件显著点的相对位移数据(绝对值)如表2所示。联接件的相对位移最大值为0.004 mm出现在防爆门顶边中间位置的联接处，未超出1 mm，因此也不会发生密封失效。

防爆门内腔结构数值分析

防爆门内腔结构应力分析

在0.6, 1.0 MPa两种波峰载荷下，防爆门门体所受的最大应力发生在门体中间加强筋联接区域。当冲击压力持续时间达到70 ms时，最大应力达到169.6 MPa；持续时间达到210 ms时的最大应力为339.3 MPa。可见防爆门在承受两种载荷持续300 ms的三角形冲击波压力下，应力未超过材料屈服强度，能满足强度要求。

防爆门内腔结构位移分析

在0.6, 1.0 MPa两种波峰载荷下，防爆门腔内零部件的结构位移形变如图11所示，门体腔内零件结构的中间区域位置的位移变化达到了最大值。作用时间在70 ms时，位移变化达到了1.706 mm，作用时间在210 ms时，位移变化达到了3.461 mm。从图中可知，当波峰载荷为0.6 MPa时，防爆门腔内零件结构的位移变形范围在0～1.706 mm；当波峰载荷为1 MPa时，防爆门腔内零件结构的位移变形范围在0～3.461 mm，门体的内腔结构位移变化小于10 mm，没有出现破坏现象，符合材料的强度需求。当爆炸冲击压力作用在防爆门的门体结构上时，门体的位移变形极小，门体的密封性能不受其影响，不影响防爆门安全的使用性能，内部结构不会发生破坏失效，满足所需的刚度要求。

防爆门抗爆性能数值分析结果

防爆门在抗爆冲击波最大超压峰值为0.6, 1.0 MPa载荷下，数值仿真分析统计结果如表3所示。

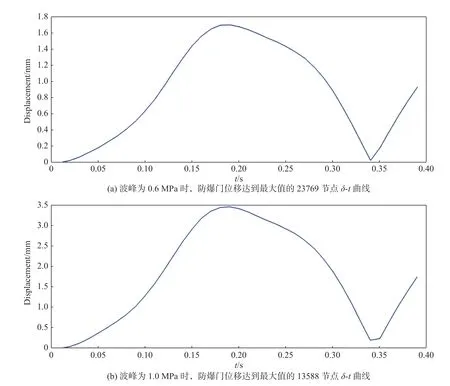
图9 防爆门整体位移达到最大值的节点位置δ-t曲线

根据表3，冲击波波峰压力为0.6 MPa防爆门整体结构所受应力的最大值为169.6 MPa，对应的位移变形量的最大值为1.706 mm，门体结构腔内联接区域最大变化位移发生在门体侧边中间位置，最大变化位移为0.002 mm；冲击波波峰压力为1 MPa下防爆门整体结构所受应力的最大值为339.3 MPa，对应的位移变形量的最大值为3.461 mm，门体内腔结构联接部件的最大变化位移发生在加强筋与门板的联接处，最大变化位移为0.004 mm。

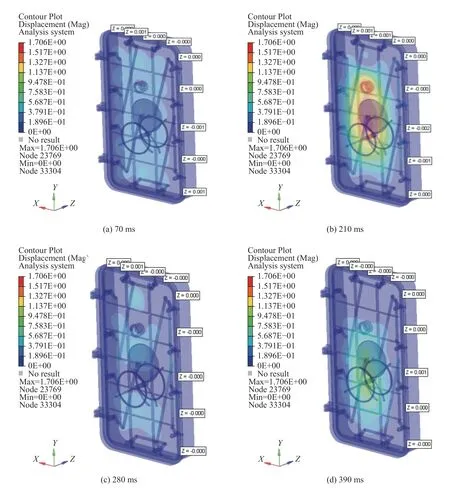
图10 冲击压力峰值为0.6 MPa防爆门显著点的位移变化

结束语

利用显式非线性动力分析方法，通过仿真分析得出：防爆门的整体结构与腔内结构所承受的冲击压力在材料的屈服强度之内，符合材料的抗压性能的要求；门体门板及加强筋零部件没有出现塑性变形等情况，最大位移变形量不超过10 mm，没有出现零件结构失效、断裂等破坏形式，符合防爆材料的刚度要求；防爆门中各零部件的相对位移变化小于1 mm，说明防爆门的密闭性能较好；防爆门无失效零部件，能够保持完整，结构强度和刚度达到安全要求。在煤矿井下实际应用中防爆门抗爆性能良好，说明防爆门结构模型和仿真数值分析有效可靠。

表2 冲击压力波峰为1.0 MPa防爆门联接零部件显著点相对位移数据表

图11 防爆门内腔结构位移场

表3 防爆门数值分析统计结果