一种基于MH改进的重启随机游走链路预测算法

吕 亮，何 敏，易 灿

(云南大学 信息学院，云南 昆明 650500)

当今社会，复杂网络无处不在[1]. 网络由节点和连边构成：节点表示不同的事物；连边表示事物间的联系，即事物间的链路关系. 链路预测可以帮助学者们分析复杂网络中事物间的联接关系，因而得到了广泛的研究[2].

链路预测是网络科学和机器学习的基础[3]，也是数据分析中一个重要的研究课题[4]. 链路预测对复杂网络中潜在的或未被发现的链接进行预测[5]，具有重要的理论价值和实际意义[6]. 在现实生活中，链路预测有着广泛的应用，例如好友推荐[7]、网络重构[8]、社区发现[9]等. 在解释网络演化的过程中，链路预测也起着重要作用[10]. 因此，如何提高链路预测的准确性，成为研究复杂网络的核心内容之一. 基本的链路预测算法分为两大类：一是基于节点相似性指标[11]，二是基于机器学习算法[12].

基于节点相似性指标的链路预测算法简单、实用，一直是研究的热点. 相似性理论认为，网络中两个节点的结构特征越相似，它们之间产生链接的可能性越大[13]. 近年来，机器学习算法的性能大幅提升，学者们将其引入链路预测以提高预测效果.其中，网络表示学习 (Network Presentation Learning，NPL)算法被大量应用[14]. Mikolov等[15]提出的神经网络模型Word2vec在词嵌入向量中取得良好效果；Perozzi等[16]提出的DeepWalk模型，利用随机游走 (Random Walk，RW)进行采样，结合Word2vec模型，得到节点的向量表示，效果显著. Gjoka等[17]借鉴MH (Metropolis-Hasting)算法，改变RW等概率采样邻居节点的策略，提出无偏采样算法(Metropolis-Hasting Random Walk，MHRW)，其采样的样本集更能全面的表达原始网络的结构特征[18-19]. 王文涛等[20]基于MHRW算法，删除自环率，设计出RLP-MHRW(Remove self-Loop Probability for MHRW)算法，提高了NLP的表示性能. 刘思等[21]利用DeepWalk模型，通过将节点表征到低维向量空间获得节点的潜在相似性来进行链路预测. Jin等[22]提出有扩展和监督的重启随机游走 (Random Walk with Restart，RWR)算法，使随机游走更具表现性，并将其应用于排序和链路预测. 吕亚楠等[23]考虑节点度值对粒子转移概率的影响，提出有偏向的链路预测算法，提升了预测的AUC指标.

基本随机游走相似性指标仅考虑当前节点的度对转移概率的影响而忽略了邻居节点的贡献，影响链路预测效果. 因此，本文在MH的基础上，提出一种改进的重启随机游走链路预测算法 (Improved MH with RWR，IMRWR). 算法在定义节点间的转移概率时，综合考虑当前节点及其邻居节点的度对转移概率的影响，并将节点的自环率按邻居节点的度值加权分配给邻居节点，以增大游走粒子转移到与其更加相似的节点上的概率，从而获得相似节点的随机游走序列，提高预测的准确性.

1 相关工作

1.1 链路预测问题描述设网络G=(V,E) 表示无向图，其中V={v1,v2,···,vN}表示节点集合，E={ei1,j1,ei2,j2,···,eiH,jH}表示连边集合，网络中不允许有自连边和重边. 节点vi,vj∈V间的连边记为(vi,vj)或eij，节点vi的邻居节点集合记为Γ(i)，记ki为节点vi的度. 如图1所示，V={1,2,3,4,5}，E={(1,2),(2,3),(3,4),(3,5),(4,5)}，Γ(3)=(2,4,5)，k3=3. 在进行链路预测实验时，连边集合E将被划分成训练集ET和测试集EP两部分，有E=ET∪EP，ET∩EP=∅，同时，由节点对构成的连边 (vi,vj) 将被赋予一个分数值sij.

图1 简单网络示意图Fig. 1 The diagrammatic graph of a simple network

在自然语言处理 (Natural Language Processing，NLP)中[24]，用邻接矩阵A来表示并存储网络G，A为N×N的非零对称矩阵，其中，元素ai j定义为

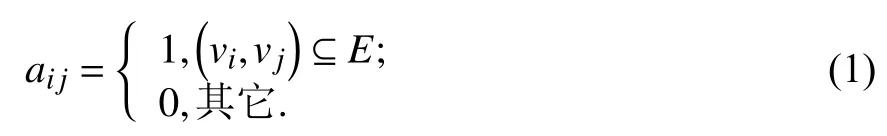
假定：①U为网络中N个节点互连构成的边集合，则U中有 (N(N-1))/2 条边；②B为不存在边集，有B∈U，B∉E；③W为未知边集，有W∈U，W∉ET且W=B∪EP. 由 图1得，U={(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)}，B={(1,3),(1,4),(1,5),(2,4),(2,5)}，链路预测即预测B中的边未来会出现的概率大小. 图2所示为边集U,E,B,W,ET,EP的关系维恩图.

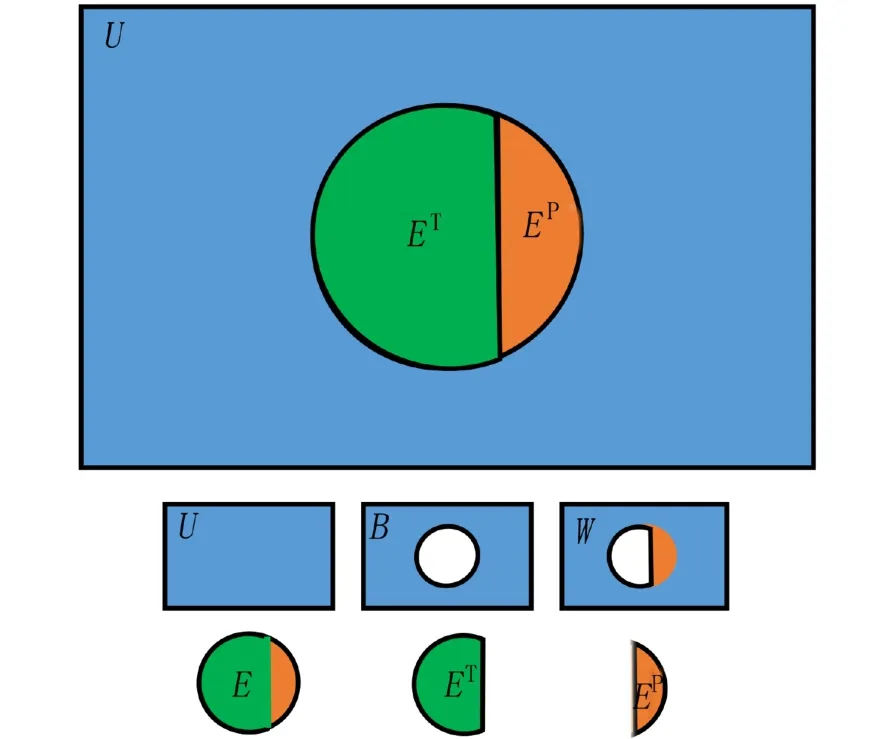
图2 边集维恩图Fig. 2 Venn diagram of edge set

1.2 RWR算法RWR[25]属于基本的随机游走相似性指标，其假设游走粒子在每走一步时都按一定的概率返回初始节点. 设粒子随机选取下一个邻居节点进行游走的概率为c，则随机返回初始节点的概率为 1-c，可得到网络的转移概率矩阵P，其中元素pij定义为

若初始时刻，游走粒子在节点vi处，则在t+1时刻，该粒子到达网络中各节点的概率向量为

（3）式稳态解为

其中，ei为粒子在节点vi处的初始状态，其与I同为单位矩阵.

RWR相似性表达式为

其中，πi j为游走粒子从节点vi出发最终游走到节点vj的概率，πji表示反向概率.

由式(2)可知，在RWR方法中，游走粒子从节点vi转移到邻居节点vj的概率仅与当前节点vi的度有关.

2 基于改进MH的IMRWR

在MH的基础上，本文提出一种改进的算法IMRWR，同时考虑当前节点及其邻居节点的度对转移概率的影响，并将节点的自环率按邻居节点的度值加权分配给邻居节点，以增强转移过程中表示出的节点相似性，再融合重启随机游走RWR相似性指标进行链路预测.

2.1 MHRW算法基于MH算法的思想，Gjoka等结合RW提出无偏采样算法MHRW[18]，其定义节点间的转移概率rij为

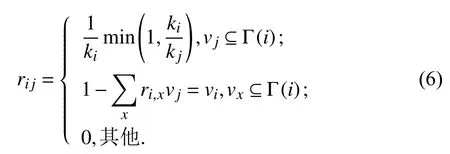
rij表示从节点vi到其邻居节点集合Γ(i)(包括自身节点)中选取节点vj进行采样的转移概率，当vj=vi时，表示继续采样当前节点.

2.2 IMRWR算法思想在图1的基础上，根据式(6)计算出节点间的转移概率，如图3所示，自环率rii表示采样当前节点的概率. 然而，节点v1仅有一个邻居v2，若从节点v1进行采样，下一个节点只能是v2，节点v1,v2间的转移概率应为r1,2=1. 但在MHRW中，节点v1的自环率高达0.5，自采样概率偏高，干扰了深度采样，从而影响游走粒子的转移过程.

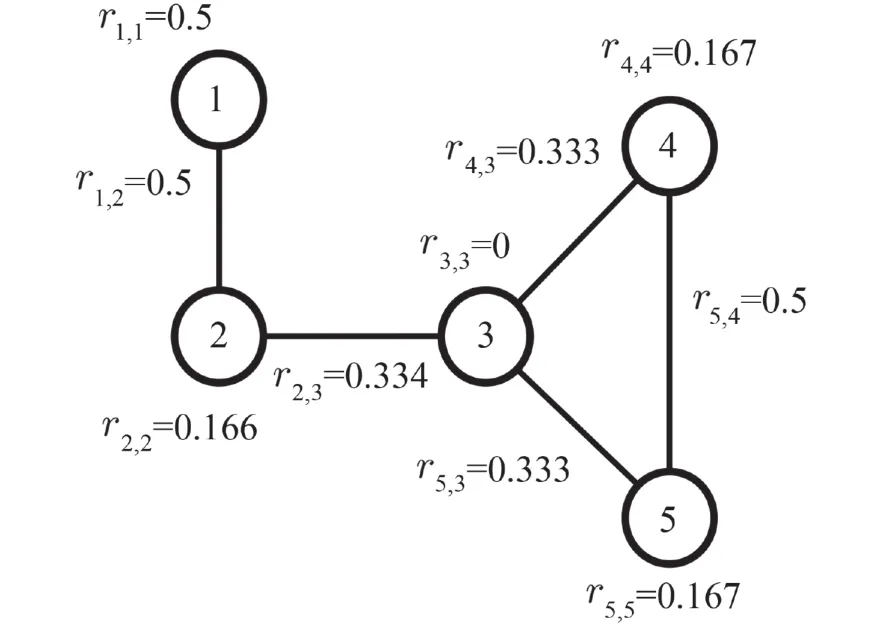
图3 MHRW转移概率图Fig. 3 The transition probability graph of MHRW

为充分利用邻居节点的度对网络节点间的转移概率的作用效果，同时消除自环率的不利影响，增加节点间的转移概率，使游走粒子能够转移到更加相似的节点上，以提高节点间的相似性. 本文利用MHRW算法，将当前节点的自环率按邻居节点的度值加权分配给邻居节点，则节点间的转移概率mi j为

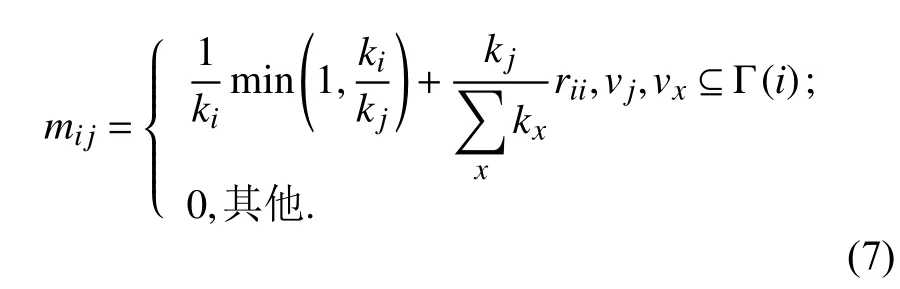
其中，rii由式(6)中当vi=vj时计算得到.

由式(7)可知，游走粒子在选取邻居节点进行游走时，既考虑当前节点的度，又考虑其邻居节点的度对转移概率的影响，同时除去了自环率，使游走粒子能够转移到网络的更深处寻找更加相似的节点. 如图4所示，从节点v1到v2的转移概率由原来的0.5提高到1，从节点v5到v3的转移概率由原来的0.333提高到0.433. 可见，本文IMRWR算法利用邻居节点的度信息增加了节点间的转移概率，使游走粒子转移到相似节点的概率增大.

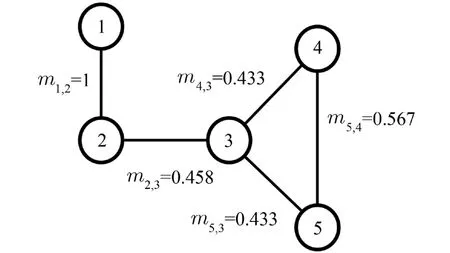
图4 IMRWR转移概率图Fig. 4 The transition probability graph of IMRWR

2.3 算法流程根据式(6)得到MHRW算法的网络转移概率矩阵R. MHRW算法步骤如下：

算法1MHRW算法

输入：网络的邻接矩阵，重启因子c

输出：节点间的相似性分数矩阵

步骤1初始化：i=1，转移矩阵R←0N×N，相似 性分数矩阵S←IN×N.

步骤2利用式(6)计算各节点与其邻居节点间的转移概率，得到网络的真实转移矩阵R.

步骤3若i＜=N，执行下一步；否，执行步骤6.

步骤4利用式计算节点vi与其他节点间的相似性分数值sij，并实时更新S.

步骤5判断S是否收敛，若不收敛，i++，执行步骤3；否则，执行步骤6.

步骤6输出S.

根据式(7)得到本文IMRWR算法的网络转移概率矩阵M. IMRWR算法步骤如下：

算法2IMRWR算法

输入：网络的邻接矩阵，重启因子c

输出：节点间的相似性分数矩阵

步骤1初始化：i=1，转移矩阵M←0N×N，相似性分数矩阵S←IN×N.

步骤2利用式(7)计算各节点与其邻居节点间的转移概率，得到网络的真实转移矩阵M.

步骤3若i＜=N，执行下一步；否，执行步骤6.

步骤4利用式计算节点vi与其他节点间的相似性分数值sij，并实时更新S.

步骤5判断S是否收敛，若不收敛，i++，执行步骤3；否则，执行步骤6.

步骤6输出S.

2.4 S 收敛性证明(1)因为转移矩阵R、M均为非负矩阵，游走粒子可以转移到网络G的任意节点，0＜c＜1，则网络中任意两个节点vi,vj间的相似性分数sij都能得到，所以R、M是不可约的；

(2)重启随机游走中，当游走粒子转移到某一节点后，能否再次转移到该节点是不确定的，说明粒子的转移过程是非周期的；

(3)粒子转移到某一节点后返回初始节点，有可能在一定的步长内再次转移到该节点，但两次转移到同一节点的步长可能相同也可能不同，说明粒子的转移过程具有不确定性.

由以上3点可得，本文IMRWR算法是各态历经的[26]，说明本文算法收敛，所以S也收敛.

3 实验结果与分析

3.1 实验基准方法前人已经提出了许多经典的相似性链路预测算法，这些算法常作为基准方法与提出的新算法进行比较. 本文从3种类型的相似性指标中选取7种具有代表性的算法作为基准方法：①基于局部相似性的CN[27]，HPI[28]，AA[29]，PA[30]指标；②基于路径相似性的Katz[31]指标；③基于随机游走相似性的RWR[25]，ACT[32]指标.

(1) 共同邻居 (Common Neighbors，CN)指标CN指标为最基本的相似性指标，其相似性定义为两个节点间共同邻居的数目. 其相似性表达式为

(2) 大度节点有利 (Hub Promoted Index，HPI)指标 HPI指标是在CN指标的基础上，并考虑了两个相连节点度的影响. 其相似性表达式为

(3) AA(Adamic-Adar)指标 AA指标根据共同邻居节点的度为每对节点赋予一个权重值. 其相似性表达式为

(4) 优先链接 (Preferential Attachment，PA)指标 PA指标认为新链接的节点对[vi,vj] 间的连接概率正比于两个节点度的乘积. 其相似性表达式为

(5) 全局路径Katz指标 Katz指标考虑了网络的所有路径，其相似性表达式为

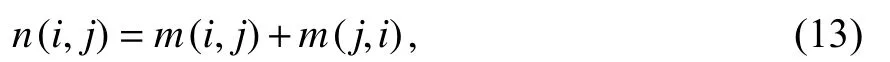
式中的数值解可通过该网络的拉普拉斯矩阵L的伪逆矩阵L+求得.

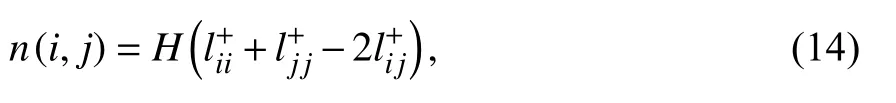
其相似性表达式为

其中，H为网络的总边数，表示矩阵L+中第i行j列的位置对应的元素.

3.2 实验评价指标验证链路预测算法准确性的评价指标主要有3种，分别是AUC、精确度(Precision)和排序分(Ranking Score). 这3种指标的侧重点不同，其中AUC指标能从整体上评价算法的准确性[33]，一直作为最主要的评价指标；精确度指标只计算预测前X条边中预测的准确率[34]；排序分指标只考虑测试边的最终排序情况[35]. 本文选取AUC和排序分两种评价指标作为评测依据.

(1) AUC指标 AUC指标定义为在测试集EP中随机选择一条边的分数值大于从不存在边集B中随机选择一条边的分数值的概率，随机比较n次，若有n′次分数值高，每高一次加1分，有n′′次分数值相等，每等一次加 0.5 分. AUC值定义为

AUC值在0～1之间，值越大的链路预测方法准确性越高. 若所有的分数sij都随机产生，AUC≈0.5.

(2) 排序分(Ranking Score)指标 排序分指标只考虑测试边e∈EP最终排列的位置，由1.1节定义可知，未知边集合为W，设re为测试边e在排序中的排名，则这条测试边的排序分定义为

遍历所有的测试边，得到整个系统的排序分指标为

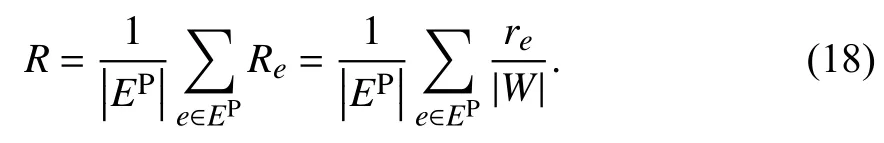
排序分指标与AUC指标不同，分数值越小预测越准确.

3.3 实验数据集本文选取了7个不同领域、不同规模且具代表性的真实网络数据集，这些数据集均为无向网络. 数据集包括美国航空网络(USAir)数据集、政治书籍网络(PolBooks)数据集和电子邮件网络(E-mail)数据集等. 7个数据集的网络结构特征如表1. 其中，N表示网络的节点数，H表示网络的边数，〈K〉表示网络的平均度，〈C〉 表示网络的平均聚集系数，D表示网络的相对直径. 由表1可知，在给出的数据集中，Karate、Dolphin 、PolBooks为相对小规模网络，C.elegens 、USAir 为相对中小规模网络，E-mail、PolBlogs为相对大规模网络.

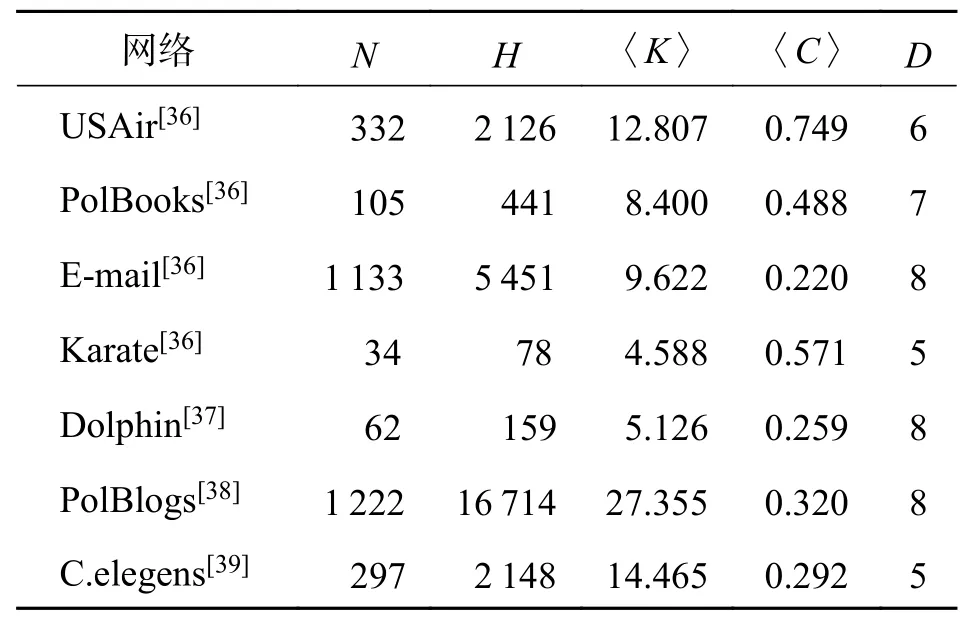
表1 各数据集的网络结构特征Tab. 1 Network structure features of each dataset

3.4 实验结果分析实验参数设置：重启因子c=0.85， 网络测试集划分比例 η=EP/E=10%. 每个数据集上独立重复实验 50 次，评价指标采用AUC和排序分，取平均值. 本文与7种基准方法比较了AUC指标，与MHRW、RWR算法比较了排序分指标. 实验结果如表2、表3及图5、图6所示. 表2比较了本文方法与各基准算法在7个数据集上预测结果的AUC值. 表3比较了IMRWR算法与MHRW、RWR算法在7个数据集上预测结果的排序分. 图5给出了同一类型的基准方法在7个数据集上预测结果的AUC直方图. 图6给出了本文方法与基准方法在7个数据集上预测结果的AUC折线图和排序分折线图.

由表2可知，与各基准方法相比，本文IMRWR算法在7个实验数据集上的AUC值均为最高，相较于MHRW算法也有提升. 由图5(a)知，在局部相似性指标CN、HPI、AA、PA中，AA指标不仅考虑了共同邻居，而且认为共同邻居中度小的节点对相似性的贡献更大，因此其在局部相似性指标中表现相对较好. 由图5(b)知，Katz为路径相似性指标，因此其在考虑路径的航空网络USAir数据集上的AUC值最高，若将它应用于路径的预测会有很好的效果. RWR、ACT均为随机游走相似性指标，其中，RWR表现最佳，与RWR算法相比，本文IMRWR算法在AUC指标上平均提升2.00%，最高提升可达3.98%. 同时，IMRWR算法在小规模数据集的AUC值提升比大于大规模数据集的提升比，说明本文算法更有利于改善小数据集链路预测效果，并且AUC值随着数据集规模增大而增大，说明本文算法对大规模数据集上的链路预测同样有效.

表2 在不同的基准方法下各数据集的 AUC 值Tab. 2 The AUC value of each data set under different benchmark methods

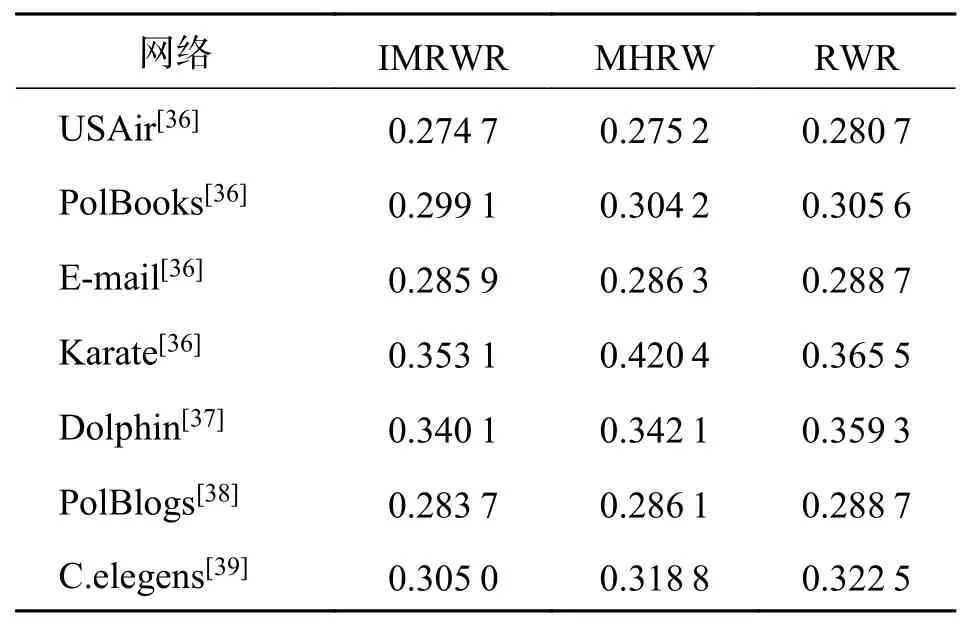
表3 各数据集在不同的基准方法下排序分值Tab. 3 The ranking score value of each data set under different benchmark methods

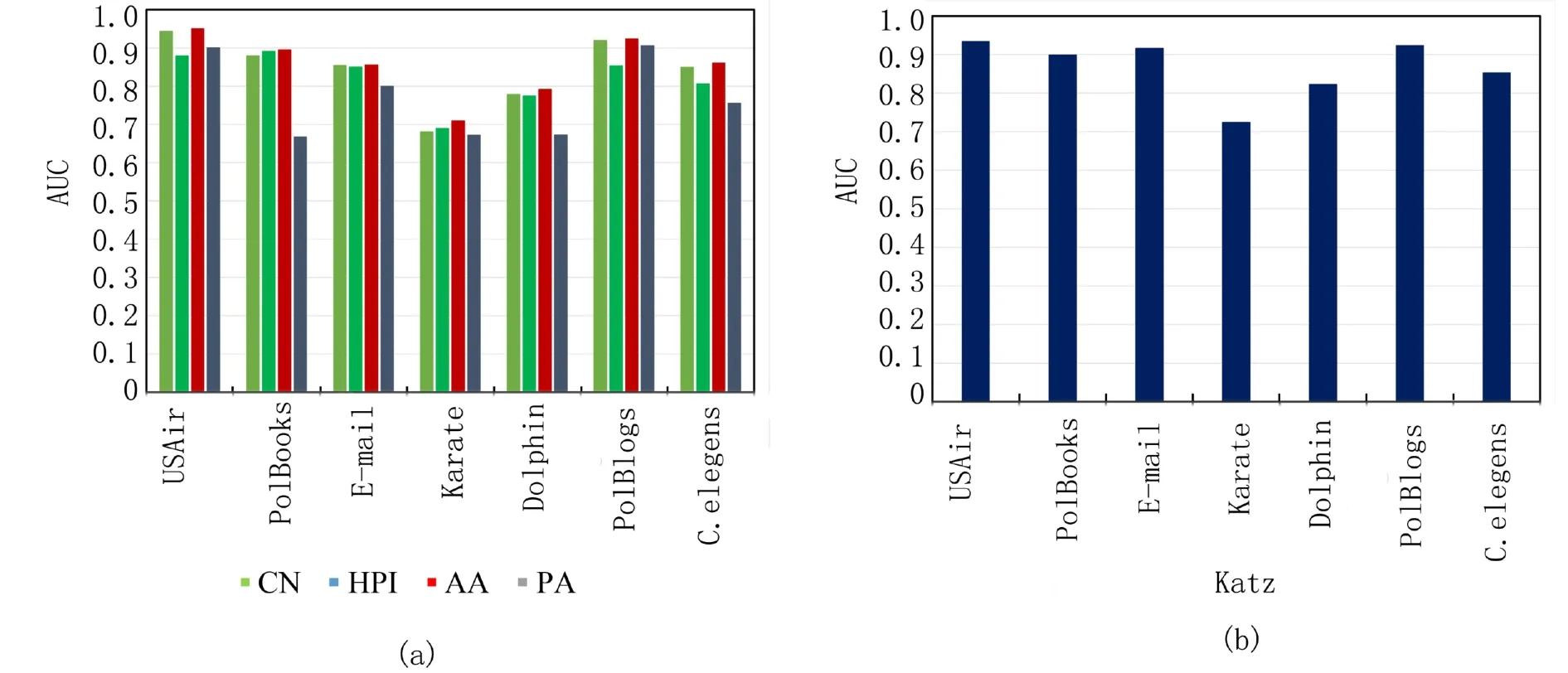
图5 局部相似性指标（a）与路径相似性指标（b）比较直方图Fig. 5 The comparison histogram of local similarity index (a) and path similarity index (b)

图6 AUC指标（a）与排序分指标（b）比较折线图Fig. 6 The comparison line chart of AUC index (a) and Ranking Score index (b)

由表3知，IMRWR算法在7个实验数据集上的排序分均比MHRW、RWR算法低，与RWR算法相比，平均下降0.99%，最高下降1.92%，也说明了IMRWR算法可提升预测准确性. 由图6(a)可知，同一算法在不同类型的数据集上AUC值波动明显，且同一数据集利用不同的预测方法得到的预测结果相差较大，说明不同的预测方法有着各自侧重的预测数据集. 而本文算法与其他算法相比，在7个数据集的AUC值波动相对平缓，说明本文算法有着更加稳定的预测性能. 且由图6(b)可知，IMRWR算法与RWR算法的预测结果走势基本相同，说明IMRWR算法有着一定的鲁棒性.

4 结束语

本文针对重启随机游走相似性指标忽略邻居节点的度对转移概率产生影响，提出一种改进MH的重启随机游走链路预测算法IMRWR. 该算法在定义网络节点间的转移概率时，综合考虑了当前节点和邻居节点的度对粒子转移过程的影响，并将自环率按邻居节点的度值加权分配给邻居节点，从而使游走粒子能够转移到更加相似的节点上，以提高随机游走获得的节点序列中各节点的相似性. 实验结果表明，本文所提算法在AUC指标和排序分指标上均有改善，在AUC指标上平均提升2.00%，最高提升3.98%；在排序分指标上平均下降0.99%，最高下降1.92%，提升了链路预测的准确性.下一步，我们将考虑结合边权值对转移概率的贡献，研究有权网络的链路预测性能.