基于排序多元Logit 模型的卡特尔类机组串谋竞价识别

2021-03-30邓瑞林谢敬东

电力系统自动化 2021年6期

孙波，邓瑞林，谢敬东，孙欣

（上海电力大学经济与管理学院，上海市200090）

0 引言

在电力现货市场的起步阶段，不排除市场成员存在市场力滥用行为。市场力滥用形式很多，发电商串谋为其中一种形式［1-2］，是指多家发电商结成“联盟”，通过“联盟”内部部分机组报高价的方式抬高市场出清价，从而获取超额利润。这种行为违背了市场公平交易规则。因此，防范发电商串谋行为的发生是保障市场健康运行的迫切需要，在市场报价阶段及时识别机组串谋竞价是其重要环节。

针对发电商串谋行为，文献［3］指出长期重复博弈、市场集中度高等是串谋形成的重要因素；文献［4］设计了防串谋机制；文献［5］介绍了串谋的缓解措施。这些文献考虑了机组串谋形成的因素、防串谋机制及缓解措施，但未对串谋行为进行识别。文献［6］对机组报价和容量进行分析，设计了识别机组串谋竞价的综合评判算法；文献［7］从交易前、中、后3 个维度构建了发电商串谋指标体系并识别串谋行为；文献［8］构建了基于云模型与模糊Petri 网的串谋行为综合评判方法。这些文献依据机组数据特征，通过构建评判指标识别串谋行为，但指标选取存在一定主观性，且未深入挖掘不同市场份额发电商机组报价的计量特征。文献［9-11］采用古诺模型、囚徒困境矩阵等博弈论模型对市场串谋行为进行了理论分析；文献［12］提出了一种基于雅可比矩阵的串谋行为识别方法。这些文献通过博弈论、雅可比矩阵等对串谋行为进行理论推导分析，但缺乏实践应用性。

Logit 模型是经典离散选择模型，可解决因变量为离散变量以及不同离散变量间差异性问题，该模型已被用于识别各领域市场成员的串谋行为。基于Logit 模型，在证券交易领域，文献［13］构建了股票信息型串谋行为识别模型；在工程招投标领域，文献［14］识别了公路合同的串谋投标；在制造领域，文献［15］对制造商的串谋行为进行了识别；在航空领域，文献［16］制定了针对串谋行为的2 个实证检验，验证了航空业存在串谋行为。排序多元Logit 模型是求解因变量为离散变量且为排序问题的方法［17］，机组报价排序为离散变量的排序问题，通过分析不同机组报价排序的差异，识别卡特尔类机组串谋竞价，为防范串谋行为的真正发生提供前期的监测预警。

本文基于排序多元Logit 模型，提出了一种识别卡特尔类机组串谋竞价的方法。首先，依据市场份额将机组分为卡特尔类机组和竞争类机组。其次，构建机组报价回归方程，并通过邹检验判断报价影响因素对2 类机组报价行为的影响程度是否存在差异。若存在差异，则建立卡特尔类机组报价的排序多元Logit 模型，利用似然比检验（LRT）判断卡特尔类机组的高价序列和低价序列之间是否存在差异，论证卡特尔类机组是否有串谋竞价的可能性。最后，将该方法应用于某地区现货市场中，对方法进行验证。

1 总体思路

市场份额是发电商市场力滥用的重要因素，因此根据市场份额对发电商进行分类。一类是市场份额多，有较强能力参与串谋竞价的发电商，称为卡特尔类发电商，其所拥有的机组称为卡特尔类机组；一类是市场份额少，较难参与串谋竞价的发电商，称为竞争类发电商，其所拥有的机组称为竞争类机组。由于串谋联盟的成员越多，联盟维系的难度越大［18］，且串谋成员往往是卡特尔类发电商［19］。因此，本文假设竞争类发电商不参与串谋竞价。

卡特尔类机组串谋竞价识别的总体思路如图1所示。

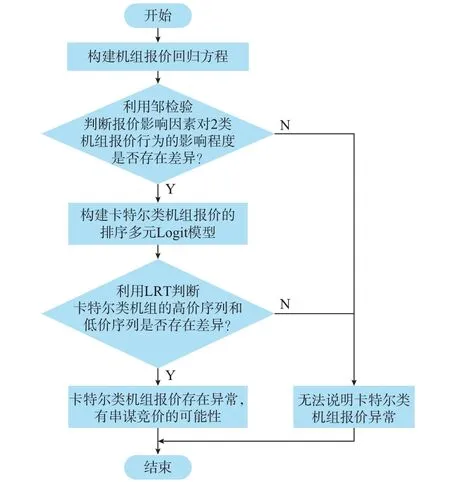
图1 卡特尔类机组串谋竞价识别的总体思路Fig.1 General idea of collusion bidding identification of Cartel-type generators

首先，基于计量经济学相关理论，并依托博弈论原理，构建机组报价回归方程。

其次，利用邹检验判断报价影响因素对2 类机组报价行为的影响程度是否存在差异。若接受原假设，说明不存在差异，则无法说明卡特尔类机组有异常；否则，需进一步分析卡特尔类机组的报价序列。

接着，选取卡特尔类机组最后一段报价作为机组报价，按由低到高进行排列，以平均值为分界点，大于平均值的报价序列为高价序列，小于平均值的报价序列为低价序列。针对卡特尔类机组高价和低价序列，分别构建排序多元Logit 模型并估计参数。

最后，利用LRT 判断卡特尔类机组高价序列和低价序列是否存在差异，若拒绝原假设，说明存在差异，则卡特尔类机组有串谋竞价的可能性；否则，无法说明卡特尔类机组报价存在异常。

2 机组报价行为差异性分析

2.1 机组报价回归方程的建立

电力市场中，机组报价交易是相互博弈的过程。参考文献［20］，假设每个机组仅知道自己的发电成本分布且机组属于完全理性的主体，则机组边际成本Ci，t为:

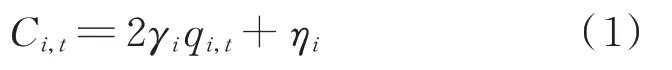
式中:γi和ηi为第i 个机组边际成本参数；qi，t为第i个机组在t 时刻的有功功率。

边际成本报价是机组占优策略。但实际竞价中，机组并非都是完全理性的主体，因此，可在边际成本报价上乘以报价策略系数变量。为简化模型，假设γi=0，即边际成本为常数，构建机组报价回归方程为:

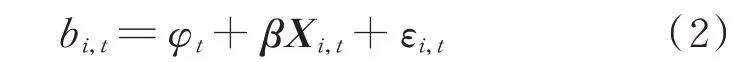
式中:bi，t为第i 个机组在t 时刻的报价；φt为电力市场交易的固定效应；Xi，t为影响第i 个机组在t 时刻报价的报价策略系数变量；β 为相应机组方程参数；εi，t为第i 个机组在t 时刻的随机误差项。

针对机组报价策略系数变量的影响因素，主要考虑机组的历史平均报价水平、已签合约量及市场供需比［21-22］，其他忽略不计。历史平均报价水平是指历史周期内机组报价平均值，已签合约量为机组已签中长期合约量分解到该时刻的合约量，市场供需比是指该时刻市场供应量和需求量的比值。

根据式（2）及影响因素，2 类机组报价回归方程分别为:

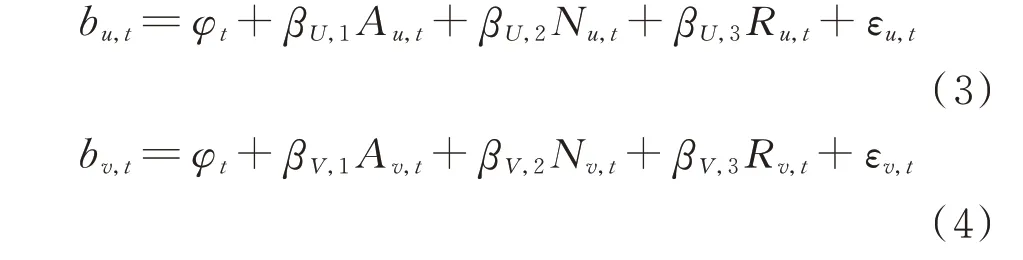
式中:bu，t，Au，t，Nu，t，Ru，t，εu，t分别为第u 个卡特尔类机组在t 时刻的报价、历史平均报价水平、已签合约量、市场供需比及随机误差项，其中u=1，2，…，U；βU，1，βU，2，βU，3为U 个卡特尔类机组方程参数；bv，t，Av，t，Nv，t，Rv，t，εv，t分别为第v 个竞争类机组在t 时刻的报价、历史平均报价水平、已签合约量、市场供需比及随机误差项，其中v=1，2，…，V；βV，1，βV，2，βV，3为V 个竞争类机组方程参数。

2.2 机组报价回归方程的验证

邹检验是测试2 组不同数据的线性回归参数是否相等的经典检验方法，参数的差异可以反映报价影响因素对2 类机组报价行为影响程度的差异。

邹检验原假设为H0:βU，1=βV，1，βU，2=βV，2，βU，3=βV，3，统计量W 为:

式中:EALL为所有机组报价回归方程的残差平方和；EU为卡特尔类机组报价回归方程的残差平方和；EV为竞争类机组报价回归方程的残差平方和；F(k，U+V-2k)表示自由度为(k，U+V-2k)的F 分布；k 为方程约束参数个数。

3 机组报价序列差异性分析

3.1 机组报价的排序多元Logit 模型的建立

串谋竞价往往是通过部分机组竞争性报价，部分机组报高价的方式。若卡特尔类机组串谋竞价，那么卡特尔类机组高价序列往往不是竞争性报价，低价序列是竞争性报价，即高价和低价序列的报价策略存在差异。竞争类机组均为竞争性报价，因此高价和低价序列的报价策略往往不存在差异。

根据机组报价回归方程和随机效用理论，当随机误差项εi，t采用极值分布时概率分布f 为:

式中:P 为概率；ξ 为εi，t任意取值。

定义ωi，t=φt+βXi，t，则bi，t概率分布为:

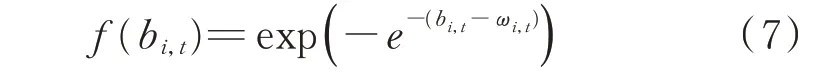
第i 个机组在t 时刻报价最低的概率［23］为:

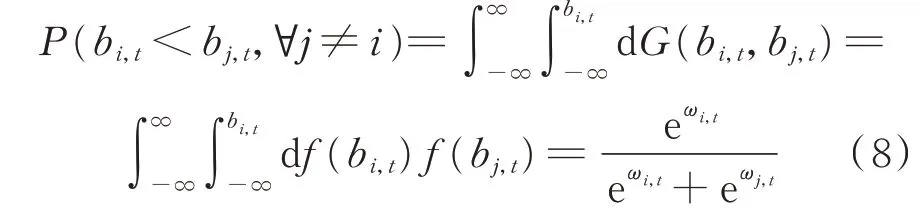
式中:G(bi，t，bj，t)为bi，t和bj，t的联合分布。

使用排序多元Logit 规范，t 时刻所有机组报价序列似然函数L(β)为:

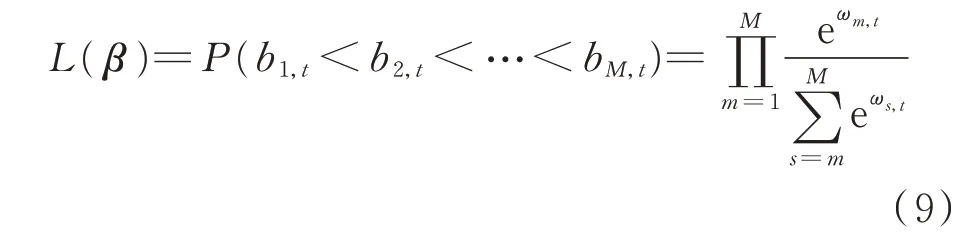
式中:m 和s 为机组报价序列的下标，且m=1，2，…，M，其中M 为总机组数。

所有机组T 个时刻报价序列对数似然函数ln L(β)为:

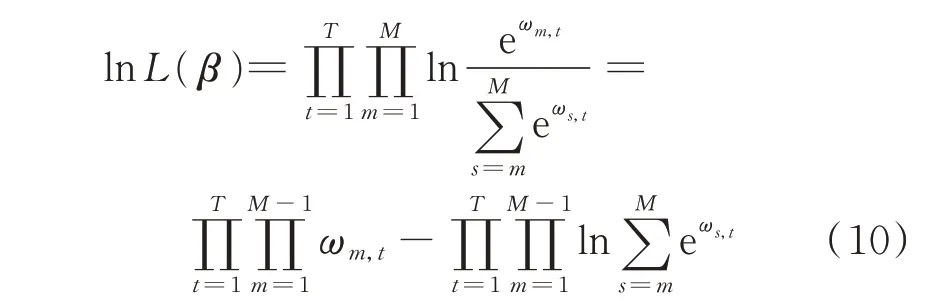
ln L(β)在β 中是全局凹的，因此对数似然函数有唯一最大值。

3.2 机组报价的排序多元Logit 模型的验证

将式（10）分解为机组高价序列概率和低价序列概率［24］，如式（11）所示。

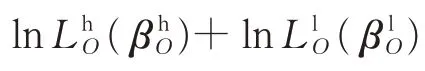
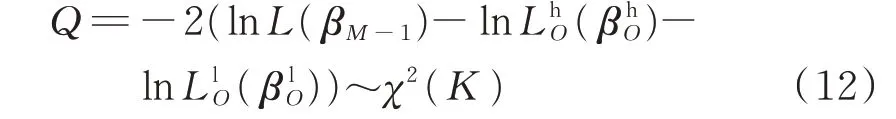
式中:χ2(K )表示自由度为K 的卡方分布；K 为模型约束参数个数。

假设在α 的显著性水平下，判断是否拒绝原假设，从而识别机组串谋竞价的可能性。

4 算例分析

4.1 数据选取

本文选取2006 年某地区电力市场现货数据进行研究，为国内即将开展的现货市场提供参考和借鉴。本文选取其中72 台机组为研究对象，以某日96 次报价为研究周期。机组报价、历史平均报价水平及市场供需比数据见附录A 图A1 至图A3。

前4 家发电商A、B、C、D 的市场份额如图2 所示。基于该地区实际情况，依据管制经济学中行业集中率指标等方法［25-26］，该地区为中下集中寡占型市场，因此可选取前4 家发电商为卡特尔类发电商，其拥有机组共21 台，其他竞争类发电商拥有机组共51 台。

图2 发电商的市场份额Fig.2 Market shares for power producers

4.2 报价行为差异性结果分析

为消除量纲和数值问题影响，对数据进行归一化处理，2 类机组报价分布和归一化数据分别如图3、图4、表1、表2 所示。

图3 竞争类机组报价分布Fig.3 Bidding distribution for competitive-type generators

图4 卡特尔类机组报价分布Fig.4 Bidding distribution for Cartel-type generators

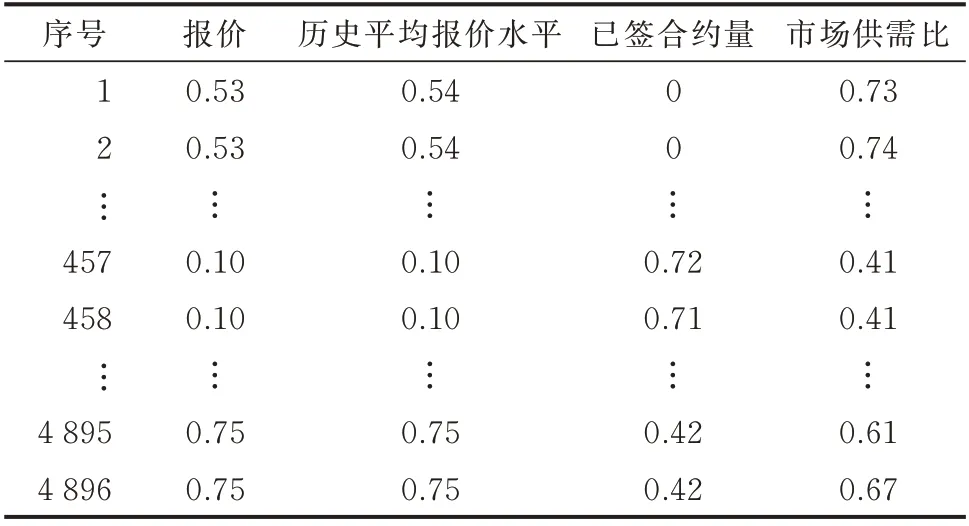
表1 竞争类机组归一化数据Table 1 Normalized data for competitive-type generators

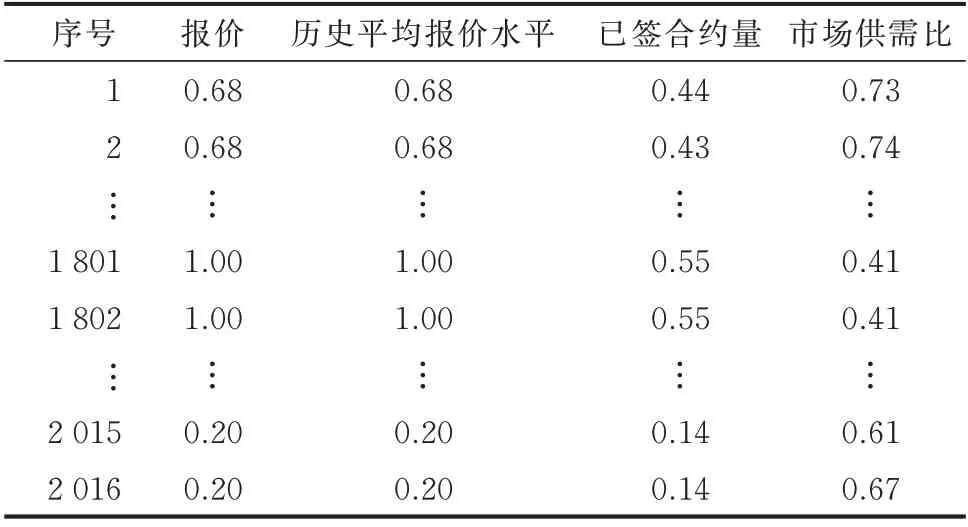
表2 卡特尔类机组归一化数据Table 2 Normalized data for Cartel-type generators

由图3 和图4 可知，与卡特尔类机组相比，竞争类机组报价水平整体偏低，卡特尔类机组报价呈现出2 种报价水平。比较表1 和表2 可知，卡特尔类机组的报价与历史平均报价水平相比有些竞争类机组低。

通过Eviews 软件，采用所有机组、51 台竞争类机组和21 台卡特尔类机组信息分别对方程进行估计，结果如表3 所示。

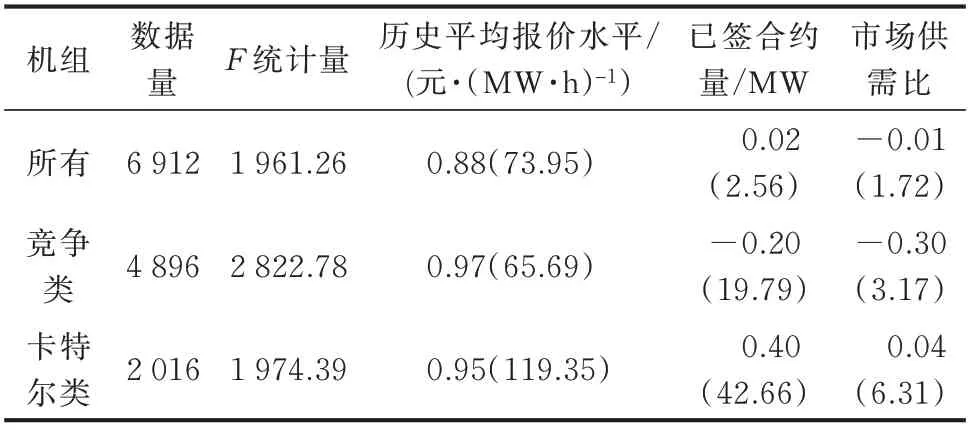
表3 机组报价回归方程估计结果Table 3 Estimation results of bidding regression equation of generators

由表3 中竞争类机组F 检验和t 检验结果可知，在5%的显著性水平下，竞争类机组报价回归方程和模型参数是显著的，估计值也是符合预期的。卡特尔类机组也有相同结论。

针对2 类机组方程参数进行邹检验，得到邹检验统计量为16.16，服从自由度为（3，6 906）的F 分布，概率值为0。因此，在5%的显著性水平下，拒绝了原假设，说明报价影响因素对2 类机组报价行为的影响程度存在差异，需进一步分析。

4.3 报价序列差异性结果分析

卡特尔类机组报价平均值为360 元/（MW·h），基于高价序列和低价序列分类原则，对机组进行分类。采用卡特尔类机组所有报价序列、低价序列及高价序列信息分别对模型进行估计，结果如表4所示。

表4 卡特尔类机组的排序多元Logit 模型估计结果Table 4 Estimation results of ordered Logit model for Cartel-type generators

由表4 中模型参数z 检验结果可知，在5%的显著性水平下，模型参数的估计是显著的。在模型参数相等的原假设下，根据式（12），可知LRT 统计量Q=9.96，服从自由度为3 的χ2分布。在5%的显著性水平下，拒绝了原假设，卡特尔类机组高价和低价序列之间存在差异，说明卡特尔类机组有串谋竞价的可能性。

低价序列的历史平均报价水平参数为正，说明历史平均报价水平越高，则机组报价越高；已签合约量和市场供需比参数为负，说明已签合约量越多、市场供需比越大，则机组的报价越低。历史平均报价水平、市场供需比参数较大，说明对机组报价影响较大，这也体现了历史平均报价水平、市场供需比对机组报价策略的影响及机组报价的稳定性。

高价序列的3 个参数均为正，说明历史平均报价水平越高、已签合约量越多、市场供需比越大，则机组报价越高。已签合约量参数最大，说明对机组报价影响最大，市场供需比参数最小，对机组报价影响最小，这也体现了机组是以抬高市场出清价为目的，而非竞争性报价。根据以上分析，进一步说明卡特尔类机组高价序列和低价序列报价策略的不同，这也是卡特尔类机组串谋竞价的方式。

4.4 方法有效性验证

为了验证方法有效性，由竞争类机组报价平均值330 元/（MW·h）对机组进行分类，并对模型进行估计，结果如表5 所示。

表5 竞争类机组的排序多元Logit 模型估计结果Table 5 Estimation results of ordered Logit model for competitive-type generators

由表5 中模型参数z 检验结果可知，在5%的显著性水平下，模型参数的估计是显著的。计算可知LRT 统计量Q=5.74，服从自由度为3 的χ2分布。在5%的显著性水平下，接受了原假设，说明竞争类机组高价和低价序列之间没有差异。

4.5 方法比较分析

美国部分成熟电力市场通常采用行为与影响测试方法，该方法具有应用直觉、简单、透明、易于被市场参与主体所接受等优点［27］。因此将该方法和本文方法进行比较，得出以下结论。

1）行为与影响测试方法需设定行为测试阈值，若阈值设置不合理，可能造成监管不足或过度。尤其在供需紧张时，机组往往会做出合理的报价上调行为，若阈值未适当调整，则会将该行为认定为市场力滥用行为。而本文方法不需要设定该类阈值，其通过比较高价与低价序列是否存在统计意义上的差异来识别，而高价和低价序列是由机组报价相对值确定，因此其确定过程不易受供需变动的影响。

2）行为与影响测试方法注重识别个体机组滥用市场力的情况，而本文方法注重识别多个机组串谋竞价的情况。