考虑网损与负荷偏差的节点边际电价模型与求解

张丙金，丁 恰，曹荣章，涂孟夫，张彦涛，冷 月

（1. 智能电网保护和运行控制国家重点实验室，江苏省南京市 211106；2. 南瑞集团有限公司（国网电力科学研究院有限公司），江苏省南京市 211106）

0 引言

节点边际电价（locational marginal price,LMP)定义为满足节点单位新增负荷需求时的系统边际成本，能反映电力供需的时空分布特性，是集中式电力市场普遍采用的定价方式，广泛运用于美国（PJM、ERCOT、CAISO）、欧洲、新西兰等电力市场。中国2015 年启动了新一轮电力市场改革，首批试点单位中广东、浙江、甘肃、山东等地均选择了LMP 作为现货市场的定价机制［1-3］。

LMP 的计算方法经历了不考虑网损的直流潮流模型、考虑网损的直流潮流模型、交流潮流模型几个阶段［4］。网损对电网中不同节点的LMP 影响很大，因此不考虑网损的LMP 模型主要用于对比分析［4］或研究新的算法［5］。基于交流潮流模型的计算方法由于存在局部最优解、计算效率等问题［6］，多作为研究中的参考基准值来比较不同方法计算结果的准确性［4，6-10］。因此，改进网损建模方法、缩小直流与交流算法的误差是LMP 研究的热点之一［6-9，11-13］。

考虑网损的直流优化模型建模分为2 种:一种是建立近似的网损计算模型，通常采用网损因子计算［7，11-12］或线性化的潮流方程计算［6，8］；另外一种是采用交直流迭代的方式，利用交流潮流计算网损，然后将其以固定数值的方式在LMP 模型中建模［9，13］。上述任意一种建模方式，节点负荷都必须是已知量。基于网损因子的计算模型，利用节点负荷建立系统平衡约束，LMP 采用系统平衡约束影子价格、网损因子、阻塞支路影子价格、直流灵敏度计算［7-9，11-13］；基于线性化潮流方程的计算模型，利用节点负荷建立节点功率平衡方程，LMP 为节点功率平衡约束的影子价格［6，8，14］。

发用电平衡是电力系统的基本特征，发电指所有发电机生产的功率，用电指所有用电负荷，电能在电网中传输产生的总损耗为系统网损。针对有功功率平衡问题，平衡方程可简单描述为“发电=用电+网损”。电力市场的目的之一是编制满足需求的机组计划、发现电力价格，出清依据的是申报或预测的用电负荷。已知用电负荷进行出清和LMP 计算时，用电负荷总和与系统网损之和等于发电计划总和。然而，中国在编制机组计划时，是同时预测发电总和（系统负荷）与节点负荷（母线负荷）［15-16］。由于系统负荷与母线负荷分别预测，二者预测对象和统计口径不同，且系统网损为未知量，因此系统负荷与母线负荷、系统网损之差亦是未知量，本文将该差值定义为负荷偏差。当已知系统负荷编制发电计划时，若不考虑系统网损，可以简单将负荷偏差以某种比例分配至所有节点，用修正后的节点负荷建模求解即可［5］；当考虑网损时上述分配方式将不可行，因为此时存在系统网损、负荷偏差2 个未知量。当前，新一轮电力市场改革正处于起步阶段，多家试点单位的市场规则明确规定“采用发电侧报价报量，以系统负荷预测为依据进行出清［1-3］”。

目前文献中尚未发现基于系统负荷出清和LMP 计算时可精确计算系统网损与负荷偏差的方法。本文就此展开研究，提出网损分布因子分摊系统网损与负荷偏差分配因子分摊负荷偏差相结合的方法，并建立2 种LMP 计算模型予以实现，算例仿真结果验证了该方法的有效性。此外，本文还构建了基于IEEE 14 节点和IEEE 118 节点模型的多场景算例，分析负荷偏差分配因子、负荷偏差水平对LMP 的影响。

1 考虑网损的LMP 计算

系统的有功功率平衡方程如式（1）所示，发电计划等于母线负荷与系统网损之和（本文将厂用电也视为母线负荷）。已知母线负荷编制发电计划时，只需要建立网损计算模型即可求解，网损估计模型的准确性决定了发电计划和市场价格信号的准确性。故而有大量文献聚焦在如何准确地估算系统网损。

式中:Pgen为发电计划总和；Pbusload为母线负荷总和；Ploss为系统网损。

基于网损因子的LMP 模型可将LMP 分解成能量分量、网损分量与阻塞分量［11］，常用于输电阻塞的管理，因而得到广泛应用。早期的模型是利用单平衡机潮流方法推导并计算网损因子，利用节点注入功率计算系统网损，并按照式（1）在系统平衡约束中计及网损［11］。考虑到网损因子计算的网损存在偏差，文献［13］提出了采用交直流迭代法精确估算系统网损，将交流潮流的网损值作为常数在系统平衡约束中建模。采用单平衡机的LMP 模型的缺点是LMP 的各分量与平衡机选择相关。随后，基于分散平衡节点的网损因子计算方法［17］和基于分散平衡节点的LMP 计算方法被提出［18-19］，并有文献研究基于分散平衡节点的阻塞管理［20］，然而此类方法也面临着平衡机功率分配系数的决策难题。

文献［12］指出采用单平衡节点或分散平衡节点计算的网损值虽然相同，但是平衡节点的选择会影响线路潮流，从而影响模型的解与LMP。因此，文献［12］改进了LMP 分解模型，利用网损分布因子将网损分摊至节点，改进后的模型不仅网损不变，而且参考节点的选择将不再影响模型的解与LMP 阻塞分量。文献［7］提出将线路损耗平均分配至其两端节点，统计每个节点累计网损量来计算网损分布因子的方法，并推导了网损因子可以用节点注入功率与直流灵敏度计算，基于此提出了直流迭代的LMP 计算方法，通过多次迭代可得到更准确的网损。文献［9］研究了交直流迭代的网损估计方法，计算交流潮流后将支路损耗平均分配至两端节点来计算网损分布因子。文献［10］提出了基于支路线损因子的LMP 方法，将网损从系统级细分至支路级，可以更精确地表示线路潮流。

利用网损因子估算网损的方法的计算精度会受参考断面的影响，文献［7，21］分别证明了利用边际网损因子计算的网损为系统真实网损的2 倍。事实上，网损为节点注入功率的二次函数［22］，因此将网损建模成分段线性函数的方法也被用于LMP 计算［23］，但是会存在当LMP 为负时需要引入整形变量才能保证计算精度的问题［6，14］。

另外一种LMP 计算方法则是利用线性化的直流潮流方程建模，节点功率平衡方程的对偶乘子即为LMP［24-25］，这种建模方法还可以考虑无功功率和电压的影响，能进一步提高LMP 的准确性［6，8］。缺点是需要借助其他方法将LMP 分解为3 个分量，文献［24-25］提出了一种不受平衡机影响的LMP 分解方法，但该方法仅能保证不同节点阻塞分量的差值不受平衡机影响，每个节点的阻塞分量仍然受平衡机影响。

任何直流的近似方法都会带来一定误差，在可接受的偏差范围内，目前被广泛理解和接受的LMP分解方法仍然是文献［12］提出的网损分布因子方法，在美国PJM、MISO、ISO-NE 等多个电力市场中得到应用。文献［4，26］通过将该方法的结果与交流潮流对比，验证了基于网损分布因子的LMP 方法的有效性与实用性。该方法建模简单，且LMP 的阻塞分量不依赖参考节点的选择，其计算模型M-Ⅰ可用式（2）描述。

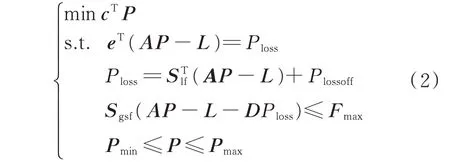
式中:c 为发电机报价曲线；e 为所有元素均为1 的列向量；P 为发电机出力向量；L 为母线负荷预测向量；Plossoff为系统网损预置偏差量，采用参考断面计算获得；A 为发电机与节点的关联矩阵，其元素Ai，g=1 表 示 发 电 机g 与 节 点i 关 联；Slf为 节 点 的 网损因子向量；Sgsf为支路与节点的直流灵敏度矩阵；Pmax和Pmin分别为机组有功出力的上、下限；Fmax为线路有功功率上限；D 为网损分布因子，满足eTD=1。

利用模型M-Ⅰ计算的LMP 及各分量分别为:

式中:λ，λe，λl，λc分别为LMP、LMP 能量分量、LMP网损分量和LMP 阻塞分量；τ 为式（2）中第3 行约束的影子价格；μ 为式（2）中第4 行潮流约束的影子价格。

模型M-Ⅰ有以下几个优点使其在考虑LMP 的现货市场中得到广泛应用:平衡节点的选择不影响LMP（λ），不影响LMP 阻塞分量λc，也不影响能量价格与网损分量之和λe+λl。

2 发用电负荷偏差问题分析

2.1 不考虑网损时发用电负荷偏差问题分析

如前文所述，中国的发电调度机构是以系统负荷为依据来编制发电计划，系统负荷是指发电机机端出力总和，当不考虑网损时，系统负荷等于母线负荷总和与负荷偏差之和，功率平衡方程为:

式中:Psysload为系统负荷；Poffset为负荷偏差。

负荷偏差相当于在系统中存在一个虚拟负荷，其大小和正负则会决定发电侧总的出清量。如果负荷偏差为正，则出清总量增大，会抬高系统LMP；反之出清总量减小，会降低系统LMP。对于负荷偏差，通常的做法是将其分配至所有负荷［5］，这将会影响系统的潮流。事实上，即使负荷偏差不分配给负荷节点亦如此，此时相当于将负荷偏差全部分配给机组，机组出力被分成了2 个部分，一部分通过电网供给节点的真实负荷，另外一部分供给的虚拟负荷。因此，负荷偏差必然分配至系统的某些节点，用分配因子w1，w2，…，wn表示其在各节点之间的分配比例，则只要满足∑wj=1，所有节点分摊的负荷偏差之和就等于总的负荷偏差。

不考虑系统网损时，负荷偏差可以直接用系统负荷减母线负荷的总和得到，然后利用负荷偏差分配因子修正各节点负荷即可求解，此时发电计划总和等于系统负荷。下面通过简单的三节点算例分析不考虑网损时，负荷偏差及分配因子对LMP 的影响。三节点算例线路参数、机组容量与报价见图1。图中，母线负荷L3=150 MW 位于节点3；系统负荷为160 MW；负荷偏差为10 MW；Pmax，1，Pmax，2，Pmax，3分别为机组G1，G2，G3的最大出力；C1，C2，C3分别为机组G1，G2，G3的申报电能量价格；x1，x2，x3分别为线路1，2，3 的电抗。

图1 三节点模型示意图Fig.1 Schematic diagram of 3-node model

多个场景下机组出力、线路潮流和LMP 情况如附录A 表A1 所示。其中，算例3-1 与算例3-2 不考虑网络约束，算例3-3 与算例3-4 考虑线路2 的潮流限额为95 MW，算例3-1 与算例3-3 将负荷偏差分配至节点1，算例3-2 与算例3-4 将负荷偏差分配至节点2。无网络阻塞时，负荷偏差分配至不同的节点不会影响机组中标出力和LMP，但影响线路潮流；有网络阻塞时，负荷偏差分配至不同的节点不仅会影响机组中标出力，还会影响线路潮流和LMP。

2.2 考虑网损的发用电负荷偏差分析

当考虑系统网损时，系统负荷等于母线负荷、系统网损、负荷偏差之和，功率平衡方程为:

不难理解，当且仅当式（8）中负荷偏差等于0时，利用母线负荷计算的发电计划总和才等于系统负荷。由于系统网损是节点注入功率的函数，节点注入功率又等于节点发电与负荷之差，则在机组出力确定之前系统网损必然是未知量，因此，负荷偏差亦未知且数值必然不为0。

新一轮电力市场改革中首批8 家试点单位的市场规则均明确规定现货市场采用系统负荷进行出清或可靠性机组组合计算，使用母线负荷计算潮流。部分试点单位对系统负荷与母线负荷的偏差处理方法做了明确规定。浙江现货规则规定:将系统负荷按照每个时段的负荷分配因子分配到调度网络节点，生成母线负荷。山东、山西现货规则规定:当母线负荷预测之和与全网系统负荷预测存在偏差时，以各节点的负荷预测值为基础按比例分摊偏差。但是，规则并未进一步明确在负荷偏差的分摊过程中如何处理系统网损。

正如2.1 节分析，不考虑网损时，将系统负荷与母线负荷偏差按照一定比例分配至负荷节点的方法是可行的。但是，忽略不同节点对系统网损的影响则可能带来很大的LMP 误差，一项针对美国纽约地区的研究结果表明，由网损造成不同地区LMP 的差异可达到20%［27］。然而，如果在出清模型中考虑系统网损，则出清总量等于系统负荷与网损之和，导致出清总量增加，抬高总购电成本。

本文将针对上述情况，在文献［12］所提模型M-Ⅰ的基础上，提出可精确计算系统网损和负荷偏差的LMP 模型。

3 考虑系统网损与负荷偏差的LMP 模型

系统网损与负荷偏差性质不同，系统网损来源于支路损耗，可用网损分布因子将其分摊至全网所有节点，该方法被证明是有效的［4，26］。而负荷偏差则是系统负荷与母线负荷预测的偏差，由于系统负荷是计划制定的依据，则可认为负荷偏差是母线负荷预测导致的，正如试点单位规则所述，将其分配至母线负荷是普遍采用的方法。考虑系统网损与负荷偏差模型的难点在于二者是互相耦合影响的，本文采用网损分布因子将系统网损分摊至所有节点，负荷偏差分配因子将负荷偏差分摊至负荷节点相结合的思路，提出基于迭代的LMP 模型、两步法LMP 模型2 种方法。

3.1 基于迭代的LMP 模型

迭代法的思路是将系统网损与负荷偏差解耦:固定负荷偏差计算系统网损，通过迭代不断修正负荷偏差，实现系统网损的精确计算。模型M-Ⅰ实现了基于母线负荷的网损计算，但由于负荷偏差的存在，所得发电总和并不等于系统负荷。基于模型M-Ⅰ改进的迭代法模型M-Ⅱ详见式（9），系统平衡约束、网损表达式、支路潮流表达式与模型M-Ⅰ基本一致；不同之处在于模型中负荷不再是初始负荷，而是计及了第1 至第k-1 次计算的累计负荷偏差修正后的值。

式中:L(k)为第k 迭代求解使用的母线负荷；P(k)loss为第k 次迭代求解时的系统网损。

假设第k 次迭代时，模型M-Ⅱ求解的发电计划总和为P(k)gen，则计算k 次迭代后的负荷偏差P(k)offset如式（10）所示，修正节点负荷如式（11）所示。然后，用新的负荷替换模型M-Ⅱ中的值，进入第k+1 次迭代，重新求解。

式中:W 为负荷偏差分配因子，满足eTW =1。

迭代法计算流程如图2 所示，在第1 次迭代时可简化处理，设置负荷偏差为0，用原始母线负荷进行计算。在每次求解后利用式（10）计算负荷偏差，并检查是否满足收敛条件，若收敛则用式（9）中第3 行网损约束的影子价格τ、式（9）中第4 行潮流约束的影子价格μ，采用式（3）—式（6）的分解方法计算LMP。若不满足收敛条件，则利用式（11）修正母线负荷，重新求解模型M-Ⅱ，直至算法收敛。

图2 基于迭代的LMP 算法的计算流程图Fig.2 Flow chart of calculation for iteration-based LMP algorithm

基于迭代的LMP 算法通常需要通过多次计算才能达到收敛精度，在工程应用中会存在计算效率低的问题，两步法LMP 模型可以解决计算效率低的问题。

3.2 两步法LMP 模型

两步法的思路如下:第1 步以系统负荷建立平衡约束构建模型并计算系统网损、负荷偏差；第2 步以母线负荷、第1 步中计算的负荷偏差为约束，构建模型计算LMP。第1 步的模型M-Ⅲ如式（12）所示。其中，式（12）中第2 行约束式为发电侧系统平衡约束，其含义为发电计划总和等于系统负荷；式（12）中第3 行约束式为负荷侧系统平衡约束，其含义为系统负荷等于母线负荷总和、系统网损、负荷偏差之和；式（12）中第4 行约束式为系统网损约束，采用网损因子计算网损，并在网损计算时考虑了负荷偏差分摊对系统网损的影响；式（12）中第5 行约束式为支路潮流约束，不等号左侧支路潮流表达式考虑了系统网损、负荷偏差分摊量对支路潮流的影响，利用网损分布因子D 将系统网损分摊至所有节点，负荷偏差分配因子W 将负荷偏差分配至负荷节点。

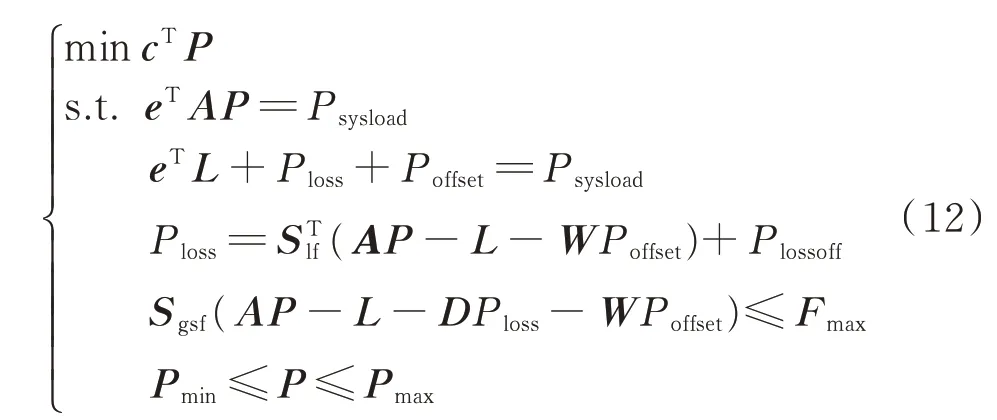
第2 步，将模型M-Ⅲ中求解的负荷偏差固定，运行模型M-Ⅳ，得到式（13）中第3 行网损约束式的影子价格τ、式（13）中第4 行潮流约束的影子价格μ，然后利用式（3）—式（6）计算LMP。两步法的LMP计算流程如图3 所示。

式中:Poffset为常量，是第1 步模型M-Ⅲ计算后的值。

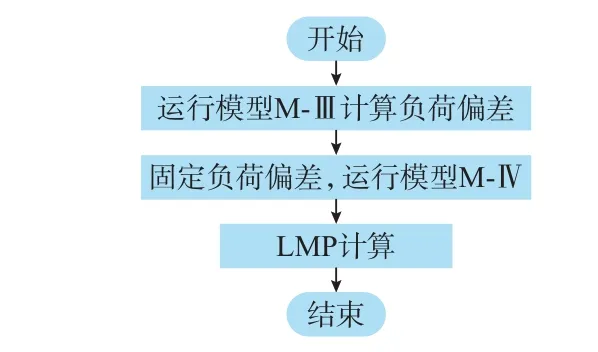
图3 两步法LMP 算法的计算流程图Fig.3 Flow chart of calculation for two-stage LMP algorithm

模型M-Ⅱ和M-Ⅳ中对系统网损的建模仍然采用了网损分布因子的方式，因此模型完全可以继承模型M-Ⅰ的优点，即采用模型M-Ⅱ或M-Ⅳ计算的LMP 阻塞分量与参考节点选择无关。模型也可以适用于不考虑网损的情况，只需要在计算时设置网损分布因子D 为0 即可，此时负荷偏差将会全部按照负荷偏差分配因子W 分摊至所有节点。

模型M-Ⅱ，M-Ⅲ，M-Ⅳ为线性模型，采用线性规划法即可求解。上述模型仅考虑单时段，但可以很容易扩展至多个时段，也可以增加机组爬坡等约束以满足模型使用化需求。另外，该方法也适用于以系统负荷为依据，编制发电计划的所有优化模型，包括安全约束机组组合模型。集中式电力市场的出清流程通常是先求解机组组合模型，然后固定机组启停状态求解经济调度模型来计算机组出力与电价［9］。由于迭代的方法需要通过多次计算才能收敛，使用模型M-Ⅱ建立机组组合模型求解时，会降低市场出清效率。此时可在出清环节按照模型M-Ⅲ建立机组组合模型计算系统网损与负荷偏差，然后按照模型M-Ⅳ建立经济调度模型，计算机组出力与电价。

4 算例分析

基于IEEE 14 节点模型构造算例，对本文研究内容进行验证。算例中机组采用分段报价，数据详见附录A 表A2，母线负荷预测详见表A3，预测总和为455 MW；支路1-2 传输限额为150 MW；网损分布因子基于参考断面（参考断面取自MATPOWER数据），统计支路损耗均分至支路两端节点计算得到［9］，数据详见表A4。

4.1 模型M-Ⅱ和M-Ⅳ的有效性验证

本节对模型M-Ⅱ和M-Ⅳ的计算效果进行验证，计算场景为:假设系统负荷预测为500 MW，负荷偏差分配因子采用归一化的节点负荷比例；网损因子基于参考断面选用节点1 为参考节点计算得到，数据详见附录A 表A4。利用网损分布因子分摊系统网损与负荷偏差分配因子分配负荷偏差。模型M-Ⅱ中的负荷偏差收敛精度设定为10-4，迭代计算过程详见表A5，算法经4 次迭代后收敛，负荷偏差满足收敛精度要求。

附录A 表A6 对比了模型M-Ⅱ和M-Ⅳ的优化目标与总发电，从表中可知，二者存在微小差异，这是模型M-Ⅱ收敛精度导致的，不影响工程应用。

附录A 表A7 对比了模型M-Ⅱ和M-Ⅳ的母线负荷与LMP 结果，二者计算结果完全相同。模型M-Ⅱ第1 次迭代的结果即是模型M-Ⅰ的计算结果，由表A7 可知，存在25 MW 的负荷偏差。由于负荷偏差导致边际机组发生变化（边际机组G3第2 段中标），LMP 也存在一定偏差。

附录A 表A8 和表A9 进一步对比了不同网损因子时的LMP 各分量，表A8 为使用节点1 为参考节点计算的网损因子求解的结果，表A9 为采用分布式参考节点计算的网损因子求解的结果，网损因子数据详见表A4。结果表明，采用不同网损因子计算的LMP 阻塞分量相同、能量分量与网损分量之和也相同，因此，本文方法仍然可以保持文献［12］所述模型M-Ⅰ的优点。

4.2 考虑网损的负荷偏差分摊模型的必要性

将本文方法与传统的不考虑网损的直流模型进行对比，在不考虑网损的直流模型中，系统网损与负荷偏差将全部按照负荷偏差分配因子分摊至所有负荷。附录A 表A10 展示了不考虑网损的直流模型的LMP 结果，仅包括能量分量、阻塞分量，无网损分量。

本文方法与不考虑网损的直流方法的LMP 对比如图4 所示，边际机组所在节点的LMP 相同（节点1 和节点3 的LMP 相同），其余节点的LMP 不同。这是因为当边际机组所在节点负荷增加时，只需边际机组增加出力即可满足负荷增加的需求，2 种模型均不会导致网损变化。非边际机组节点负荷增加时，考虑网损的模型的边际机组的增量与负荷增量不再相同，故LMP 亦不同。这说明，当采用直接将系统网损按照负荷偏差分配因子分摊至节点的方式时，LMP 不能准确反映不同节点对网损的影响，负荷偏差分摊时必须考虑网损才能得到准确的价格信号。

图4 2 种网损分摊方法的LMP 对比Fig.4 Comparison of LMP between two loss allocation methods

4.3 负荷偏差分配因子对LMP 的影响

2.1 节已经分析了不考虑网损时，不同的负荷偏差分配因子可能会对LMP 造成影响，本节通过3 个算例分析考虑网损时，不同负荷偏差分配因子对LMP 的影响。3 个案例分别为:算例14-1 采用各节点负荷比例作为负荷偏差分配因子；算例14-2 中节点2，3，9 的 负 荷 偏 差 分 配 因 子 分 别 为0.25，0.5，0.25，其余节点的为0；算例14-3 中节点1 和9 的负荷偏差分配因子分别为0.8 和0.2，其余节点的为0。

图5 对比了3 个算例的LMP，附录A 表A11 展示了3 个算例的机组出力。算例14-1 和算例14-2 的LMP 完全相同，这是因为虽然负荷偏差分配因子不同，但边际机组相同，故LMP 亦完全相同。算例14-3 的LMP 偏低，是因为算例14-3 将很大的负荷偏差分配给报价较低且由于网络阻塞无法送出电力的节点1，导致机组G1出力增加，而报价更贵的机组G3中标出力减少，系统的边际成本更便宜。

以上分析可知，不同的负荷偏差分配因子方案，只要边际机组相同，则LMP 相同。

4.4 负荷偏差水平对LMP 的影响

图5 不同负荷偏差分配因子下LMP 对比Fig.5 Comparison of LMP with different load deviation distribution factors

针对不同负荷偏差水平对LMP 的影响，设计多个场景进行分析，每个场景除负荷偏差分配因子外，其余条件完全相同。计算时假定母线负荷预测不变，系统负荷连续变化，模拟不同负荷偏差水平。系统负荷变化范围为450～500 MW（偏差百分比为-5%～5%），负荷连续变化步长为0.2 MW。场景1，2，3 的负荷偏差分配因子分别与4.3 节算例14-1、算例14-2、算例14-3 的相同。

图6 展示了不同场景、不同负荷偏差下节点2的LMP 的变化趋势，当负荷连续变化时LMP 出现跳变，LMP 跳变时负荷偏差不同。原因是不同的负荷水平、不同的负荷偏差分配因子使边际机组不同。例如，在场景1 中，当系统负荷从462.2 MW 增加至462.4 MW 时，机组G3的出力从49.89 MW 变为50.07 MW，边际机组发生变化；而在场景2 中，当系统负荷从463.4 MW 增加至463.6 MW 时，机组G3的出力则从49.94 MW 变为50.14 MW，边际机组才发生变化。由图中还可知，系统负荷在463.6～488.2 MW 范围内连续变化时（对应的负荷预测偏差为-2.6%～2.5%），不同的负荷偏差分配因子下的节点2 的LMP 完全相同。

图6 不同负荷偏差下节点2 的LMP 对比Fig.6 LMP Comparison of node 2 with different load deviations

本文定义LMP 综合偏差表征所有场景的LMP偏离平均值的程度，节点i 的LMP 综合偏差εi和平均LMP 的综合偏差εˉ的计算方法详见式（14）—式（18）。

式中:S 为场景数；N 为节点数；λavgi为不同场景节点i的LMP 算术平均值；λs，i为场景s 中节点i 的LMPs为场景s 的平均LMP；-λavg为所有场景平均LMP 的算术平均值。

附 录A 图A1 展 示 了 节 点2，3 的LMP 和 平 均LMP 的综合偏差，当系统负荷在463.6～488.2 MW范围内时，综合偏差均为0，即不同场景的LMP 完全相同。

利用IEEE 118 节点模型进一步分析不同负荷偏差和偏差分配因子对LMP 的影响（数据来源于MATPOWER 软件，以其公开的case118 断面计算网损因子和网损分布因子，机组成本采用二次成本曲线分段线性处理得到（本算例分5 段）。以节点负荷作为母线负荷预测，并假定系统负荷变化范围为4 100～4 540 MW 来模拟不同负荷偏差水平（偏差百分比约为-5%～5%），负荷连续变化步长设为1 MW。同样构造3 个场景，每个场景设定不同的负荷偏差分配因子:场景1 采用节点负荷比例作为负荷偏差分配因子，场景2 采用网损分布因子作为负荷偏差因子，场景3 采用节点平均分配的方式。附录A 图A2 展示了当负荷连续变化时，节点50、节点100 的LMP 和平均LMP 的综合偏差，当负荷偏差较小时（-2.05%～2.5%），综合偏差为0，即不同负荷偏差分配因子的LMP 完全相同。

IEEE 14 节点和IEEE 118 节点模型仿真结果均表明，当负荷偏差水平较低时，不同的负荷偏差分配因子不会影响LMP。因此，提高负荷预测的准确性，可以一定程度上改善模型对负荷偏差分配因子方案的依赖，提高本文模型的工程实用效果。

5 结语

本文针对中国调度机构以系统负荷为依据出清和计算LMP 时，由于存在负荷偏差无法精确计算系统网损的问题，提出了2 种计算模型。模型中考虑了系统网损与负荷偏差的相互耦合影响，可以精确计算系统网损与负荷偏差。与直接将网损和偏差分摊至节点的模型相比，采用本文所提模型计算的LMP 可以正确反映不同节点对系统网损的影响。算例分析表明，不同的负荷偏差分配因子对LMP 有一定影响，但通过提高负荷预测准确性，可以降低LMP 对负荷偏差分配因子的依赖。本文的不足之处在于，网损因子与网损分布因子是基于参考断面计算得到的，在后续的求解过程中并未更新，使得网损存在一定的误差，在模型中考虑更精确的网损因子和网损分布因子是下一步的研究方向。

中国新一轮电力市场改革尚处起步阶段，多数试点单位均采用单边报价以系统负荷出清的方式起步，本文所提方法可用于市场初期的出清与LMP 计算。在双边竞争的电力市场中，在市场出清后会执行基于预测负荷的可靠性机组组合以保证供电可靠性，故本文所提方法也可用于双边竞争市场下的可靠性机组组合出清环节。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。