考虑动态备用需求曲线的电能量-备用耦合出清模型

刘润泽，荆朝霞，刘 煜

（华南理工大学电力学院，广东省广州市510640）

0 引言

自《关于进一步深化电力体制改革的若干意见》［1］发布以来，中国电力市场改革取得显著成效，然而也存在缺失收入（missing money）问题［2］，部分电厂无法收回全部成本。改革前由“准许成本+合理收益”确定上网电价，不存在此问题。但在电力市场环境下，由于价格帽、需求弹性不足、可再生补贴等原因［3］，缺失收入问题普遍存在，引发发电投资激励不足、需求响应激励不足等其他问题［4］，造成发电容量充裕度不足。电力市场中保证发电容量充裕度的关键在于解决缺失收入问题。

世界电力市场的实践表明，解决缺失收入问题主要有2 种思路:容量补偿［5-6］和稀缺电价［7-8］。容量补偿和稀缺电价皆为广义概念，容量补偿包括面向全部发电容量的容量市场［9］和面向部分发电容量的策略备用［10-11］等机制；稀缺电价包括高报价上限、稀缺惩罚因子和价格增量等机制［12］。容量补偿的典型机制是由市场运营机构预测未来容量需求并进行拍卖，存在预测精确性难以保证、容量支付导致能量价格降低等问题［13］。

稀缺电价机制下无须预估容量需求，能量价格可以较好地反映实时供需，但若采用市场主体直接申报高价的机制，将导致价格波动不可控、发电市场力控制困难等问题。稀缺惩罚因子机制和价格增量机制本质上都是由市场运营机构设定一个具有弹性的备用需求曲线（operation reserve demand curve，ORDC），二者区别在于稀缺惩罚因子机制采用阶梯状ORDC［14］，价格增量机制采用连续型ORDC［8，15］。在基于ORDC 的机制下，发电市场主体的报价基于成本，既可以解决缺失收入的问题，又可以避免价格不可控的风险，且连续型ORDC 比阶梯状ORDC 更为精确。

价格增量机制下的关键问题是不同情况下价格增量的计算，而价格增量计算的核心是ORDC。ORDC 反映用户的用电价值（失电损失），其是否反映真实供需是影响价格增量机制有效性的一个关键因素。实际电力系统中电力供需时刻变化，因此ORDC 也应动态变化。但在实践中，往往采取静态ORDC。例如美国得克萨斯州每季度公布1 次ORDC 参数，季度内的ORDC 不变［16-17］。

ORDC 曲线的制定与应用方面已有较多研究。在静态ORDC 方面，文献［8，18］提出基于ORDC 的价格增量计算基础模型。在动态ORDC 方面，文献［19］基于负荷、可再生预测来动态修改运行备用需求量，但ORDC 为阶梯状，分段内备用价值相同，不能完全反映备用容量和备用价值间的动态变化关系。文献［20］考虑风险偏好计算ORDC，但是未根据响应时间对备用产品的价值进行区分。文献［21］将动态ORDC 应用于电能量与备用联合优化出清模型，但未考虑网络约束。

目前研究主要存在如下问题:①关于动态ORDC 的考虑因素不够完整，例如未考虑可再生能源波动性［8］、未考虑备用品种的多样性［20-21］；②关于ORDC 的形状，很多文献采用类似于纽约独立系统运营商（independent system operator of New York，NYISO）等市场的阶梯形ORDC［19，22-25］，较为简单，但准确性不如连续的ORDC；③现有研究缺乏对实际市场的模拟，忽略线路、机组等的约束［20-21］及省略机组的备用报价［21］，且未能从ORDC 推导、出清、价格机制等方面进行全面分析。

本文在上述研究基础上，首先制定考虑风电、负荷不确定性和不同备用产品的连续型ORDC；然后建立电能量-备用联合的现货出清模型及其扩展模型；由此推导备用需求曲线模式下的备用价格增量一般性计算公式。分析与国外现有机制的区别，为中国稀缺定价机制设计提供借鉴。最终，通过算例对上述模型进行验证。

1 稀缺定价机制及ORDC 制定

电力系统中定义的备用产品不同，对应的ORDC 也不同。本文计算备用价格增量的步骤如下。

步骤1:根据ORDC 的物理意义，由调度修正模型推导不同备用品种的ORDC，并计算备用的社会福利。

步骤2:建立现货市场出清模型及其考虑备用社会福利的扩展模型，根据含有电能量和备用2 类产品的社会福利最大化函数，推导出含备用价格增量的节点电价表示公式。

步骤3:由步骤2 的价格机制，根据步骤1 算出备用的社会福利，计算备用价格增量的具体值，进一步得出含稀缺价值的节点价格。

1.1 备用需求曲线的定义

ORDC 的构建基于2 个量:失负荷价值（value of lost load，VOLL）和 失 负 荷 概 率（loss of load probability，LOLP）。由于电力市场中需求侧弹性不足，备用价值很难通过出清结果直接反映，因此ORDC 往往由监管机构定义。ORDC 示意图如图1所示，其中ORDC 计算公式为:

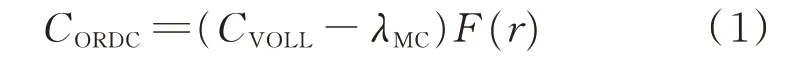
式中:CORDC为备用容量成本；CVOLL为VOLL；λMC为系统边际成本；F(r)表示系统实际备用容量r 低于最小应急备用水平的概率；r 为实际备用容量。

CVOLL代表监管机构对发电紧缺期间非自愿负荷削减造成的成本，其3 种主要计算方法为:客户调查 法［26］、宏 观 经 济 分 析 法［27］、实 际 停 电 事 件 分 析法［28］。但是，目前并没有通用的计算方法。美国独立系统运营商（independent system operator，ISO）/区域输电组织（regional transmission organization，RTO）普遍未公开CVOLL的计算方法；得克萨斯州电力市场采用的CVOLL是9 000 美元/（MW·h），而且多年保持不变。本文将CVOLL看作定值。

图1 ORDC 示意图Fig. 1 Schematic diagram of ORDC

F（r）基于LOLP 定义，代表系统中的备用水平小于或等于最小应急备用要求的概率。在曲线的水平段，系统可用备用水平不大于系统可靠性要求的备用最低要求，必定会削减负荷，备用价格达到设定的VOLL；在曲线的倾斜段，当备用容量大于最小紧急备用需求时，需求曲线服从LOLP 分布。对于一个给定的备用水平r，F（r）计算公式为:

式中:X 为系统最小应急备用要求，一般由调度机构设 定；FLOLP(σ，μ，r-X )为LOLP；FCDF(σ，μ，r)为备用水平r 下均值为μ、标准差为σ 的正态分布函数的累积分布函数，详见附录A 图A1。

1.2 不同备用类型的ORDC 推导

按照响应时间，将备用分为2 类:实时在线备用容量rⅠ（10 min 响应）和实时离线备用容量rⅡ（30 min 响应）。其中，rⅠ包括参与市场出清的发电资源、调频、负荷需求响应，以及10 min 响应的资源容量。rⅡ则是指30 min 响应的备用容量。1 h 内的负荷预测误差和可再生能源出力波动等不确定量（净负荷变化）如图2 所示。鉴于不同类型备用资源的响应时间差异，其可处理的净负荷变化时间间隔也不同。由于rⅠ响应能力高于rⅡ，可替代rⅡ处理30～60 min 的变化量。因此，区间Ⅰ的变化量仅可由rⅠ满足，区间Ⅱ的变化量可由rⅠ与rⅡ共同满足。

ORDC 基于备用产品的调用模型构建，即系统发生扰动时备用资源调用产生的社会福利。备用资源调用以社会总福利最大化为目标，备用产生的社会福利为系统减少的损失与调用备用容量所需的能量成本之差，可通过以下公式得到:

式中:ΔLΣ，w为系统因事件w 产生的净功率波动值；Pi为机组i 的调度量；ΔPi，w为机组i 因为事件w 产生的调度变化量，为决策变量；ΔPΣ，w为系统调度变化量，是ΔPi，w之 和；G 为 系 统 中 所 有 机 组 的 集 合；Ci(x)为机组i 在出力为x 的情况下的发电成本；θw和πw分别为对应约束的拉格朗日乘子。

式（5）表示调度变化量不超过系统净功率波动值，满足功率平衡约束；式（6）表示调度变化量不应超过备用容量，满足备用容量约束。拉格朗日乘子πw是对系统内部备用资源的一种客观估计，其大小客观反映备用资源在系统内的稀缺程度，经济含义为增加单位备用容量引起的社会福利增加量。

以上优化问题的库恩-塔克（Karush-Kuhn-Tucker，KKT）条件如下所示。

1）原始可行性

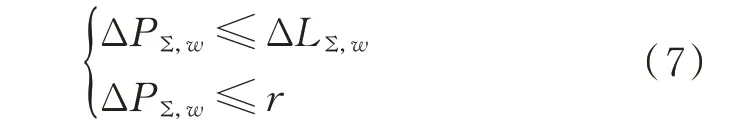
2）对偶可行性

3）定常方程式

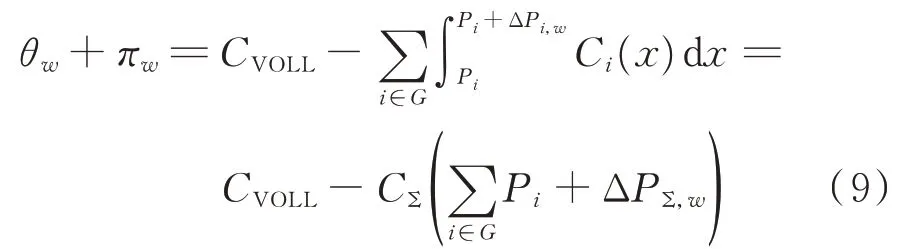
式中:CΣ为系统总发电成本，是系统中所有机组发电成本Ci的总和。

4）互补松驰性

式中:ρw为事件w 发生的概率；Ω 为事件集合。

下面推导区间Ⅰ的均值和方差。本文利用如图2 所示的阶跃函数来近似计算净负荷的变化。假设区间Ⅰ的时长占整个时长的比为δ，由于本文rⅠ中10 min响应使得系统30 min恢复正常，rⅡ中30 min响应使得系统60 min 恢复正常，因此文中δ=0.5。1 h 内的总功率净扰动ΔLΣ，w为2 个矩形面 积 之 和，即ΔLΣ，w=δΔLⅠ，Σ，w+(1-δ)ΔLⅡ，Σ，w，服从均值为μ、方差为τ 的N(μ，τ)正态分布；其中ΔLⅠ，Σ，w、ΔLⅡ，Σ，w分别为区间Ⅰ、区间Ⅱ的功率净扰动。进一步假设区间Ⅰ、区间Ⅱ的功率净扰动是2 个独立的事件，服从相同的正态分布。区间内的功 率 净 扰 动 的 均 值Ew(ΔLΣ，w)和 方 差Var，w(ΔLΣ，w)满足以下公式:

因此，区间Ⅰ内功率净扰动的均值μⅠ和标准差τⅠ分别为:

因此，2 类区间下的LOLP 分别为:

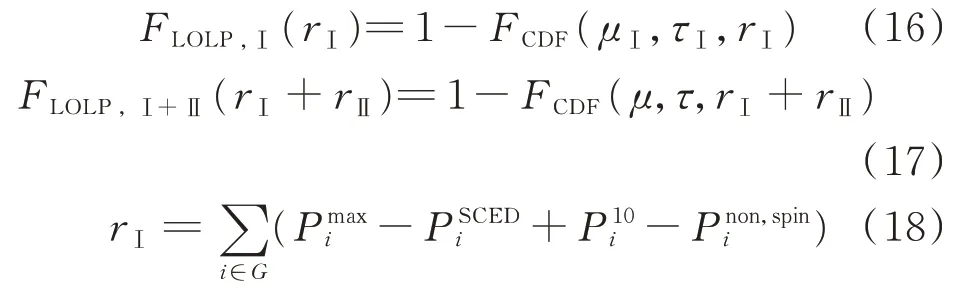
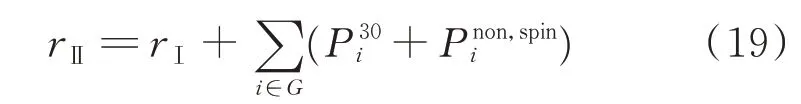
式中:Pmaxi为机组i 的最大发电功率；PSCEDi为机组i调度功率；P10i和P30i分别为机组i 的10 min 和30 min备用容量；Pnon，spini为机组i 的非旋转备用容量。

1.3 基于多种不确定性因素的动态ORDC

在1 年中的不同月份、1 d 中不同的时间，LOLP曲线的均值、标准差的数值不同。得克萨斯州电力市场中，每个季节使用1 组提前发布的LOLP 静态参数，难以反映系统真实不确定性。本文构造动态ORDC，其LOLP 可以根据运行情况不同而动态变化。制定ORDC 的LOLP 时，需考虑可再生能源的不确定性以及负荷的预测误差等多种不确定性因素。主要考虑的不确定因素如下。

1）风电预测不确定性。假设风电功率预测误差为正态分布［29］，均值为0，标准差由实际数据计算得出。时刻t 风电功率预测值PW，t为:

2）负荷预测不确定性。负荷的不确定性主要来源于预测误差，一般假设负荷的不确定性为正态分布［30］，均值为0，标准差由实际数据计算得出。同理，时刻t 负荷预测值Lt为:

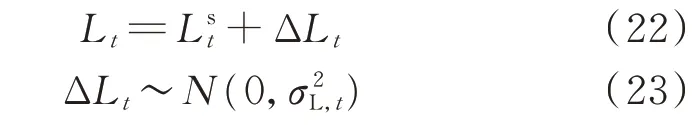
假设以上2 类不确定性来源相互独立。参照图2，在区间Ⅰ开始时已经发生事件，定义整个区间内的总不确定性为净功率波动ΔPt=ΔPW，t-ΔLt，由于ΔPW，t和ΔLt均服从正态分布，因此总不确定性也服从正态分布。给定风电功率预测误差ΔPW，t、负荷预 测 误 差 ΔLt的 概 率 密 度 函 数fΔPW，t(ΔPW，t)、fΔLt(ΔLt)，可通过卷积计算净功率波动的概率分布:

式中:PW，T为风电总装机容量；u 为积分变量。

2 现货出清模型

2.1 目标函数

实时备用市场与电能量市场联合出清，最小化全时段所有机组的运行成本与备用辅助服务成本。

2.2 系统功率平衡约束

式 中:Lj，t为 系 统 在 时 刻t 的 负 荷；GR为 常 规 机 组 集合；D 为系统中所有负荷集合；λ 为对应约束的拉格朗日乘子。

2.3 发电机组运行特性约束

2.3.1 功率上、下限约束

式中:Pmini为 机 组i 的 最 小 发 电 功 率；yi，t为 机 组i 的状态，为0-1 变量，0 表示离线停机状态，1 表示在线运行状态。

2.3.2 爬坡约束

2.4 网络约束

线路（断面）的潮流约束为:

式中:Pl，t，Ln为 线路（断面）l 的潮流 功率；P为 线路（断面）l 潮流功率约束；ξl为对应约束的拉格朗日乘子。

2.5 备用约束

参考中国浙江电力现货市场规则，将备用分为10 min响应和30 min 响应。

1）10 min 备用约束

2）30 min 备用约束

3 考虑备用需求曲线的价格机制

ORDC 代表系统中每个备用水平对应的价值，可以反映备用价值的稀缺性，以价格增量的方式加到节点边际电价中。

3.1 不同备用类型的社会福利

在线备用容量的社会福利WⅠ为在线备用的ORDC 从0 到rⅠ的积分:

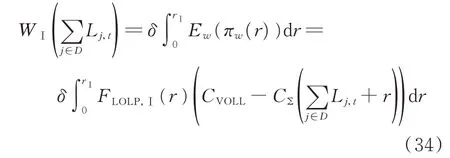
对应于区间Ⅱ的在线和离线备用社会福利WⅡ为:

3.2 不同备用类型的价格增量推导

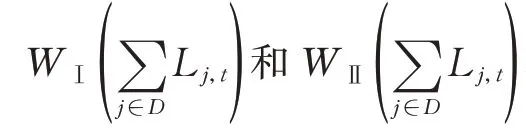
约束为第2 章中的式（26）—式（28）、式（31）。本节所述模型的拉格朗日对偶函数为:

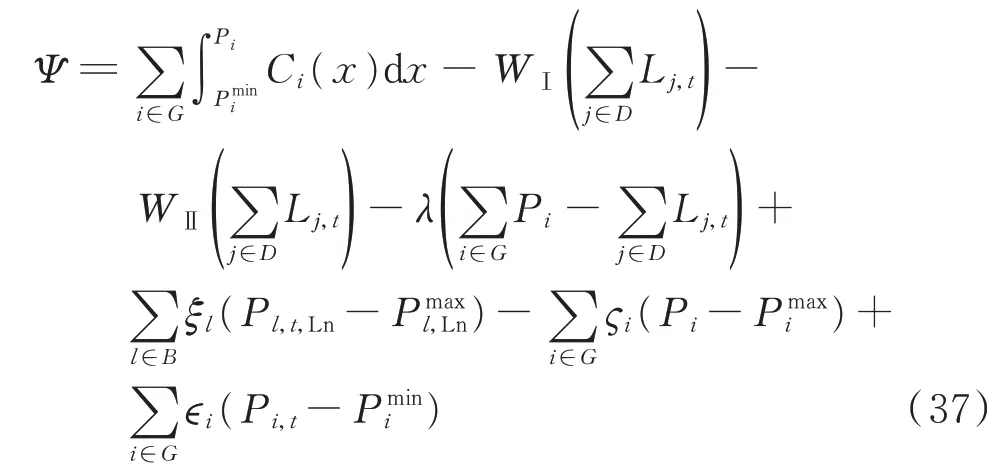
式中:B 为线路集合；ξl、ςi、ϵi为拉格朗日乘子。

每个节点j 的节点边际价格Jj为:

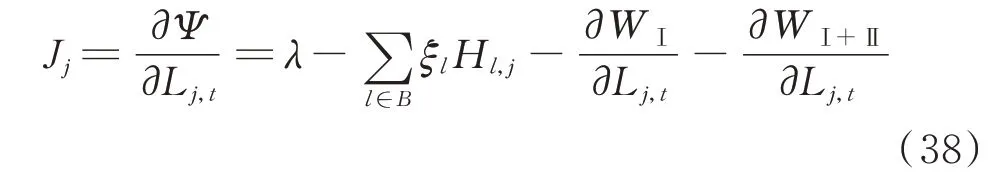
式 中:Hl，j为 节 点j 对 线 路l 的 发 电 转 移 因 子。

公式中子项可进一步化简为:

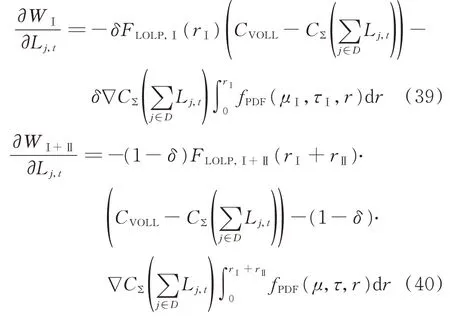
式中:fPDF为概率密度函数。

式（39）和式（40）分别考虑了不同备用品种的价格增量中的稀缺价格增量和价格提升增量。将式（39）和式（40）合并，可得价格提升增量Cadder和总的稀缺价格增量Sadder分别为:

可以看出，得克萨斯州的备用价格增量公式与本文推导结果的不同点在于，得克萨斯州忽略了备用价格增量的高阶项，即Cadder部分的值。将CΣ近似为系统电能量价格λ，忽略高阶项，即∇CΣ≈0，δ=0.5，可得备用价格增量γadder为:

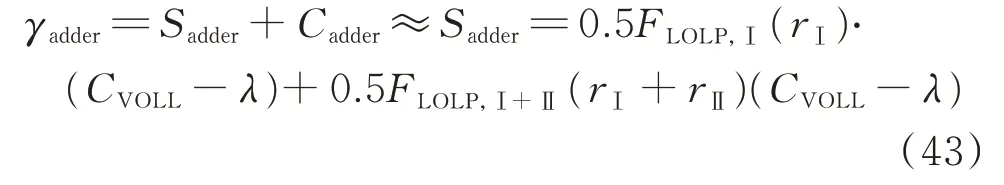
考虑到ORDC 带来的价格增量不会无限大，根据式（2），将式（43）进一步表示为:

式中:FⅠ和FⅠ+Ⅱ分别为区间Ⅰ和区间Ⅰ+Ⅱ的LOLP；γOR和γOFF分别为实时在线价格增量和实时离线价格增量。

计算FⅠ时，μⅠ=δμ=0.5μ，τⅠ={δ2τ2/[δ2+(1-δ)2]}1/2=0.707τ；计算FⅠ+Ⅱ时，直接使用δ 和μ 的值。因此，价格增量为:

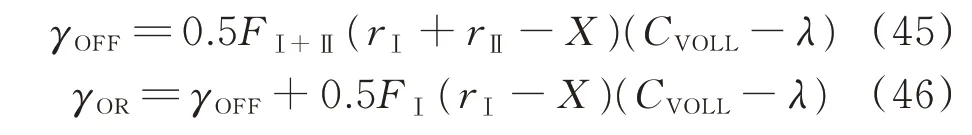
4 算例分析

为验证基于动态备用需求曲线的价格信号的有效性，本文以中国华东某省电网系统进行算例分析。1 d 内的系统总负荷曲线及不同风电状态下的出力曲线如附录A 图A2 所示。

4.1 不同可再生能源发电场景

选取3 个典型月份的数据，分别对应高、中、低3 种风电功率水平。计算不同可再生能源出力水平下的节点电价及备用价值，如图3 所示。其中λh、λm、λl分别表示可再生能源出力高、中、低3 种场景下的节点电价；γOR，h、γOR，m、γOR，l分别表示对应3 种场景的在线备用价格增量；γOFF，h、γOFF，m、γOFF，l分别表示对应3 种场景的离线备用价格增量。

备用价值通过γOR和γOFF价格增量反映。如1.2 节所述，10 min 响应资源可处理区间Ⅰ和Ⅱ内的净负荷波动，30 min 响应资源仅处理区间Ⅱ段内的净负荷波动，区间Ⅱ内的10 min 响应资源优先级大于30 min 响应资源，因此10 min 响应资源的备用价值应高于30 min 响应资源。图3 中，在不同可再生能源出力水平下，γOR价格增量曲线高于γOFF价格增量曲线，印证了10 min 响应资源在区间Ⅰ和Ⅱ内的备用价值高于30 min 响应资源在区间Ⅱ内的备用价值。

随着系统总负荷及可再生能源出力的变化，系统可响应资源的备用容量在不同时段也存在差异。在峰荷8—12 h 时段内，系统总负荷最大、同时风电出力最小，火电机组需增加出力以满足系统净负荷需求，导致对应该时段的可响应资源的备用容量也最小，备用稀缺。如图3 所示，在峰荷时段的价格增量γOR和γOFF会高于平时段、谷时段的价格增量，反映系统备用容量的稀缺程度。

在不同的可再生能源出力水平情况下，γOR和γOFF随可再生能源出力增大而递减。由于在同一系统总负荷水平下，风电功率上升造成火电机组出清电量减少，因此系统存在大量的火电机组可调用备用容量，此时备用资源不稀缺。如图3 所示，在3 种风电场景下，风电高出力时的价格增量最低，风电低功率时的价格增量最高。在同一负荷水平下，价格增量的大小均随着风电功率水平上升而减少。

图3 不同可再生能源出力水平下的节点边际电价及备用价格增量Fig.3 Locational marginal prices and reserve price adders at different power output levels of renewable energy

4.2 动态ORDC 曲线参数的影响

系统净负荷波动对价格增量的影响体现在ORDC 曲线的构造中，主要是通过系统净负荷波动误差服从正态分布的均值、标准差体现。为对比得克萨斯州静态ORDC 和本文动态ORDC，选取不同的负荷波动、风电功率波动的场景，比较2 种机制下，系统备用价格增量的结果。

如图4 所示，高、中、低3 种不同的负荷波动、可再生能源波动的不确定性场景下，case1 至case3 分别代表高、中、低3 种不确定性场景下基于动态ORDC 计算出来的备用价格增量及其组成；由于3 种场景下基于静态ORDC 计算出来的结果一致，因此统一用case4 代表基于静态ORDC 计算出来的备用价格增量及其组成部分。可以看出，若采用静态ORDC，在负荷或者可再生能源波动较大、系统发生突发时间或天气原因造成净负荷预测误差较大时，静态ORDC 不能反映这一波动，无法释放价格信号。

图4 动态ORDC 与静态ORDC 的备用价格增量对比Fig.4 Comparison of price adders of dynamic ORDC and static ORDC

4.3 备用价格增量高阶项的影响

备用价格增量的高阶项的计算公式由式（41）给出。如图5 所示，Sadder和Cadder分别表示价格增量高阶项和低阶项的数值。可以看出，高阶项的数值较之于低阶项的数值而言较小，且远小于节点边际电价的数值。在实际稀缺定价机制规则设计中，忽略此项对整体结果影响不大。

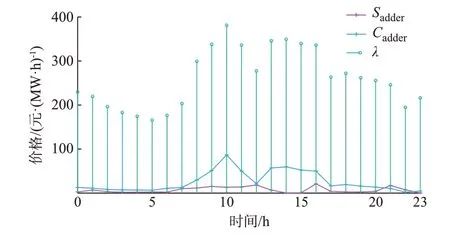
图5 备用价格增量高阶项Fig.5 Higher-order term of reserve price adders

5 结语

电力市场发展存在较强的路径依赖，市场运行后调整较为困难，因此发电容量充裕度机制初期方案的选择需要慎重。备用价格增量模式是充裕度机制的一种重要类型。本文在得克萨斯州连续型ORDC 的基础上，推导包含风电、负荷预测误差和不同备用类型的ORDC 动态确定方法，给出电能和备用联合优化的现货出清模型。通过算例分析，验证了备用价格增量可反映系统备用容量的稀缺程度，反映动态ORDC 机制的有效性。对不同类型备用对应的价格增量进行公式推导与算例比较，从数学的角度阐明不同备用资源的价值。本文主要结论与建议如下。

1）基于ORDC 的稀缺定价机制可以反映系统备用容量的稀缺程度。相对于容量市场难以准确计算需求、难以监管等问题，备用价格增量可以反映实时供需，通过每时每刻的价格信号指引发电投资。此外，由于容量市场的容量需求预测往往偏大，因此在中国电力市场中引入容量机制易造成消费者分摊过重负担，不利于电力市场改革成果和经济发展。而备用价格增量的数值一般较小，算例分析表明，备用价格增量约为节点边际电价的0%～15%，不会对市场价格产生巨大影响，适用于中国发电容量充裕度机制设计。

2）动态ORDC 和静态ORDC 的区别在于LOLP 不同，动态ORDC 比静态ORDC 更能反映系统真实波动状态。得克萨斯州提前发布静态ORDC 的方式虽然是一种简单可行的办法，但过于粗略。在中国电力市场建设中，若引入稀缺定价，可以采用本文提出的动态ORDC。ORDC 和出清模型可以分开计算，计算最终市场价格时，利用ORDC 计算每个时刻的稀缺性价格增量，将其加入本身的出清电价中，不会对现有出清系统的计算造成负担。

3）备用价格增量高阶项的数值与ORDC、系统中机组的成本曲线密切相关。此高阶项虽然在数学推导中存在，但是算例分析表明，此高阶项的数值相对于低阶项而言较小，因此可以忽略。在中国稀缺定价机制设计中，建议根据各地实际情况，计算此高阶项的数值，若数值相对不大，可参考得克萨斯州将备用价格增量的高阶项忽略。

后续研究将分析备用价格增量高阶项的实际物理意义，并设计相应市场规则。此外，算例只分析现货市场结果，后续可进一步针对长时间尺度下的ORDC 模型进行仿真分析，并与容量市场机制对比，以期对中国下一阶段电力市场及配套容量机制的建设提供一定的借鉴意义。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。