海水淡化双级真空引射器的射流和混合特性研究

2021-03-30苏闯建张凤鸣陈顺权

集成技术 2021年2期

苏闯建张凤鸣,2* 陈顺权* 莫明吴彤

1(广州中国科学院先进技术研究所广州 511458)2(中国科学院深圳先进技术研究院深圳 518055)

1 引言

近年来，我国的淡水资源短缺问题不断加剧，而海水淡化是解决水资源短缺的重要途径[1]。海水淡化是指将海水经过脱盐处理转化成淡水的过程，当前主流工艺主要分为膜法和热法。低温多效蒸馏是“热法”海水淡化的主流技术，具有淡水水质好、过程循环动力消耗低、对海水预处理要求不高等突出优点，可利用低品位能源作为热源，具有广阔的应用与发展前景[2]。

低温蒸发需要在负压条件下实现，而现有蒸馏器一般通过机械真空泵或引射器来实现装置的真空度。其中，引射器本身没有机械传动元件，结构简单，便于制造和拆解维护，具有耐磨损、无需润滑保养和使用寿命长等优点，已得到广泛应用[3]。引射器的工作原理是压力不同的两股介质间进行质量交换、动量交换和能量交换后，混合流体以相对居中的压力经扩压管增压后排出。两股流体中压力较高者称为工作流体，压力较低者称为引射流体[4-5]。单级引射器已广泛应用，但因其只形成一次射流卷吸，单一真空度的特点难以满足多点真空度的工艺要求。而相较单级引射器，双级引射器具有调节功能，其潜在应用价值更为广阔。因此，本文作者团队研究设计了应用于海水淡化系统的双级引射器[6]，并应于船用单效海水淡化装置中，大大降低了海水淡化装置的能耗[7]。上述研究主要是为了实现两级抽吸作用，但均未涉及双级引射器间的抽吸速率、极限压力、不同相组分的差异性，进而无法适应不同工艺过程对双级引射器的差异化需求，同时也限制了双级引射器的进一步推广应用。

通过数值模拟研究引射器内部流场状态是降低能耗并实现装置调控的重要手段[8-9]，但目前关于双级引射器的研究仍较为缺乏。裴文伟等[10]、粟海锋等[11]采用两相流模型推导出双级液气引射器喉管的特征方程；陆东宏[12]研究变黏度、变密度流体对引射系数的影响；冯东东等[6]、薛浩渊等[13]则关注过程参数对真空度的影响规律。上述研究大多通过二维简化模型对引射器进行性能分析和优化，缺乏对引射器内部流动和传输特性的研究，无法真正实现引射器的调控和节能降耗。因此，本文采用三维数值模拟来分析引射流体和工作流体的混合及扩散过程，探索降低能量损失的方法，为引射器的应用奠定基础。

2 装置与主要尺寸参数

与单级引射器结构和原理类似，双级引射器(图 1)由一级吸入室、一级引射口、一级喷嘴、二级吸入室、二级引射口、二级喷嘴、混合室、扩散室八个部分构成，其几何参数见表 1。

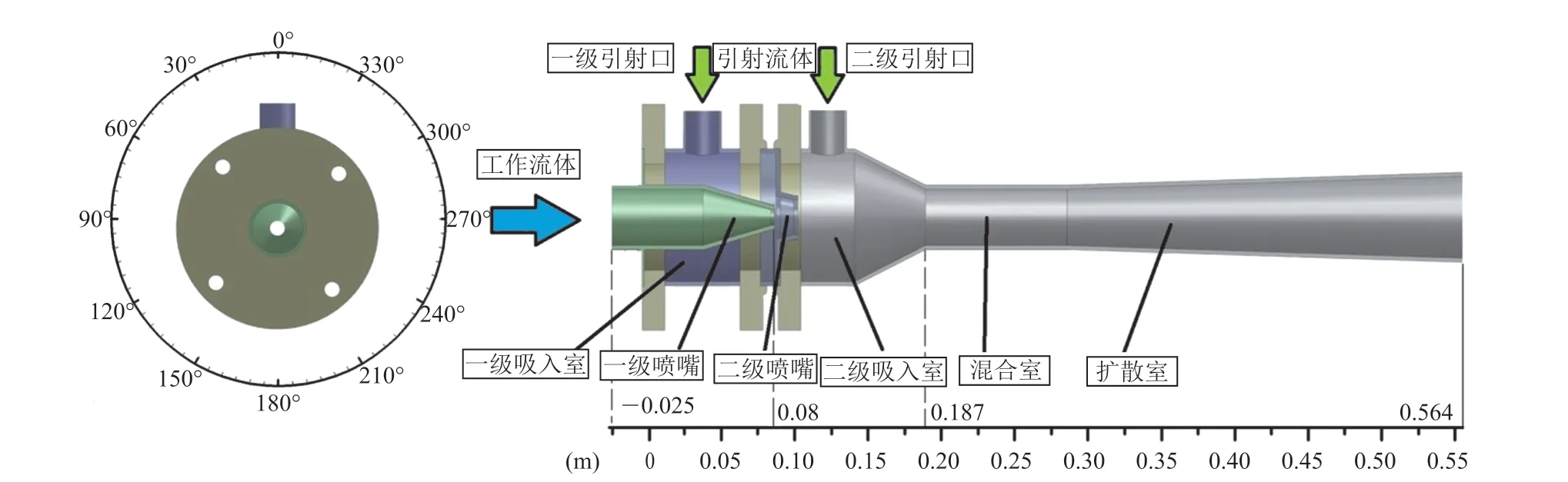
图1 双级引射器结构图Fig. 1 Structural diagram of the two stage ejector

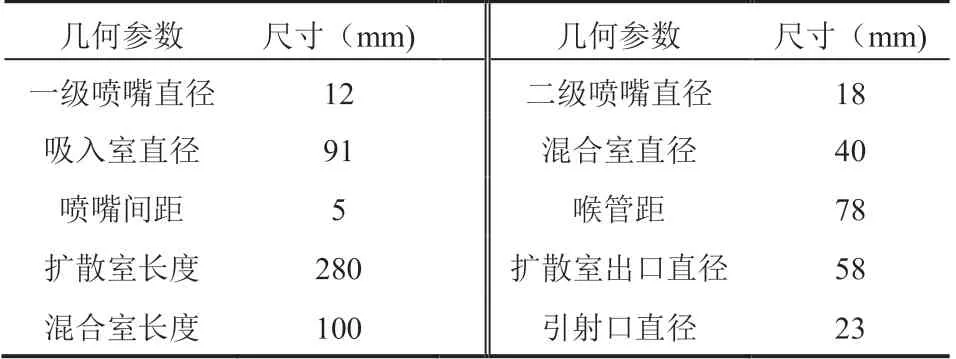
表1 双级引射器主要几何参数Table 1 Geometric parameters of the two stage ejector

双级引射器与单级引射器的不同点在于，其产生两次真空度、两次引射：工作流体流经一级喷嘴时，其绝热膨胀后的高速流体使一级喷嘴出口处形成负压，此时一级引射流体因为压差于一级引射口流入，与工作流体混合后经二级喷嘴于二级喷嘴口形成二次负压；随后二级引射流体由于压差流入二级吸入室与一级混合流再次混合，经混合室混合充分后，由扩散室增压后高速喷出。

3 模拟方法与设置

本文采用 Fluent 软件对双级引射器进行三维数值模拟，控制方程包含稳态的连续方程、动量方程和能量方程。采用 k-ε 双方程湍流模型与标准壁面函数，以及压力和速度耦合的 SIMPLE 算法。边界条件根据试验测定值设置，工作液体入口设置为速度入口，引射流体入口边界设置为速度入口，出口边界设置为压力出口。引射流体可为气体和液体。考虑到模型的简化，本文首先采用单相流动模型研究两吸入口均为液体的双级引射器的流动混合特性。模拟过程中，各流体介质均为常温纯水。

由于紧靠管道壁面的区域内压力梯度和速度梯度较大，而靠近管路中心较小，除一级与二级吸入室部分外，在靠近管壁处均采用较密的边界层网格。考虑从喷嘴射出后的湍射流结构，在二级喷嘴到出口处进行分区域划分网格。其中，从工作流体入口段到一级喷嘴、一级喷嘴到二级喷嘴、二级喷嘴一直到出口段的内部区域，这部分流动区域形状规则，采用计算速度快的结构网格进行网格划分，并在射流剪切层进行了局部加密。其他区域则采用非结构网格中适应性比较强的混合网格进行划分(图 2)。

图2 引射器网格图Fig. 2 Mesh for the ejector

为了降低模拟结果的误差，本文首先对网格独立性和模拟模型的验证进行了研究。由于能量守恒原理和一、二级吸口的相互抑制作用，不同的网格数对应的一级、二级真空度结果也略有不同。如图 3(a)所示，一级真空度峰值为 101.0 kPa，低值为 98.3 kPa。二级真空度峰值为 77.1 kPa，低值为 63.3 kPa。由此可见，网格数对一级真空度的影响很小，而对二级真空度影响较大。从图中数据趋势可看出，当网格数大于 80 万后，对真空度影响非常小。考虑计算能力，此次模拟的网格数约为 80 万。

图3 模型验证Fig. 3 Model validation

此外，本文通过对比试验和模拟的两级吸口真空度数据来验证三维模拟模型[6]。如图 3(b)所示，随着入口速度的提升，两级吸口的试验和模拟数值变化趋势是保持一致的。但由于一、二级吸口的相互抑制作用，模拟值与实验值的误差呈现不同的变化规律。其中，一级真空度在中高入口流速下，试验和模拟数据能够较好的对应；而二级真空度在中低入口流速下，试验和模拟数据能够较好的对应。但总体而言，除个别运行参数外，模拟和实验误差一般小于 10%，表明三维数值模拟模型能较好地预测双级引射器。

4 结果与讨论

4.1 射流扩展特性

4.1.1 沿程压力与速度分布

图 4(a)显示，射流速度在入口段与二级喷嘴出口处(x＝0.1 m)快速下降，进而形成负压。图 4(b)显示速度于二级喷嘴出口处(x＝0.1 m)至二级吸入室出口处(x＝0.2 m)明显下降，而混合流体流入混合室后，混合流体速度与压力不再明显下降。此外，图 4 中的压力分布趋势与速度分布趋势相反，符合能量守恒定律。本文作者课题组前期研究引射器的速度及压力云图结果表明：喷嘴直径与工作流体流速是影响喷射器内部负压大小的主要因素[6]。这主要源于工作流体速度越大，喷嘴直径越小，形成的湍流传递给引射流体的动能越多，负压越低[14]。而在相同工作流体流速下，引射流体流速从 0 m3/h 增加至 4.5 m3/h 时，吸口对应中心的负压呈现先增加后减小的趋势。主要原因是引射器的引射系数限制，超出引射流体流速范围，相应的真空度会迅速降低[6]。

4.1.2 径向速度分布

图 5 显示速度从喷嘴中心沿径向急剧下降，而喷嘴内轴线区域(径向距离约为 0.01 m)的径向速度最大，这也对应轴线处的流体湍动程度大而近壁面流体湍动程度小。这主要源于流体由喷嘴喷射后与周围流体产生黏性压差，从而形成混动边界层，流体在混动边界层内进行动量及质量传递[15]。此外，引射流体流速的变化对一、二级喷嘴轴线区域影响较小，其主要影响在近壁面处。随着引射流体流速的增加，大体呈现逐渐增加的趋势。

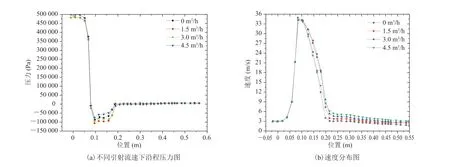
图4 (a)不同引射流速下沿程压力与(b)速度分布图(工作流体流速为 2.85 m/s)Fig. 4 (a) Pressure and (b)velocity distributions at diあerent velocities of ejected fluid, and the velocity for working fluid is 2.85 m/s

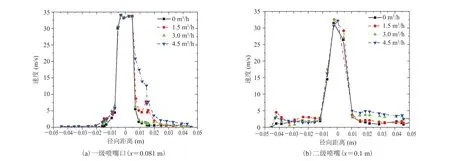
图5 喷嘴口速度沿径向分布图Fig. 5 Radial velocity distributions at nozzle outlet

图 6 为二级吸入室混合流体速度沿径向分布。通过对比发现其共同点为，靠近壁面处(径向距离在 0.02～0.04 m)的速度均呈现上升后下降趋势。其原因为，流体于吸入室内产生漩涡，流体湍动程度加大。而随径向距离的增大，流体近壁面处速度增加幅度更大，此时，压力开始回升，流体涡旋现象明显。而在中心轴线附近，无旋涡影响的流体速度沿远离喷嘴位置逐渐降低。当混合流体流经混合室并经过二级喷嘴后，流体处于高压高速状态。此时流体混合均匀，近壁面处流体漩涡现象不明显，如图 6(d)所示，速度无上升段，而流体的湍动态则在轴线处表现明显。引射流速的变化在吸入室对旋涡起到先加强后降低的作用，而在混合室，速度则取决于总混合流体的流量。

4.2 混合特性

4.2.1 吸入室流动迹线分析

为更直观地分析引射器内部的混合过程，图 7 为分别以一级吸口和二级吸口的角度(图 1)截取吸入室内流体流动迹线。从图 7 可知，流体在喷嘴内以及混合室内流线均匀，而在吸入室引射口处产生旋涡且在吸入口处产生一个或多个旋涡。现有研究表明，旋涡的产生一方面增大近壁面处的流体速度，不利于混合流体流动；另一方面，旋涡致使流体在吸入室内消耗更多能量，导致泵的运行效率低下[16-17]。由此可知，一级吸入室主要产生多个小的旋涡和二级吸入室产生大旋涡可分别对应图 6 的速度径向分布规律，也相应解释了二级吸口近壁面的流体流速增加幅度较大及真空度下降。

图6 吸入室及混合室速度沿径向分布图Fig. 6 Radial velocity distributions of suction chamber and mixing chamber

4.2.2 吸入室截面压力云图与混合迹线分析

如图 8 所示，随着入口速度的提升，引射压力和流动轨迹呈现多样的变化规律。不同的引射流体速度所展现出的压力分布与流动轨迹的共同点在于：混动迹线都是不对称分布，且不对称性随引射流体速度的增大而增大。这表明，在吸入室内，流体流动并非二维，因此通过二维数值模拟无法掌握引射器内部的混合特性[6,15]。王松林等[18]通过对喷嘴及吸入室截面流线图分析发现，喉管二次流动速度小于主流(轴线方向)速度。因此通过图 8 可知，由于涡流促使流体径向速度增大，流体处于三维流动状态，但其主要流动方向是沿中心轴线，故可将流体在吸入室内的流动状态近似看作二维流动。

不同的引射流体速度所展现出的压力分布与流动轨迹的不同点在于：随着引射流体速度的增大，负压先增大后减小。其原因在于，当较小的引射流体流速与工作流体混合时，能量损失较大。而当引射流体速度较大时，其混合时间短，能量损失较小。从图 8 可看出，当引射流体速度足够大时，其漩涡量较少且漩涡较小。因此，为改善泵运行效率，可适当提高引射流体速度。

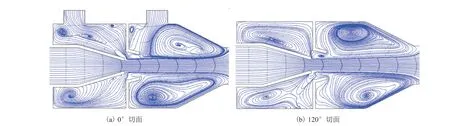
图7 吸入室切面流线图Fig. 7 Streamline diagram of suction chamber section

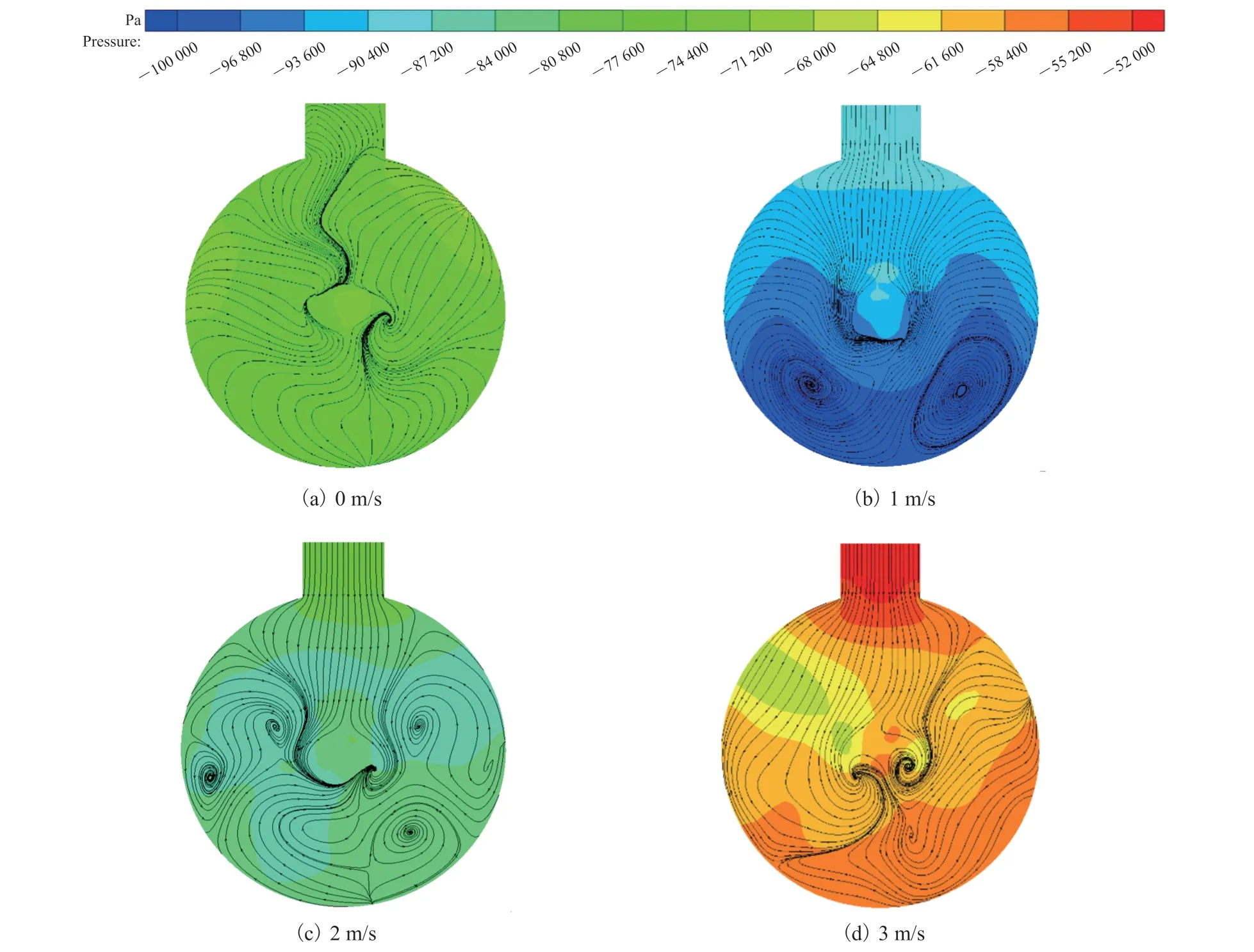
图8 不同引射流速度下的吸入室截面压力云图Fig. 8 Pressure contours of suction chamber section under diあerent jet velocities

4.2.3 湍动耗散率与湍动能

为分析不同径向位置的流动和混合特性，通过无量纲参数 L/R 表征径向位置(其中 L 为偏离喷嘴中心的距离，R 为喷嘴半径)，分析湍动能(湍流强度)和湍动耗散率(分子黏性作用下由湍流动能转化为分子热运动动能的速率)的变化规律。图 9 显示不同 L/R 的湍动耗散率分布规律大致相同，均呈现先增大后降低的趋势。随着 L/R 比率的增大，曲线向左平移，湍动耗散率峰值由二级吸入室向二级喷嘴移动。而湍动能最大值(图 10)则发生在二级吸入室。当 L/R＝1 时，湍动耗散率在一级喷嘴急剧上升后下降，在二级喷嘴再次达到峰值，而湍动能在一级喷嘴较小。因此，在此比率下，流体在一级喷嘴里的湍动力度较小。此外，引射流速对不同径向位置湍动能和耗散率的影响是不规律的，这主要取决于旋涡的形成与分布。

对比图 9 与图 10 可知，湍动耗散率最大值处与湍动能最大值处大致一样。而在吸入室内，湍动能主要是传递给大涡流。随着 L/R 的增大，湍动耗散率明显增大，而湍动能只略微增大。随着 L/R 比率的增大，湍流能量耗散速度增大，漩涡消散得更快[19-20]。

4.3 讨论与分析

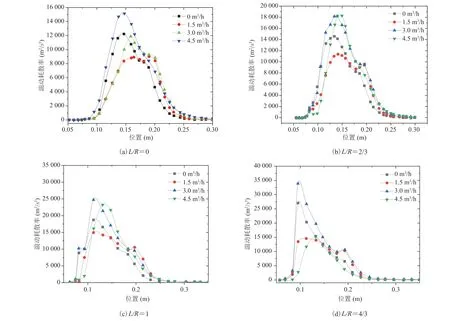
图9 湍动耗散率图Fig. 9 Turbulent dissipation rate

本文在前期双级引射器二维数值模拟获取压力和温度分布的基础上[6]，通过建立三维数值模拟模型，获取速度、压力、流线、湍流、旋涡等参数的三维分布，进而分析引射器的射流和混合特性，为后续双级引射器的优化设计奠定了基础。相比单级引射器及本文作者课题组前期的研究工作，流场特性既体现一些类似规律，但又展现出一些重要特性。首先，工作流体的射流卷吸作用进而形成真空效应在单级或双级引射器、二维或三维模拟的规律是一致的[14]。而另一方面，通过三维模型方可洞悉引射器内的流线和旋涡分布，进而对应解释一、二级吸口真空度的变化规律。此外，本研究可掌握引射速度对湍动能和耗散率的影响规律，结合旋涡的形成和分布，为后续掌握一、二级吸口的相互作用提供指导。

图10 湍动能Fig. 10 Turbulent kinetic energy

当然，本文也存在不足之处，需要在后续研究中进一步补充及完善。首先，在计算模型上，本文采用单相流模型对纯水介质在双级引射器内的射流混合特性进行模拟。而实际应用过程中，气体也常常出现在引射流体中。可凝结和不可凝结气体对射流混合、真空度都会产生重要影响。因此，建立符合双级引射器的两相流模型将是后续研究的关键。其次，工作流体和引射流体间也常常存在温差，需要考虑能量方程对两相流模型的影响。最后，双级引射器的重要特征是两级引射口的相互抑制，掌握双级引射器的射流和混合特性是协调两级吸口引射作用的关键。为了进一步掌握双级引射器间的相互作用关系和协调机制，需要在本文的基础上系统研究两级喷嘴尺寸、间距、喉管等结构和运行参数对流动和混合特性的影响规律。