基于高功率电磁脉冲的深海脉冲声源仿真和实验研究

谢晋兴 张永亮 江 敏 江 彪 郑江龙 刘 丹 王宜志 黄逸凡*

1(中国科学院深圳先进技术研究院 先进材料科学与工程研究所 深圳 518055)2(南方科技大学 海底地震仪设备与技术工程实验室 深圳 518055)

1 引 言

水声是水下信息传播最有效的媒介，因此发展水声传感及探测技术是认识海洋的必然手段。水下声源的不同工作频段在水下探测方面存在较大差异，其核心部件——发射换能器在水声探测系统中至关重要。以海底探测为例，侧扫声呐的工作频段一般在数百 kHz，多波束声呐主要工作在数十 Hz，两者都用于海底地形地貌测量，可以得到分辨率很高的精细海底图像，但无法得到海底以下的信息，主要原因是高频声信号在海底沉积物中吸收衰减很快[1]。浅剖声呐工作频段相对较低，一般在数 kHz 左右，可以穿透数米左右的海底地层，得到最高分辨率在 20 cm 左右的地层剖面[2]。参量阵声源也可以获取类似的地层信息，但不同于线性声源，参量阵产生数十 kHz 左右的双频信号，利用远场非线性作用得到数 kHz 的差频信号[3]。浅剖和参量阵声呐主要用于海底浅层埋藏物探测。如果要获取更深的海底地层信息，那么需要使用频率更低的声源，如电火花声源(Sparker)、电磁脉冲声源(Boomer)等。Sparker 和 Boomer 产生的是高功率脉冲波(又称地震子波)，主频一般在数百至数千 Hz 左右，结合单道或多道接收系统进行地震勘探，可以获得最高分辨率 1 m 左右、穿透深度达到数十米至数百米的地层剖面，因此在工程地质调查、海底浅层资源调查方面应用广泛[4]。

常规的海底测绘或者地震勘探都采用水面作业形式，调查设备通过调查船在海面拖曳进行巡线作业。对于深海水域，受菲涅尔半径限制，常规作业无法获得较高探测分辨率[5]，因此国内外多个研究机构都开展了深拖浅剖或深拖地震系统等方面的研究。在深拖浅剖方面，美国 Benthos 研制了一套 3 000 m 级的深拖浅剖系统 SIS3000[6]，我国大洋号远洋调查船装备了此系统。中国科学院声学研究所也研制了类似的深拖系统 DTA6000[7]。深拖地震方面，美国 NRL(Naval Research Laboratory)在 20 世纪 90 年代研制了一套 6 000 m 级的深拖地震系统 DTAGS[8]，法国 Ifremer 在 21 世纪初也研制了类似的系统 SYSIF[9]。我国海洋一所依托“十三五”重点研发计划深水专项研制了2 000 m 级的深拖地震系统“揆洋号”，目前正在海试过程中[10]。

综上所述，由于不断追求提高探测分辨率，深海探测活动逐渐增多。不同于常规水面声源，深海声源需要克服深水环境的高水静压做功，对换能器材料、结构设计等方面的要求较高。以深拖地震为例，深水环境下的高功率低频地震子波发射是需要解决的技术难点。美国 DTAGS 和法国 SYSIF 都采用赫姆霍兹共振腔(Helmholtz Resonator)类型的发射换能器，其特点是换能器效率高，发射的调频信号经过解调得到的子波脉冲窄、频带宽，有利于提高成像分辨率，但换能器及其功放系统庞大[11]。我国哈尔滨工程大学[12]、上海船舶电子设备研究所等[13]也在开展深海共振腔声源的研究。与此二者不同的是，自然资源部第一海洋研究所牵头研制的“揆洋号”采用了电火花结构作为震源，其特点是换能器发射地震子波，无需解调处理，且功放和换能器都相对较小，但换能器寿命较短，需要定期维护。因此，研制工作性能(声源级和主频)受水静压影响小，工作寿命长，且方便深拖系统搭载的高功率脉冲声源对于近海底地震勘探是至关重要的。本文基于高功率电磁脉冲机理研发深海脉冲声源，通过建模仿真和实验测试深入研究高功率脉冲电路、换能器的线圈负载、脉冲电流激励的电磁力、磁力驱动的发射板在空气介质和水介质中的振动，以及不同水静压条件下发射板的振动特性等关键基础问题，为深海脉冲声源的研发提供基础数据支撑。

2 方 法

2.1 计算模型

本文将电磁脉冲换能器简化为两部分：线圈负载和发射板。模拟仿真也主要从两方面开展：脉冲激励的电磁力和电磁力驱动的发射板振动。使用的模拟软件为 Comsol 多物理场耦合计算软件，模拟的参数包括脉冲电流、电磁力和发射板振动(位移)等，同时使用 Matlab 进行辅助数据分析，特别是对实验视频记录的图像处理、轨迹捕捉以及利用位移数据计算速度和加速度等。

2.1.1 电磁力计算模型

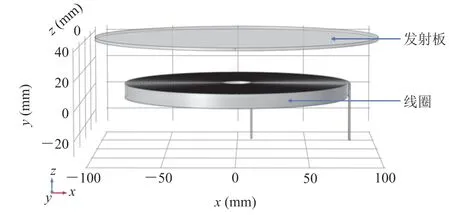
图1 用于电磁力计算的几何简化图Fig. 1 Simplified geometric diagram for electromagnetic force calculation

线圈激励使用电压激励如图 2，激励函数是以 t 为变量的阶跃函数 step1(t)。根据实际实验参数，step1(t)的高电平为 1.6 kV，低电平为 0 V。同时，放电开关设置触发时延 50 μs，系统整体延迟 25 μs，因此设置阶跃函数过渡区宽度 75 μs，阶跃起始点取过渡区宽度的一半，即从 37.5 μs开始。

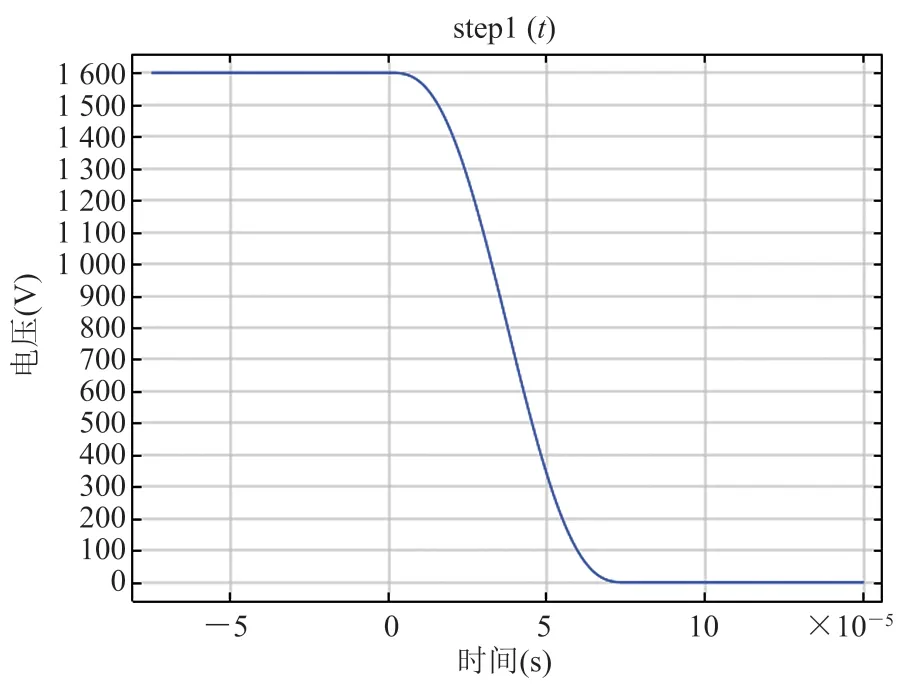
图2 电压激励波形Fig. 2 Voltage excitation waveform

其他在磁场模块设置的参数包括：空气的电导率为 1 S/m，铜的电导率为 5.998e-7 S/m，发射板的电导率为 3.774e-7 S/m；同时非铁磁性材料相对磁导率均接近 1，为简化计算节省时间，均设置为 1。研究方法方面选用瞬态研究，采用广义 α 方式求解。原因是广义 α 相对于向后差分法具有更小的阻尼，处理突变参数的计算更准确，对于结构力学、声学和瞬态电磁波等对过度耗散敏感的物理模型来说，广义 α 是最佳选择。

2.1.2 振动计算模型

由于振动模拟使用三维模型的计算量大、耗时长，通常一次三维模型运算需要数百分钟，而简化二维模型仅需要数分钟，相差悬殊，且随着精度的提高，三维模型耗时呈指数增加，因此本文设计二维模型作等效替换。具体地，设置二维模型与三维模型采用相同的电压脉冲激励，并调校二维模型使输出相同的时域电流波形、电磁力波形。在此，本文认为二维模型可以作有效替换，二维轴对称结构如图 3 所示。几何等参数设置与计算电磁力的三维结构相同。此外，物理场使用磁场(Magnetic Field)模块作电磁转化计算；运动过程使用全局微分方程(ge)模块作位移计算；模型中结构运动表达使用动网格(ale)模块。

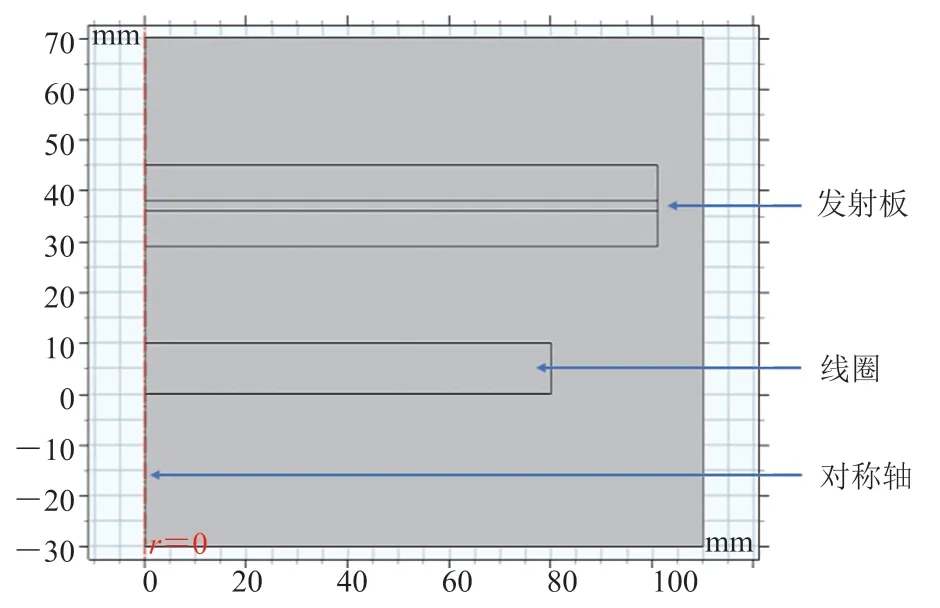
图3 用于发射板振动计算的轴对称几何结构Fig. 3 Axisymmetric geometric diagram for emitting plate vibration

发射板在受迫运动过程中主要受以下几个方面的力作用：随位置变化的电磁力 Fmf，随位置变化的弹簧阻力 Fr，随速度变化的介质阻力 Fra。因此，全局变量方程中设置速度 v 的函数如下：

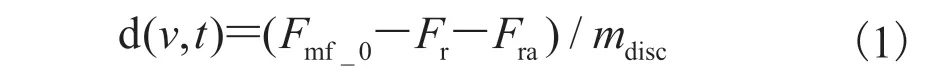
其中，mdisc＝0.173 kg，为发射板的质量；Fmf由电磁力模型计算得到；Fr和 Fra的具体计算公式如下：

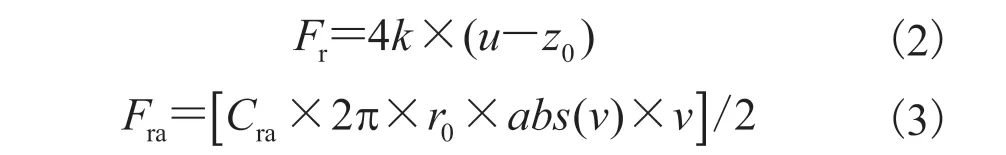
其中，k＝970 N/m，为弹簧弹性系数；u 为发射板瞬时位置，mm；z0为发射板初始位置，mm；Cra为阻尼系数(这里将水阻力与弹簧阻尼进行等效计算)，N·s/m；v 为发射板瞬时速度，m/s。此外，公式(3)使用 abs(v)×v 来表示 Fra为矢量。

学习仅仅是计算机科学中的一个专门术语，用更为严格的数学语言来说，学习即是统计的意思。机器学习，简单地说，仅仅是利用计算机这个平台，利用统计学的方法，去对数据集进行分析与归纳。现代个性化的推荐系统便是机器学习中的一个重要的主题，也是我们日常生活中较为熟悉的一个机器学习的贴切的例子。推荐算法是推荐系统的核心所在，一个特定的算法本质上就是一个计算的过程。推荐算法的计算主要来自于数学中的线性代数与概率统计，其中一个核心的概念，便是矩阵。

2.2 实验设计

本文设计了一套实验系统对脉冲电流、发射板振动等参数进行实际测量，验证模型计算结果的准确性。实验系统包括研制的脉冲电源、电磁脉冲换能器、高压水舱以及电流互感器、示波器、高速相机等测量设备。

脉冲电源的研制采用基于高频全桥逆变和复合半导体开关的脉冲电路，电路原理如图 4(a)所示。其中，脉冲储能采用容值 40 μF，耐压 3.5 kV的电容器。电容器充电采用工作频率 40 kHz 的半桥逆变电路将输入直流转换成高频交流，经谐振、升压整流后形成直流高压。电容器最高充电电压设定 1.6 kV，因此单脉冲放电能量 51.2 J，且实验过程中固定放电能量不变。放电开关采用由可控硅和续流二极管组成的复合开关模块。模块开关耐压 3.6 kV，允许浪涌电流(10 ms)达到 10.5 kA。电路实物如图 4(b)所示。

图4 脉冲电源电路Fig. 4 Pulse power circuit

电磁脉冲换能器的线圈负载采用截面面积10 mm2的铜带绕制，与计算模型中参数一致。经数字电桥(常州同惠，TH2830)测量 1 kHz 频率下的电感为 83 μH，内阻为 152 mΩ。线圈负载采用 3M2131B 硫化胶整体硫化，同时采用耐压为 60 MPa的橡塑型水密连接件。发射板采用 2 mm 厚度的铝合金板。发射板 4 个角的两侧都安装有弹性系数为 970 N/m 的弹簧。换能器实物如图 5 示。

在脉冲电流测量方面，本文采用美国 Pearson 4418 电流互感器，灵敏度(1±1%)mV/A，带宽 0.7 Hz～2 MHz，可测量峰值电流 200 kA，最快前沿 200 ns。测量脉冲电流的同时，电容电压通过美国泰克 P6015A 高压探头进行采样，衰减比 1 000∶1，带宽 75 MHz，可测量直流电压峰值 20 kV。电流电压信号由示波器(美国泰克，TBS1102)进行显示和采集。

图5 电磁脉冲换能器实物图Fig. 5 The electromagnetic pulse transducer

在发射板振动测量方面，本文分别在空气介质和水介质中进行实验。其中，空气介质条件下的发射板振动测量实验系统如图 6 所示，高速相机(日本 NAC，MEMRECAM HX-7s)正对电磁脉冲换能器的纵截面，以帧率 2 000 fps 记录发射板的振动过程。脉冲电源通过触发线与高速相机相连，同步相机采集信号。

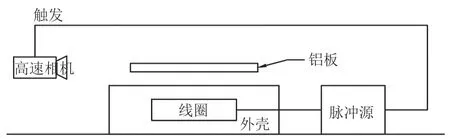
图6 发射板振动测量实验系统示意图Fig. 6 Schematic diagram of experimental system for plate vibration measurement

水介质中的发射板振动实验在高压水舱中进行。高压水舱内径 200 mm，有效深度 500 mm，在舱体中部有一对对称的观察窗，最高工作压力为 120 MPa，舱体结构与实物如图 7 所示。将脉冲源外置，发射头通过嵌于舱盖的耐压水密接头与脉冲源连接，发射头竖直放置，盖好打压后通过观察窗记录发射板位移情况。测量方法与空气介质实验一致，在其中一侧的观察窗架设高速相机，另一侧观察窗补光照明。

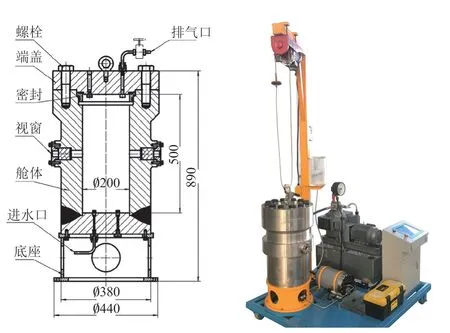
图7 120 MPa 高压水舱Fig. 7 120 MPa high-pressure water tank

3 结果与分析

3.1 放电电流与电磁力

基于 Comsol 软件，采用图 2 所示电压激励函数对三维换能器模型进行计算，同时利用设置的全局变量探针 2 得到线圈电流曲线，并与实验测得的实际放电电流曲线进行比较。图 8 结果显示，计算数据和实验数据吻合较好。其中，实验电流峰值为 1 160 A，而计算得到的电流峰值为 1 148 A。

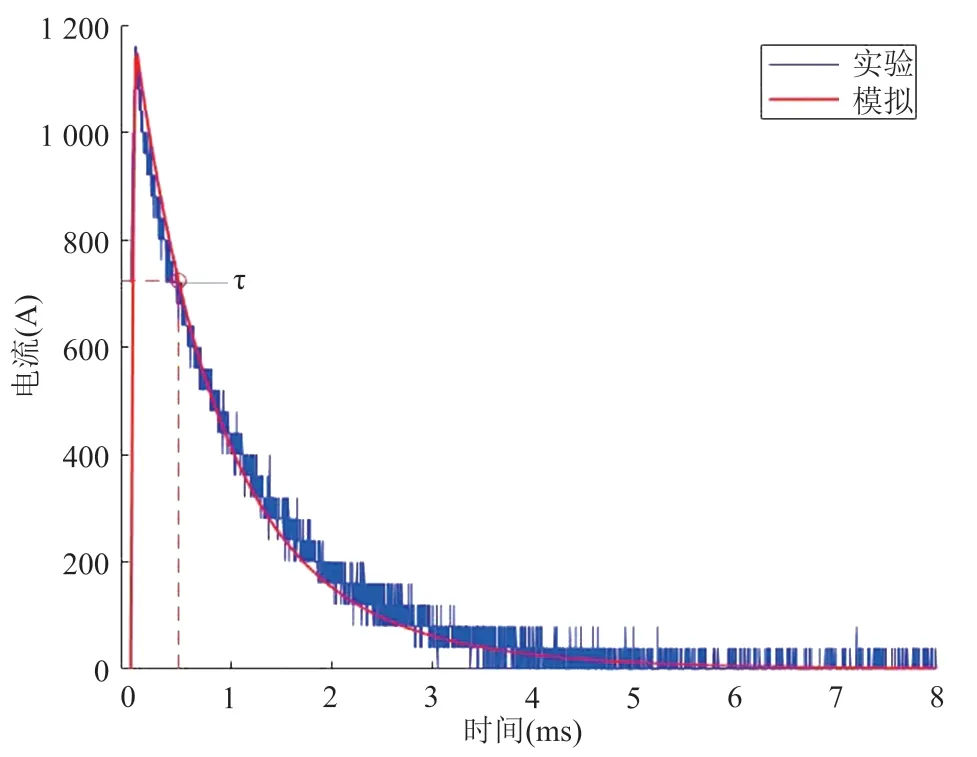
图8 放电电流的理论计算和实验结果比较Fig. 8 Simulation and experimental results of discharge current

图 8 结果也显示电流波形为单脉冲波形。本文采用的电容放电回路负载是感性负载，因此在回路中处于欠阻尼状态。为了实现单脉冲电流输出，同时也为满足与模型计算中激励阶跃函数的一致性，放电回路采用续流的电路拓扑。该电路拓扑的特点是无论放电回路的阻尼状态如何，输出电流总是单脉冲，不存在振荡，具体分析如图 9所示。首先可控硅触发打开后，储能电容通过 RLC 回路放电，其中 R 是回路中的电阻，L 是回路中的电感，C 是储能电容。此时二极管两端电压反向，处于关断状态。如果回路处于过阻尼或临界阻尼状态，那么 RLC 回路持续至电容放电完毕。如果回路处于欠阻尼状态，那么电容电压先于电流达到零点，并开始反向充电，此时二极管两端因存在正向电压而导通，回路电感储能通过 RLD 回路放电，其中 D 为续流二极管。由此该放电回路的电流输出呈单脉冲特性。

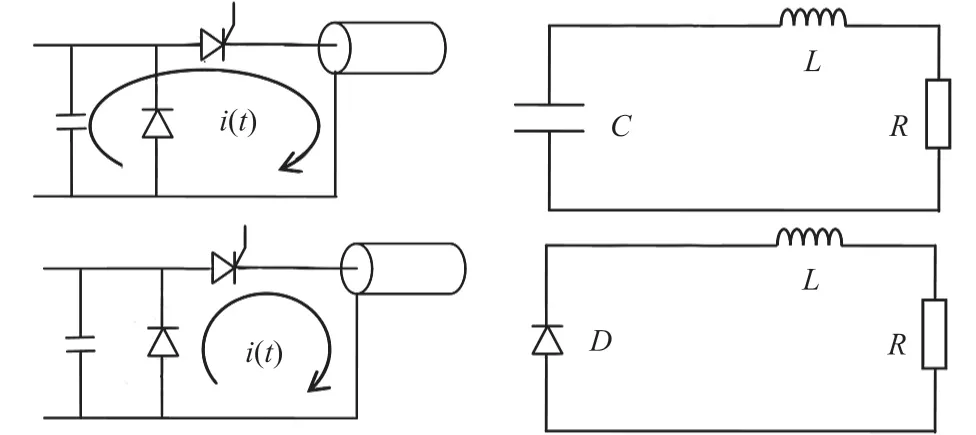
图9 放电回路的单脉冲电流输出Fig. 9 Single pulse current output of discharge circuit

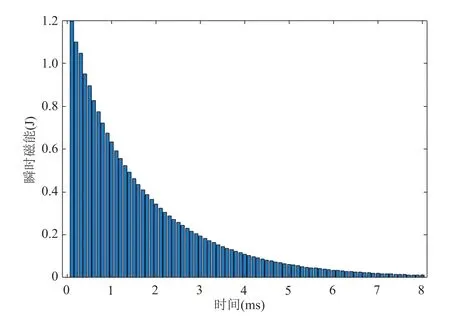
图10 线圈负载的磁能曲线Fig. 10 Magnetic energy curve of coil load

基于放电电流波形数据，利用模型中设置的全局变量探针 1 得到线圈负载的磁能，即电容储能通过线圈负载放电将电能转化为磁能。图 10 为 8 ms 时间宽度内以 0.1 ms 为单位时间的瞬时磁能分布，累加得到总磁能为 19.03 J。由于电容储能为 51.2 J，因此线圈放电产生的磁能转化效率为 37.17%。

图 11(a)为计算得到的负载线圈放电电流，图 11(b)为发射板受到的电磁力，图 11(c)比较了不同激励电压条件下的电流峰值与电磁力关系。从图结果可知，激励电压越大，放电电流越大，产生的电磁力也越大，同时电磁力的作用时间远小于放电电流的衰减时间。比较放电电流峰值(Imax)和电磁力峰值(Fmax)可知，两者呈线性相关，结果如图 11(c)所示。

图11 不同激励电压影响关系Fig. 11 The influence of diあerent excitation voltage

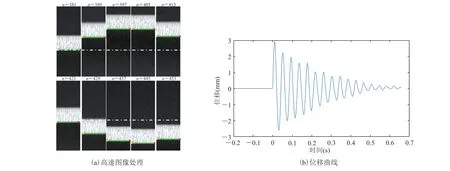
图12 发射板在空气介质中的振动Fig. 12 The vibration of plate in the air

3.2 发射板振动幅度和频率

在空气介质中，高速相机对发射板振动的记录帧速为 2 000 fps。图 12(a)为实际捕获的发射板振动图片，其中上下各 5 幅图片分别为发射板初始向上振动和向下振动，图中 n 为高速成像的帧数，上下 5 幅图片间隔帧数为 8，因此时间间隔为 4 ms。本文采用 Matlab 程序对上述图片进行处理，使用 Edge 函数进行边缘判定，其中包含 Canny 边缘检测算法。具体步骤为：先用高斯滤波器平滑图像，再使用一阶偏导的有限差分来计算梯度的幅值和方向，再次对梯度幅值进行非极大值抑制，最后用双阈值算法检测和连接边缘。这里设置 Canny 参数值为 0.5，对发射板下边缘进行霍夫变换后取得直线(绿色)，同时以发射板厚度 2 mm 作为参照尺度，根据像素变化对其振动的位移量进行计算，结果如图 12 所示。

发射板在电磁力和弹簧等共同作用下的振动特性为周期阻尼衰减，其中主要原因是根据图 11 的电磁力曲线，电磁力作用时间仅 0.8 ms 左右，远小于弹簧和发射板构成谐振系统固有周期约 42 ms。在电磁力计算数据的基础上，根据公式(1)、(2)和(3)可以得到发射板振动的计算数据，与实验数据的结果比较如图 13 所示。发射板振动幅度和频率的计算结果与实验数据吻合较好，实验测得发射板的振动幅值达到 2.97 mm，计算得到的最大振幅为 2.93 mm；实验频率为 23.84 Hz，模拟频率为 22.89 Hz，误差 3.98%。

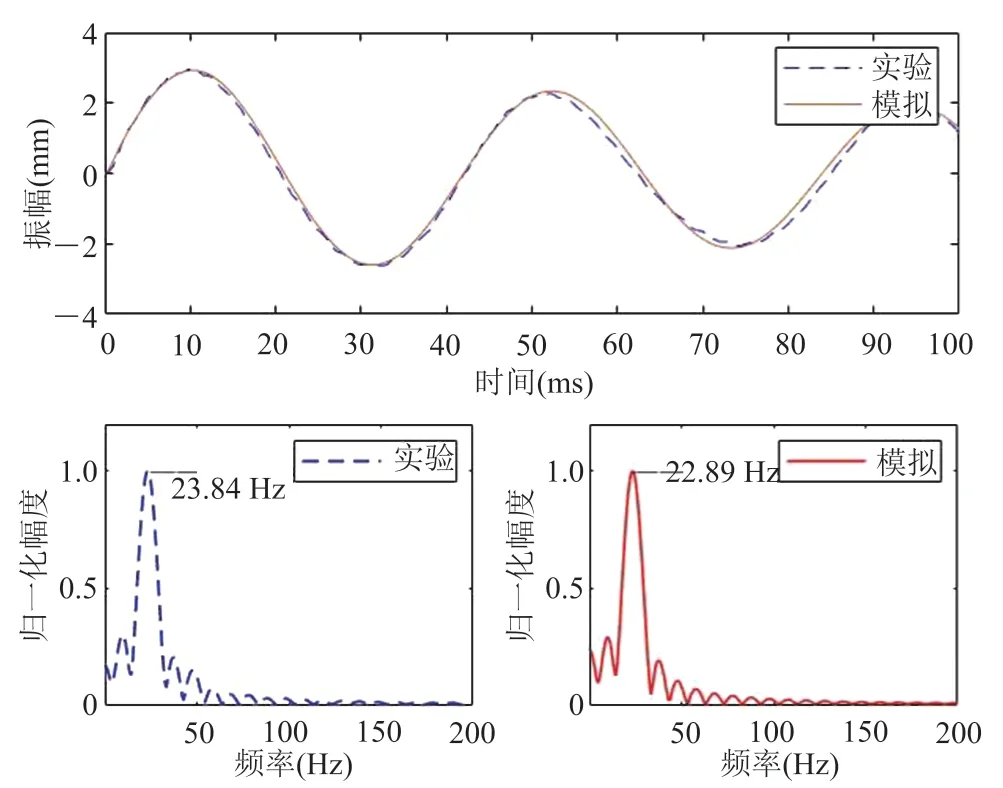
图13 发射板振动位移和频率的理论计算与实验比较Fig.13 Calculation and experimental comparison of the plate vibration displacement and frequency

图14 高压水舱内的发射板振动高速成像Fig. 14 High speed image of plate vibration in high pressure water tank

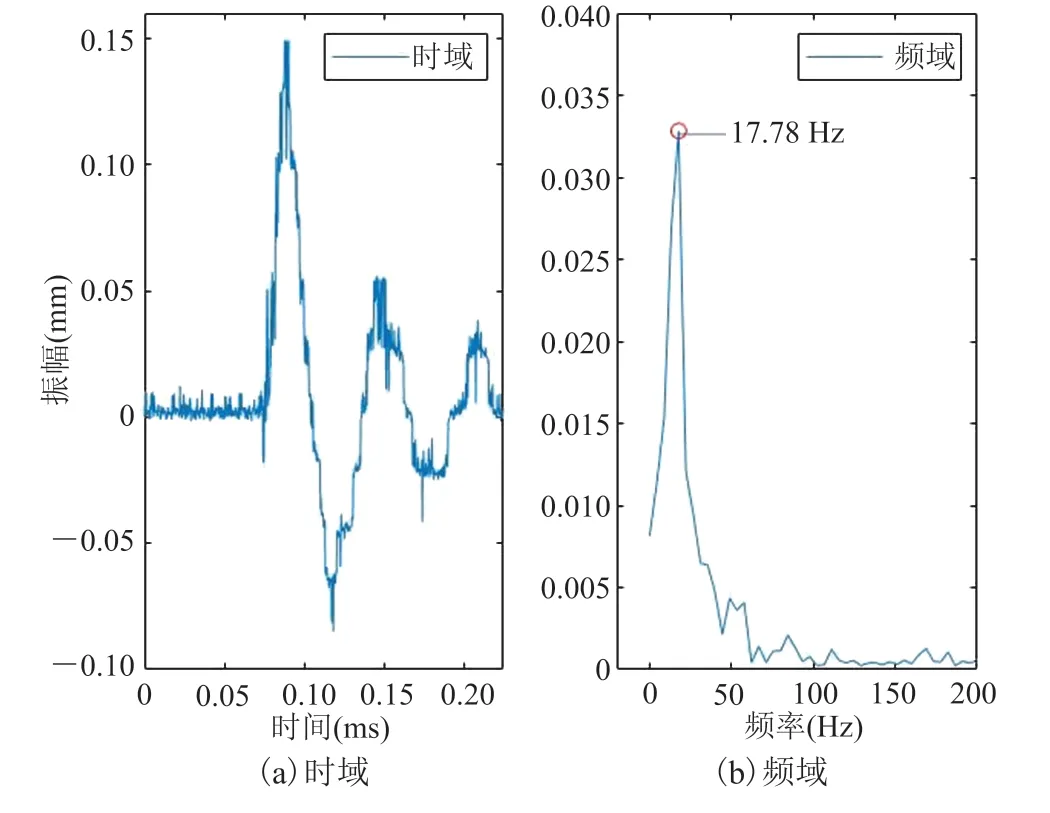
图15 10 MPa 震动情况Fig. 15 Vibration under 10 MPa pressure

图 14 为 10 MPa 水静压下水介质中高速相机记录的发射板振动图像。其中，图像处理方法、相机帧速等实验参数与空气介质相同。图中上侧黑色部分为发射板，以其厚度 2 mm 做标尺计算发射板的位移量，下侧黑色部分为发射头外壳，白色部分为间隙。根据高速成像结果计算得到的发射板振动位移量曲线如图 15 所示。水介质中的发射板振动幅值为 0.15 mm 左右，远小于空气介质，同时振动的频率为 17.78 Hz，接近于空气介质，主要原因是水介质的阻尼系数远大于空气介质，发射板振动过程中受到的介质阻力比较大。

图 16 为不同水静压条件下的发射板振动幅值和频率特性变化。水静压参数分别为 0.1 MPa、10 MPa、20 MPa、30 MPa、40 MPa 和 50 MPa。从图 16 可知，发射板振幅随水静压的增大而逐渐减小，但减小的幅度不大，从 0.1 MPa 的 0.159 mm 下降到 50 MPa 的 0.135 mm，同时振动频率稳定不变。

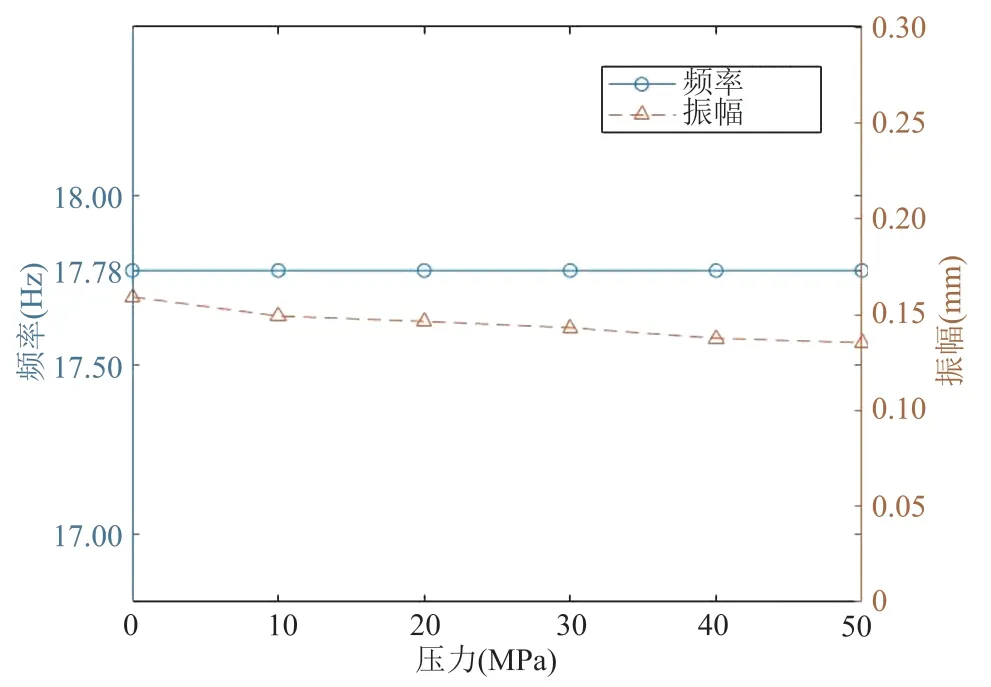
图16 不同压力条件下的频率和振幅趋势Fig. 16 Frequency and amplitude trends under diあerent pressure conditions

4 讨论与分析

国内外对基于电磁脉冲的水下高功率脉冲声源的研究较少。美国 MIT(Massachusetts Institute of Technology)在 20 世纪 60 年代对此类声源开展了初期研究，并应用于海洋地震勘探，研制了激发能量达到 1 000 J 的电磁脉冲声源(震源)系统，在浅海获得了海底以下 1 000 m 的沉积地层信息，同时也指出该类声源在深海应用的技术局限性，即发射板瞬间位移形成的空化效应[14]。同时期，中国科学院声学研究所也开展了类似的研究，同样研制了激发能量 1 000 J 的脉冲声源系统，1 m 处峰值声压级约 220 dB[15]。中国科学院声学研究所在 2015 年又研制了小型化的高功率电磁脉冲声源，激发能量 360 J，1 m 处峰值声压级达到 226 dB。目前，此类声源主要应用于海洋地震高分辨率地震勘探，且以水面(即常压环境)作业为主，已形成多个商业化产品，如英国 GeoAcoustic 公司的 GeoPulse Boomer，英国 AAE 公司的 AA251 Boomer 等，法国 SIG 的 ENERGOS series 等，具体如图 17 所示。

图17 用于水面地震勘探作业的电磁脉冲声源Fig. 17 Electromagnetic pulse sound source at water surface for seismic exploration

在深拖电磁脉冲声源方面，相关研究更少。Simpkin 等[16]报道了经过压力补偿的深拖电磁脉冲声源的波形和频谱分析结果。英国地质研究所曾研制拖曳深度达到 1 000 m 的深拖电磁脉冲声源，应用于最大深度 1 500 m 的海底地质调查[17]。此外，加拿大 GeoForce 公司推出的 DTS boomer 最大工作水深 500 m(见图 18)；Rebesco[18]也曾使用 HUNTEC 公司的深拖电磁脉冲声源进行海底地质勘探，但最大拖曳深度只有 100 m。除了上述深拖电磁脉冲声源外，未见有更大工作水深的同类型技术研究或者产品。而本文从实验室验证了水静压对电磁脉冲激励的发射板振动特性影响很小，在理论上验证了此类声源可以工作于更大的水深深度。

图18 深拖电磁脉冲声源系统(DTS boomer)Fig. 18 Deep-towed electromagnetic pulse sound source system

5 结论和展望

本文以高功率电磁脉冲为基础研发深海脉冲声源，通过 Comsol 多物理场建模仿真、大电流测试和高速成像等手段对高功率脉冲电路、线圈负载放电电流、电流激励的电磁力、以及电磁力驱动的发射板在空气介质中的振动特性(振幅和频率)等关键基础问题进行研究，研制了单脉冲输出的高压脉冲电源和线圈负载，实现了放电电流、电磁力、发射板振动的仿真计算，并利用高速成像方法对发射板振动过程进行成像，最终用实际观测数据校验计算结果，从而验证了模型的准确性。同时，本文还利用 120 MPa 高压水舱实际测试了水静压对电磁脉冲声源性能的影响，在不同水静压条件下发射板振动的高速成像结果显示其振动幅值随着水静压的增大而略有减小，振动频率不受水静压影响，从而验证了该类换能器在深水工作的技术可行性。后续工作将进一步开展不同水介质电导率、不同线圈电学参数等条件实验，优化计算模型，并根据实验和计算数据设计深海脉冲声源样机，在条件允许下开展真正的深海试验，推动该技术的实用化。