地下钢筋混凝土拱形结构在顶爆条件下的抗爆试验

刘光昆，刘瑞朝，汪 维，王 幸，赵 强

（1. 军事科学院 国防工程研究院，河南 洛阳 471023；2. 宁波大学 冲击与安全工程教育部重点实验室，浙江 宁波 315211；3. 河海大学 安全与防灾工程研究所，江苏 南京 210098）

1 引言

目前，由于地下爆炸试验的复杂性高及耗费大，针对其破坏模式及特征方面的研究一般采用数值模拟和理论的简化分析，所得出的响应特征及破坏规律缺乏对应的模型试验验证。因此，开展地下拱形结构的爆炸模型试验对地下防护工程设计十分重要。

关于岩石介质属性在爆炸荷载下对结构破坏影响的研究方面，Lu W B 等［1］研究了爆炸荷载下岩石介质中破坏分布及发展，Deng X F［2］分析了岩石节理属性对应力波传播及隧道结构破坏的影响，发现单纯地降低结构表面峰值振动速度不能有效限制结构破坏［3］；J H Shin 等［4］通过分析结构位移等响应情况划分了保护区范围，Xu J H 等［5］梳理了围岩的应力分布与结构响应之间的关系，发现深层岩体较浅层岩体更易发生破坏，但未系统性地总结相关规律及特征。

在爆炸模型试验的基础上，Liu G K 等［6］验证了数值算法的合理有效性，并对地下拱形结构在近区爆炸荷载下的表面荷载分布规律进行了数值研究，但没有详细分析破坏特征和规律及其与爆炸参数之间的关系。针对地下土介质中拱形结构的爆炸模型试验研究，Chen H L 等［7］着重分析了拱表面荷载分布与自由场应力之间的关系，王鹏、周健南等［8-9］通过研究拱形结构的拱顶压力分布及位移数据，分析梳理了结构的动态响应特征，证实了土体介质对爆炸波具有良好的消波作用；该研究虽描述了试验中结构的破坏特征，但未对结构的破坏等级及对应的破坏模式进行系列梳理；目前针对岩石类介质中拱形结构的动态响应及破坏特征的试验研究还相对缺乏。

在数值模拟计算结果的基础上，赵以贤等［10］采用不同的理论方法比较了拱形结构在爆炸荷载作用下的响应机制，比对了求解适用条件。朱坤芬等［11］对在核武器和常规武器条件下拱形结构端部剪力的线性及非线性响应进行了对比分析，得出了端部的响应特征。关于地下拱形结构破坏响应的数值研究方面，孙惠香等［12］基于地下结构与围岩相互作用机理的理论分析，研究了装药量、起爆位置和跨度对地下拱形结构在爆炸荷载下破坏模式的影响。夏致晰［13］、邓春梅等［14］判断了结构在应力波作用下的易损坏位移及程度。洪武等［15］发现当比例爆距在一定范围内时，2D 模型和3D模型自由场压力峰值及响应的计算结果基本一致。赵巨岩［16-17］、吴亮等［18］探究了不同装药位置和爆距下拱形工事的破坏模式，虽然发现了有效的快速简化数值计算方法，但均未对不同破坏模式对应的爆炸参数进行差异性研究和总结，没有充分分析响应参数对破坏模式和机理的影响。

针对结构参数在爆炸荷载下对破坏效应的影响，冷冰林等［19］利用仿真软件对比分析了三种材料构建的拱形结构的应力变化和压力峰值等情况，梳理了结构材料对地下拱形结构防护性能的作用；马林建等［20］分析了结构跨度、厚度对破坏机制的影响；孔大庆等［21］针对垂直爆炸下拱形结构的典型破坏形式进行了总结；孙惠香等［22］研究了结构材料和岩石介质间波阻抗的相对大小对不同跨度下拱形结构的破坏模式及特征的影响。对于结构参数对响应和破坏效果的影响，虽然已有不少的数值模拟研究成果，但数值模型的假设基础不够完善，使得已有的研究成果未能充分应用。

当前，爆炸荷载下地下工程的结构响应和破坏特征主要以数值模拟和理论分析为主，虽然也有部分的试验研究成果，但主要针对的是地下土介质中的拱形结构破坏效应；对于地下岩石类介质中的拱形结构破坏效应研究，大多成果仍体现在数值模拟方面，且主要集中在中远区爆炸荷载下的大跨度拱形结构，对于近区爆炸荷载下小跨度拱形结构抗爆性能的试验研究还相对较少。对近区爆炸荷载作用下地下拱形结构响应、破坏特征仍未见系统的梳理和总结，相应的数值计算欠缺试验对比分析，对数值计算结果的可靠性有一定影响。基于上述原因，本研究针对地下钢筋混凝土拱形结构模型在近爆作用下的抗爆性能开展了试验研究，分析了爆炸荷载下的动力响应及破坏特征，以期为地下坑道结构抗爆设计提供试验参考，也为后续钢筋混凝土拱形结构的毁伤判据建立提供试验数据。

2 试验设计与计划

2.1 构件设计

试验用的拱结构净跨度均为1200 mm，实际跨度为1500 mm，选取地下防护结构中最为常见的直墙圆拱结构进行研究，混凝土采用型号C40 商用混凝土，结构配筋采用Φ8 的HRB335 热轧带肋钢筋，箍筋采用Φ8 的HRB335 热轧带肋钢筋，结构的拱形内径600 mm，外径750 mm，侧墙内高1400 mm，外高1500 mm，受压钢筋为Φ8@140，受拉钢筋为Φ8@200，结构模型及具体截面配筋见图1 所示。试验中钢筋极限强度为566.2 MPa，屈服强度为395 MPa，伸长率29.1%，混凝土的单轴压缩强度测试值为37.2 MPa，拉伸强度为3.9 MPa，杨氏模量为32.5 GPa。

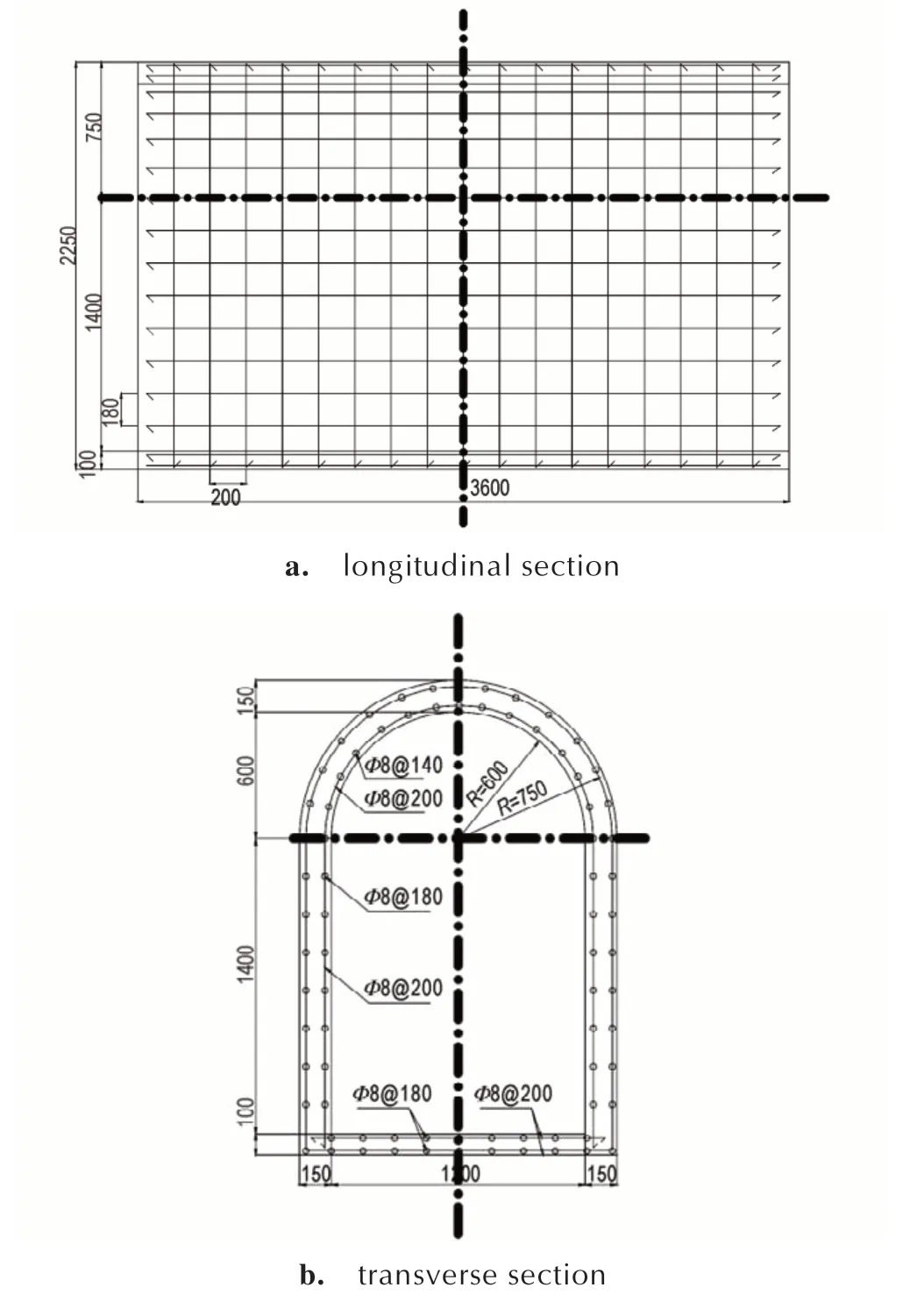
图1 拱结构截面配筋示意图Fig.1 Schematic diagram of arch sectional reinforcement

2.2 模型设计

区别于核爆条件下平面应力波的荷载形式，常规武器作用下的近区爆炸效应在地下结构上所体现荷载形式为非均布荷载，研究中需要考虑地下结构在非均布爆炸荷载下的受力性能，综合考虑地下结构的局部响应和整体响应之间的关系，加之地下岩土中爆炸效应本身的复杂性，涉及多相介质的能量传播和反射，包含爆炸冲击应力波的传播对结构带来的破坏和结构与周围介质间卸载和反射波传递作用所带来的破坏，这些都使得该方面的研究工作更加复杂。为确保研究重点，在爆炸模型系列试验研究中，做如下假定：

（1）不考虑侵彻效应部分，仅考虑侵彻到某一深度后的爆炸效应；

（2）不考虑岩体性质变化；

（3）不考虑防护层厚度变化，按封闭爆条件设计整体岩体尺寸；

试验整体边界设置及装药设计如图2 所示，通过向预留装药孔中填充炸药的形式来模拟地下爆炸。

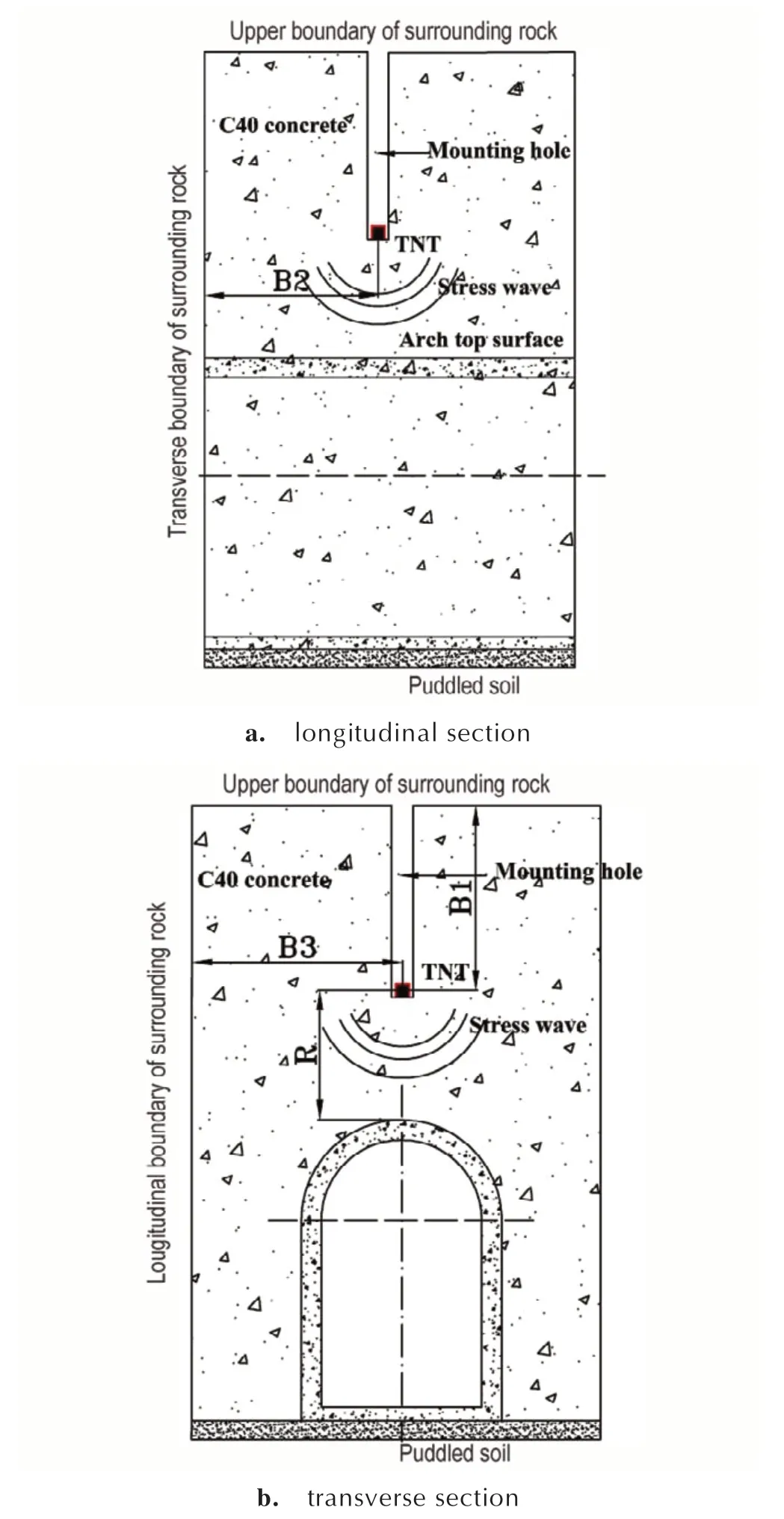
图2 顶爆下整体模型示意图Fig.2 Schematic diagram of the whole model under top explosion

实际工程中，防护工程结构处于肥沃的山体之中，没有边界效应。但试验需要利用有限的区域来模拟实际工程中无限或半无限区域，为了消除有限的边界对试验的影响，满足封闭爆条件，需要综合考虑装药量与爆距、爆炸波传播速度、爆炸波边界反射对结构响应的影响以及结构响应第一峰值出现时间等参数，拟定模拟岩体尺寸：爆心至围岩上表面边界最短距离B1、爆心距围岩横断面外边界最短距离B2、爆心距围岩轴向两侧外边界最短距离B3 应分别满足下列条件：

（1）满足封闭爆炸的条件B1、B2、B3 均大于或等于0.8ω1/3，ω 为装药量。

（2）消除上边界对结构响应影响：爆炸波到达边界后产生的反射波达到结构的时间大于结构动荷载等效 升 压 时 间tr，(2B1+ R)/Cm＞tr，又 有tr= Kttro=0.1KtR/Cm，tro= 0.1R/Cm，从而有B1＞(1+ 0.1Kt)H/2。

其中tro为结构迎爆面上爆心投影点处的压缩波升压时间，Kt为结构动荷载等效升压时间的等效系数，与爆距、结构跨度有关，按规范取值，Cm为峰值波速，根据C40强度等级的基本参数，取其峰值波速为3000 m·s-1。

（3）消除横断面和纵断面外边界对结构响应影响：爆炸波到达边界后产生的反射波达到结构的时间大于结构动荷载等效升压时间tr，2B2/Cm＞tr，即B2=B3＞0.05KtR。

（4）在现有地下结构抗爆试验的经验基础上，整体岩体横断面宽度应大于洞室跨度3～5 倍，从而有：B3＞1.5～2.5Lt（Lt= 1.2 m 为净跨度）。

结合试验设计的近区爆炸加载要求，参考空爆中近区爆炸的设计思路以及地下结构抗爆设计的相关经验，根据选定的拱形结构实际跨度，选择爆距为0.5 和1 m，分别小于和大于结构实际跨度的一半即0.75 m。

根据现行规范［23］查表取值tr和Cm进而计算对应的B1、B2、B3。计算结果见表1。

2.3 试验装置

为方便开展试验，选取最大的装药量和最大爆距下对应的边界尺寸值，统一加工制作了模具进行浇筑制作。

在试验靶场完成整体试件浇筑后，把炸药填塞至预留的装药孔施加爆炸荷载。炸药采用块状梯恩梯（TNT）炸药，由数码电雷管引爆。真实的地下结构所处的围岩环境与整体模型试验设计的有限围岩尺寸还有一定差距，为了更合理准确地模拟地下结构所处的围岩环境，在所有围岩设计工况下外围侧面加装HPB300 箍筋来更好模拟围岩边界所受的围压，并且在拱形结构洞口放置钢板，试验前对整体模型进行覆土填埋，试验模型及现场布置如图3 所示。

表1 试验计划及围岩体的设计尺寸表Table 1 Test plan and size design of surrounding rock m

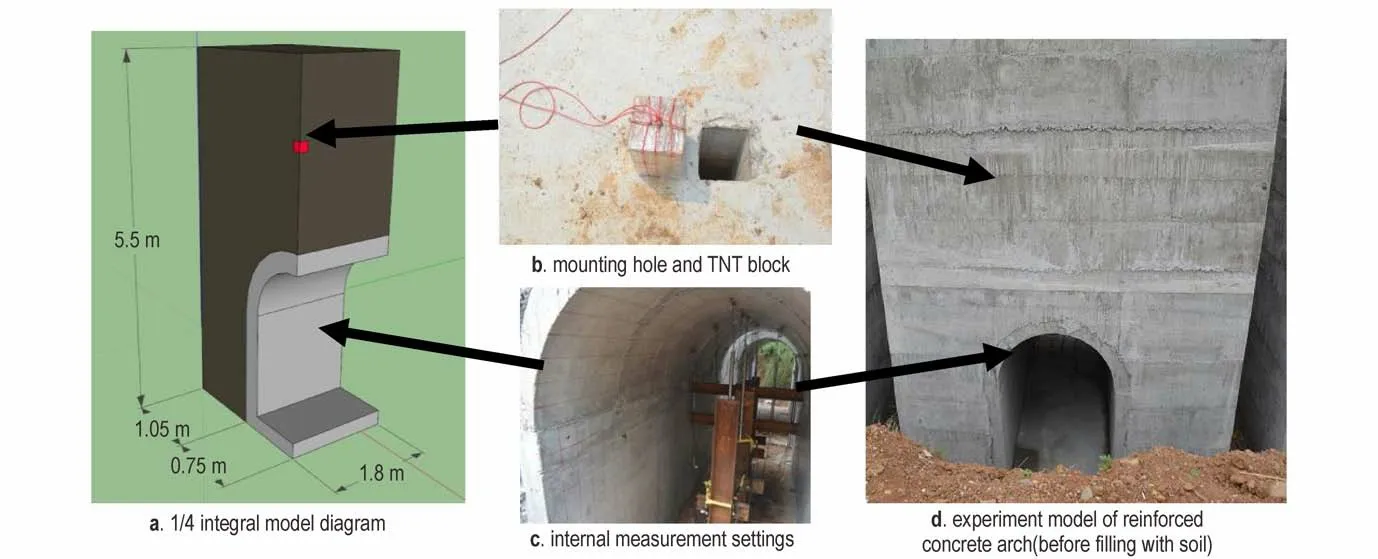
图3 顶爆下模型试验示意图Fig.3 Schematic diagram of model experiment under top explosion

3 结果及分析

为研究地下拱形结构在顶爆条件下的破坏模式及破坏等级，对比分析装药量及爆距的变化对结构破坏的影响及程度。根据McVay［24］对在爆炸载荷作用下钢筋混凝土板的层裂损伤破坏等级的定义，类似地将钢筋混凝土拱形结构的破坏分为3 个等级：（1）轻度破坏：定义为拱形结构的背爆面仅出现小裂纹，没有明显的层裂破坏；（2）中度破坏：定义为钢筋混凝土拱形结构背爆面层裂破坏，部分混凝土从钢筋混凝土拱形结构背面脱落；（3）重度破坏：定义为钢筋混凝土拱形结构崩塌破坏，背爆面中心区域混凝土显著脱落。通过试验对5个不同爆距和装药量下的钢筋混凝土拱形的破坏毁伤情况进行了梳理，给出了典型的破坏特征和破坏等级。

3.1 小爆距（R=0.5 m）对破坏效果的影响

当装药量为1 kg，爆距为0.5 m 时，试验中拱背爆面顶部出现些许细微裂纹，有微小面积混凝土层裂现象。拱弧面中心区域附近有间断的细微裂纹出现，弧面上裂纹长度最大为25 cm，纵向裂纹最长为20 cm，整个拱弧面及侧墙均无明显变形及破坏，此时钢筋混凝土拱的破坏等级为轻微破坏，破坏效果如图4所示。

当装药量为2 kg，爆距为0.5 m 时，试验中的破坏程度有所增强，体现为拱顶中心区域的弧向部分钢筋出现裸露并向下隆起现象，外露钢筋根数为8 个，最大隆起高度为2.2cm，裸露钢筋周围混凝土层出现分散的小面积剥落，长度最大为57 cm，最大剥落块区域长度为2 cm、宽为1.5 cm、深度为2 cm。并且拱形背爆面出现了纵向钢筋裸露，伴随着混凝土脱落出现纵向明显的贯穿破坏区域的裂纹，最大长度约为80 cm。拱侧墙和拱脚均未出现裂纹和混凝土层裂。总之，虽然与1 kg 装药和0.5 m 爆距下的破坏效果相比拱弧面上开始出现了纵向的层裂且混凝土脱落现象层裂破坏更为明显，但破坏特征仍为局部钢筋隆起和混凝土层剥落，拱整体无明显变形，拱侧墙和拱脚无破坏，且拱顶钢筋隆起高度、剥落块面积相对较小，所以此时钢筋混凝土拱的破坏等级为中度破坏，破坏效果如图5所示。

图4 钢筋混凝土拱D1 的破坏效果（R=0.5 m，ω=1 kg）Fig.4 Damage effect of reinforced concrete arch D1（R=0.5 m，ω=1 kg）

图5 钢筋混凝土拱D2 的破坏效果（R=0.5 m，ω=2 kg）Fig.5 Damage effect of reinforced concrete arch D2（R=0.5 m，ω=2 kg）

当装药量为6.4 kg，爆距为0.5 m 时，与D1、D2 的破坏效果相比拱形顶部中心处破坏增强显著，具体破坏特征体现为在角度左侧45°至右侧45°，在角度35°～45°范围内钢筋严重弯剪变形，一侧严重变形4 个，一侧5 个，外露钢筋尺寸沿弧向最大长度为25 cm，且伴随混凝土脱落，最大混凝土脱落区域为长度20 cm、宽度16 cm、深度5 cm，关于中心点对称出现了纵向长度约145 cm、宽度为23 cm 的局部严重崩塌破坏区域，除在中心区域出现由弧面延伸至侧墙的裂纹，最长为75 cm，拱脚及侧墙无明显破坏。总之，随着装药量的增加，拱结构的破坏由混凝土的层裂和钢筋的隆起转变为钢筋的弯剪变形及混凝土的崩塌脱落，虽然拱侧墙和拱脚无显著破坏，但拱弧面上的钢筋变形显著及混凝土崩塌严重，拱形结构整体出现了较为显著局部的破坏，此时钢筋混凝土拱的破坏等级为重度破坏，破坏效果如图6 所示。

图6 钢筋混凝土拱D3 的破坏效果（R=0.5 m，ω=6.4 kg）Fig.6 Damage effect of reinforced concrete arch D3（R=0.5 m，ω=6.4 kg）

3.2 大爆距（R=1 m）对破坏效果的影响

当装药量为6.4 kg，爆距为1 m 时，与D3 的相比破坏效果明显降低，没有了混凝土的崩塌和钢筋的弯剪变形，具体体现为中心处拱形弧向混凝土脱落、钢筋外露，钢筋外露根数3 个，钢筋基本无隆起，裸露钢筋周围混凝土层出现分散的小面积剥落，长度最大为20 cm。弧形裂纹密布，大多都延伸至拱脚，裂纹数由中心至两端逐渐减少，中心处的裂纹延伸至侧墙下半部。拱顶出现纵向的明显裂纹，长度最长约为40cm。与D2 的破坏效果相比，不同的为拱弧面的裂纹裂隙有一定程度的延展，相同的是钢筋基本无隆起、混凝土的剥落程度且剥落区域面积也相对较小，总之，拱整体无明显变形，侧墙和拱脚无明显破坏，此时钢筋混凝土拱的破坏等级为轻微破坏，破坏效果如图7 所示。

图7 钢筋混凝土拱D4 破坏效果（R=1 m，ω=6.4 kg）Fig.7 Damage effect of reinforced concrete arch D4（R=1 m，ω=6.4 kg）

当装药量为8 kg，爆距为1 m 时，与D4 相比破坏程度略微增大，具体体现为拱形中心处环向钢筋外露明显，伴随混凝土脱落，拱顶部纵向贯穿破坏区域的裂纹，长度最长约为60 cm。中心处附近钢筋外露根数5 个，最长外露长度为44 cm，隆起不明显，中心处出现延伸穿过拱脚直至侧墙底部的裂纹。虽然与D4 的破坏相比环向钢筋外露的长度及根数增加和裂纹向侧墙的延伸，但破坏效果仍表现为局部的钢筋外露、轻微隆起和些许混凝土层剥落，拱整体无明显变形，拱侧墙和拱脚无破坏，且拱顶钢筋外露长度、剥落区域面积较小，所以此时钢筋混凝土拱的破坏等级为轻微破坏，破坏效果见图8。

3.3 破坏模式分析

图8 钢筋混凝土拱D5 的破坏效果（R=1 m，ω=8 kg）Fig.8 Damage effect of reinforced concrete arch D5（R=1 m，ω=8 kg）

爆炸产生的球面波向外传播，形成冲击波阵面，开始在岩石介质中传播，当传播至围岩与拱形结构接触面时，会产生发射和透射现象，透射过界面的应力波在拱形结构的自由临空面再次反射后，拱形结构表面的混凝土开始出现层裂崩塌，随着破坏的继续发展，拱形结构会出现不同的破坏模式。

当爆距较大（R=1 m）时，钢筋混凝土拱的破坏主要体现为混凝土的剥落及钢筋的外露及变形。TNT装药量为6.4 kg 时，钢筋混凝土拱背爆面的层裂剥落现象并不明显；TNT 装药量为8 kg 时，钢筋混凝土拱背爆面的层裂剥落明显增加，且破坏范围也有明显的扩大，中心区域弧向最大脱落直径为44 cm，最大脱落深度为4 cm，弧向及纵向的层裂分布均较明显，且裂纹延伸范围扩展至拱脚并向侧墙有所延伸。此时钢筋混凝土拱的主要破坏模式为整体弯曲局部崩塌破坏。

当爆距较小（R=0.5 m）时，钢筋混凝土拱形的结构的破坏模式以顶部区域弯曲破坏为主，随着装药量的增加，钢筋混凝土拱开始出现中部区域的层裂冲切破坏，并开始呈现崩塌贯穿破坏的趋势。当TNT 装药量为1 kg 时，钢筋混凝土拱背爆面仅出现细微裂纹和少许的层裂破坏，范围很小；当TNT 装药量为2 kg 时，钢筋混凝土拱背爆面出现了显著的层裂破坏并开始出现纵向的层裂破坏，钢筋外露明显且范围较大；当TNT 装药量为6.4 kg 时，钢筋混凝土拱出现显著的崩塌破坏，在弧向上40°附近出现显著混凝土的崩塌脱落以及明显的钢筋弯曲变形，纵向上出现关于中心对称的两个混凝土崩塌断裂带，整体上破坏呈现漏斗状，中心处位移变化幅度最大，但在破坏区域的边界处，破坏程度最大最集中，此时的背爆面的弧向层裂直径约为750 mm，纵向层裂直径约为1200 mm，拱顶对应的最大位移为51.2 mm，此时钢筋混凝土拱的破坏呈现处中弧向40°附近处的局部弯剪破坏和整体拱形的弯曲破坏。

综上，当爆距较近或装药量较大时，TNT 药块在短时间内释放巨大能量，引起围岩介质的瞬时响应，在爆炸点附近及拱形结构表面产生应力的跃升，造成结构的破坏。当爆源距离钢筋混凝土拱形结构较近时，因拱形结构的结构特性及受力特征，会在拱顶附近产生峰值较高、持续时间较短的脉冲荷载，且在拱顶处附近产生应力集中现象，造成结构的层裂及震塌破坏，当承受的爆炸荷载超过结构的破坏阈值时，拱形结构会发生整体震塌贯穿破坏。

3.4 破坏等级划分

在试验过程中对钢筋混凝土拱顶部的竖向位移进行了测量，结果见表2。由表2 可看出，随着装药量的增加，顶部位移逐渐增加，挠跨比a（位移峰值与实际跨度之比）逐渐增加，背爆面弧向、纵向的层裂直径也逐渐增加；随着比例距离的减小，钢筋混凝土拱的破坏等级也逐渐增加。

为判别钢筋混凝土拱的破坏等级，在试验基础上对钢筋混凝土拱的破坏等级进行划分，划分依据为挠跨比a，a＜3%时为轻微破坏；破坏形式为背爆面的出现少量裂纹；3%≤a＜8%时为中度破坏；破坏形式为拱顶部出现弯曲变形，弧向、纵向的混凝土层裂及弧向钢筋变形外露；a≥8%时为重度破坏；拱的整体变形较大，崩塌层裂显著，钢筋严重变形。

通过试验发现，在近区爆炸荷载作用下，地下钢筋混凝土拱结构的破坏不仅与比例距离Z 密切相关，还与爆距与结构跨度的长度比相关。在相同爆距下，随着比例距离的增大，中心点的位移明显减小，见图9，对应的破坏程度也逐渐减弱；同一比例距离（Z=0.5 m·kg-1/3）下，爆距为1 m 时的中心最大位移比爆距为0.5 m 时增大了近13 倍，见图10，且环向层裂直径增加了56%，纵向层裂直径增加了200%，见表3，虽然破坏等级都为轻微破坏，但破坏的程度随着爆距的增加有了明显的增强。在同一装药量（ω=6.4 kg）条件下，Z≥0.5 m·kg-1/3时，拱轻微破坏，0.5 m·kg-1/3≥Z＞0.269 m·kg-1/3时，拱中度破坏；Z≤0.269 m·kg-1/3时，拱重度破坏，见表2。

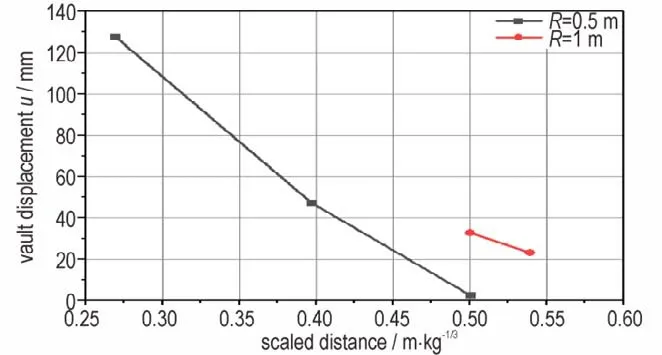
图9 中心点位移随比例距离变化关系Fig.9 The relationship between center point displacement and scaled distance

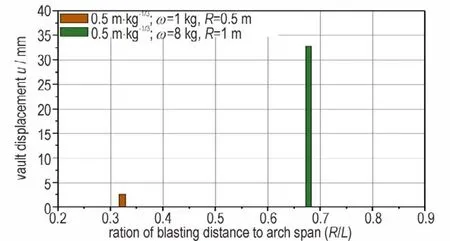
图10 中心点位移随爆距与拱跨度之比变化关系Fig.10 The relationship between center point displacement and the ratio of blasting distance to arch span

表2 顶爆下钢筋混凝拱试验结果Table 2 Test results of reinforced concrete arch under top explosion

4 结论

通过对钢筋混凝土拱的爆炸模型试验，研究了封闭爆炸荷载作用下钢筋混凝土拱的主要破坏模式及响应特征，在此基础上，分析了位移响应与装药量及爆距的关系，并结合对应的破坏模式，初步提出了以挠跨比为依据的破坏等级划分方法。其主要结论如下：

（1）针对同一爆距作用下，且爆距较小时（小于拱形跨度），随着装药量的增加，拱的破坏程度逐渐增加，破坏模式由背爆面中心混凝土层剥落、钢筋外露，逐渐增加至钢筋隆起，最终拱顶中心处混凝土显著塌落、钢筋严重弯曲变形。针对同一爆距作用下，且爆距较大时（大于拱形跨度），随着装药量的增加，拱的破坏程度虽然也有所增加，但相较于较小爆距下的破坏程度增加不大，主要破坏特征体现在破坏范围有所增大，裂纹裂隙延伸至侧墙底部。

（2）拱的破坏程度不仅与比例距离相关，还受爆距与结构跨度之比的影响，在同一比例距离下，爆距越大，拱的破坏程度越显著。

（3）拱的挠跨比a＜3%时为轻微破坏，破坏模式主要是拱背爆面出现细微裂纹，中心处有少许混凝土层剥落；3%≤a＜8%时为中度破坏，破坏模式为拱顶部出现弯曲变形，混凝土层裂明显及钢筋些许变形；8%≤a时为重度破坏，拱顶部显著变形，弧面拱腰处混凝土崩塌破坏及钢筋弯曲变形显著，局部破坏显著；试验中虽没能做出严重的破坏模式，但基于上述各破坏模式的梳理并结合钢筋混凝土板类构件的破坏特征，对严重破坏程度下的破坏模式作出了预测，预测破坏模式为中心处崩塌贯穿，弧面拱腰附近钢筋严重变形直至断裂，整体变形显著，在起爆点与结构投影位置局部区域内完全丧失防护承载能力。通过对试验数据的分析梳理研究了地下拱结构的破坏特征与爆炸参量之间的关系，这些位移响应峰值和破坏模式可以作为结构抗爆设计的依据，为今后的结构破坏评估分析提供试验支撑。