时变时滞随机马尔科夫跳变系统非脆弱H动态输出反馈控制器设计
2021-03-30林玉倩尹月霞庄光明
林玉倩,尹月霞,孙 梦,王 馨,庄光明
(聊城大学 数学科学学院,山东 聊城 252059)
0 引言
马尔科夫跳变系统作为一种混合随机系统,在电力系统、BM/C3、太阳能热系统等领域具有很强的实际应用价值,在过去几十年里得到了许多非常重要的研究结果[1-6]。马尔科夫跳变系统与时间演化和事件机制有关,且对于突发现象的建模,它可用于表示随机故障和环境的突发性变化,对模块进行更新,改变子系统之间的互联性等[7-9]。众所周知,马尔可夫过程决定了不同模式的跳变和突变,而在跳变或者转换过程中概率测度则决定了马尔科夫跳变系统的行为[10-13]。
由于随机系统在机械系统、经济学、人类操作系统等领域的广泛应用,近几十年来受到了广泛的关注。在实际应用中,这些系统往往受到噪声的破坏,如布朗运动,且许多研究问题都与H反馈控制和滤波有关[14]。在文献[15]中,给出了一种简洁的连续随机系统的H控制器,并用耦合非线性矩阵不等式表示。文献[16]研究了参数不确定性和时滞随机系统的H控制,其中假设所有状态变量对状态反馈控制都可行。近年来,随机马尔科夫跳变系统受到了广泛的关注,并且出现了各种有意义的随机马尔科夫跳变系统的研究结果[17-21]。
在许多情况下,时滞往往是许多动态系统性能差和不稳定的根源[22]。在此基础上,时滞系统的稳定性问题,特别是时变时滞系统的稳定性问题在过去几十年中受到了广泛关注[23-27]。文献[28]研究了对于时变时滞系统的H状态反馈控制问题,并采用了修正的代数Riccati方程和线性矩阵不等式方法。
在大多数相关文献中,假设动态系统的状态是完全可测的,并且状态反馈控制可以轻松实现[29]。然而,在实践中,不可避免的是状态信息并不总是完全可测的。针对这种情况,控制器的分析和设计主要涉及两种方法,第一种方法是设计一个基于观测器的控制器,通过观测器可以重构动态系统的状态[30,31]。第二种方法是设计一个动态输出反馈控制器,利用动态系统的测量输出信号实现反馈控制[32,33]。在实际控制应用与实施中,当系统状态不可用时,由于完整的状态信息难以获取而系统输出信号易于获取,输出反馈控制策略就显得非常重要。
另一方面,非脆弱性现象在现实系统中是不可避免的,非脆弱控制策略的研究不仅集中在理论分析上,而且在实际应用中也得到了广泛关注[34-37]。非脆弱控制是指设计一个反馈控制器,使控制器不受由数值舍入误差、固有误差或执行器退化等引起的增益的不确定性影响。据作者有限的知识所知,具有时变时滞的随机马尔科夫跳变系统的非脆弱鲁棒H动态输出反馈控制的问题仍然是开放并充满挑战的。
受上述问题的启发,本文将研究具有时变时滞随机马尔科夫跳变系统非脆弱H动态输出反馈控制器的问题。主要目标是研究具有更快收敛速度和更好准确性的时变时滞随机马尔科夫跳变系统鲁棒指数均方稳定问题;设计的动态输出反馈控制器能确保鲁棒指数均方稳定和闭环随机马尔科夫跳变系统的H性能指标; 设计的动态输出反馈控制器具有非脆弱的特性,并保证闭环随机马尔科夫跳变系统的鲁棒性。
1 问题描述
本文研究的具有时变时滞的随机马尔科夫跳变系统
(1)
其中x(t)∈Rn是系统的状态,φ(t)是初始状态,z(t)∈Rq是估计输出,u(t)∈Rm是控制输入,v(t)∈Rp是属于L2[0,+)的扰动输入,y(t)∈Rr是测量输出,ω(t)是概率空间(Ω,F,P)上的Wiener过程。{rt}是右连续的马尔科夫过程且独立于ω(t),{rt}在有限集合S={1,2,…,N}中取值。πij是马尔科夫过程的转移率[4]。τ1(t,rt)和τ2(t,rt)是系统状态中的时变时滞,对∀rt=i∈S,满足
(2)
其中h1,h2,u1,u2是实常数标量,h=max{h1,h2}.A(rt),Ad(rt),B1(rt),B2(rt),B3(rt),C(rt),Cd(rt),D1(rt),D2(rt),E(rt),Ed(rt),Gd(rt)是已知的常数矩阵。
在本文中,将考虑如下全阶非脆弱动态输出反馈控制器
(3)
其中ζ(t)∈Rm是控制器状态,AΔK(rt)=AK(rt)+ΔAK(rt),BΔK(rt)=BK(rt)+ΔBK(rt),CΔK(rt)=CK(rt)+ΔCK(rt),AK(rt),BK(rt),CK(rt)是动态输出反馈控制器的未知参数,且
(4)
ΔCK(rt)=L2(rt)F(rt)Ec(rt),
(5)
其中L1(rt)∈Rn×r,L2(rt)∈Rm×r,Ea(rt)∈Rr×n,Eb(rt)∈Rr×l,Ec(rt)∈Rr×n,是已知的实常数矩阵。将式(4)代入式(1)得闭环系统
(6)
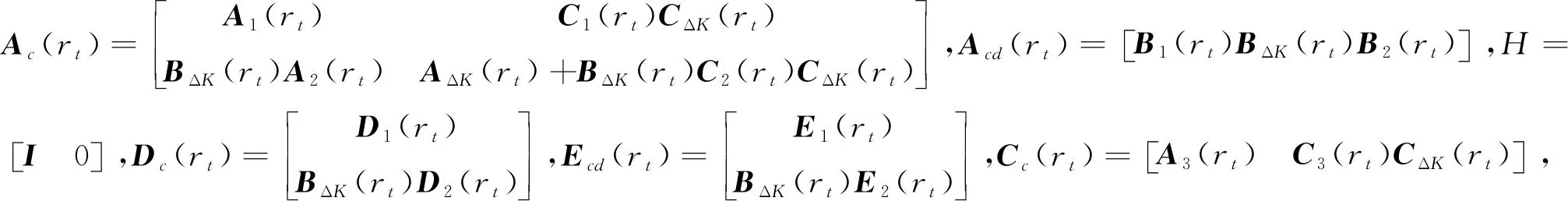
定义1[9]对于未加控制输入u(t)的随机马尔科夫跳变系统(6),如果∃d>0,c>0使得
(7)
成立,其中φ是r0的初始状态,则称未加控制输入u(t)的随机马尔科夫跳变系统(6)是鲁棒指数均方稳定的。
定义2[11]对于随机马尔科夫跳变系统(6),若对于标量α>0,γ>0和任一非零v(t)∈L2[0,+) 有
(8)
成立,其中φ是r0的初始状态,则称随机马尔科夫跳变系统(6)满足H性能指标γ。
2 主要结果
定理1 未加控制输入u(t)的随机马尔科夫跳变系统(6)是鲁棒指数均方稳定并满足H性能指标γ,如果对∀rt=i∈S, ∃ε1>0,ε2>0和矩阵Pi>0,Q1>0,Q2>0使得以下的线性矩阵不等式成立
(9)

证明首先,考虑当v(t)=0时,系统(6)为
dη(t)=[Ac(rt)η(t)+Acd(rt)Hη(t-τ1(t,rt))]dt+Ecd(rt)Hη(t-τ2(t,rt))dω(t),
(10)
让η(t)=η(t+θ),θ∈[-h,0],且取L-K函数
V(ηt,rt)=V1(ηt,rt)+V2(ηt,rt)+V3(ηt,rt)+V4(ηt,rt)+V5(ηt,rt),
(11)

令A为随机过程{ηt,rt}的弱无穷小微分算子,根据It公式,可得
(12)
(13)
(14)

(15)

(16)
因此,由(2)和(11)-(16)可推出
(17)
其中x(t-τ1i(t))=Hη(t-τ1i(t),x(t-τ2i(t))=Hη(t-τ2i(t))。且对于j≠i,πii≤0马尔科夫转移率πij≥0,并令η=max{|πii|,i∈S},有

(18)
则有
(19)
其中
因此,通过Dynkin公式,得到具有时变时滞的随机马尔科夫跳变系统(6)是随机稳定的。为证具有时变时滞的随机马尔科夫跳变系统(6)是鲁棒指数均方稳定的,我们指出
AV(ηt,i)≤-a|η(t)|2,
(20)
其中a=λmin(-Vi)>0。则
dV(ηt,i)≤-a|η(t)|2dt+2η(t)TPiEcdiHη(t-τ2i(t))dω(t)。
(21)
令β>0使
βb-a+2βbheβh(1+ηh)=0,
(22)
其中b=max{λmax(Pi),λmax(HTQ1H),λmax(HTQ2H)}。
考虑到
(23)
(24)

其次,对于初始条件v(t)∈L2[0,)有
dV(ηt,i)=A1V(ηt,i)dt+2η(t)TPiEcdi(t)Hη(t-τ2i(t))dω(t),
(25)
其中V(ηt,t)在(11)中已给出,且
(26)
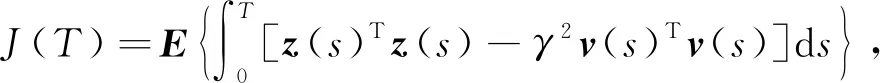
则有
(27)
其中
则对T>0,有J(T)<0,故系统(6)在零初始条件以及ω(t)≠0时满足H性能指标γ。定理得证。
定理2 对于标量γ>0和给定的标量εl>0,l=1,2,…,7,存在一个非脆弱动态输出反馈控制器(3)使得闭环系统(6)满足鲁棒指数均方稳定和H性能指标,如果对所有的rt=i∈S,存在矩阵Pi>0,R>0,Q1>0,Xi>0,Yi>0,Q2>0,Yi,Φi和Ψi使得以下的线性矩阵不等式成立
(28)
其中
+(1+ηh)HT(Q1+Q2)H,
此时,非脆弱动态输出反馈控制器(4)的参数可表示为
(29)
其中Si和Wi是可逆的且满足
(30)
证明注意,总存在可逆矩阵Si和Wi使得(30)成立,并且我们从(28)可得
(31)
(32)
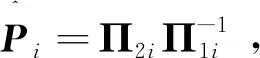
(33)

则(28)可重写为
(34)
其中
对于给定的标量εl>0,l=1,2,…7,且矩阵Q1>0,Q2>0,由(34)可以发现
(35)
其中



通过Schur补满足定理1的公式(9)。此时期望得到的非脆弱输出反馈控制器(3)可由(29)实现。定理得证。
注释1定理2给出了利用非脆弱动态输出反馈控制器解决随机马尔科夫跳变系统鲁棒H控制问题的充分条件。其中当εl>0,l=1,2,…7,是给定的,Yi,Φi,Ψi,Q1>0,Xi>0,Yi>0,Q2>0是未知的,(28)是一个线性矩阵不等式,这就定义了一个凸解集,因此(28)可以通过全局收敛的凸规划工具求解[14]。对于(28)中的Q2,Q1是以非线性形式出现的,而这种情况在处理具有时滞的输出反馈控制问题时经常会遇到的情况[14]。但在状态反馈控制器的设计中,通常可以通过求解一个严格的线性矩阵不等式来得到理想的控制器,且须要确定的参数要少得多。因此,输出反馈控制器的设计要比状态反馈情况复杂得多。
3 仿真例子





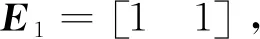
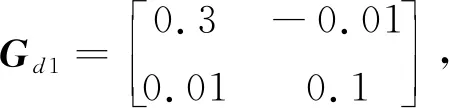
当u1=0.06,u2=0.7,h=4.5时,解线性矩阵不等式(28)和方程(30),可以获得H性能指标γ=5.8633和非脆弱动态输出反馈控制器(4)的参数如
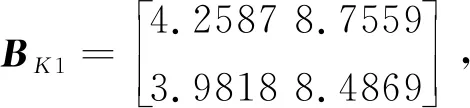


图1给出了基于马尔科夫跳变转移率矩阵Π的动态输出反馈控制器闭环随机马尔科夫跳变系统状态x(t),图2展示了基于马尔科夫跳变转移率矩阵Π的非脆弱动态输出反馈控制器的状态,图3描绘了基于马尔科夫跳变转移率矩阵Π的增广系统状态η(t),图4绘制了基于马尔科夫跳变转移率矩阵Π的估计输出状态z(t)。

图1 基于跳变转移率矩阵Π的动态输出反馈控制器闭环随机跳变系统状态x(t)
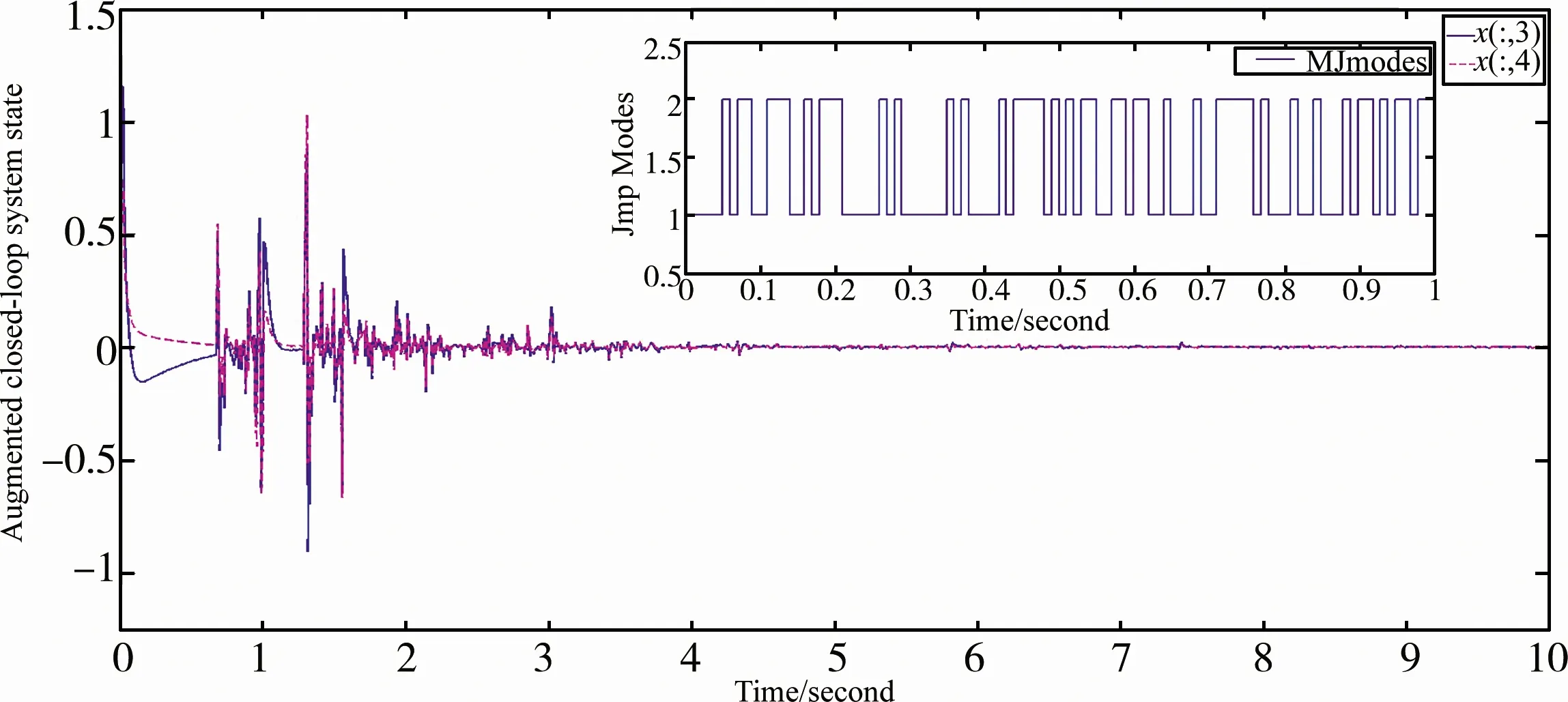
图2 基于马尔科夫跳变转移率矩阵Π的非脆弱动态输出反馈控制器状态

图3 基于马尔科夫跳变转移率矩阵Π的增广系统状态η(t)

图4 基于马尔科夫跳变转移率矩阵Π的估计输出状态z(t)
4 结论
本文具体研究了具有时变时滞的随机马尔科夫跳变系统的非脆弱H动态输出反馈控制器问题。目的是设计一个全阶非脆弱动态输出反馈控制器以证明闭环随机马尔科夫跳变系统的指数均方稳定和H性能指标。并且用线性矩阵不等式对非脆弱动态输出反馈控制器的存在条件进行了改进。最后通过实际例子-工业非等温连续搅拌釜反应器,验证了本文方法的有效性和正确性。在未来的工作中,将重点讨论在理论上时变时滞的最大值问题,并引入自由权矩阵技术来获得具有一般的导数约束时滞相关的充分条件。
