樽海鞘群算法在电力系统最优潮流计算中的应用

张 凡，王 雷，赵 娟，吴 磊

(中国电力工程顾问集团西北电力设计院有限公司，陕西省 西安市 710000)

0 引言

最优潮流计算与电力系统的稳定、经济运行密切相关，自20世纪60年代提出最优潮流的概念以来[1]，大量学者相继提出了各种优化技术来求解电力系统的最优潮流问题[2-10]。

樽海鞘群算法(salp swarm algorithm, SSA)是澳大利亚学者Seyedali Mirjalili于2017年提出的一种新型群智能算法[11]。目前已在焊接梁问题[12]、飞行器再入轨迹优化[13]、辐射源定位[14]、光伏系统最大功率追踪[15]、STATCOM 模型参数解耦辨识[16]、需求响应补贴定价[17]等领域得到了广泛的应用。

然而，目前对樽海鞘群算法在电力系统最优潮流方面应用的研究仍较少。文献[18]采用樽海鞘群算法求解含风电电力系统的经济调度问题，并指出樽海鞘群算法相比共生生物搜索算法可求得更低的发电成本。文献[19]进一步研究了通过樽海鞘群算法求解含随机风电的多区域经济调度问题，通过与改进和声搜索算法、飞蛾扑火算法、人工蜂群算法、花朵授粉算法等其他算法进行对比，验证了樽海鞘群算法的优越性。文献[20]研究了多目标樽海鞘群算法(multi-objective salp swarm algorithm, MSSA)在含高比例风光新能源电网中的应用，并提出与快速非支配解排序遗传算法、强度帕累托进化算法相比，多目标樽海鞘群算法获得的帕累托前沿分布更广、更均匀。

在原始的樽海鞘群算法中，跟随者是按照领导者的位置依次更新其位置的，而领导者取为种群中适应度最优的个体[11]，目前包括文献[18-20]在内的大多数文献均采用这种设置。但这种领导者的选取方式在一定程度上存在降低种群多样性、使算法易于陷入局部最优的可能。文献[12]和文献[14]就提出，可以采用将种群中的一半个体取为领导者的更新策略，但并未对比不同的领导者选取方式对算法优化效果的影响。

本文将樽海鞘群算法用于求解IEEE 30节点系统及IEEE 118节点系统的最优潮流问题，以系统网损、电压偏移、发电成本和电压稳定度为目标，研究了将领导者取种群中最优个体或取种群中适应度较好的前10%～50%的个体对算法求解单目标和多目标最优潮流问题的优化效果的影响。结果表明将樽海鞘群算法中的领导者比例取为种群中适应度较好的前20%到40%时，较算法原有的将领导者取种群中最优个体的更新策略，可以取得相对更好的最优潮流求解结果。

1 数学模型

1.1 目标函数

1) 系统网损。

电力系统网损目标函数为

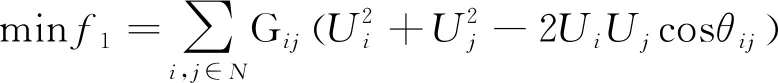
(1)

式中：N为节点总数；Gij为节点i和节点j之间的线路电导；Ui和Uj分别为节点i、j处的电压；θij为节点i、j之间的相角差。

2) 电压偏移。

电压偏移目标函数为

(2)

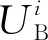
3) 发电成本。

发电机的发电(燃料)成本目标函数为

(3)

式中：costi为发电机i的发电成本；ai、bi和ci为发电机i的成本系数；NG为发电机节点数；PG为发电机有功出力。

4) 电压稳定度。

本文采用文献[21]中的雅克比矩阵最小奇异值指标来衡量电力系统的电压稳定度。将收敛潮流的雅克比矩阵J∈Rm×m进行奇异值分解得：

J=VΣUT

(4)

式中：V和U分别为矩阵J的左右奇异向量构成的正交矩阵；Σ为奇异值组成的对角矩阵。设奇异值为δi，i、ui分别为V、U中δi所对应的列向量，则式(4)可写为

(5)

令δmin为最小奇异值，当δmin≠0时，有：

(6)

式中：ΔP、ΔQ为节点注入功率向量的偏差量；Δθ、ΔU为节点相角和电压的偏差量。

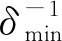
电压稳定度目标函数为

(7)

使用罚函数项处理状态变量的不等式约束，将需要优化的目标值J表示如下：

(8)

其中：

式中：fk代表原求解目标；ηU和ηQ分别为负荷节点电压和发电机无功出力越限的罚系数；ΔUi和ΔQj分别为负荷节点电压和发电机无功出力越限的惩罚项。

1.2 等式约束

等式约束包括：

(11)

式中：Pi、Qi分别为节点i、j注入的有功和无功功率；Bij为节点i、j之间的线路电纳。

1.3 不等式约束

控制变量的不等式约束包括：

(12)

式中：UG、T、QC分别为发电机机端电压、变压器变比、并联电容器补偿容量；上标max、min表示变量的上下限。

状态变量的不等式约束包括:

(13)

式中：UB、QG分别为负荷节点的电压和发电机的无功出力。

2 樽海鞘群算法

2.1 单目标樽海鞘群算法

樽海鞘属于海樽科，是一种类似水母的海洋生物，在深海中，樽海鞘通常会形成一个称为樽海鞘链的群体，有关研究认为该行为有助于其快速协调运动和觅食。樽海鞘群算法将种群分为领导者和追随者两部分，领导者处于长链的前端以引导整个种群，追随者则追随其运动。

在原始的樽海鞘群算法中，以算法的寻优目标作为食物源F，领导者的位置更新公式为

(14)

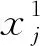
(15)

式中：l为当前迭代次数；L为最大迭代次数。

追随者的位置更新公式为

(16)

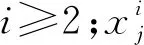
考虑到将领导者取为种群中适应度最优的个体时，可能会降低种群多样性，使算法易于陷入局部最优。本文尝试选取种群中适应度较优的前Nmaxr个个体为领导者，其中Nmax为种群规模，r为选取的领导者比例。

2.2 多目标樽海鞘群算法

由于多目标优化问题求解的是一个帕累托最优解集，需要对原樽海鞘群算法进行一些调整以得到MSSA。假设希望获得的非支配解的个数为M，MSSA的基本思路如下文所述。

1) 设置一个存储池来存储算法求解得到的非支配解集。

2) 每当迭代更新中获得的新解支配了存储池中的一个或几个旧解时，将新解装入存储池，并抛弃被其所支配的旧解。当新解与存储池中的旧解构成非支配关系时，将新解装入存储池。当新解被存储池中的至少一个旧解支配时，抛弃新解。

3) 根据非支配解i的邻解的密集程度，为其分配一个等级ranki，等级越高代表其周围邻解越多，说明该解附近的解越密集。当存储池中的非支配解总数超过M时，抛弃等级较高即邻解较密集的解，确保存储池中解的总数为M，并使整个帕累托解集分布的尽量广泛和均匀。

4) 由于存储池中的个体均为非支配解，实际上已不存在绝对“最优”的个体，根据各解的等级使用轮盘赌选择的方式确定下一代领导者所要追寻的食物源个体。

为定量描述2组解集的优劣程度。本文使用C指标[22]来做进一步分析。C指标可用于描述2个解集之间的支配关系，对于2个解集Q1和Q2，其计算公式为

(17)

式中：C(Q1,Q2)为Q1关于Q2的C指标，可衡量Q2中有多大比例的解被Q1中的解支配，例如C(Q1,Q2)=0.6表示Q2中有60%的解被Q1中的解支配。

3 算例分析

算例分析中以10%为步长，将樽海鞘群算法的领导者比例取在10%到50%之间，并与原始樽海鞘群算法将领导者取种群最优个体的策略进行对比，研究将算法中的领导者比例取为不同值对其求解最优潮流问题效果的影响。最优潮流计算在配有Core i7-8565U、1.8 GHz，8 GB RAM的PC机上进行。

3.1 IEEE 30节点系统(单目标优化)

以往不同文献中IEEE 30节点系统参数略有差别，本文采用文献[3]中的相应参数。对于控制变量、状态变量的约束和罚因子的取值见文献[23]。为贴近实际生产运行，将变压器变比由[0.9,1.1]之间连续调节改为[0.9,1.1]之间分16档进行分档调节，另外，在求解电压稳定度指标时将负荷节点的电压约束松弛为[0.95,1.1]，其他不变。该算例初始惩罚项为29.002。算法种群规模设置为40，迭代次数设置为500。各种领导者比例下独立运行10次并统计计算结果。

3.1.1 系统网损

IEEE 30节点系统的初始网损为5.860 MW。不同的领导者比例下，樽海鞘群算法对IEEE 30节点系统的网损目标值优化结果见表1，不同领导者比例求网损目标值的箱线图如图1所示。

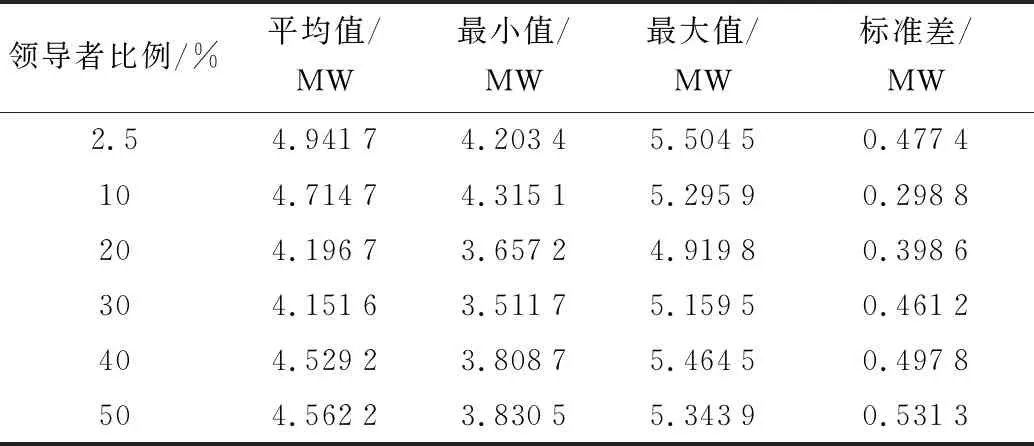
表1 不同领导者比例下IEEE 30节点系统网损目标值优化结果

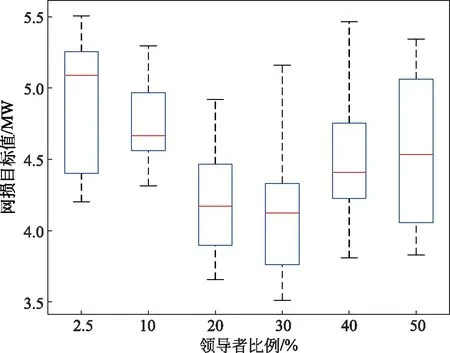
图1 不同领导者比例下樽海鞘群算法求解IEEE 30节点系统网损目标值的箱线图

3.1.2 电压偏移

IEEE 30节点系统的初始电压偏移为1.170。不同的领导者比例下，樽海鞘群算法对IEEE 30节点系统的电压偏移目标值优化结果见表2，不同领导者比例求电压偏移目标值的箱线图如图2所示。

3.1.3 发电成本

IEEE 30节点系统的初始发电成本为902.053 8 $/h。不同的领导者比例下，樽海鞘群算法对IEEE 30节点系统的发电成本目标值优化结果见表3，不同领导者比例求发电成本目标值的箱线图如图3所示。

表2 不同领导者比例下IEEE 30节点系统电压偏移目标值优化结果

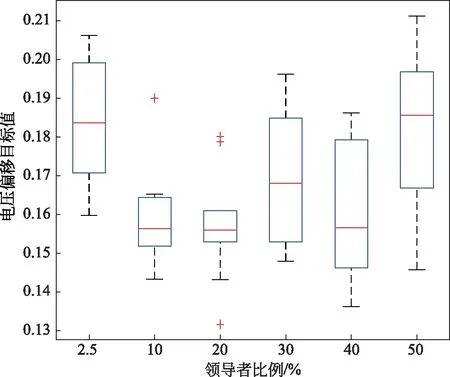
图2 不同领导者比例下樽海鞘群算法求解IEEE 30节点系统电压偏移目标值的箱线图

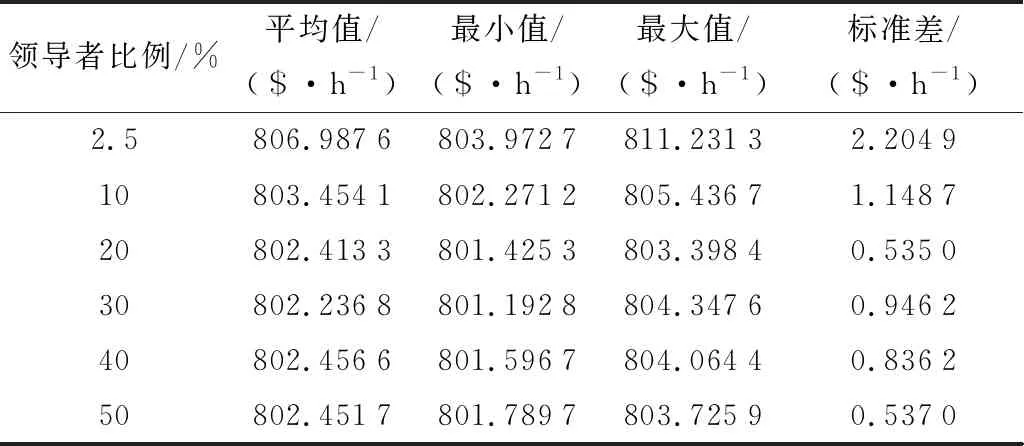
表3 不同领导者比例下IEEE 30节点系统发电成本目标值优化结果

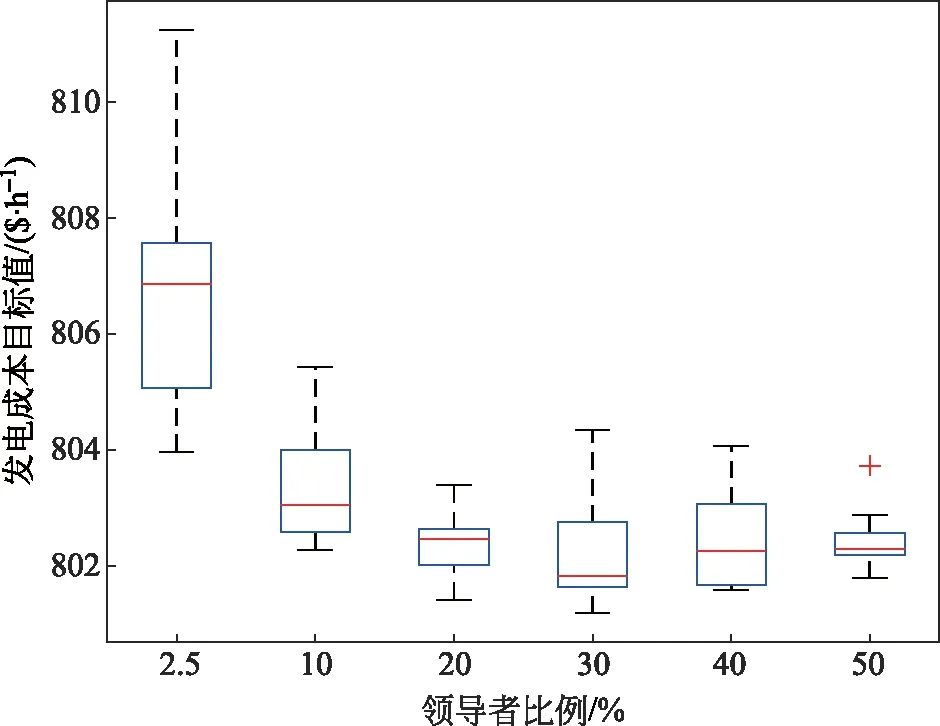
图3 不同领导者比例下樽海鞘群算法求解IEEE 30节点系统发电成本目标值的箱线图

3.1.4 电压稳定度

IEEE 30节点系统的初始电压稳定度为4.528 4。不同的领导者比例下，樽海鞘群算法对IEEE 30节点系统的电压稳定度目标值优化结果见表4，不同领导者比例求电压稳定度目标值的箱线图如图4所示。

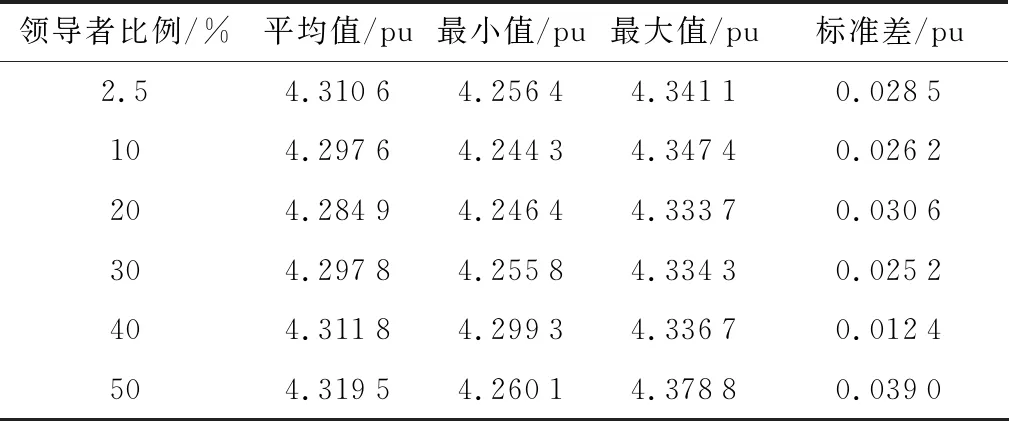
表4 不同领导者比例下IEEE 30节点系统电压稳定度目标值优化结果

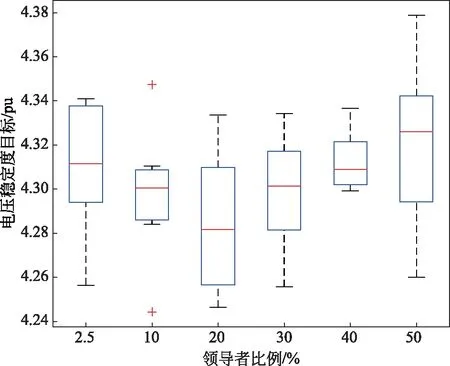
图4 不同领导者比例下樽海鞘群算法求解IEEE 30节点系统电压稳定度目标值的箱线图

总的来说，在IEEE 30节点系统的4个单目标优化问题上，将樽海鞘群算法的领导者取为种群中适应度值较好的20%或30%个体时，最优潮流计算可以取得相对更好的结果，而原算法中将领导者取为种群中最优个体的设置在各目标下求得的优化结果均较差。

3.2 IEEE 30节点系统(多目标优化)

使用多目标樽海鞘群算法同时优化IEEE 30节点系统的网损和电压偏移2个目标，算法种群规模和迭代次数不变，设置存储池可存储的解的上限为20。根据单目标优化结果，比较多目标樽海鞘群算法将领导者比例取为20%(记为A策略)、30%(记为B策略)和将领导者取为种群最优个体(记为C策略)对求解结果的影响。3种不同的领导者选取策略下，独立运行10次取平均值，求得的帕累托最优解集如下图5所示。

由图5可见，A策略、B策略较C策略均获得了支配性更好的帕累托最优解集。定量计算可得3种策略相对彼此的C指标见表5。

由表5可见，C策略所获得的帕累托最优解集有100%的解被A策略所获得的帕累托最优解集所支配，且有65%的解被B策略所获得的帕累托最优解集所支配。反之A策略、B策略获得的帕累托最优解集均没有解被C策略所获得的帕累托最优解集所支配。这说明将领导者比例取为适当比例的原则在多目标优化问题上仍然适用。

计算时间方面，在IEEE 30节点系统的网损、电压偏移和发电成本3个单目标优化问题上，单次最优潮流计算耗时约为55 s。在电压稳定度目标的优化问题上，单次最优潮流计算耗时约为65 s。IEEE 30节点系统多目标最优潮流计算耗时约为118 s。

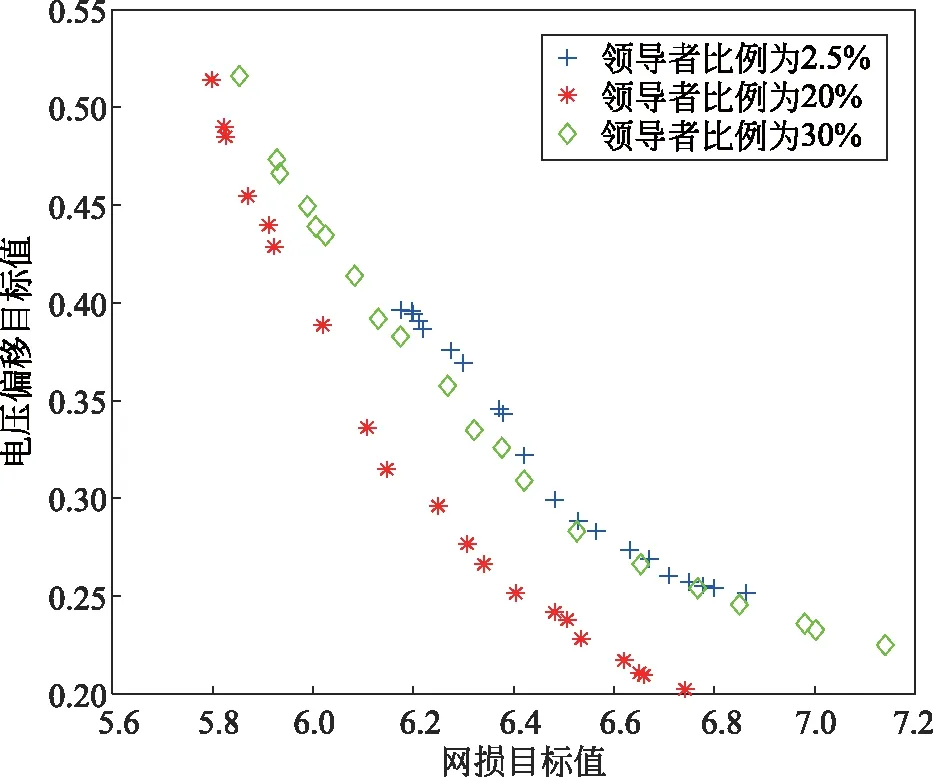
图5 不同领导者比例下樽海鞘群算法求解多目标优化问题的帕累托解集对比(IEEE30节点系统)

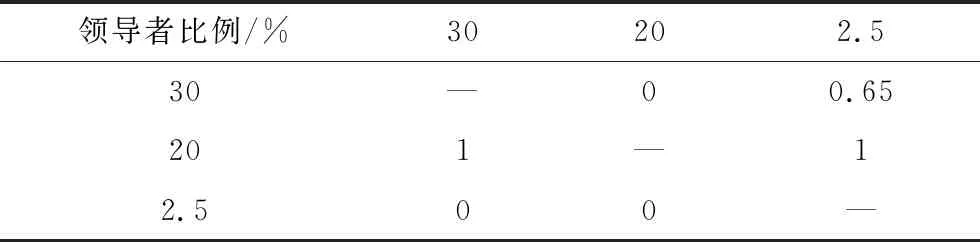
表5 不同领导者比例下的C指标

3.3 IEEE 118节点系统(单目标优化)

为验证将樽海鞘群算法领导者取适当比例的策略在较大电力系统中是否仍然适用，对IEEE 118节点系统进行最优潮流计算，该系统参数、控制变量和状态变量约束、罚因子取值见文献[23]，将负荷节点的电压约束由[0.9,1.1]改为[0.95, 1.1]。该算例初始惩罚项为4.580。算法种群规模仍取40，迭代次数取为1 000。各种领导者比例下独立运行10次并统计计算结果。

3.3.1 系统网损

IEEE 118节点初始系统网损为132.863 MW。不同的领导者比例下，樽海鞘群算法对IEEE 118节点系统的网损目标值优化结果见表6，不同领导者比例求网损目标值的箱线图如图6所示。

3.3.2 电压偏移

IEEE 118节点系统的初始电压偏移为1.439。不同的领导者比例下，樽海鞘群算法对IEEE 118节点系统的电压偏移目标值优化结果见表7，不同领导者比例求电压偏移目标值的箱线图如图7所示。

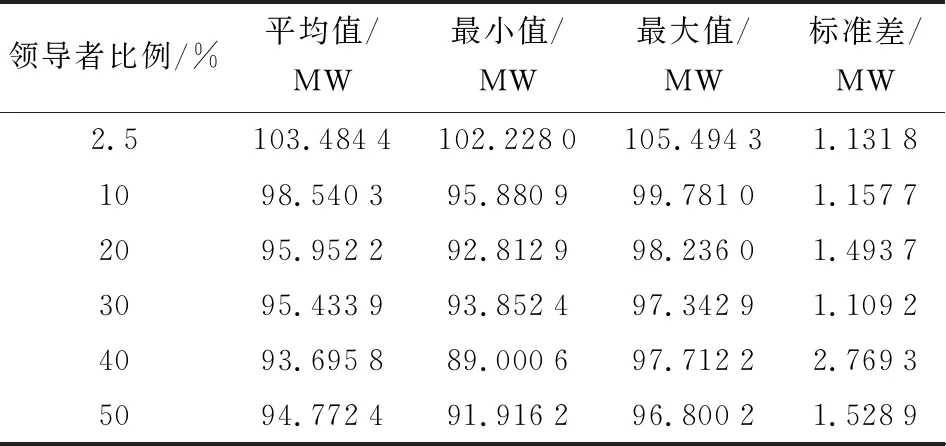
表6 不同领导者比例下IEEE 118节点系统网损目标值优化结果

图6 不同领导者比例下樽海鞘群算法求解IEEE 118节点系统网损目标值的箱线图

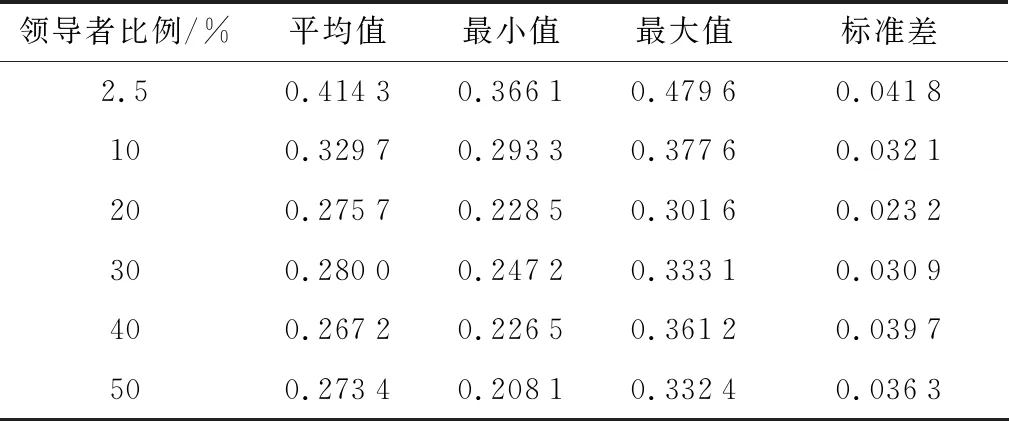
表7 不同领导者比例下IEEE 118节点系统电压偏移目标值优化结果

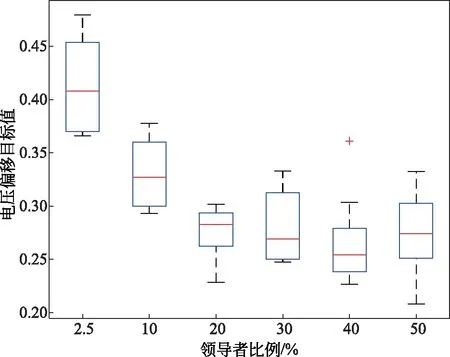
图7 不同领导者比例下樽海鞘群算法求解IEEE118节点系统电压偏移目标值的箱线图

3.3.3 发电成本

IEEE 118节点系统的初始发电成本为131 225 $/h。不同的领导者比例下，樽海鞘群算法对IEEE 118节点系统的发电成本目标值优化结果见表8，不同领导者比例求发电成本目标值的箱线图如图8所示。

表8 不同领导者比例下IEEE 118节点系统发电成本目标值优化结果

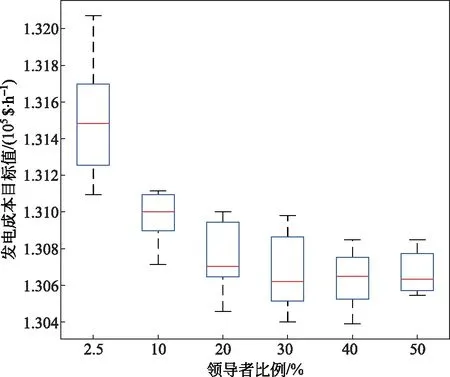
图8 不同领导者比例下樽海鞘群算法求解IEEE 118节点系统发电成本目标值的箱线图

3.3.4 电压稳定度

IEEE 118节点系统的初始电压稳定度为5.423 3。不同的领导者比例下，樽海鞘群算法对IEEE 118节点系统的电压稳定度目标值优化结果见表9，不同领导者比例求电压稳定度目标值的箱线图如图9所示。

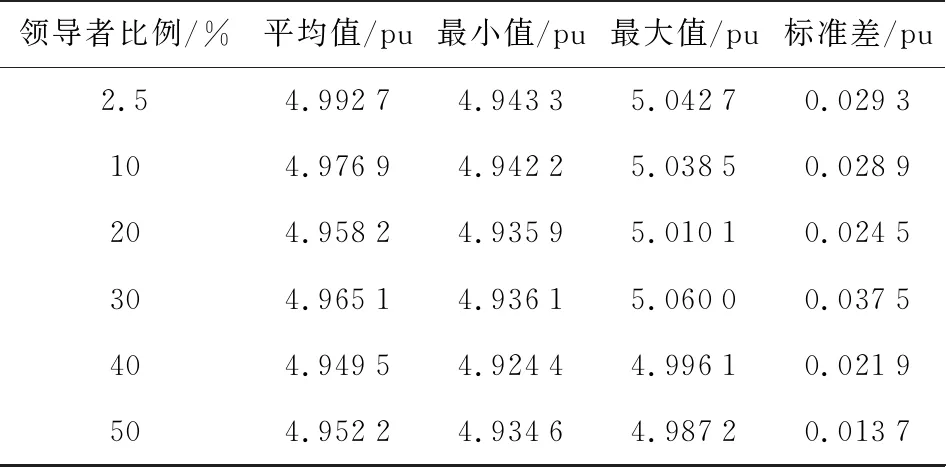
表9 不同领导者比例下IEEE 118节点系统电压稳定度目标值优化结果

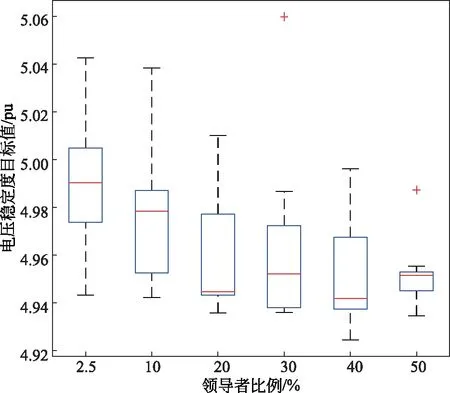
图9 不同领导者比例下樽海鞘群算法求解IEEE118节点系统电压稳定度目标值的箱线图

总体上看，在IEEE 118节点系统的4个单目标优化问题上，将樽海鞘群算法的领导者比例取为种群中适应度值较好的40%时，最优潮流计算可以取得相对更好的结果。

3.4 IEEE 118节点系统(多目标优化)

使用多目标樽海鞘群算法同时优化IEEE 118节点系统的网损和电压偏移2个目标，算法种群规模和迭代次数不变，设置存储池可存储的解的上限为20。根据单目标优化结果，比较多目标樽海鞘群算法将领导者比例取为40%(记为A策略)和将领导者取为种群最优个体(记为B策略)对求解结果的影响。2种不同的领导者选取策略下，独立运行10次取平均值，求得的帕累托最优解集如下图10所示。

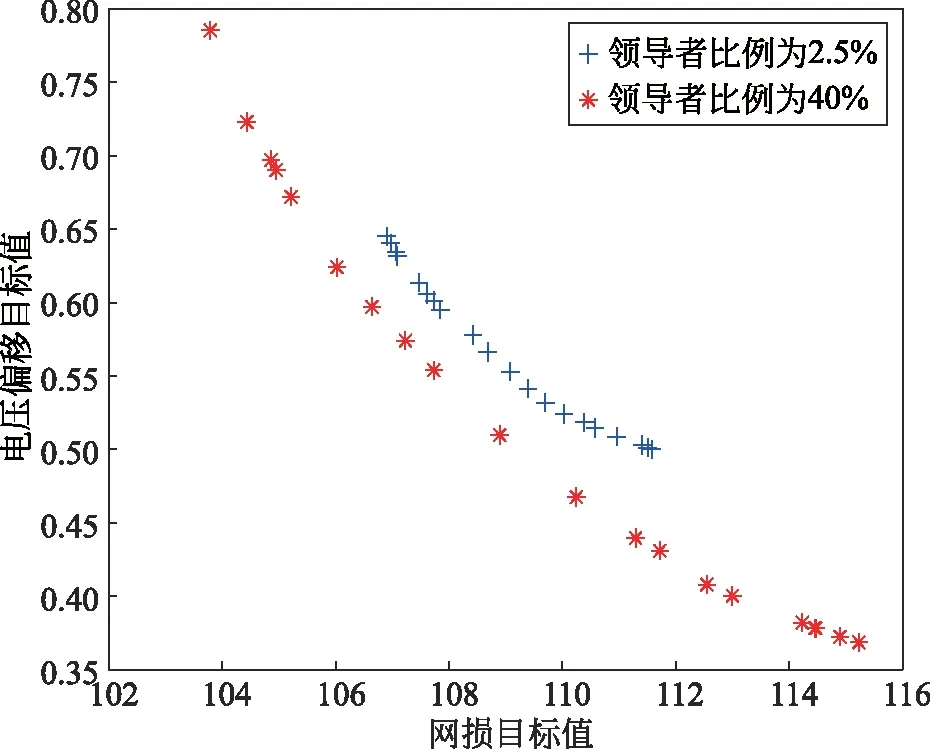
图10 不同领导者比例下樽海鞘群算法求解多目标优化问题的帕累托解集对比(IEEE 118节点系统)

可见，A策略较B策略获得了更好且分布更广的帕累托最优解集。定量计算可得，A策略所获得的帕累托最优解集较B策略所获得的帕累托最优解集的C指标为1，即B策略所获得的帕累托最优解集被A策略所获得的帕累托最优解集完全支配。再次验证了将领导者取为适当比例对樽海鞘群算法寻优效果的重要意义。

计算时间方面，在IEEE 118节点系统的网损、电压偏移和发电成本3个单目标优化问题上，单次最优潮流计算耗时约180 s。在电压稳定度目标的优化问题上，单次最优潮流计算耗时约310 s。IEEE 30节点系统多目标最优潮流计算耗时约390 s。

4 结论

本文将樽海鞘群算法用于求解IEEE 30节点系统及IEEE 118节点系统的最优潮流问题，以系统网损、电压偏移、发电成本和电压稳定度为目标，研究了将领导者取种群中最优个体或取种群中适应度较好的前10%～50%的个体对算法求解单目标和多目标最优潮流问题的优化效果的影响。总的来说，对于IEEE 30节点系统，将樽海鞘群算法中的领导者比例取为种群中适应度较好的前20%或30%时，较算法原有的将领导者取种群中最优个体的更新策略，可以取得相对更好的最优潮流求解结果；对于IEEE 118节点系统，将樽海鞘群算法中的领导者比例取为种群中适应度较好的前40%时，较算法原有的领导者取种群中最优个体的更新策略，可以取得相对更好的最优潮流求解结果。

需要说明的是，无论是领导者取种群最优个体还是取适度比例的樽海鞘群算法，均存在计算结果标准差偏大、鲁棒性欠佳的缺点。如何改进和提高樽海鞘群算法的计算鲁棒性是值得下一步继续研究的方向。