UFMC-MIMO系统中一种干扰消除算法

王 丹，杨 恒，石贝贝

(重庆邮电大学通信与信息工程学院，重庆 400065)

0 引言

5G新空口技术带领人类走向一个万物互联的时代，即物联网(Internet of Things, IOT)和机器通信(Machine Type Communication, MTC)[1]时代。目前正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术因其显著的抗干扰性能和简单有效的实现性，仍是主流调制技术之一。随着IOT与MTC通信的海量增加，OFDM逐渐暴露其缺陷与不足，大规模的、突发的、低时延的通信，不宜采用对定时和频偏敏感的OFDM技术[2]。虽然OFDM的循环前缀(Cyclic Prefix, CP)提高了它的抗干扰性，但在有限的频谱资源中，无疑降低了信道资源利用率。

4G中MIMO技术与OFDM的结合，克服了信道衰落、增加了系统容量及提高了频谱利用率，成为了4G关键技术之一[3]。然而，OFDM的缺陷并没有因其与MIMO技术结合而得到改善或消除，对定时和频偏的敏感，随时可能受到信道或其他潜在的影响而破坏载波间的正交性，造成严重的符号间干扰和子载波间干扰。针对5G通信场景需求，研究人员提出了滤波器组多载波技术(Filter-Bank Multi-Carrier, FBMC)、通用滤波多载波(Universal Filtered Multi-Carrier, UFMC)等候选波。FBMC通过对每一个载波滤波抑制旁瓣，显著增加了系统的抗干扰能力，缺点是对每个载波滤波造成了滤波器过长，增加了通信时延。另外，FBMC需要与OQAM技术结合，导致与现有技术的不兼容。文献[4]首次提出了UFMC，它综合了FBMC和OFDM的特点，对载波进行子带划分、进行滤波，不仅缩短了滤波器长度,还降低了对定时频偏的敏感，同时还证明了UFMC在上行多点协作系统中不管是定时同步还是频率偏差，其性能都胜过OFDM。最重要的是，QAM可以适用于UFMC，同样可以依靠基于快速傅里叶变换(Fast Fourier Transform, FFT)的接收处理和载波均衡，本质上与OFDM非常接近，能与各种MIMO系统兼容。

在单输入单输出(Single Input Single Output, SISO)系统中，对UFMC的研究已相当成熟，而与MIMO结合的场景并未获得太多关注。无论是SISO场景还是MIMO场景，波形调制的关键都是其抗干扰性和如何消除干扰。针对SISO场景，文献[5]提出了一种最大化信号带外泄露比(SLR)算法优化滤波器系数；文献[6]基于最小均方(LMS)算法，提出了一种自适应频偏消除方案，通过对2N-FFT的接收信号进行多次迭代优化滤波器系数，直至频率偏移误差达到最小；文献[7]提出了一种联合干扰消除算法，首先利用最小二乘法(LS)计算大频偏，再利用两个相同的训练符号进行精确估计。与SISO场景相比，涉及UFMC-MIMO的文献并不多，其中文献[8]提出了一个包括UFMC-MIMO系统发射机、接收机和波束成形的实现算法，通过仿真证明了该方案能正确的收发数据；文献[9]分析了UFMC-MIMO系统的抗载波频偏性能，并与OFDM-MIMO系统作了仿真比较，证明了UFMC-MIMO的鲁棒性明显优于OFDM-MIMO。上述两种算法均未考虑过信道定时频偏对信号的影响或提出信号定时频偏的估计补偿算法。本文基于Walsh码提出了一种针对UFMC-MIMO系统的干扰消除算法，通过设计特殊的训练结构，利用Walsh码的性质，不仅能进行定时频偏估计还能区分各个传输信道。最后，在2×2的UFMC-MIMO系统中进行仿真，结果表明该算法能够有效降低信号误符号率和显著提升系统的抗干扰性能。

1 系统模型

1.1 UFMC-MIMO系统

图1所示为2×2 UFMC-MIMO系统模型。其中包括预编码、UFMC发送端、空间信道和UFMC接收端和译码器。

图1 2×2 UFMC-MIMO系统模型

为了简便，省略了部分模块，且接下来的分析都是针对2×2 UFMC-MIMO系统模型。在图1中，原始数据流D首先经过预编码处理后得到输出信号流Xi=[Xi(0),Xi(1),…,Xi(N-1)](i=1,2)，其中N代表系统FFT大小，接着分别通过UFMC调制模块，最后由两根天线同时发射，且在信道传输过程中相互独立。通过信道H(针对本文模型，包括Hij(i,j=1,2))后被接收端两根天线接收。若仅分析接收天线j处接收信号，则信号表达式为

(1)

1.2 UFMC发送端和接收端

图2所示为UFMC系统的发送端和接收端，虽然与MIMO系统结合，但单独收发端信号传输过程没有太大差异。

图2 UFMC系统发送端和接收端

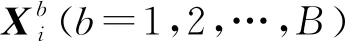
n=0,1,…,N-1

(2)

式中，K为每个子带中的载波数目。通过长度为L的滤波器后，所有子带信号叠加，得到发送信号为

(3)

式中,*表示线性卷积，{fb(0),fb(1),…,fb(L-1)}代表第b个滤波器的系数，所以UFMC符号长度为Nt=N+L-1。通过信道传输后到达接收端，经过时域均衡处理，再进行2N点FFT，若Nt<2N则补零，得到频域信号

(4)

2 Walsh序列同步算法

UFMC-MIMO系统因不同收发天线之间的信道相互独立，所以在接收端作定时同步的时候，还得正确区分发送天线。本节基于Walsh码设计特殊的训练符号，可以在作定时同步的同时还可以区分不同天线信道，最后对接收信号进行精确补偿，从而增强UFMC-MIMO系统的抗干扰性和鲁棒性。

2.1 Walsh序列结构设计

Walsh码属于正交码的一种，来源于H矩阵，根据H矩阵中“+1”和“-1”的交变次数重新排列就可以得到Walsh矩阵。Walsh码在码分多址系统(CDMA,WCDMA等)中一般被用于区分不同的信道，其中的码指的就是Walsh码[10]。图3所示为采用了Walsh码而设计的正交重复训练序列结构。

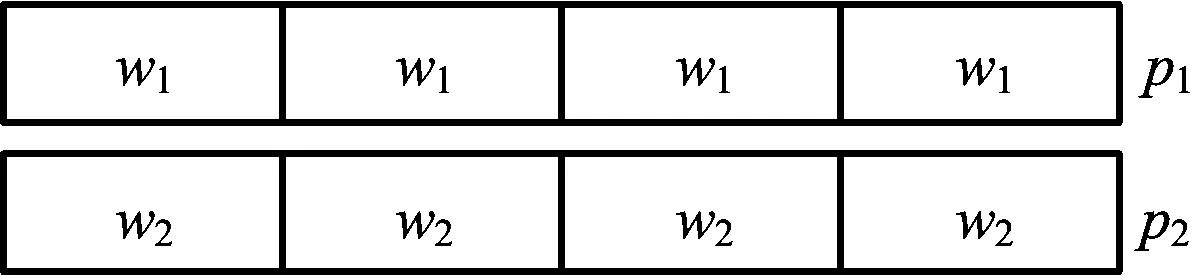
图3 Walsh训练序列结构

其中包括4个长度相同的Walsh码。本文讨论的是2×2 UFMC-MIMO系统，所以需要2组不同的Walsh码训练序列，不同Walsh码训练序列是正交的。在发送端，2根发送天线分别发射不同的训练序列，彼此正交，其中第i根天线发送的训练序列pi可以表示为

pi=[wiwiwiwi]

(5)

式中,wi表示Walsh码组，满足取任意的1≤i,j≤2有

(6)

2.2 符号定时同步

UFMC-MIMO系统进行符号定时同步时，需要利用Walsh码良好的自相关特性和处处为零的互相关特性。对一根接收天线j分析，如果本地已知发送端天线发送的正交序列集合{pi}，就可以任意取集合中的一个发送序列pi进行相关计算，得

(7)

式中,Tw表示Walsh码的长度，yj表示第j根接收天线接收到的训练序列，则第j根天线的符号定时τj可由上得到

(8)

2.3 频偏估计

频偏估计是在获取定时同步后进行的，故2×2 UFMC-MIMO系统在第j根接收天线处收到的信号为

(9)

式中：cij代表第i根发送天线到第j根接收天线之间时域上的频率偏移，可写为

cij(k)=ej2πεijk/N(k=0,1,…,N+L-1)

(10)

εij代表第i根发送天线到第j根接收天线之间归一化的频偏，εij=Δfij/F(F代表子载波间隔)；si(n)代表第i根发送天线的发送信号，si(n)=pi(n)，n的取值范围为[0,4×Tw-1]；zj(n)表示天线j处的高斯白噪声。

在频偏估计中，需对发送端天线进行区分，将上面式(9)代入式(7)得

(11)

在式(11)中，Rij(t)是指第i组Walsh序列wi(n)与第j根接收天线的接收信号作相关得到。t的范围为0≤t≤Tnw-1，Tnw指的是Walsh序列中Walsh码的重复次数。由Walsh码的正交性可以得到

(12)

代入式(11)中可以简化为

(13)

从上面公式可以看出，Rij(t)里面涉及第i根发送天线与第j根接收天线的频偏εij。接着进一步推导，则Rij(t)的自相关Rd为

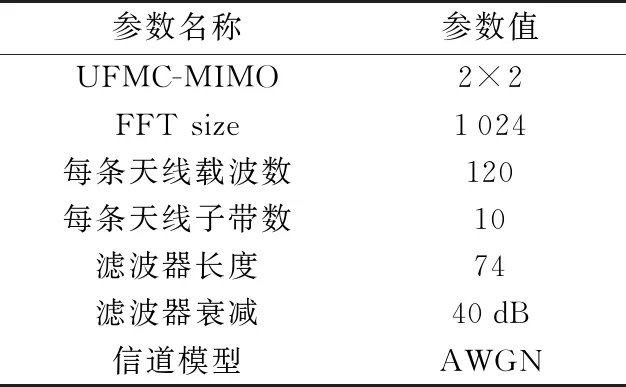
式中，1≤a

arg(Rdij)=-2πTwdεij/N

(15)

所以推导频偏εij为

(16)

由此，将第j根接收天线的信号与发送端的各个训练结构pi进行上述相关计算，可以获得对应信道路径的频偏ε1j,ε2j。则对于2×2 UFMC-MIMO系统同理，我们可以计算出2×2组频偏:

(17)

计算出频偏后，在进行2N点快速傅里叶变换之前在时域进行补偿，补偿后信号为

rj(n)=yj(n)·e-j2πεij/N

(18)

如此则可以降低或消除信道对信号传输的干扰。

3 仿真与分析

仿真分析主要是针对2×2 UFMC-MIMO系统，环境为服从高斯分布的基本噪声与干扰模型，输入数据可以使用MQAM星座映射。通过配置不同的载波频率偏移(CFO)参数，观察补偿后接收端信号的误符号率(SER)判断补偿效果。具体系统参数配置如表1所示。

表1 系统仿真参数

如图4所示，在AWGN信道中，信噪比(SNR)不变时，随着信道 CFO的增加，SER上升越来越明显。CFO固定时，增加SNR可以明显降低系统误符号率。

图4 无补偿各频偏误码率

如图5所示，在本文提出的定时频偏算法下，假设信号已完成符号定时。首先计算出信道的频偏估计值，再在接收端对时域信号进行一定补偿。可以看出，在频偏范围较小的时候，误符号率非常接近无频偏状态，补偿效果明显。相比较而言，当频偏偏大时，补偿只能降低误符号率，效果没有低频偏时显著，但也在一定程度上提高了系统的抗干扰性。

图5 频偏补偿后误码率

4 结束语

UFMC-MIMO系统各发送天线与接收天线之间的传输信道存在差异，所以不同信道频偏可能也不同。本文针对2×2 UFMC-MIMO进行了详细的分析，从整体系统模型到单链路的UFMC系统链路，并提出了一种适用于UFMC-MIMO系统中定时频偏估计算法。该算法主要是基于Walsh码构成的训练序列，通过利用Walsh码的正交性及相关性进行各信道的符号定时和频偏估计，最后通过Matlab仿真分析。仿真结果表明，通过该算法在信号接收处进行补偿，能够在一定程度上降低或消除由定时或频偏引起的干扰，降低误符号率。此外，该方法也可以扩展应用到更大的M×NUFMC-MIMO系统中，为以后UFMC-MIMO系统的进一步研究提供参考。