LFM-PC复合调制信号优化设计算法

李 晨，张劲东，丁 逊，尚东东

(南京航空航天大学电子信息工程学院，江苏南京 211100)

0 引言

PC信号因其分辨率、测量精度较高的优点被广泛应用，但是只能被运用于窄多普勒频移的场合，并且形式简单，抗干扰能力一般。基于LFM信号和PC信号复合调制的LFM-PC信号，兼顾了两种信号的优点，具有较高的分辨率、测量精度，同时扩展了PC信号的多普勒容限，还可以提高信号的复杂程度，从而提高雷达系统的抗干扰能力。

为了使PC信号获得接近理想的主副瓣比，国内外学者研究了多种启发式优化算法进行优化设计，主要包括遗传算法[1]、模拟退火算法[2]、基于飞蛾扑火的改进方法[3]、改进的蚁群算法[4]等。以上几种智能搜索算法较为容易实现，但是因其随机性先天存在速度慢，效果一般等问题。除了启发式优化算法以外，冯日博等[5]提出了一种基于新循环算法(Cyclic Algorithm-New, CAN)的优化方法。该方法将峰值旁瓣的最小化等价为一个频域最小化问题，进而转化为一个二次函数的最小化问题。李旭等[6]在利用CAN算法优化PC信号自相关函数的基础上，提出了适用于优化正交波形互相关特性的MultiCAN算法。Kerahroodi等[7-8]将坐标下降法(Coordinates Down, CD)应用到PC信号优化设计中，CD算法在每次迭代过程中使用不同的坐标方向，在当前点处沿一个坐标方向进行一维搜索以求得目标函数的局部最小值。

传统的LFM-PC信号在脉间实现相位编码调制，脉内实现线性频率调制。而本文研究的LFM-PC信号在脉内实现线性频率和相位编码复合调制。对该种信号的优化设计还处于起步研究阶段，Majumder等[9]利用Walsh正交码实现脉内相位编码调制。吴悦[10]利用LFM-PC信号来设计正交波形，并提出了基于模糊函数的抗欺骗干扰波形设计模型，采用共轭梯度法和交替迭代算法求解优化模型。但是其优化设计的调制相位为连续相位，对离散相位调制缺少研究。

本文针对PC信号在高速运动平台和高速目标探测中运用存在多普勒敏感问题，研究了一种宽多普勒容限的LFM-PC复合调制信号。首先，简单介绍了LFM-PC信号，并给出了其模糊函数离散表达式。接着，在多普勒容限内以最小归一化积分旁瓣为准则建立优化模型，采用基于ADMM的低复杂度方法求解优化模型。仿真结果表明，此算法相比遗传算法速度更快、效果更佳。优化之后的LFM-PC信号在保持宽多普勒容限的同时具有更低的归一化旁瓣，因此相比PC信号可以在多普勒失谐时具有更高的分辨率、测量精度。

1 信号模型

1.1 时域波形

PC信号复包络[11]可表示为

(1)

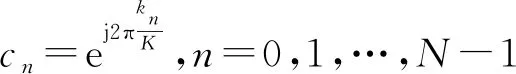
在PC信号上复合调制一个LFM信号uLFM(t)=ejπμt2,0≤t≤T，其中μ表示调频斜率，则LFM-PC复合调制信号表示为

uLFM-PC(t)=uLFM(t)·uPC(t)=

(2)

1.2 模糊函数

模糊函数定义式[11]为

(3)

(4)

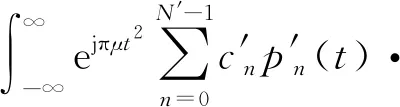
(5)

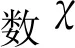
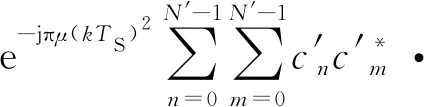
(6)

取f=μpTS, -(N′-1)≤p≤N′-1

(7)

(8)

式中，

Jk表示转移矩阵：

2 模糊函数优化

2.1 优化算法

ADMM算法[12]是一种求解优化问题的计算框架，适用于求解具有分布式结构的凸优化问题。ADMM通过分解协调过程，将大的全局问题分解为多个较小、较容易解决的局部子问题，并通过协调子问题的解而得到大的全局问题的解。

ADMM求解问题的表达式为

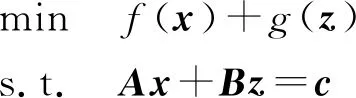
(9)

将其改为增广拉格朗日函数，ρ为惩罚项系数，有

Lρ(x,z,λ)=f(x)+g(z)+λT(Ax+Bz-c)+

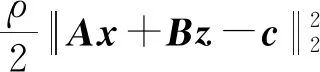
(10)

u(t+1)=u(t)+Ax(t+1)+Bz(t+1)-c

(11)

2.2 优化模型

LFM-PC信号模糊函数的离散表达式由式(8)表示。其主峰幅度可表示为

|χLFM-PC(k0,p)|=|c′HH(k0,p)c′|=

(12)

式中，-(NS-1)≤p≤(NS-1)。当p确定时，|χLFM-PC(k0,p)|为一定值。定义主峰幅度下降3 dB的范围为多普勒容限(Doppler Tolerance, DT)，则多普勒容限内的归一化模糊函数可表示为

-(N′-1)≤k≤(N′-1),-NDT≤p≤NDT

(13)

式中，NDT<(NS-1)表示多普勒容限对应的范围。

为了提高雷达在信号存在多普勒失谐场景中的探测性能，优化问题可描述为：在多普勒容限内以最小化归一化积分旁瓣为准则，优化LFM-PC模糊函数，优化范围为Ψ=[(k,p)|NS≤|k|≤N′-1,0≤|p|≤NDT]。其目标函数由归一化积分旁瓣NISL表示为

(14)

2.3 优化过程

利用ADMM架构嵌套拟牛顿法优化目标函数式(14)，优化问题为

(15)

在式(15)中引入辅助变量z和约束条件c=z，即

(16)

式(15)和式(16)等价。取u=(λr+jλi)/ρ，根据式(16)写出增广拉格朗日方程：

(17)

记c(t)为第t次ADMM迭代后的c值(z和u相应地记为z(t),u(t))，给定初值c(0),z(0),u(0),则该问题的求解可按照如下步骤进行：

1) 更新c，此时z(t),u(t)看作已知量

该问题为无约束最优化问题，可使用拟牛顿法求解。

2) 更新z，此时c(t+1),u(t)看作已知量

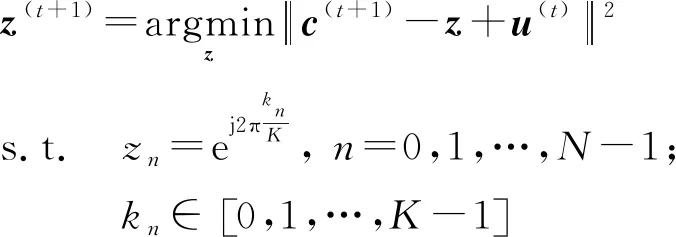
(19)

式(19)中元素z彼此独立，则可将其分解为N个子问题，子问题可表述为

(20)

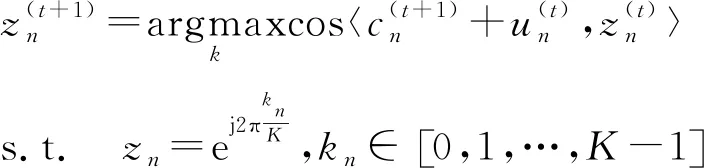
(21)

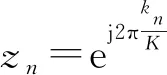
(22)

则式(19)的解为

(23)

3) 更新u

u(t+1)=u(t)+c(t+1)-z(t+1)

(24)

由此，ADMM算法的基本思路：初始化变量c(0),z(0),u(0)，接着重复步骤1)到步骤3)直至满足迭代停止条件(迭代次数达到上限或者|NISL(t+1)-NISL(t)|≤ε，ε为一个较小的正数，作为收敛门限)。以上，输出优化后的结果。

表 1给出利用交替方向乘子法求解优化模型的步骤。

表1 ADMM步骤

3 仿真及结果分析

取码长N=60，调频斜率μ=6×1012，调制相位数K=2/4/8，分别通过100次的蒙特卡洛实验，计算PC信号、LFM-PC信号的多普勒容限DT。由表2可知，LFM-PC信号DT明显优于PC信号。

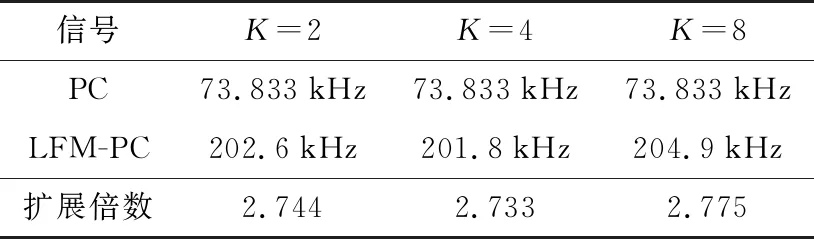
表2 PC信号与LFM-PC信号多普勒容限对比

将平均积分旁瓣(Average Integral Side Lobe, AISL)和平均归一化积分旁瓣(Average Normalized Integral Side Lobe, ANISL)定义为

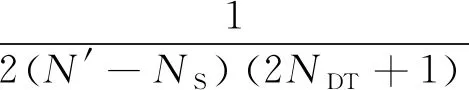
(25)

(26)

式中，Ψ=[(k,p)|NS≤|k|≤N′-1,0≤|p|≤NDT]表示多普勒容限DT内的旁瓣范围。

仿真得到LFM-PC信号的多普勒容限DT后，在范围DT内分别计算PC信号的平均积分旁瓣AISL，LFM-PC信号的平均积分旁瓣AISL、平均归一化积分旁瓣ANISL。由表 3可知，两种信号AISL基本相等，但是LFM-PC信号模糊函数经过归一化处理之后，其ANISL值高于PC信号AISL，这说明多普勒失谐时，脉压副瓣增高，雷达探测性能恶化。

表3 PC信号与LFM-PC信号模糊函数旁瓣对比

为了提高多普勒失谐时的雷达探测性能，在多普勒容限内以最小归一化积分旁瓣为准则对LFM-PC信号模糊函数进行优化。设置迭代次数上限为100次，分别用上述ADMM算法以及GA算法对相同的初始信号进行优化。初始信号ANISL=-20.353 2 dB。经过迭代后，优化前后仿真结果如图 1和图 2所示。

图1 优化前模糊函数

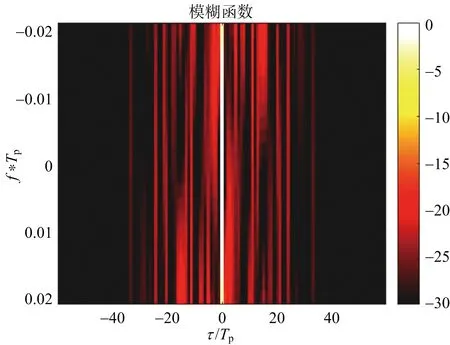
(a) K=2 ADMM优化

从表4可以看出，经过ADMM算法、GA算法优化的LFM-PC信号相比于未优化的信号，ANISL均明显下降。尤其是ADMM算法，随着相位数的增加，其优化效果比GA算法优化效果愈发显著。同时观察图 3的优化算法迭代收敛曲线，我们可以发现ADMM算法相比于GA算法收敛更快、效果更好。

表4 ADMM算法与GA算法优化ANISL对比

对比表3和表4可知，优化之前的LFM-PC信号ANISL不及PC信号AISL，优化之后的LFM-PC信号ANISL明显优于PC信号AISL值。因此，优化前后的LFM-PC信号在多普勒失谐情况下探测性能显著提升，具有比PC信号更宽的多普勒容限的同时还具有更高的分辨率和测量精度。

图3 ADMM算法与GA算法优化收敛曲线对比

4 结束语

基于LFM信号和PC信号复合调制的LFM-PC信号，具有比PC信号更宽的多普勒容限。本文利用ADMM算法，以最小归一化积分旁瓣为准则，优化LFM-PC信号模糊函数。对比GA算法仿真结果表明，ADMM算法是一种收敛速度快、运算量低的优化算法。经过优化之后的LFM-PC信号，在宽多普勒容限的基础上同时具有更低的归一化积分旁瓣。因此，经过优化的LFM-PC信号相比PC信号可以在高速运动平台和高速目标探测中具有更高的分辨率和测量精度。