空间目标的雷达定轨实时识别问题研究
2021-03-30黄晓斌石斌斌
黄晓斌,张 燕,肖 锐,石斌斌
(空军预警学院,湖北武汉 430019)
0 引言
反导预警雷达在弹道导弹探测模式下,可观测到许多低轨空间目标。由于反导预警雷达作战使命的定位,对于观测到的空间目标数据往往直接丢弃,这造成了雷达使用效率的降低,并对雷达操作人员想进一步了解空间目标的特性造成困难。为此,本文提出了一种基于空间目标轨道根数的目标识别方法,该方法将雷达定轨所得轨道根数与空间目标数据库中的轨道根数进行匹配,从而对目标进行快速识别。此外,依据该方法开发了一套空间目标实时识别软件,帮助雷达操作员快速了解目标的属性信息。
对空间目标的快速捕获识别与高精度跟踪监视是利用并控制空间资源的前提和基础[1]。自20世纪50年代开始雷达目标识别的相关研究就开始出现,其主要原理是通过对雷达观测信号回波进行分析和处理,从中提炼典型数据或者特征标识,从而对目标属性进行识别和判断,早期的雷达目标识别研究是基于目标RCS的测量来进行,随着技术发展,越来越多可用于目标识别的信息被不断挖掘出来,相关研究和应用技术也不断出现,例如基于回波调制谱特征的目标识别技术、基于目标极点分布特征的识别技术、基于目标回波极化特征的目标识别技术[2]、高分辨率雷达目标成像识别[3]等。近年来,随着雷达装备技术的快速进步,越来越多的雷达具备了空间目标探测的能力,针对空间目标识别技术的需求也逐渐增大,而空间目标的轨道特性因其可量化,对雷达波束特性依赖小,受大气层和电离层影响小等特点,非常适合进行空间目标识别。
本文的主要内容包括基于轨道根数的空间目标识别所涉及的基本数学原理、程序设计思路和利用仿真与实测数据验证软件的有效性。
1 基于轨道根数的空间目标识别数学原理
基于轨道根数的空间目标识别处理流程如图1所示,包括坐标转换、初轨确定、轨道改进和轨道匹配四个步骤。

图1 基于轨道根数的空间目标识别处理流程
1.1 坐标转换
雷达观测基于地球坐标系,空间目标轨道是基于天球坐标系,这就涉及到地球坐标系与天球坐标系之间的转换。
协议天球坐标系由国际天文联合会(IAU)和国际地球自转和参考系服务(IERS)发布,目前采用的是国际天球参考系(ICRS)。依据坐标原点的不同,ICRS可分为太阳系质心天球参考系(BCRS)和地球质心天球参考系(GCRS)。BCRS用于计算行星的运动轨道,编制星表;GCRS用于计算卫星轨道,编制卫星星历。ICRS由国际天球参考框架(ICRF)来实现。1997年IAU第23届大会上,通过并决定自1998年1月1日起,在天文研究、空间探测、大地测量以及地球动力学等领域中采用ICRS[4]。
协议地球坐标系由国际地球参考系(ITRS)实现。GCRS是一个相当好的准惯性系,卫星的轨道计算一般都是在GCRS中进行。这就必须涉及到GCRS与ITRS间的坐标转换问题[5]。
1) 站心地平坐标系Xh与ITRS坐标系XGO的转换
站心地平坐标系Xh与ITRS坐标系XGO的定义如表1所示,它们之间的转换公式为
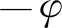
(1)
式中:算子Rn(θ)表示绕n轴(n=1,2,3分别对应x,y,z三个轴)转动角的坐标变换矩阵;P2=diag[1,-1,1];λ,φ为测站的天文经纬度,而测站在ITRS坐标系中的直角坐标XGOC由测站的地理经纬高坐标(B,L,H)计算[6]。关于天文经纬度和地理经纬度的区别见文献[7]。
2) ITRS与GCRS坐标系的转换
ITRS与GCRS的转换早期是基于春分点的。目前,IERS(2010)建议使用基于无旋转原点(NRO)的转换方法[7]。基于IAU 2006/2000A-CIO模型的转换流程[7]如图2所示。转换过程中涉及两个中间坐标系:地球中间坐标系(TIRS)和天球中间坐标系(CIRS),它们的定义见表2。
在t时刻,ITRS和GCRS的转换是两个三维直角坐标系间的转换,可以写成
XGCRS=M(t)RCIO(t)W(t)XITRS
(2)
式中,M(t)、RCIO(t)和W(t)分别为由于CIP在GCRS中的运动(岁差章动)、地球的自转以及CIP在ITRS中的运动(极移)引起的旋转矩阵。它们的具体表达式见文献[7]。

图2 “IAU 2006/2000A-CIO based”坐标转换流程
1.2 轨道确定
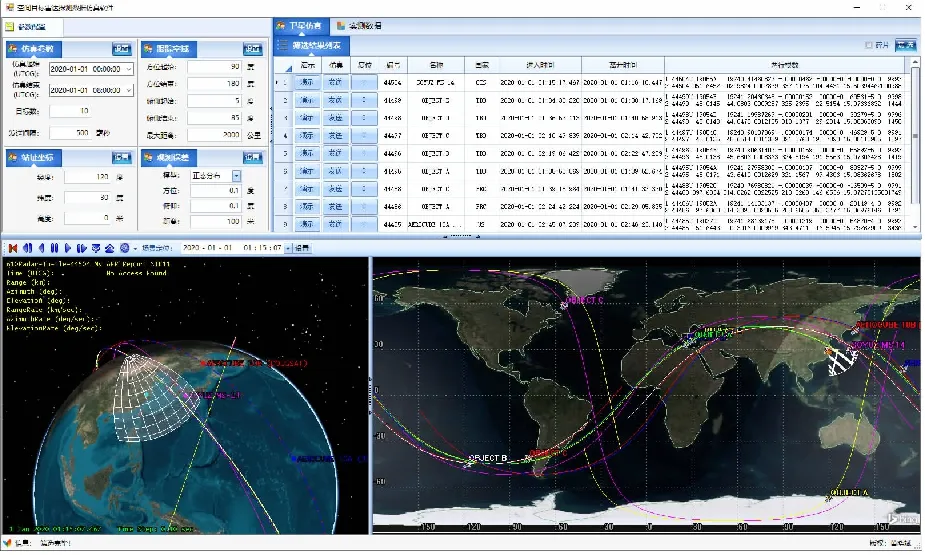
赫里克-吉布斯算法是雷达空间目标轨道确定中常用的一种初定轨方法。设在3个连续的时刻t1,t2和t3(t1 v2=-d1r1+d2r2+d3r3 (3) 式中, 表1 站心地平坐标系与ITRS坐标系的定义 表2 TIRS坐标系与CIRS坐标系的定义 轨道改进的基本流程图[9]如图3所示。 图3 轨道确定流程图 空间目标是沿着固有轨道运动的,它的6个轨道根数是决定其运行规律的主要参数,也是进行空间目标识别的基础。因此,空间目标的识别可以通过将观测数据与已知目标的轨道根数样本进行匹配来实现。首先给出匹配识别的公式如下: (4) 式中:δi为待识别目标相对样本目标的轨道根数误差,i=1,…,6分别表示半长轴a、偏心率e、倾角i、升交点赤经Ω、近地点幅角ω和升交角距L(可与真近点角进行互算)相对误差;wi(i=1,…,6)为6个加权系数,满足w1+w2+…+w6=1;T为比较门限。如果上式满足,则目标匹配成功。 首先定轨相对误差δi由下式计算: (5) (6) 则各轨道根数的权重系数wi可由下式计算获得: (7) 有了wi后,可以对这N个目标分别计算参数Tj(j=1,…,N): (8) 然后计算它的均值mT和标准差σT,则门限T可由下式计算获得: T=mT+(3~5)σT (9) 从上式也可以看出,轨道改进精度越高(即δi越小),我们进行轨道匹配的门限T就越小。 图4给出了基于轨道根数实时识别的程序设计流程图,为叙述方便,以图中给出的典型参数设置为例。其基本思路是在雷达任务规划席位通过内网UDP方式接收来自雷达显控席的目标点迹数据,通过坐标转换模块,将雷达测站的RAE数据转换为惯性坐标系下的XYZ数据,如果积累的点迹数据达到3个以后,首先判断是否有轨道根数,如果没有且点迹数大于20,则识别失败,程序结束;如果有轨道根数,但点迹数小于10,则执行初轨确定,每次初轨计算都取当前航迹的首、中、末三点,如果这三点计算失败,也可利用最新的三点数据计算;如果有轨道根数,但点迹数不是5的倍数,则继续获取新的点迹;如果有轨道根数,且点迹数是5的倍数,则执行轨道改进,改进后判断点迹数是否小于20,小于则获取新的点迹,否则进行轨道匹配操作,从本地空间目标轨道数据库中识别出空间目标。 图4 基于轨道根数的空间目标实时识别程序设计流程图 轨道数据仿真是本文研究的基础,因此在这部分中先简要介绍数据仿真工作,再利用仿真数据和实测数据验证目标识别算法的有效性。 本文开发了“空间目标轨道数据仿真软件”来模拟产生雷达对空间目标的观测数据,软件界面如图5所示。软件的“参数配置”考虑了仿真时段、雷达站址、跟踪空域和测量精度等信息;“目标信息区”显示筛选后符合要求的目标,可通过“演示”按钮在下方的二/三维态势中展示目标的运动特征以及雷达对目标的观测情况,并可通过“仿真”按钮模拟雷达按一定数据率向外发送目标的点迹信息。 图5 空间目标轨道数据仿真软件界面 开发的“空间目标实时识别软件”界面如图6所示,软件右上角手动输入需要实时识别的航迹批号,中部靠上部分显示定轨信息和识别结果,中部靠下部分是二/三态势图,下部是信息显示区。 图6 空间目标实时识别软件界面 按照上文中介绍的方法计算权重系数可得w1=0.402,w2=0,w3=0.293,w4=0.227,w5=0,w6=0.078;比较门限T=0.004。以下所描述的时间都是UTCG格式,即格林尼治协调世界时。 首先利用仿真数据验证软件的有效性,设定仿真时间段为2019-11-24T12:00:00至2019-11-25T12:00:00,利用“空间目标轨道数据仿真软件”筛选100颗卫星作为仿真数据,输入到“空间目标实时识别软件”中,经实时定轨和识别后全部正确。由于篇幅有限,表3列出了3颗卫星具体计算结果。 利用某型反导预警雷达于2019-11-21T00:55:09至2019-11-21T00:56:58对编号为33 320的目标实际观测的数据对软件进行验证。计算结果如表4所示。 表3 仿真数据目标识别结果 表4 实测数据目标识别结果 从表3和表4的数据看出,近地点幅角的误差比较大,这是因为对于近圆轨道,该参数的物理含义存在歧义[10]。 本文针对反导预警雷达的工作特点,介绍了基于轨道根数的空间目标识别的基本数学原理,其中包括坐标转换、轨道确定和轨道匹配等核心处理步骤及其方法;在此基础上,开发了一套空间目标实时识别软件,介绍了软件的程序设计思路;最后,本文分别通过仿真数据和实测数据验证了本文空间目标识别算法的有效性。其中仿真数据来源于空间目标轨道数据仿真软件,实测数据来源于某型反导预警雷达对已知轨道根数目标的真实观测数据,仿真和实测数据的目标识别结果表明,本文提出的空间目标识别算法是确实有效的。下一步我们将进一步研究基于人工智能技术的在线自适应策略调整加权系数w和门限T。


1.3 轨道匹配
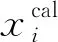
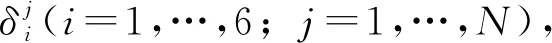

2 程序设计
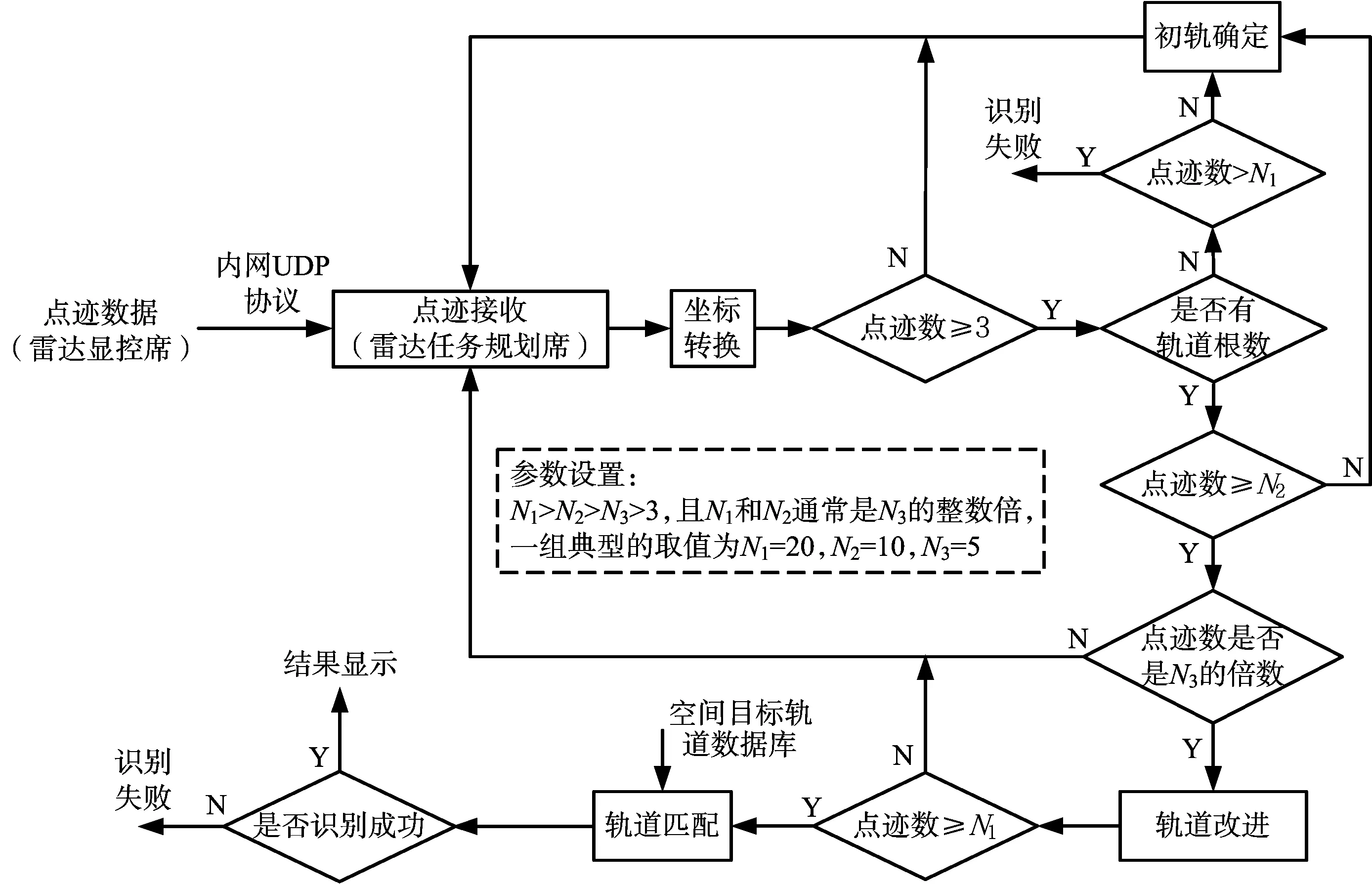
3 仿真实验
3.1 数据仿真
3.2 目标识别



4 结束语
