FSAE赛车立柱的优化设计
2021-03-30黎静远钟玉华张志坚张世鑫
黎静远,钟玉华,张志坚,张世鑫
(华南理工大学广州学院汽车与交通工程学院,广东广州 510800)
0 引言
FSAE赛车通常采用不等长双叉臂的悬架形式,立柱(转向节)则是连接悬架上下控制臂及承载车轮、制动卡钳的重要部件,其在任何工况下都必须具有足够的强度和刚度来保证汽车运行的稳定性。此外,立柱还属于非簧载质量,减轻非簧载质量有利于提高悬架系统的响应,使赛车的操纵稳定性得到较大改善。所以在保证强度和刚度的前提下,为了获得更加轻量化的立柱,许多研究人员从立柱的制造加工和立柱的强度、刚度校核这两个方向进行研究。文中对立柱的研究属于第二个方向[1]。
2008年,和进军[2]采用Adams car模块建立整车多体动力学仿真模型,并编写相应的路面控制文件,对模型进行动力学仿真。将获得的极限工况数据导入Ansys中进行静力学分析,验证赛车立柱是否符合使用要求。
2015年,汪随风等[3]使用LMS中MOTION模块建立整车动力学模型,以车辆轴头六分力传感器采集的道路载荷谱为信号,建立车辆轮心力响应与TWR虚拟台架作动器位移之间的传递函数,并使用虚拟迭代的方法反求出车辆在道路下的虚拟台架作动器的位移,并以此为台架提供信号驱动台架,提取转向节在该路况下的边界载荷谱,为立柱疲劳耐久性能分析提供输入数据。
2015年,GARY[4]通过计算车轮上跳最大时的车轮载荷,进一步求出立柱极限工况下的载荷。并利用Ansys静力学模块对立柱进行性能校核,得出立柱的应力和应变。从耐久测试比赛获取车轮历史载荷数据,将其导入Ansys nCode模块中进行疲劳分析。仿真结果作为立柱拓扑优化的重要依据。
文中通过整车动力学仿真,获取赛车轮胎的极限载荷。计算出后立柱的受力,对其进行静力学分析。基于分析结果对后立柱结构进一步优化,延长使用寿命。
1 赛车整车动力学仿真
1.1 整车动力学模型搭建
使用VI-GRADE中的SuspensionGen模块,通过输入硬点和悬架参数(表1)的方式建立结构化的悬架模型如图1所示。该模块主要是对悬架几何进行运动学分析,不考虑动力学特性,所以悬架所有部件均假设为刚体,部件间的间隙和摩擦力忽略不计。将运动学分析结果导入VI-CarRealTime模块进行参数化处理,同时对非线性的悬架减震器阻尼特性和缓冲块刚度特性进行曲线拟合,保证仿真结果的准确性。

表1 悬架参数

图1 VI-SuspensionGen后悬架模型
用于整车动力学仿真的轮胎模型是Pacejka MF tyre5.2等式。Pacejka模型使用了由三角函数组合公式拟合轮胎特性的魔术公式,其模型公式形式相同,描述轮胎所受的力和力矩性能精确,广泛用于整车操控稳定性仿真。
此外,VI-CarRealTime中赛车的转向系统、制动系统、动力系统以及车身车架也都是参数化模型,只需要按照实车设计输入相关参数即可。参数化的整车动力学模型和道路模型可通过仿真动画反映,利于设计人员把握车辆实时动态、加快理解仿真结果。VI-Animator仿真界面如图2所示。

图2 VI-Animator仿真界面
1.2 轮胎极限载荷提取
为了计算立柱的载荷,一般取用赛车行驶时轮胎与地面接触点的作用力。由于离心力的作用,赛车过弯时会出现侧倾,其簧载质量顺势发生转移,导致外侧轮胎受力要远大于内侧。而赛车立柱又是左右对称,所以仅对单侧轮胎进行分析即可。
表2中坐标轴FX的正方向与赛车前进方向相反,FY的正方向垂直于赛车中线指向右侧车轮,FZ的正方向垂直于水平面向上。

表2 右后轮不同工况下峰值载荷 N
1.3 赛车立柱力学模型搭建
赛车前后悬架结构差异较小,所以文中以后悬架为例,根据轮胎与地面接触点的极限载荷,建立立柱的稳态力学模型[5]。
如图3为轮胎只受垂向力的作用,正视图的力学模型。其中,FZ为轮胎受到的垂向力。
由∑F=0可得
FZ+FUYsinθ1-FLZ=0
(1)
FUYcosθ1-FLY=0
(2)
以LBJ为力矩中心,建立力矩平衡方程为
FZD2-FUYcosθ1h1-FUYsinθ1h1tanθ2=0
(3)
图4为轮胎只受侧向力作用的力学模型。其中,FY为轮胎受到的侧向力。
由∑F=0可得
FLYcosθ3-FUYcosθ1-FY=0
(4)
FLYsinθ3-FUYsinθ1=0
(5)
以LBJ为力矩中心,建立力矩平衡方程为
FUYcosθ1h1+FUYsinθ1h1tanθ2-FYh2=0
(6)
式中:UBJ和LBJ为上下控制臂与立柱的铰接点,D2为点LBJ与轮胎垂直中心线的距离,h1为点UBJ与LBJ的垂直距离,h2为点LBJ与地面的垂直距离,θ1为上控制臂与水平面的夹角,θ2为主销与轮胎垂直中心线的夹角,θ3为下控制臂与水平面的夹角。
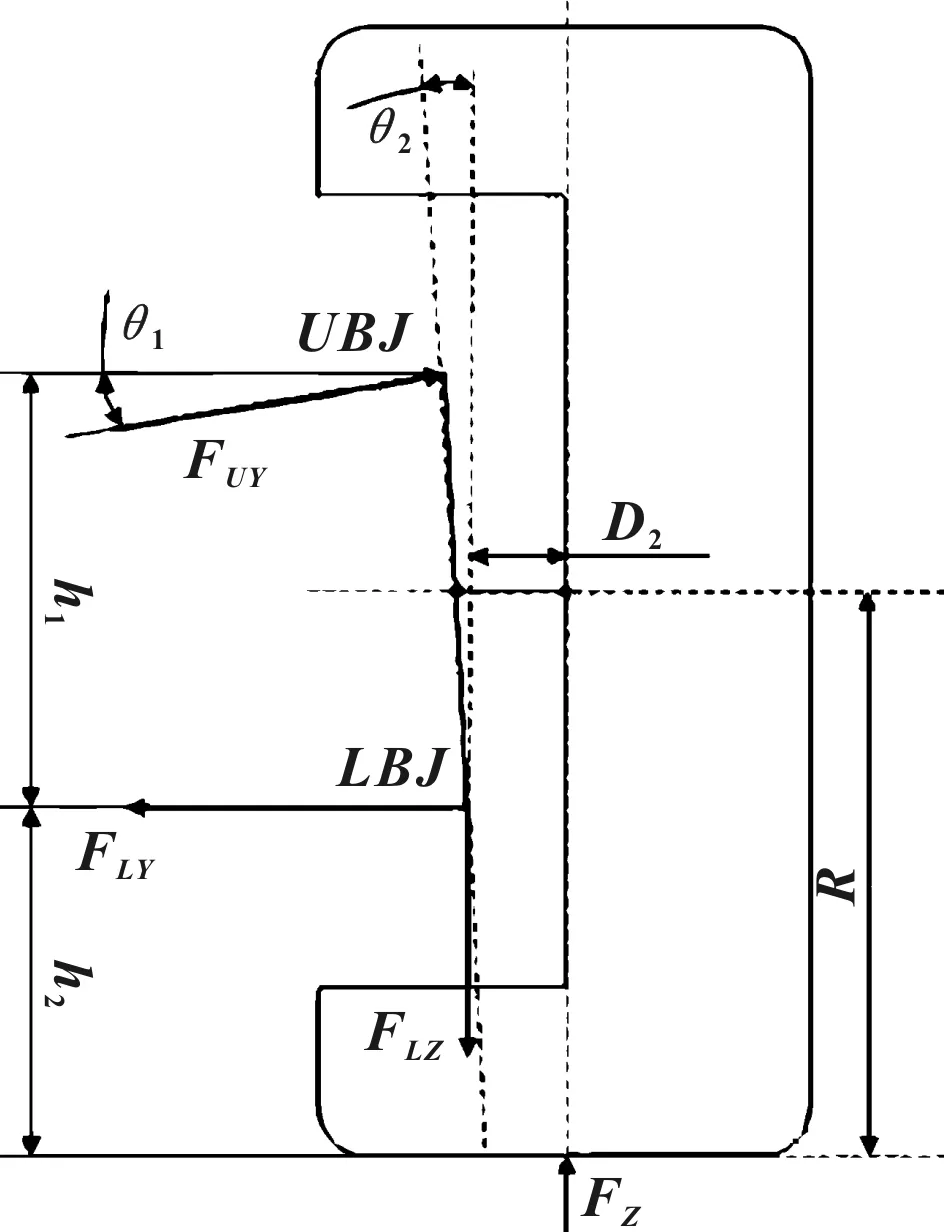
图3 轮胎仅受垂向力作用的力学模型

图4 轮胎仅受侧向力作用的力学模型
图5为轮胎仅受纵向力作用侧视图的力学模型。图中,FX为轮胎受到的纵向力,MB为制动力矩,R为轮胎半径,h3为点UBJ与轮胎水平中心线的垂直距离,α2为主销与轮胎垂直中心线的夹角。
由∑F=0可得
FLX-(FUX+FX)=0
(7)
以UBJ为力矩中心,建立力矩平衡方程
FLXh1=MB+FX(h1+h2)
(8)

图5 轮胎仅受纵向力作用的力学模型
结合上述力学模型图及公式,计算后立柱各连接点的极限载荷见表3。
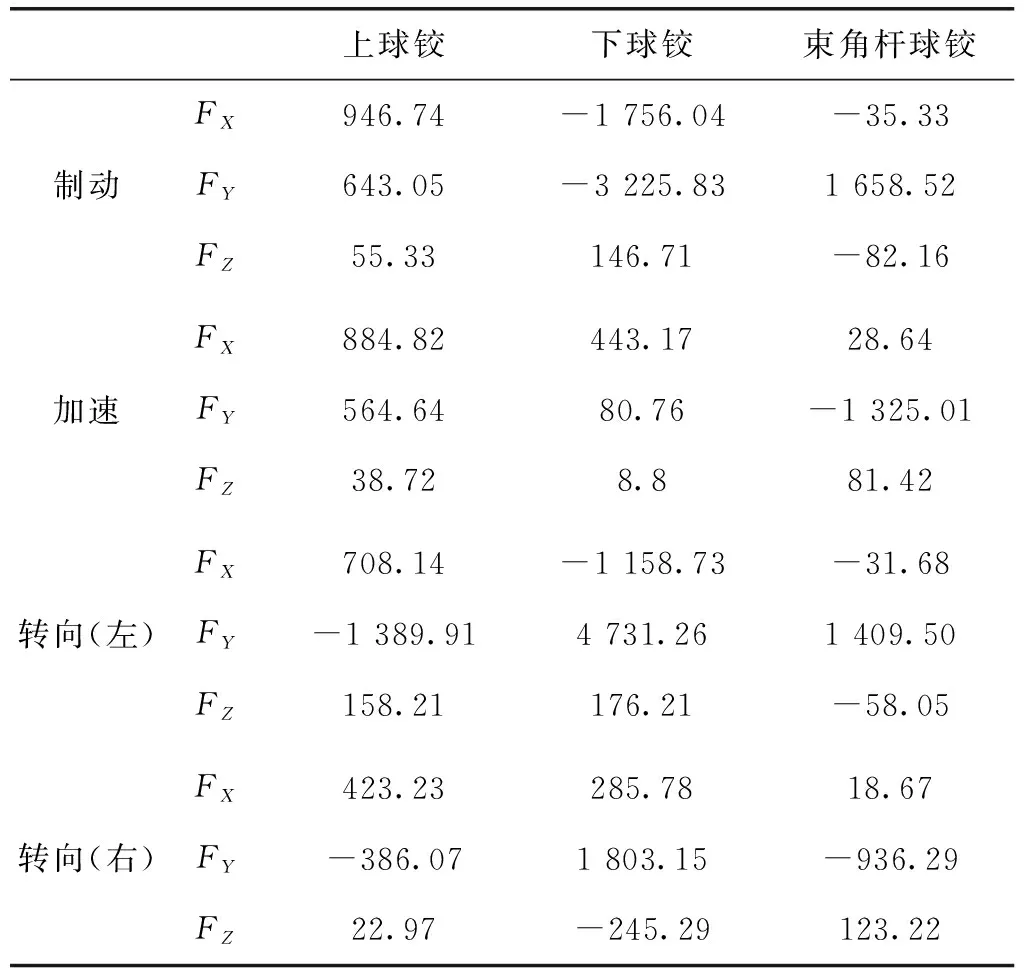
表3 后立柱连接点极限载荷 N
2 赛车立柱有限元分析
2.1 分析前处理
通过表3可知立柱下球铰受力大于上球铰,下球铰吊耳则与立柱做成一体。为方便悬架外倾角的调整,立柱上球铰可采用分体式吊耳连接。利用三维建模软件Catia建立立柱毛坯模型,再将其导入AnsysWorkbench做前处理备用。
为追求轻量化设计,FSAE赛车立柱通常采用7075铝合金作为原材料。该材料在经过人工调制后可达455MPa~520MPa的屈服强度和接近570MPa的抗拉强度,性能优于部分中低碳钢。2.81g/cm3的密度使7075铝零件的质量比同体积下钢零件要轻1/3~1/2,其他性能参数为:泊松比0.33,弹性模量72.0GPa。
2.2 拓扑优化方法
结构拓扑优化就是在预定的空间内寻求最优材料布局,同时满足最大化结构刚度的方法。当前,拓扑优化有均匀化法、变密度法、渐进结构进化法、水平集法。其中,变密度法因其程序实现容易,计算效率高而被广泛应用。由于在AnsysWorkbench中TopologyOptimization模块以变密度法为默认方法,故文中将基于变密度理论的SIMP法对新方案的立柱结构进行优化设计,其设计目标[6]如下
设计变量:
(9)
目标函数:
MinC(x)=FTU=UTKU
(10)
限制条件:
(11)
式中:E(x)为插值后材料的弹性模量;E0为实体部分材料的弹性模量;Emin为孔洞部分材料的弹性模量,由于孔洞部分移除了材料,故Emin可忽略不计;p为惩罚因子,该值越大,单元相对密度的数量越少,插值材料的弹性模量越小,p值会随着迭代次数增加;xi为单元相对密度(图6),取值在0~0.4时表示移除材料,0.4~0.6为边缘材料,0.6~1时表示保留材料,xi的区间应在可设计区内,避开载荷施加点;F为结构载荷矢量;U为结构位移矢量;K为结构整体刚度矩阵;函数MinC(x)表示在体积或质量约束下求模型的最小柔度(即最大刚度);V为优化后体积;V0为初始体积;f1为优化的体积比;M为优化后质量;M0为初始质量;f2为优化的质量比。
拓扑优化结果见表4,优化后体积为86 019 mm3,优化后质量约为242 g。
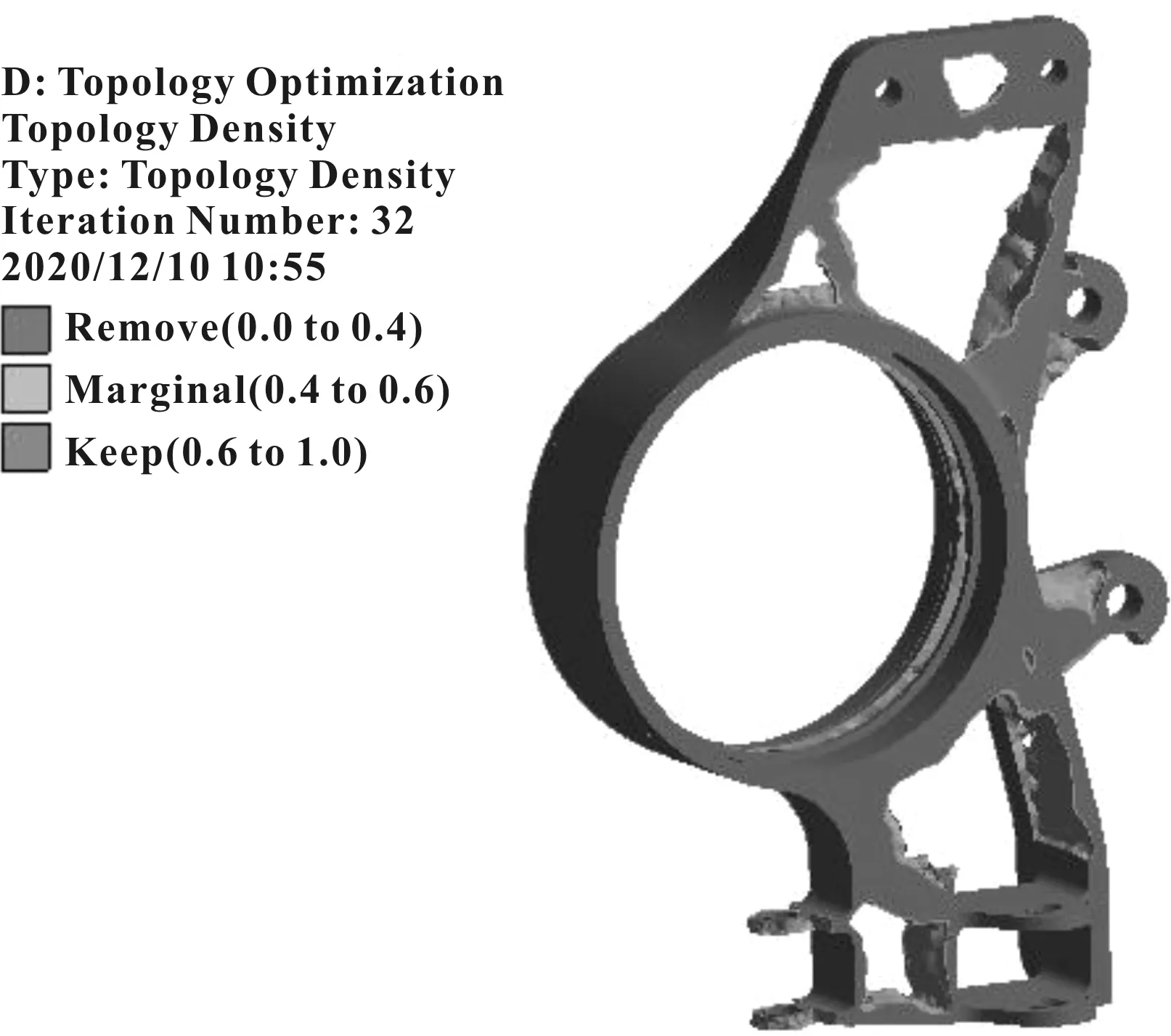
图6 拓扑优化单元密度图

表4 拓扑优化结果
为减小加工难度,实际模型需在优化结果上稍加改进,保证表面规整、平滑。
2.3 静力学校核
新旧方案极限工况等效应力图及总变形图如图7—图10所示。

图7 新方案极限工况等效应力图

图8 新方案极限工况总变形图

图9 旧方案极限工况等效应力图

图10 旧方案极限工况总变形图
由图可知,新方案最大应力为190.56 MPa,最大位移为0.453 95 mm。旧方案最大应力为373.79 MPa,最大位移为0.370 07 mm。新方案立柱质量为364 g,旧方案为382 g。虽然质量减轻幅度小,但新方案应力远小于旧方案,拥有更长的使用寿命,符合预期设计。
3 结论
文中运用车辆在环仿真软件VI-CarRealTime进行整车动力学仿真,提取赛车各极限工况下的轮胎载荷。并结合立柱力学模型,计算出Ansys静力学分析所需的边界载荷。使得新立柱在质量上进一步减轻,在力学性能上有较大提高。该设计方法还未对模型网格和疲劳仿真进行深入研究,因此有待进一步扩充[7]。
