移动重块式船舶减摇系统研究
2021-03-29杨荣武许劲松
杨荣武,许劲松,周 泉
(上海交通大学高新船舶与深海开发装备协同创新中心,上海200240)
0 引 言
船舶在风浪作用下会产生横摇,有效控制船舶横摇幅值可以改善船员的舒适性和工作条件,延长船载设备的使用寿命,提高船舶航行的安全性和经济性[1-2]。减摇装置的种类繁多,目前常用的有舭龙骨、减摇水舱、减摇鳍、移动重块、陀螺仪等不同装置,它们在减摇机理和减摇效果上存在一定的差异,需要针对性地配置控制方案,实现被动式、半主动式、或主动式控制[1-2]。
移动重块减摇系统具有机理简单、控制方便灵活的特点,可以适配大范围的船舶横摇周期,在重块质量足够大时甚至可以有效控制横倾,对于不同的工况和海况具有更强的适用性。但早期的应用尝试均受制于控制技术和机械制造技术的不完善,一直未能取得理想效果,阻碍了该类减摇系统的普及和发展。
作者针对移动重块减摇系统开展研究,根据重块移动存在极限位置和极限功率约束的特点选择模型预测控制方法MPC 构建控制器,通过动力学推导获得MPC 控制器内嵌的系统输出预测模型,成功实现了满足约束条件的最优化控制。案例船模的水池减摇试验充分验证了MPC控制器的有效性和优越性,对移动重块减摇系统的工业应用具有重要借鉴意义。
1 船舶减摇系统的原理分析
1.1 船舶减摇的动力学原理
船舶绕船长x轴方向的转动称为横摇。在波浪载荷和减摇控制力矩共同作用下,船舶横摇动力学方程可以表达为[1]
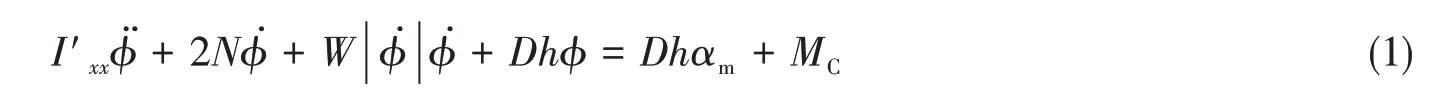
式中,总惯性矩I'xx为船体本身惯性力矩和附加惯性力矩之和,N 和W 为横摇阻尼力矩系数,D 为船舶的排水量,h为船舶的初稳性高,αm为波倾角,MC为外加的横摇控制力矩。
对于小角度横摇,非线性阻尼项可以忽略,得到以下简化方程[1]:

如果控制力矩保持MC= -Dhαm,则动力学方程右边归零,在阻尼的作用下横摇角也会衰减至零,船舶横摇被完全抑制。但在实际海浪中,由于波倾角αm随机变化,控制力矩MC难以保持和Dhαm完全一致,因此任何减摇系统都不可能完全抑制横摇角,只能追求控制力矩MC最大程度地抵消Dhαm项。而在系统设计错误或控制策略失效的情况下,控制力矩MC有可能放大Dhαm项,反而会造成船舶增摇。因此准确分析横摇控制力矩的机理对减摇系统的设计至关重要。
1.2 减摇控制力矩的机理和特点分析
根据控制力矩的产生来源不同,可以将减摇系统划分为两大类:一是以减摇水舱为代表的流体动力式;二是以移动重块为代表的机械动力式。两类系统的控制机理和性能特点均存在一定的差异性。
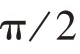
移动重块的减摇原理和减摇水舱存在相似性,通过重块移动造成左右舷的重量差异形成力矩,同时重块加速运动产生的惯性作用力也形成另一附加力矩,两者的合成力矩构成方程(2)中的控制力矩MC。相对于减摇水舱的自由液面运动,移动重块的主动控制能力更强,可以适配大范围的船舶横摇周期,在重块质量足够大时甚至可以有效控制横倾,对于不同的工况和海况具有更强的适用性。法国的Kremer[6]早在1880年就设计了第一个被动式移动重块系统,Cremieu[7]在1910年尝试了进一步的改进,1930 年前后更是出现了主动式移动重块系统,但这些尝试都没能取得满意的减摇效果。考虑到重块移动存在失控风险,加上机械装置发出大量噪声,因此长期以来移动重块减摇系统都被认为不具有发展前途。但随着现代控制技术和机械制造技术的发展,移动重块系统的既有缺陷完全可以获得有效弥补,近年的实船应用尝试已经展示了该类系统的优势[8],具备广泛应用的前景。
2 移动重块减摇控制方案
2.1 控制器的选择
根据减摇机理的分析,移动重块减摇系统必须精确控制重块的移动以保证横摇控制力矩MC最大程度地抵消Dhαm项,以获得最佳减摇效果。但是与减摇水舱不同,重块移动存在极限位置和极限功率,任何超越极限值的重块运动都会引起系统崩溃和事故风险,因此备选控制器必须具备精确处理约束条件的能力。
传统的PID 反馈控制器难以满足上述要求,无法适用于移动重块减摇系统。而现代的模型预测控制方法MPC 可以精确处理约束条件并能实现控制效果的最优性和快速性[9],避免控制不稳定并减小逆响应幅值[10-11],是移动重块减摇系统的理想控制器。
MPC 控制算法的基本原理可通过图1 所示的单输入-单输出模型加以说明[9]。对于当前时刻k,r(t|k)为系统未来时域P 内的输出目标序列,u(t|k)为任意的未来输入序列。根据内嵌的系统输出预测模型可以预报出对应于r(t|k)的输出序列y(t|k)。MPC 控制算法可以在当前时刻k 寻找到最优的未来输入序列u(t|k),使得y(t|k)与目标序列r(t|k)的偏差最小,此时最优输入序列的第一项u(k|k)成为当前时刻的最佳控制信号。系统输入和输出的限制条件可以在上述寻求最佳的过程中精确考虑,这是其它控制算法所不具备的特别功能。

图1 MPC控制算法基本原理[9]Fig.1 Basic principle of MPC[9]
与常规的PID 控制器相比,MPC 控制器所具有的精准控制优势相当程度上来源于内嵌的系统输出预测模型,而大多数系统输出预测模型难以做到完全准确,均存在一定程度的简化和近似。MPC 控制器中已经隐含了适应这种模型近似性的健壮算法,即在当前时刻k 寻找到的最优未来输入序列u(t|k)中只选取第一项u(k|k)成为当前时刻的最佳控制信号,其它输入序列项全部舍弃。这样可以最大限度利用各个时刻的滚动优化过程进行修正,有效避免了误差累积。
2.2 减摇控制力矩的推导
移动重块减摇系统的常规布置如图2 所示[12],重物导轨一般对称于船舶的中线面水平放置,重物在执行机构带动下沿导轨运动,重块重心距船舶重心的垂向距离为zm。
由于本文只考虑横摇问题,可以将多自由度耦合运动简化成如图3 所示的单自由度横摇模型[13],图中d(t)为重块的位置变量,F 为执行机构施加给重块的推力,ϕ 为船舶横摇角度。根据受力分析,船舶受到的减摇控制力矩Mc可以表达成[13]:


上述减摇控制力矩的推导过程实际隐含了如下运动假设[13]:一是船舶做直线匀速运动,二是纵摇和升沉运动被完全约束。因此表达式(3)是一个简化近似结果,存在一定的不精确性。
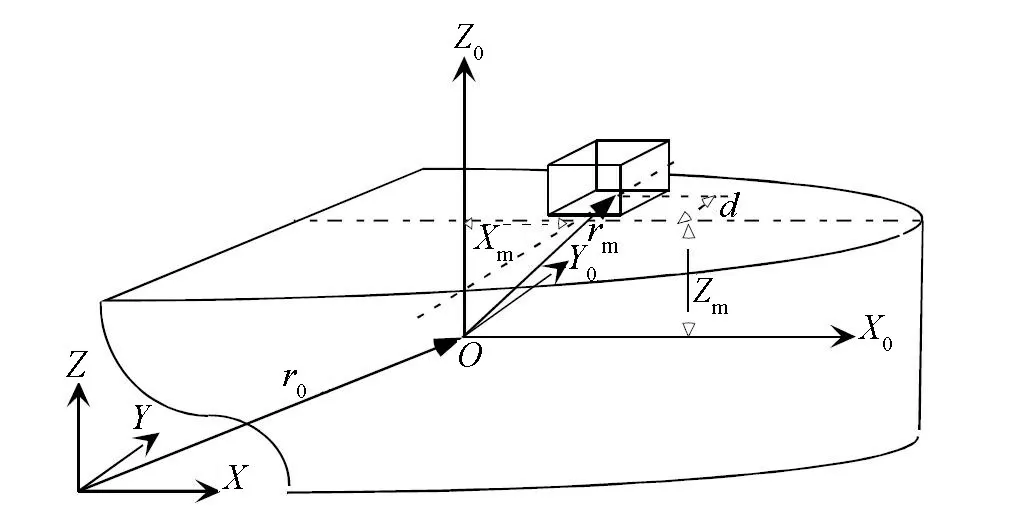
图2 移动重块系统示意图[12]Fig.2 Illustration of the moving mass system[12]
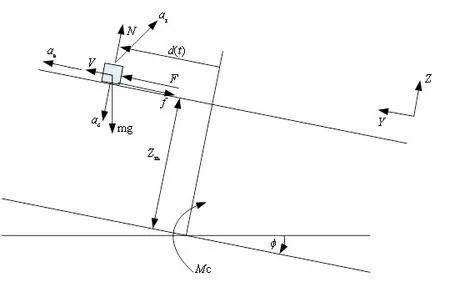
图3 移动重块系统受力分析图[13]Fig.3 Force analysis of the moving mass system[13]
2.3 MPC控制器的构建
由于MPC 控制器必须包含一个内嵌的系统输出预测模型,因此在控制器构建过程中首先需要推导出重块移动位置与减摇控制力矩之间的传递函数模型。
对于一个正常运行的移动重块减摇系统,可以假定减摇装置开启后维持小幅横摇,因此sinϕ ≈ϕ,cosϕ ≈1,同时d(t)的二次项可忽略。根据式(2)和式(3),使用框图法利用Mason 增益公式得到如下传递函数[13]:
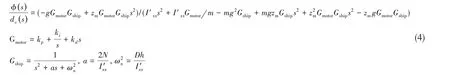
式中,Gmotor是电机的传递函数,Gship是船舶横摇的传递函数,m 是重块的质量,I′xx是船舶的总惯量,kp、ki、kd是电机PID的参数,a是线性阻尼系数,N是线性阻尼力矩系数,ωn是船舶的固有横摇频率。


式中,Wϕ和WΔd分别为权重矩阵。根据传递函数(4),上述最优化问题的目标函数和约束条件都可以表达成控制序列Δd 的函数,形成标准形式的二次规划问题,通过QPKWIK 算法[14]获得最优输入系列d(t|k),其中第一项d(k|k)即为当前时刻k 的最佳控制值。系统输入和输出的限制条件在上述求解过程中自然满足,这是其它控制算法所不具备的特别功能,非常符合移动重块减摇系统的安全性要求。
3 船舶减摇的模型试验方法
3.1 试验案例船
船舶减摇试验采用某型科考船的缩尺船模作为案例船[15],船模总长为4.08 m,型宽为0.73 m,吃水为0.23 m,排水量为546 kg,在静水中的横摇固有周期为2.05 s。船模处于零速横浪状态,在甲板同一位置分别安装移动重块系统和自由面减摇水舱进行减摇对比试验,安装平面距基线高度为0.68 m。船模横摇角由姿态仪AHRS测量,波高采用浪高仪测量,数据以50 Hz频率采样并记录。
3.2 移动重块减摇试验
移动重块减摇试验的整体布置如图4所示,重块导轨对称于船舶的中线面水平放置,移动重块质量为6.07 kg,在电机和齿轮的带动下可以沿导轨运动,移动重块的位移范围限制为-0.35~0.35 m。完整的移动重块闭环控制框架如图5 所示,重块位置的控制指令由运行在拖车计算机上的MPC 控制器实时给出。

图4 移动重块减摇试验布置Fig.4 Anti-rolling test arrangement of moving mass system
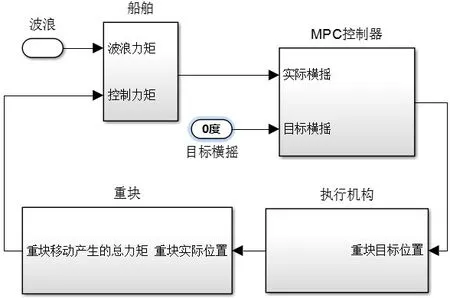
图5 移动重块减摇试验的控制框架Fig.5 Control framework of moving mass system
3.3 减摇水舱试验
为验证移动重块减摇系统的应用效果,对比试验采用自由面减摇水舱,水舱的固有频率由舱内水位决定。该矩形水舱沿船宽方向的尺度为0.73 m,高度为0.108 m,沿船长方向的尺度为0.25 m,舱内水位为0.054 m,水体总重为14.4 kg,整体布置如图6 所示。此时水舱的固有频率与船舶谐摇频率一致,水舱中自由液面流动产生的动力矩与液位差产生的静力矩合成减摇总力矩,比横摇相位滞后90°,处于减摇效果最佳状态。

图6 减摇水舱试验布置Fig.6 Anti-rolling test of free surface tank
4 船舶减摇试验结果
船模在不配置减摇设备、配置移动重块减摇系统、配置自由面减摇水舱三种状态下分别进行了系列规则波试验,获得了如图7所示的RAO响应曲线。
船模在同样的三种减摇配置下完成了两组JONSWAP非规则波试验,波谱参数详见表1,横摇试验结果列于表2。

图7 配置不同减摇装置的横摇RAO曲线Fig.7 Roll RAO curves with different anti-rolling devices

表1 试验用JONSWAP波谱参数Tab.1 Parameters of the JONSWAP waves
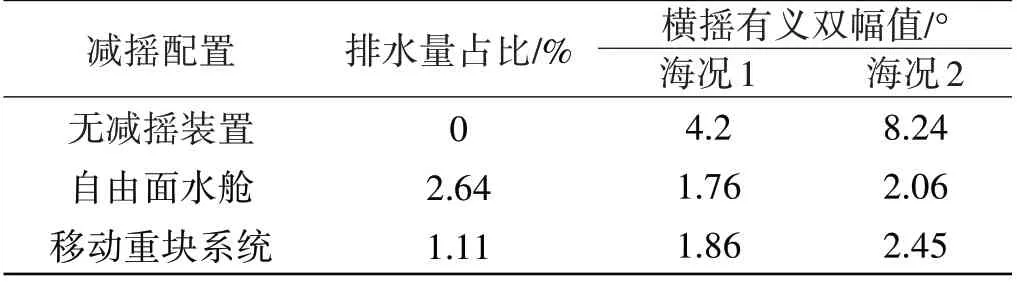
表2 非规则波中的减摇效果Tab.2 Anti-rolling effects in irregular waves
试验中移动重块的启动时刻设置为第160 s,移动重块系统在海况1中的减摇时历曲线、重块位移时历曲线、驱动功率时历曲线分别如图8、图9 和图10 所示;在海况2 中的减摇时历曲线、重块位移时历曲线、驱动功率时历曲线分别见图11、图12和图13。从时历记录中可以看出,移动重块的位移范围没有超出-0.2~0.2 m,重块移动速度没有超过0.7 m/s,电机的最大驱动功率没有超过6 W。

图8 海况1中移动重物的减摇时历曲线Fig.8 Rolling time history of moving mass in Wave State 1

图9 海况1中移动重块的位移时历曲线Fig.9 Displacement time history of moving mass in Wave State 1
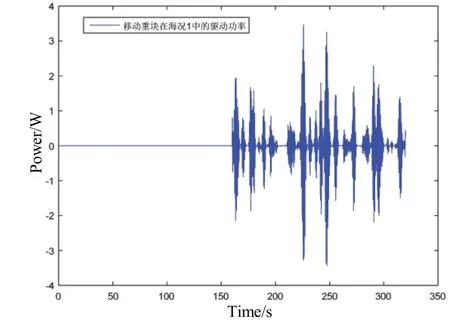
图10 海况1中移动重块的驱动功率时历曲线Fig.10 Driving power time history of moving mass in Wave State 1

图11 海况2中移动重物的减摇时历曲线Fig.11 Rolling time history of moving mass in Wave State 2

图12 海况2中移动重块的位移时历曲线Fig.12 Displacement time history of moving mass in Wave State 2

图13 海况2中移动重块的驱动功率时历曲线Fig.13 Driving power time history of moving mass in Wave State 2
5 结 论
本项研究成功构建了移动重块减摇系统的MPC控制器,并以某型科考船的缩尺船模为样船,完成了不同减摇装置的对比试验,得到了以下结论:
(1)移动重块减摇系统在重块质量的排水量占比显著小于减摇水舱的条件下,可以获得与自由面减摇水舱相当的减摇效果,这对于排水量裕度紧张的船舶极具价值;
(2)相对于减摇水舱的自由液面运动,移动重块的主动控制能力更强,几乎可以适配任何船舶横摇周期,在重块质量足够大时甚至可以有效控制横倾,对于不同的工况和海况具有更强的适用性;
(3)模型预测控制方法MPC可以精确处理约束条件并能实现控制效果的最优性和快速性,避免控制不稳定并减小逆响应幅值,在保证减摇效果和系统稳定性的同时有效保护了执行机构,是移动重块减摇系统的理想控制器。
