跨临界二氧化碳热泵系统动态性能的仿真研究

2021-03-29张永明陈振乾

建筑热能通风空调 2021年2期

张永明陈振乾

东南大学能源与环境学院

能源不仅是社会发展的基本动力、现代经济的重要支撑，同时也是人类文明进步的主导因素。目前广泛使用的人工合成制冷剂都具有相对较高的 ODP（臭氧消耗潜能值）或 GWP（全球变暖潜能值），因此采用如 CO2等自然工质作为制冷剂又逐渐成为人们研究的热点，再次得到人们的重视。目前对于二氧化碳制冷系统的仿真主要集中在制冷空调领域[1-3]，且多为稳态模型或是分相模型[4]。为了更进一步研究二氧化碳在热泵热水系统中的动态性能，本文在实验的基础上建立了跨临界 CO2热泵热水系统的分布式动态仿真模型，通过实验进行了模型验证并利用该模型分析了CO2热泵热水系统的一些动态特性。

1 二氧化碳热泵热水机组模型

二氧化碳热泵热水系统采用跨临界循环，系统模型的组成见图1，主要包括气冷器、蒸发器、压缩机、膨胀阀等部件。二氧化碳通过压缩机压缩成高压高温气体后进入气冷器与水换热过冷，流经膨胀阀节流降压后进入蒸发器内相变吸热，通过汽液分离器的饱和蒸汽重新进入压缩机压缩，完成循环。其中，压缩机与膨胀阀的热惯性较小，状态参数变化速度较快，结合实测数据利用效率公式建立其准稳态数学模型。对气冷器和蒸发器建立分布参数模型并设计相应算法。通过质量守恒，动量守恒和能量守恒将各部件相耦合，得到可以描述系统动态特性的仿真模型。

图1 跨临界CO2热泵循环系统示意图

1.1 气冷器模型

在二氧化碳跨临界热泵系统中，冷凝器被称为气体冷却器。气冷器中 CO2的放热过程位于超临界区，换热为自身显热，整个换热段均处于单相区。本文采用的气冷器为全逆流壳管式换热器，内管为紫铜管。通过确定进出口边界条件进行分布式计算，微元段示意图如图2 所示。

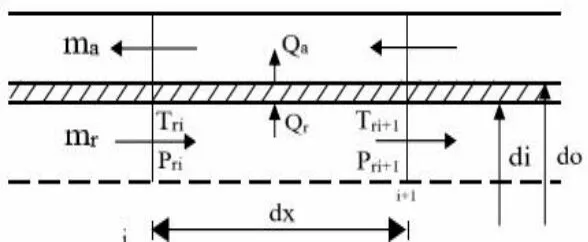
图2 气冷器模型

为便于计算与讨论，模型假设：

1）气冷器简化为一水平细长管，制冷剂做一维轴向流动，忽略制冷剂的轴向导热。

2）微元段内各处制冷剂压力相等，即忽略由制冷剂动量变化和摩擦引起的轴向压降。

3）忽略管壁的轴向导热，并视外管为绝热。

4）忽略水侧压降。

气冷器控制方程：

式（1）～（ 6）分别为气冷器微元段处制冷剂侧质量守恒方程，制冷剂侧能量守恒方程，水侧能量方程，管壁侧能量守恒方程以及制冷剂侧换热方程和空气侧换热方程。把式（1）、（5）、（6）代入式（2）、（3）、（4）用一阶精度向后差分离散能量方程，并将出口项置于等式左侧：

1.2 蒸发器模型

不同于气冷器中制冷剂始终处于超临界无相态变化，蒸发器中 CO2的吸热过程位于亚临界区，假设蒸发器入口处制冷剂处于两相区，出口处制冷剂处于过热区。计算两相区状态参数时需要引入空泡系数理论[5]；对于运行在析湿工况下的换热器，由于湿空气在换热过程中存在传质传热现象，物性参数不断发生变化。故有必要考虑析湿工况下的换热情况。本文采用的蒸发器为百叶窗式翅片管换热器，内管材质为紫铜管，翅片材质为亲水铝箔。蒸发器微元段示意图如图3所示。

为便于计算与讨论，模型假设：

1）蒸发器简化为一水平逆流换热管，制冷剂做一维轴向流动，忽略制冷剂轴向导热。

2）在两相区域，汽相和液相制冷剂处于热力平衡状态。

3）微元段内各处制冷剂压力相等，即忽略由制冷剂动量变化和摩擦引起的轴向压降。

4）忽略管壁的轴向导热，忽略翅片间相互导热。

5）忽略空气侧压降。

蒸发器控制方程：

上述方程组中ξ为析湿系数，用以描述在湿工况换热时总放热量与显热热量的比值。湿空气的物性参数计算见文献[6]。当制冷剂处于两相区换热时，状态参数密度ρ通过空泡系数法计算。蒸发器离散过程与气冷器类似，此处不再赘述。

1.3 压缩机模型

压缩机是二氧化碳热泵热水机组的最重要的部件，压缩机的运行工况直接关系到循环压力及制冷剂流量，从而影响制热量和性能系数。本文仿真的侧重点在于系统各部件的耦合关系及变工况下系统状态参数的响应规律而非压缩机的实际工作过程，且压缩机的动态响应较换热器部件快得多，故综合各方面考虑，利用效率法对压缩机进行准稳态模型的建立。

为便于计算与讨论，模型假设：

1）压缩机体积较小，而且置于几乎密闭的压缩机室中，因此可将其压缩看作是一绝热过程。

2）压缩机转速较快，吸气，压缩和排气过程都在很短的时间内完成，故可认为压缩机处于准稳态。

压缩机热力学参数主要包括制冷剂质量流量、输入功率、出口比焓等。通过确定压缩机进出口压力，可以描述其出口状态，具体关系如下：

式中：ηv为容积效率，反映压缩机实际排量与理论排量的比值；ηis为等熵效率，反映压缩机实际耗功与理论等熵压缩时耗功的比值，即压缩过程偏离等熵过程的多寡。

目前已有文献[7-9]对于容积效率和等熵效率大多采用实验数据的拟合得到经验公式，本文采用的压缩机为松下公司生产的CO2双转子压缩机。为了更加准确地描述压缩机的性能，以厂家所提供的压缩机性能曲线为依据，并参考 Tagliafico[10]等人所拟合的关联式形式，得出适用于本仿真的压缩机容积效率和等熵效率的关联式：

1.4 电子膨胀阀模型

电子膨胀阀通过调节阀门开度实现制冷剂流量的调节从而实现蒸发器出口制冷剂过热度控制。由于制冷剂经流电子膨胀阀时间很短，可近似看作为等焓节流过程。与压缩机相似，本文对膨胀阀采用准稳态模型建模，假设流体在膨胀阀中等焓流动，质量流量可通过式（21）、（22）计算：

1.5 换热关联式与压降模型

跨临界 CO2热泵系统主要包含制冷剂在气冷器内的超临界强迫对流换热以及在蒸发器内两相区的亚临界对流沸腾换热和过热区的单相强迫对流换热。近年来各国学者对 CO2的换热展开了许多研究[11-14]并总结出适用于不同管径和雷诺数的换热关联式，本文结合机组的实际情况及文献[15]对于已有换热关联式的误差分析总结选取最适合的换热关联式。

对于蒸发器两相区制冷剂采用 Cheng（2006）[16]换热关联式。蒸发器过热区和气冷器制冷剂采用Gnielinski 换热关联式。气冷器水侧采用 Dittus-Boelter换热关联式。蒸发器空气侧采用 C.C.Wang[17-18]换热关联式。

制冷剂在流经换热管时产生压力损失，为使各部件的压力达到平衡，需要插入压降模型来反映真实的动态运行特性。对单相流动流体的压力损失，采用压降关联式：

其中，摩擦因子f由Blasius 关系式求得。

对处于两相区流动的制冷剂，压降主要由摩擦压力梯度和动量压力梯度两部分组成：

式（25）具体计算见文献[19]。

1.6 系统模型及求解

将建立完毕的各部件模型根据质能守恒以及压力平衡进行耦合即可得到完整的二氧化碳热泵系统动态模型。压缩机输入参数为吸气压力和温度。输出参数为制冷剂质量流量和压缩机耗功。换热器输入参数为制冷剂进口温度，压力以及质量流量，进水温度，质量流量。输出参数为制冷剂出口温度，压力和出水温度。膨胀阀输入参数为制冷剂进口焓值和压力。输出参数为出口焓值和制冷剂质量流量。以压缩机作为起点，通过假设吸气压力和排气压力进行迭代计算，前一个部件的输出参数为后一个部件的输入参数。系统动态仿真流程见图4。

图4 跨临界CO2热泵热水系统动态仿真流程图

2 仿真结果及分析

2.1 模拟结果与试验数据的比较

本文所模拟对象中所采用压缩机为为双转子变频压缩机，转速范围 37～120 r/s，通过变频器控制其转速。气冷器为套管式换热器，外管内径16 mm，内管内径9.7 mm，总长19.2 m。蒸发器为翅片式换热器，管外径4.2 mm，壁厚4 mm，空气流动方向上布置24 排管，排列方式为叉排。节流装置为电子膨胀阀。

为验证所建立系统动态模型的正确性，于某实际CO2热泵系统性能试验台进行动态试验并于模拟结果进行比对，实验工况如表1 所示。

表1 实验工况

图5 所示为所处实验工况下该实际 CO2热泵系统从停机到启动到最终稳定时机组关键运行参数的动态比较。从开机过程中可以看出，系统压力从启动到稳定时低压侧和高压侧保持持续变化（约 100s 稳定），排气温度及出口水温随时间的变化较压力变化相对较慢（约200s 稳定），模拟参数的变化趋势与实际情况基本一致。计算值与实验值存在一定偏差，造成这一现象的原因主要是因忽略了压缩机和膨胀阀的动态特性而假定两者为准稳态所致。

图5 热泵系统主要性能参数的动态响应

表2 稳态参数对比

表2 展示了系统运行至稳定后一些关键运行参数的模拟结果与实验数据的比较，可以看到相对误差基本保持在 10%以内，其中蒸发器进口温度相对误差最高，但绝对温差不超过3 ℃。综上所述，该模型能够较好反映真实系统的动态运行过程，可用于指导跨临界CO2热泵系统的系统控制与优化设计中以节约成本。

2.2 系统变工况特性

当系统达到稳态运行后受到外界扰动或主动改变控制参数，都会对系统运行性能产生影响。本文所建立的所建立的跨临界 CO2热泵热水系统可以描述当压缩机转速，电子膨胀阀开度及进口水量等参数阶跃变化时系统的动态响应，亦可预测多个控制参数变化下整体的动态特性。通过向模型添加扰动，观察并研究控制参数变化下系统动态运行特性，为系统零部件和控制方案的优化设计打下良好基础。

图6 为改变压缩机转速从90 r/s 到 70 r/s 或110 r/s 时系统各性能参数的变化曲线。图 7 为改变进水流量从 0.032 kg/s 到 0.025 kg/s 或0.048 kg/s 时系统各性能参数的变化曲线。

图6 性能参数随压缩机转速变化的动态响应

图7 性能参数随水侧流量变化的动态响应

当压缩机转速从90 r/s 提升至 110 r/s，系统高压侧压力迅速上升至9.6 MPa，低压侧压力亦降至 2.58 MPa。制冷剂质量流量从0.0246 kg/s 增至0.0278 kg/s，响应过程约为20s 左右。而换热器热惯性较大，随系统排气温度升高，热水温度上升至 65.37 ℃，响应过程约为 140 s 左右。当进水流量从 0.032 kg/s 减小至 0.025 kg/s 时，系统各性能参数变化方向与增大压缩机转速相同，但增速有较明显区别。高压侧压力，低压侧压力以及制冷剂质量流量重新达到稳态约耗时90 s，这是由于在各参数相互耦合的动态系统中，进水流量的变化首先影响气冷器内的换热并间接影响压缩机的运行工况，故动态响应较慢。