基于主成分分析与模式匹配的空调箱故障检测

晏新奇 杨学宾 何如如

东华大学环境科学与工程学院

0 引言

预计从 2015 年到 2030 年，中国的能源需求将增长4.5%[1]，其中建筑系统的能源消耗通常占总能耗的40%～50%[2]。然而，随着空调系统变得日益复杂，空气处理机在维护不当时，许多故障仅通过人为观察或判断难以被及时发现，导致空调系统的能耗通常比正常运行时增加15%～30%[3]。因此，开发与完善空调系统的故障检测技术十分有必要。

近年来，故障诊断技术得到了飞速的发展，国内外许多学者进行了大量的科学研究工作。Padilla Miguel 等[4]提出了一种结合主成分分析法与主动功能测试的方法，能够有效隔离空调箱故障。Timothy Mulumb 等[5]对将支持向量机技术应用于在线估计器递归计算模型参数，提出了一种基于模型的故障诊断方法。王海涛等[6]提出了残差累积和控制图结合规则的方法。Rui Yan 等[7]提出了一种基于决策树的空调箱数据驱动诊断策略，采用分类回归树算法进行决策树归纳。Y ang Zhao 等[8]提出了一种诊断贝叶斯网络为基础的方法来诊断大多数常见的空调箱（Air Handling Unit，AHU）28 个故障。D ebashis Dey 等[9]提出将空调箱性能评价规则与贝叶斯信念网络相结合，开发了一种AHU 故障检测与诊断方法。本文采用ASHREA 1312现场实测数据，结合主成分分析（Principal Components Ananlysis，PCA）与模式匹配（Patten Matching，PM）方法检测故障。

1 建模数据库介绍

1.1 系统介绍

本文验证数据来自美国爱荷华州能源站[10]现场实测的数据。该建筑物东南西北方向各有并排的测试房间A 和 B，面积相同并且彼此相邻。房间A 内引入故障，房间B 作为参考房间，保持正常运行。图 1 为空气处理与控制原理图。

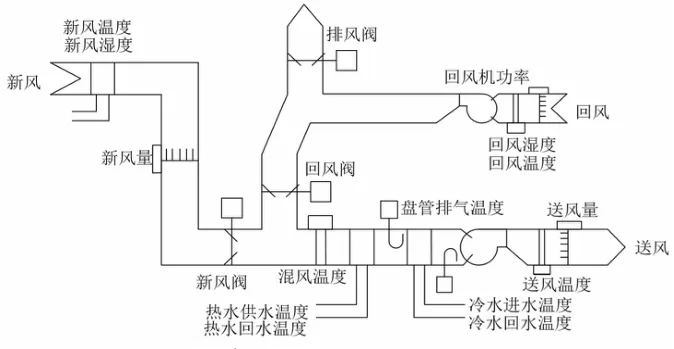
图1 空气处理与控制原理图

1.2 数据采集

冬季现场实测的新风阀，热水盘管，水阀的故障数据和3 天正常运行数据。故障描述见表1 所示，每天记录24 h，采样时间间隔为1 min。

表1 故障描述

现场实测时，通常在上午 6:00 后通过人为操作引入故障。

2 主成分分析法

主成分分析又称主元分析法，被用于数据压缩和信息提取。在保证尽可能多的原始变量信息的条件下达到降维目的，重新构造出能够表达原始变量的综合指标。

2.1 PCA 基本理论

主成分分析方法的基本原理即通过正交变换，将分量相关的原随机变量转换成分量不相关的新变量。将测量数据空间分解成为两个正交的子空间，分别为主成分子空间和残差子空间。

2.1.1 主成分分析法建模过程

根据参考文献，主元分析法的建模过程可以概况为以下几个步骤[11]：

①原始数据的预处理：对原始数据进行筛选以及标准化处理。

②计算变量的协方差矩阵。

③对协方差矩阵进行特征分解，求得特征值及特征值所对应的单位特征向量矩阵。

④确定最优主成分数l。

⑤计算投影矩阵。

2.1.2 故障检测依据

当某一故障发生后，测量数据在残差子空间内的投影会急剧增加，由此可判断是否发生故障。通常采用平方预测误差（squared prediction error，SPE）即Q统计量来衡量，如式（1）所示。

式中：P为特征值所对应的单位特征向量矩阵。

计算出正常运行数据的SPE指标值为判定指标，用δ表示；δ值计算方法如式（2）：

当Q≥δ时，说明系统发生故障；当Q＜δ时，说明系统未发生故障。

2.2 数据筛选

在冬季6:00 至18:00 空调运行期间，考虑到办公建筑空调系统根据上下班时间启停运行，中午是室内人员负荷会发生变化的休息时段，所以未使用这个不稳定时间段的数据进行故障检测。

为表示空调系统的运行特性，基于热平衡模型，为建立 PCA 模型选取 12 个变量：①新风量、② 送风量、③回风量、④ 新风温度、⑤ 混合风温度、⑥ 送风温度、⑦回风温度、⑧ 送风湿度、⑨ 回风湿度、⑩ 冷水供水温度、冷水回水温度混合水温度。这 12 个变量对系统的能耗及室内舒适度均有较大影响。

3 模式匹配原理

模式匹配方法在检测故障中可用于定位合适无故障运行历史的数据库[12]。当空气处理机组在类似的气候条件和内部负荷下运行时，其运行测量值规律也类似。因此，用相似性系数来定位与当前数据（Snap data，下文简称 S）具有相似运行条件的历史数据（Historical dat a，下文简称H）。

3.1 相似系数法

Krzanowski[13]开发了一种通过PCA相似因子SPCA量化两个数据集相似性的方法。为每个数据集分别建立PCA模型，相应的PCA模型有l个主成分，两个数据集S和H的间PCA相似系数为:

S PCA∈[0,1]，其值愈接近1，表示相似程度愈大，愈接近0 表明相似程度越小。

3.2 气象及负荷数据

当空调箱在类似的气候条件和负荷条件下运行时，过程变量（如送风流量，风阀和水阀等参数变化）也类似。因此对历史数据进行初步筛选，以确定与当前运行条件类似的时间段。

表2 的组合 1 中列出了表示天气和房间负荷条件的可选定传感器，然而，这些传感器甚少用于一般建筑物。在这种情况下，考虑组合2。

表2 气候及运行参数常用传感器

3.3 候选池与滑动窗口

3.3.1 数据候选池

为选取与实时数据气象及负荷条件最相似的无故障历史运行数据，将正常运行的历史数据分割成长度为 60min 的数据窗口，当前数据窗口与历史数据窗口具有相同维度。分别计算当前数据窗口与每个历史数据窗口气候条件参数（表2）的相似系数。将相似系数最高的5 个历史数据窗口组合纳入候选池，供后续分析使用。

3.3.2 滑动窗口

为了定位历史数据库中不同起始点的现象，采用滑动窗口。本文中，窗口大小a取60 min。通过调整窗口在历史数据中移动的速度可影响模式匹配的准确性，滑动速率w为当前数据窗口长度的十分之一到五分之一[14]，为使得结果更加精确，选取为5 min。

图2 滑动窗口原理示意图

4 PCA-PM 模型验证

4.1 PCA-PM 流程

利用无故障历史运行数据训练的PCA模型，计算系统实时监测运行数据的SPE值。故障检测率指正确检测到的故障数与故障总数之比[15]，在本研究中即是一段时间内超出δ值的时间占所选时间段的比例。若故障检测率大于70%，则该时间段被定义为有故障。若故障检测率在40%～70%，则定义为疑似故障。检测率若小于40%，则为无故障。空调的各项数值作为测试数据，代入模型中进行计算。图 3 为PM-PCA 原理流程图。

图3 PM-PCA 原理流程图

4.2 无故障测试

无故障检测结果见图4～6，分别在三个无故障日中选择每日8:00-9:00 的数据进行检测。这三天的故障检测率分别为 26.7%、28.3%、25%，未检测出故障，即无误诊断情况，结果正确。

图4 无故障主成分分析变量统计图1

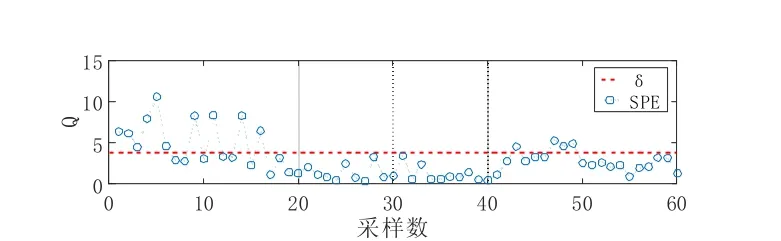
图5 无故障主成分分析变量统计图2

图6 无故障主成分分析变量统计图3

4.3 故障测试

4.3.1 热水盘管结垢

热水盘管结垢时候，热水盘管换热量大量减少，系统的热量不足以处理室外新风到所需状态，引发系统风侧及水侧均有异常。由图7 和图8 可以得出，二者的故障检测率分别为86.7%和100%，均判断为故障，检测结果正确。热水盘管结垢程度大的故障（图 8）检测出的SPE值比图 7 大，且检测率更高，说明该检测模型能够反映出热水盘管结垢故障的程度。

图7 热水盘管结垢程度小的故障主成分分析变量统计图

图8 热水盘管结垢程度大的故障主成分分析变量统计图

4.3.2 热水流量减少

如图 9～11 所示，热水流量依次减少，热水流量的增减直接影响到系统的供热量，系统得不到所需热量导致各项参数异常。图 9、图 10分别反映热水流量轻度和中度减少的统计图，故障检测率分别为78.3%和75%，较为接近。图 11 表示热水流量重度减少，其故障检测率为88.3%，明显大于前二者，说明该故障发生时，PM-PCA 模型能够正确检测出故障并反映故障程度，但当热水流量减少量程度太小时，故障程度不能很好的体现。

图9 热水流量轻度减少的主成分分析变量统计图

图10 热水流量中度减少的主成分分析变量统计图

图11 热水流量重度减少的主成分分析变量统计图

4.3.3 冷水阀卡住

通常情况下，冬季冷水阀开度为 0，如图 12 所示，在冷水盘管阀卡在 100%情况下，为保持送风温度，热水盘管会在 100%开度下运行。但由于冷水阀开度过大，冷量不能完全被抵消，还是会造成系统紊乱，送风温度会明显低于正常值，热水盘管供水温度和流量将有明显升高。当冷水阀卡在 20%时，故障检测率为63.3%，虽不高于70%，可判断为疑似故障。这是由于当冷水阀卡在较低阀位时，可调节热水阀位，增大热水流量以保证送风温度，使系统接近正常运行。因此该故障对系统整体影响相对不大，故障检测率较低。冷水阀卡在全开的检测率 85%，明显高于卡在 20%开时的检测率 63.3%（图 13）。故障检测结果正确，且能够反映出故障程度。

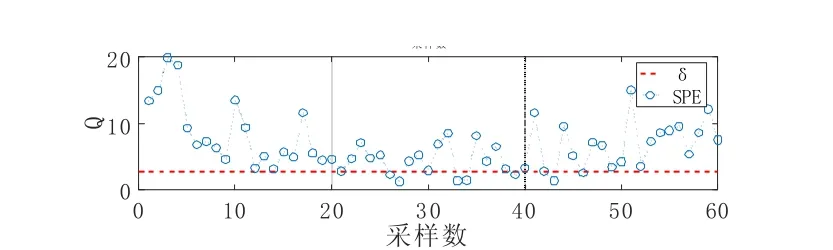
图12 冷水阀卡在100%开的主成分分析变量统计图

图13 冷水阀卡在20%开的主成分分析变量统计图

4.3.4 新风阀卡住

冬季工况下，本系统正常运行时新风阀开度保持在40%。新风量减小会导致混合风温度增大，处理新风所需的热量降低，回水温度随之升高等影响，给系统参数带来较大变动。当卡在较高阀位时，新风量增大，以上参数变化趋势与卡在低位时相反。检测结果如图14、图 15 所示，当新风阀卡在全关时，模型的SPE 值处于0～30 之间，故障检测率为85%。而当其卡在 52%时，故障检测率为 75%，SPE 值处于 0～15 之间，低于图14 的检测结果。因此检测结果正确，且能够反映出故障程度。

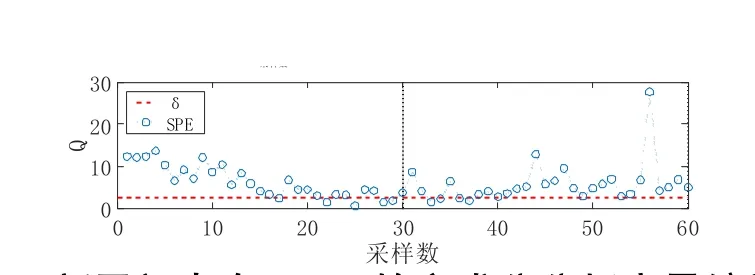
图14 新风阀卡在0%开的主成分分析变量统计图

图15 新风阀卡在52%开的主成分分析变量统计图

4.4 故障检测结果

故障检测结果汇总如表 3所示，由表中结果可看出，PM-PCA模型能够有效检测出故障，且同种故障的程度越大，检测率越高。

表3 故障检测结果

5 结论

本文提出了一种基于天气条件模式匹配和 PCA的系统级故障检测方法。利用室外空气焓等相似气象条件，寻找并提取无故障历史数据库，选择 PCA 模型中故障检测的关键变量并检测不同故障，以 AHRAE 1312 的数据为依托，在 4 个冬季常见的故障得到成功验证。本文只选取寒冷的冬季工况进行研究，无论哪个气候工况，都应选择相同季节工况下的正常数据建立PCA 训练模型进行训练。本文主要得到以下结论：

1）测试实例表明，该方法能够有效地检测出 AHU故障，是一个有效的、低成本的检测方案，适用于各种各样的暖通空调系统。

2）该模型根据Q值反映出故障程度，当故障程度越大时，故障检测率也越高，且Q偏离δ阈值的程度也会越大。说明故障程度越大，检测效果越好。

3）通过使用滑动窗口模型，有助于系统在较短时间内及时检测出异常。