配筋UHPC柱的抗震性能及影响因素分析
2021-03-29邓宗才贺少锋姚军锁
邓宗才,贺少锋,姚军锁
(城市与工程安全减灾省部共建教育部重点实验室(北京工业大学),北京 100124)
超高性能混凝土(ultra-high performance concrete, UHPC)是一种新型水泥基复合材料,具有超高强、高抗拉强度、高耐久、高韧性等特点。研究表明[1],提高混凝土强度可以有效减少钢筋用量和截面尺寸,有效降低试件轴压比,进而提高构件的延性和耗能能力。UHPC为结构向轻质高强、高延性方向发展提供了材料支撑,在特殊建筑工程、结构修复及改造等方面应用前景广阔。
国内外对UHPC及其构件性能研究已有长足进展。Voo等[2-3]对预应力UHPC无腹筋工字形梁进行了抗剪试验和理论分析,研究得出提高UHPC中的钢纤维掺量可提高试件抗剪承载力,增大试件剪跨比将降低承载力。陈彬[4]对配置CRB550箍筋的预应力UHPC梁进行了抗剪试验,研究表明掺杂钢纤维可以影响试件的破坏形态,腹筋能明显改善斜裂缝的分布。邓宗才等[5-6]对配置HRB500级箍筋的UHPC梁进行了抗剪试验,结果表明HRB500级箍筋强度能得到充分发挥,混杂纤维和提高配箍率可以提高试件的抗剪承载力。金凌志等[7]研究了高强钢筋UHPC简支梁的受剪性能,研究证实高强钢筋与UHPC协同工作效果良好,在一定剪跨比范围内,适当配置箍筋可以改善试件的受剪延性。此外,一些学者[8-10]对UHPC试件进行了弯曲性能试验研究,结果表明UHPC试件具有良好的弯曲韧性,其开裂应变远高于普通混凝土试件。
赵冠远等[11]对4根剪跨比为8.3的配筋UHPC柱进行了无轴压的低周往复试验,研究表明UHPC柱具有较好的抗震性能;在保证不发生纵筋屈曲及剪切破坏的前提下,可以大幅度减小箍筋的数量及间距。郝文秀等[12]对5个剪跨比为4.3的UHPC空心桥墩进行了低周往复试验和有限元模拟,研究表明UHPC试件具有良好的抗震性能;变形能力和延性随配箍率的增加而改善。鞠彦忠等[13]对18根剪跨比为7.5的普通钢筋UHPC柱进行了低周往复试验,研究表明UHPC柱的延性随轴压比的增大而下降,提高配箍率一定程度上改善了滞回特性。徐慎春[14]进行了12根剪跨比为3.3和5.3的高强纵筋UHPC柱抗震性能试验,试验表明增大轴压比会降低水平承载力和延性,影响试件破坏形态。
然而,以往对UHPC柱抗震性能的研究均为大剪跨比工况,而对剪跨比小于3的UHPC柱破坏规律的研究鲜见报道。为此,本文对5个配筋UHPC柱进行了低周往复试验和理论分析,研究了CFRP布缠绕、配筋强度和剪跨比对UHPC柱抗震性能的影响,为工程设计与应用提供参考。
1 试验概况
1.1 试件材料
1.1.1 UHPC
制备UHPC的原材料有P·Ⅱ52.5R硅酸盐水泥、硅灰、粉煤灰、矿粉、水、石英砂和钢纤维,各组分配比见表1。P·Ⅱ52.5R硅酸盐水泥实测3 d抗折强度7.2 MPa,实测3 d抗压强度34.8 MPa。硅灰的指标:比面积20.2 m2/kg,SiO2含量95 %,烧失量1.3 %,需水量比124 %。粉煤灰为一级粉煤灰,其主要指标:细度(45 μm方孔筛筛余量)6.3 %,需水量比91 %,烧失量1.61 %,含水量1.0 %。矿粉的等级为S95,其主要指标:比表面积418 m2/kg,密度2.88 g/cm3,烧失量0.97 %,7 d活性指数84 %,流动度比99 %。石英砂粒径为10~40目(0.85~2.05 mm)。钢纤维长度为13 mm,直径0.3 mm,长径比43,抗拉强度2 800 MPa。

表1 UHPC材料组成与配合比Tab.1 Composition and mix proportion of UHPC
浇筑试件时预留18个边长150 mm的UHPC立方体试块,与UHPC柱在同条件下养护,试验前测得其立方体抗压强度fcu的平均值为125.6 MPa和劈裂强度ft,s的平均值为19.8 MPa,根据文献[15],取UHPC轴心抗压强度平均值fck=0.88fcu,计算得UHPC的轴心抗压强度平均值为110.53 MPa。预留100 mm×100 mm×300 mm UHPC试块3个,试验前测得弹性模量为56.04 GPa。
1.1.2 碳纤维布
碳纤维增强树脂基(carbon fiber reinforced polymer, CFRP)布为单向编织,编织方向见图1。CFRP布的抗拉强度为3 602 MPa,弹性模量为233 GPa。CFRP布及缠绕效果见图1。

图1 CFRP约束Fig.1 CFRP confinement
1.1.3 钢筋
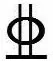
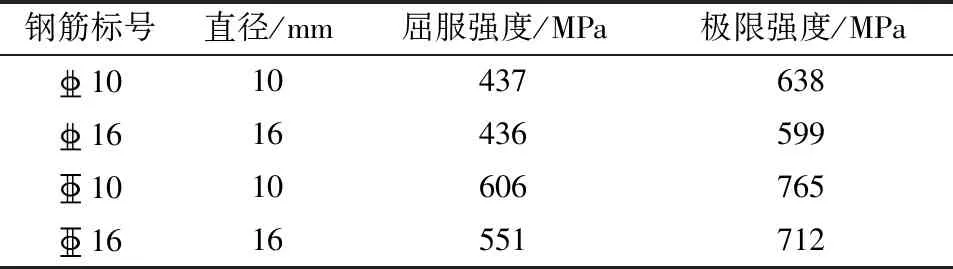
表2 钢筋表Tab.2 Details of reinforcement
1.2 试验设计
试验共设计了5个试件,柱截面尺寸均为250 mm×250 mm,柱高700 mm或1 200 mm,保护层厚度为25 mm。利用UHPC轴心抗压强度,求得试验轴压比为0.2。试验共设置了3种不同约束形式的UHPC柱:LC-2.0为普通钢筋UHPC柱,HC-1.5、HC-2.0和HC-4.0为高强钢筋UHPC柱,为了对比箍筋与CFRP的横向约束效果,设置了一个CFRP布缠绕的普通钢筋UHPC柱LC-2.0F。各试件的参数见表3。
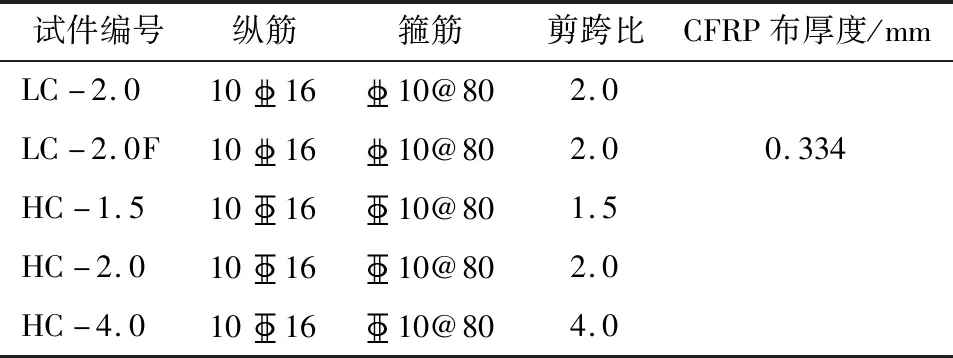
表3 试件参数设置Tab.3 Parameters setting of specimens
试件的详细配筋和尺寸见图2。
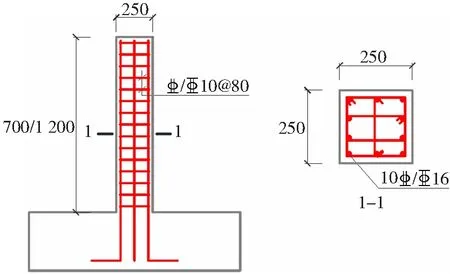
图2 试件详图(mm)Fig.2 Details of specimen (mm)
1.3 加载装置及加载制度
柱顶部施加轴向荷载大小根据轴压比确定,在整个试验过程中保持轴力恒定。根据JGJ 101—96《建筑抗震试验方法规程》,正式加载前先预加载至估算开裂荷载的25 %,检查加载装置是否与试件充分接触、各测量仪器是否正常工作。正式加载时,采用力-位移混合控制的加载方式,试件屈服前采用力控制,依次加载预估屈服荷载的25 %、50 %、75 %、100 %,每级循环一次;试件屈服之后采用位移控制,每级位移为Δy、2Δy、3Δy、4Δy,其中Δy为试件屈服位移,每级循环2次,各级加载后均持荷5 min。当加载承载力下降到最大荷载值的85 %时,试件达到极限荷载,即认为试件丧失承载力,试验结束。加载装置见图3。
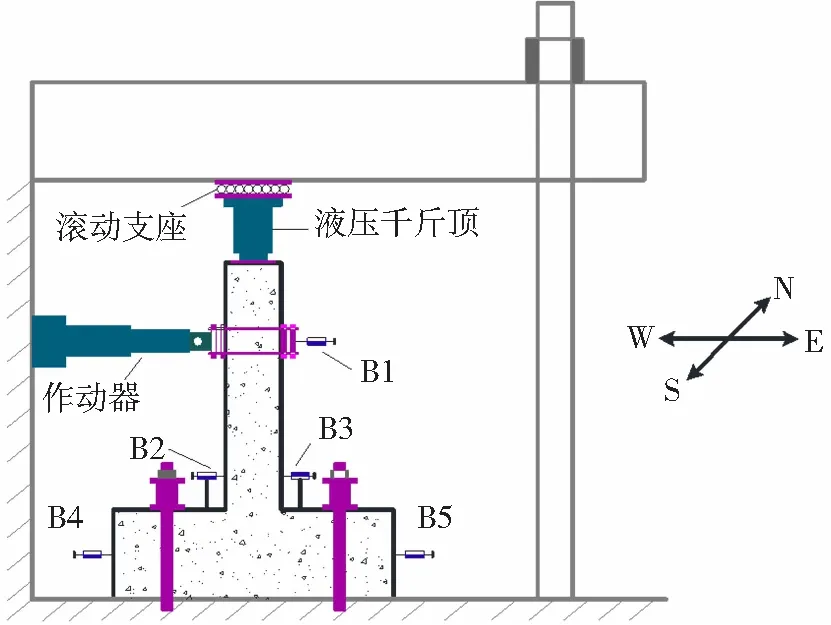
图3 加载装置Fig.3 Diagram of loading equipment
2 破坏形态和破坏过程
5个试件的破坏模式分为两类:剪压破坏和弯剪破坏。当剪跨比较小时,试件发生剪压破坏,如试件LC-2.0、HC-1.5和HC-2.0;当CFRP布缠绕或剪跨比较大时,试件发生弯剪破坏,如试件LC-2.0F和HC-4.0。试件最终破坏形态见图4。

图4 试件最终破坏形态Fig.4 Final failure modes of specimens
2.1 剪压破坏
LC-2.0:当加载至±320 kN时,试件东西两立面出现横向裂缝,最大裂缝长度12 cm;北立面出现斜裂缝,裂缝长度20 cm。当荷载达到±400 kN时,东立面有横向裂缝贯通立面,裂缝呈斜向发展趋势。当加载至±550 kN时,箍筋率先屈服,并有少量纵筋屈服。
HC-1.5:当加载至400 kN时,西立面和北立面分别出现长15 cm和29 cm的斜裂缝。加载至600 kN时,西立面和北立面新增多条斜裂缝,东侧柱底横向裂缝贯通立面,部分箍筋率先屈服。当加载至750 kN时,斜裂缝继续发展,相继有箍筋和纵筋屈服。
HC-2.0:当加载至±200 kN时,出现一条连接东立面和北立面的横向裂缝,裂缝长度10 cm。当加载至400 kN时,西立面出现长7 cm的斜裂缝。当加载至±500 kN时,部分箍筋屈服,卸载时轴力掉载明显。当荷载达到550 kN时,柱底横向裂缝贯通立面,部分纵筋屈服。
2.2 弯剪破坏
LC-2.0F:当加载至400 kN时,西立面出现长6 cm横向裂缝。加载至550 kN时,东西两侧底部的横向裂缝贯通,纵筋受拉屈服,卸载时轴力掉载明显。
HC-4.0:当加载至±200 kN时,东立面和北立面分别出现长14 cm和8 cm的横向裂缝,西立面出现两条通长裂缝和一条长20 cm横向裂缝。当加载至±220 kN时,西立面底部横向裂缝贯通,西侧受拉纵筋屈服。当荷载达到240 kN时,东立面底部横向裂缝贯通,东侧受拉纵筋屈服。加载过程中,裂缝不断扩展,并在位移加载时出现UHPC剥落。
由试件破坏过程看出,对于剪跨比最小的试件HC-1.5,斜裂缝首先出现,并迅速扩展形成临界斜裂缝。而试件LC-2.0和HC-2.0首先在东西立面上出现横向裂缝,接着向其相邻两个立面斜向扩展,最终形成临界斜裂缝,箍筋屈服,横向裂缝贯通试件底部,部分纵筋受拉屈服。对于CFRP布缠绕的试件LC-2.0F,斜裂缝发展受到抑制,箍筋应变增长较慢,在柱底横向裂缝贯通立面后,纵筋先于箍筋受拉屈服,LC-2.0F发生弯剪破坏。剪跨比较大的试件HC-4.0,以横向裂缝发展为主,仅南北立面有少量斜裂缝,且最终未形成临界斜裂缝。
3 试验结果及分析
3.1 钢筋应变
为了说明纵筋、箍筋应力与荷载的关系,部分典型试件的纵筋和箍筋的应力-水平荷载曲线见图5、6。可知,剪切破坏试件(如LC-2.0)的纵筋在位移加载时屈服,而箍筋屈服点与峰值荷载相近。弯剪破坏试件(如LC-2.0F)的箍筋在峰值荷载后屈服,与纵筋屈服时刻相近。剪切破坏和弯剪破坏试件的纵筋和箍筋屈服时,水平荷载均达到或接近峰值荷载,说明配筋UHPC短柱中的钢筋与UHPC变形协调良好,钢筋强度均得到充分发挥。峰值荷载前,LC-2.0和LC-2.0F的塑性变形较小,纵筋和箍筋的应变增长缓慢。峰值荷载后,LC-2.0的纵筋和箍筋应变增幅较大,应变片很快失效,而LC-2.0F在CFRP布约束下,纵筋和箍筋的应变增幅较小,应变片可继续工作。
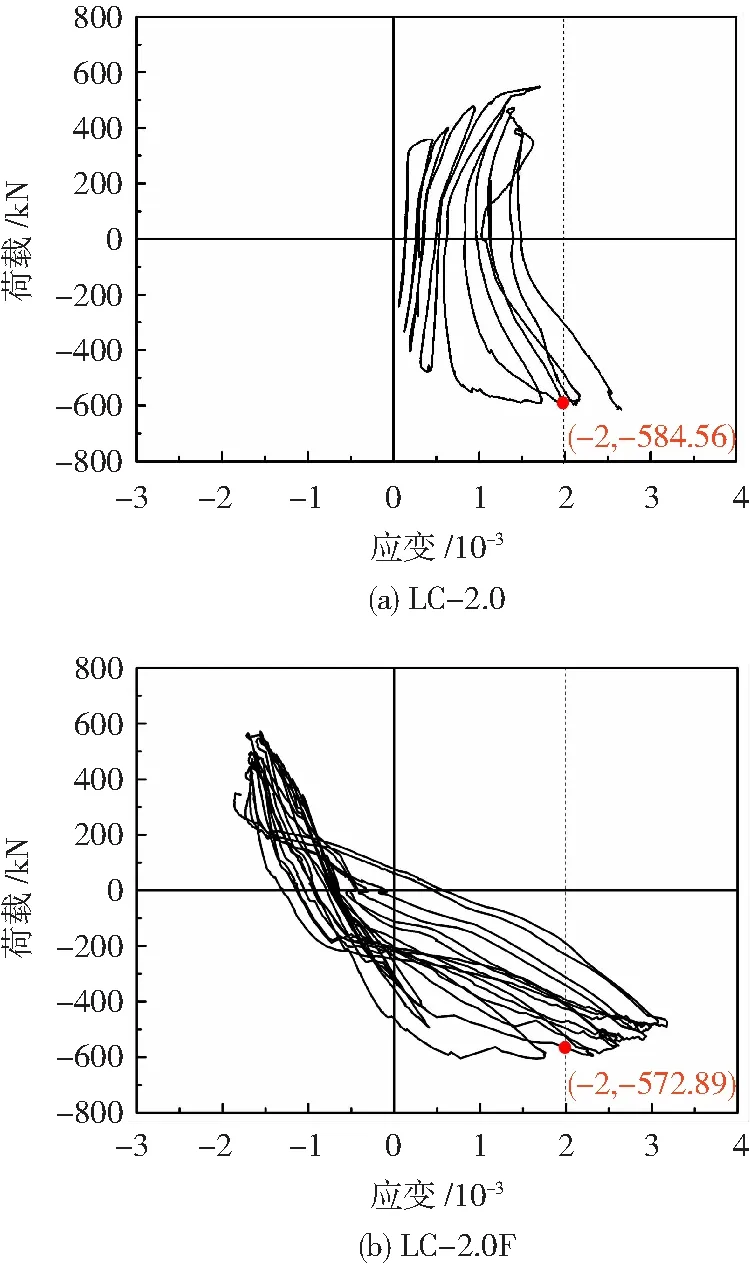
图5 纵筋应力-水平荷载曲线Fig.5 Longitudinal steel stress-horizontal load curves
3.2 水平承截力和延性分析
各试件的特征荷载和特征位移见表4。极限位移取水平荷载下降至峰值荷载的85 %时所对应的水平位移,试件屈服点由通用屈服弯矩法确定。表4中,Fy和Δy表示屈服荷载和屈服位移,Fp和Δp表示峰值荷载和峰值位移,Δu表示极限位移。试件延性系数μ由式(1)确定。文献[16]指出,对于剪跨比小于2的结构构件,用极限位移角θp来评价构件延性更为合适。
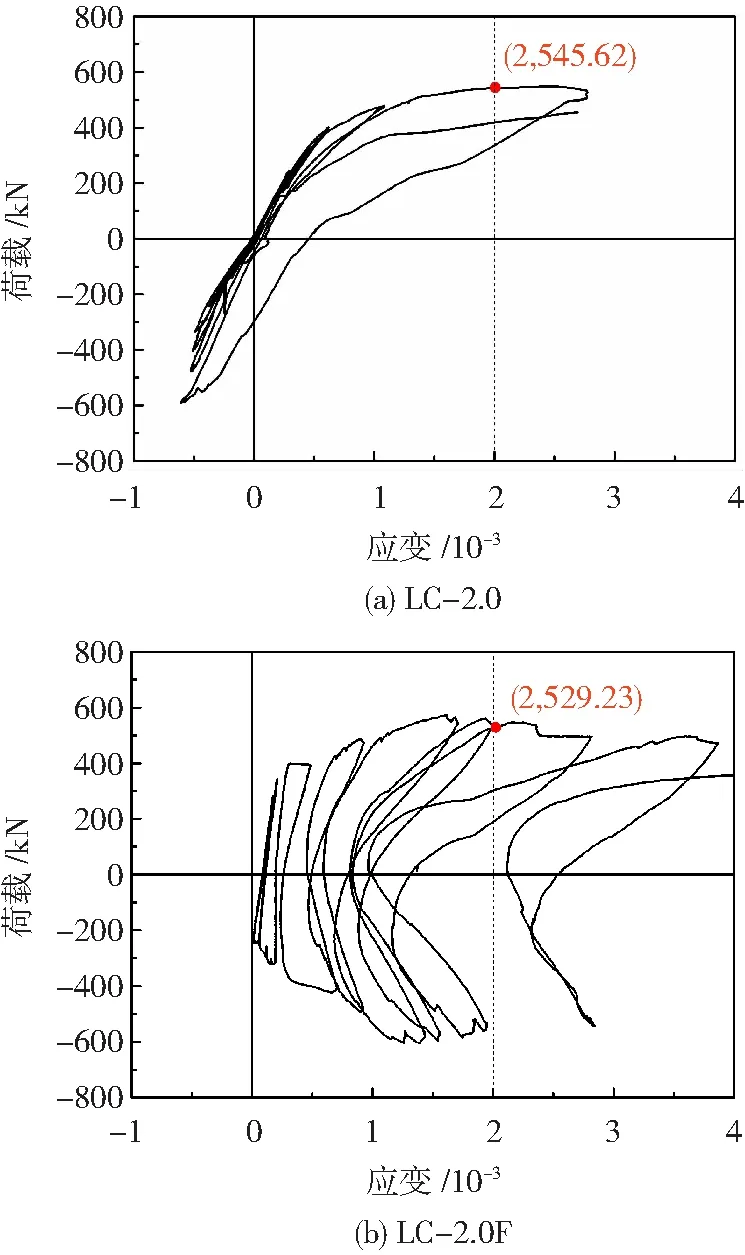
图6 箍筋应力-水平荷载曲线Fig.6 Stirrup stress-horizontal load curves
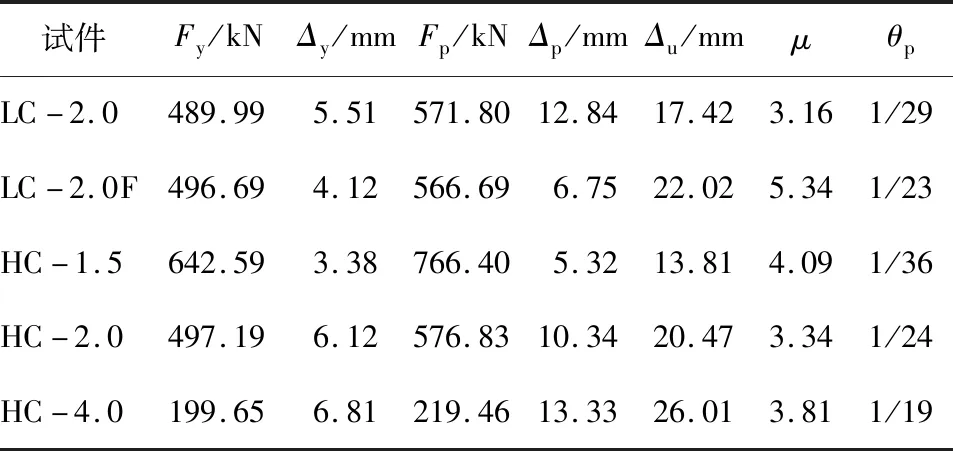
表4 试件的特征荷载和特征位移Tab.4 Characteristic load and displacement of specimens
μ=Δu/Δy
(1)
θp=Δu/H
(2)
式中H为加载点到柱基础顶面的垂直高度。
试件LC-2.0和LC-2.0F相比,LC-2.0F的屈服位移和峰值位移较LC-2.0分别减小了25.2 %和47.4 %,而其水平承载力相近,证明CFRP布可以有效提高UHPC柱刚度,延缓试件裂缝的扩展。试件LC-2.0F的延性系数较LC-2.0提高了71.2 %,说明CFRP布可以显著减缓UHPC柱水平承载力衰减,提高试件延性。
试件LC-2.0和HC-2.0相比,当提高试件纵筋和箍筋的强度后,UHPC柱屈服荷载和峰值荷载有所提高。相较于LC-2.0,HC-2.0的屈服位移有所增加,峰值位移略有降低,极限位移提高显著,延性系数提高了5.7 %。试件进入塑性变形阶段后,高强钢筋可以有效减缓UHPC柱水平承载力衰减,改善试件延性。
试件HC-1.5、HC-2.0和HC-4.0相比,可知试件的水平承载力随着剪跨比的增大而降低,当剪跨比超过一定限值后,UHPC柱发生弯剪破坏。由表4可以看出,无论剪压破坏还是弯剪破坏,UHPC柱均具有良好的延性。
3.3 水平荷载-加载点位移滞回曲线
图7为试件的水平荷载-加载点位移滞回曲线。在加载初期,试件处于弹性工作阶段,滞回环窄小;随着水平荷载的增加,裂缝出现并扩展,曲线由弹性阶段进入弹塑性阶段,箍筋和纵筋逐渐屈服,滞回环趋于饱满,试件耗能增加,滞回曲线无明显捏拢效应,UHPC柱表现出良好的耗能能力。
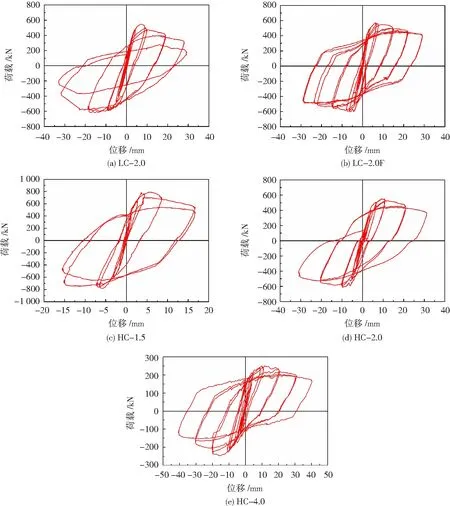
图7 试件加载点位移-水平荷载滞回曲线Fig.7 Displacement-horizontal load hysteresis loops of specimens
不同横向约束方式对比。相较于LC-2.0,CFRP布缠绕试件LC-2.0F的承载力衰减和卸载刚度衰减变缓,滞回环更加饱满。提高钢筋强度后,HC-2.0的承载力衰减较LC-2.0有所缓解,而卸载刚度衰减没有明显改善。
不同剪跨比对比。由试件HC-1.5、HC-2.0和HC-4.0的滞回曲线可知,随着剪跨比的增加,试件的延性和滞回性能显著改善,极限位移提高明显。
3.4 骨架曲线
由于部分试件的剪跨比不同,不能直观地从其骨架曲线比较试件之间性能差异。因此取每个加载循环的最大荷载及其对应的位移作为参考点,将各试件的骨架曲线进行归一化处理,各试件归一化后的骨架曲线见图8。由图8可知,各试件的峰前响应基本一致。而在峰值点后,各试件的延性和刚度退化差异明显。
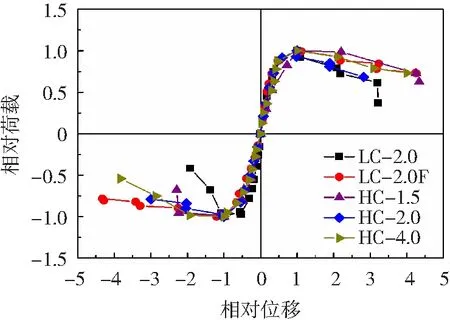
图8 归一化后的骨架曲线Fig.8 Skeleton curves after normalization processing
CFRP布缠绕和箍筋是对UHPC的不同横向约束方式。反向加载时,LC-2.0在水平承载力在峰值点后衰减迅速,脆性特征明显。试件LC-2.0F和HC-2.0的延性分别在CFRP布和高强箍筋的约束下明显改善,刚度退化有效减缓。普通箍筋UHPC短柱的延性相对较差,提高箍筋强度或CFRP缠绕可以改善UHPC受剪构件的延性和刚度退化。
不同剪跨比对比。由HC-1.5、HC-2.0和HC-4.0可知,当剪跨比为1.5时,试件HC-1.5在反向加载时出现明显的荷载突减,脆性特征明显;随着剪跨比的增大,试件的特征位移增大,延性改善。
3.5 耗能能力
用耗能和等效黏滞阻尼系数来表征试件的耗能能力,其计算方法见式(3)、(4)和图9。试件的耗能以滞回环包围的面积来计算,计算耗能值为两次加载循环的耗能平均值。
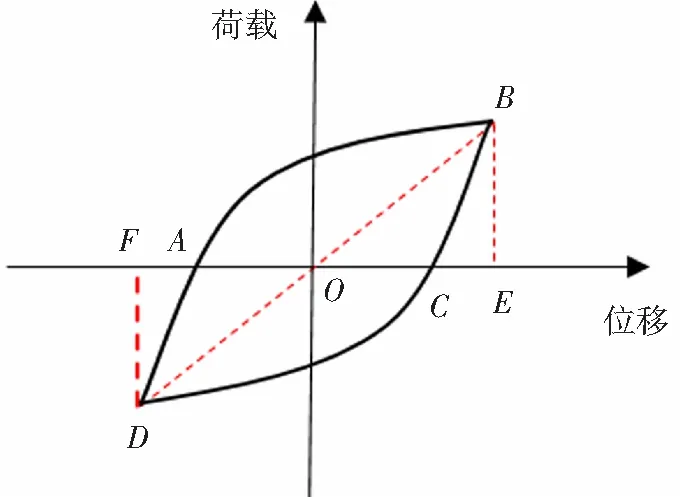
图9 耗能和等效黏滞阻尼系数计算简图Fig.9 Calculation for energy dissipation and equivalent viscous damping coefficient
E=SABC+SACD
(3)
(4)
式中:E表示一个加卸载循环下试件的耗能,ξhyst为等效黏滞阻尼系数,SABC和SACD表示滞回曲线与横坐标轴所围成的面积,SOBE和SODF表示三角形OBE和ODF的面积。
图10为各试件的耗能及等效黏滞阻尼系数与位移之间的关系图。所有试件的等效黏滞阻尼系数均在0.4以上,配筋UHPC柱具有良好的抗震能力。
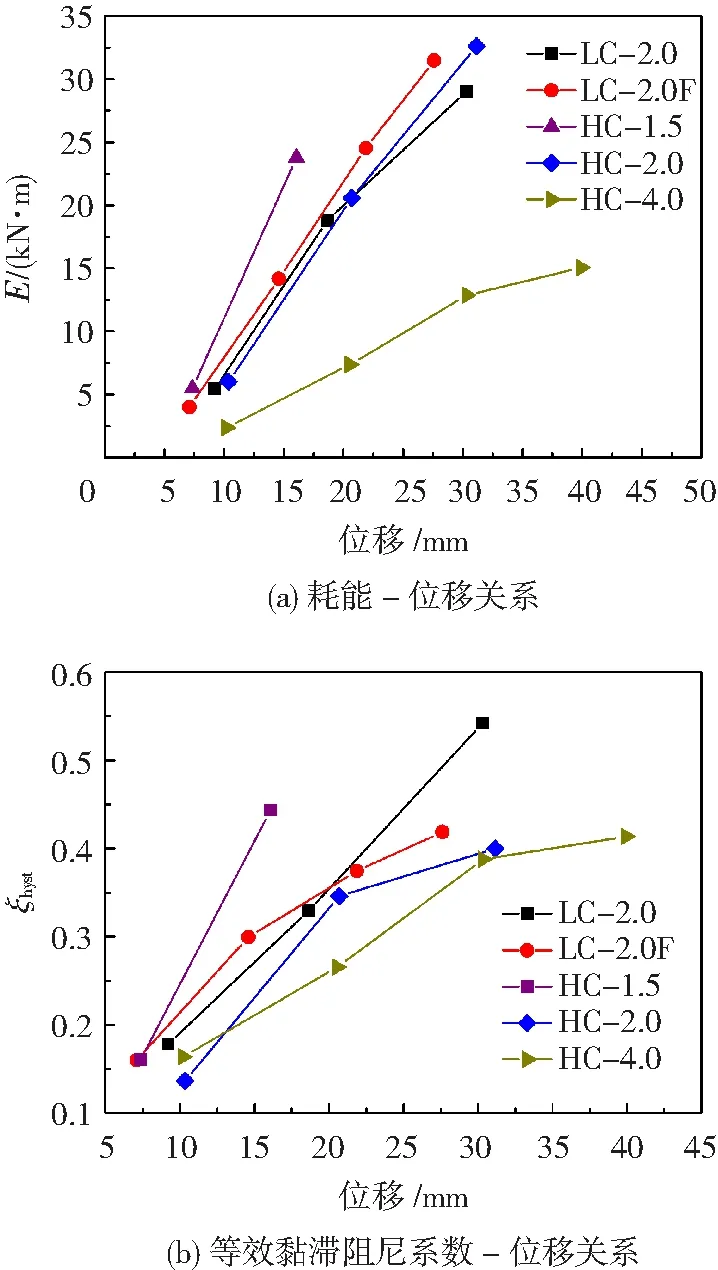
图10 耗能与等效黏滞阻尼系数Fig.10 Energy dissipation and equivalent viscous damping coefficient
不同横向约束方式对比。相较于LC-2.0,试件LC-2.0F和HC-2.0的残余变形较小,等效黏滞阻尼系数有所降低。在加载后期,CFRP布和高强钢筋可有效增强试件的耗能能力。
不同剪跨比对比。由HC-1.5、HC-2.0和HC-4.0可知,随剪跨比的增大,水平荷载减小,试件的耗能也随之降低。在加载后期,随剪跨比的增大,UHPC柱的耗能和等效黏滞阻尼系数衰减加快。
3.6 影响因素分析
3.6.1 钢筋强度
当箍筋屈服强度由437 MPa提高到606 MPa后,HC-2.0的抗剪承载力较LC-2.0提高了1.5 %。UHPC的开裂应力和开裂应变较大,UHPC开裂时,普通箍筋已接近屈服,未能有效抑制裂缝的发展。对于UHPC受剪构件,当箍筋屈服强度小于606 MPa时,箍筋的裂后工作能力较差,脆性特征明显。
3.6.2 CFRP布缠绕
CFRP布的横向约束可以有效抑制斜裂缝的发展,减小试件的变形。CFRP布缠绕试件LC-2.0F的特征位移较LC-2.0下降了25 %~47 %,而特征荷载仅相差1.0 %~1.4 %。由试件的破坏过程可知,LC-2.0F未形成临界斜裂缝,发生弯剪破坏。因此在配筋UHPC受剪构件的设计中,应当考虑CFRP布缠绕对临界斜裂缝倾角和破坏模式的影响。
3.6.3 剪跨比
当剪跨比在1.5~2.0之间时,剪应力和正应力的比值较大,UHPC裂缝以斜裂缝为主,试件发生剪切破坏,且斜裂缝与竖直方向的夹角随着剪跨比的增大而减小;当剪跨比增大至4.0时,剪应力和正应力的比值较小,UHPC裂缝以横向裂缝为主,试件发生弯剪破坏。剪跨比越小,斜裂缝发展越迅速,构件的脆性特征越明显。由试验可知,剪跨比不小于1.5的配筋UHPC柱均具有良好的延性。
4 抗剪承载力计算方法
4.1 UHPC柱抗剪机理分析的桁架-拱模型
利用桁架-拱模型对发生剪切破坏的试件进行承载力分析,见图11。假定箍筋和纵筋只受拉力,考虑混凝土的抗拉贡献,临界斜裂缝形成后,Ⅰ区为零应力区,Ⅱ区为箍筋和UHPC共同作用区域,Ⅲ区UHPC为单向受压的斜压杆。
图11中:V表示试件所受剪力,θ表示UHPC斜压杆与竖直方向的夹角,a为剪力到支座边缘的距离。
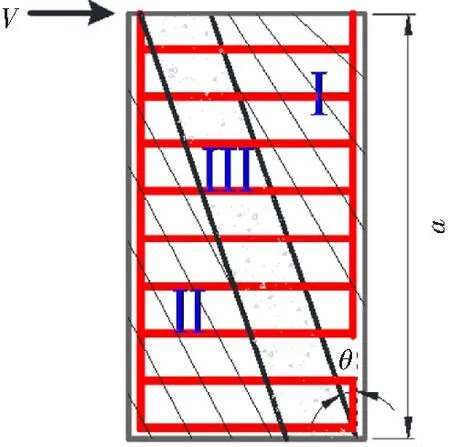
图11 试件的桁架-拱模型Fig.11 Truss-arch model of specimens
试件的抗剪承载力V可以分为由桁架机构提供的抗剪贡献Vt和由拱机构提供的抗剪贡献Va,见图12。图12中:ca为UHPC斜压杆在水平方向的宽度,σa表示试件达到其承载力时,UHPC斜压杆的压应力,α表示临界斜裂缝的倾角,xc表示试件截面的受压区宽度,c为试件的保护层厚度。
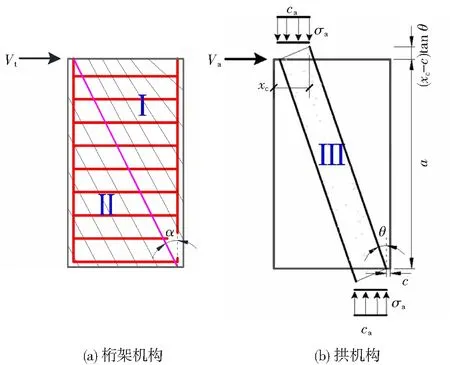
图12 桁架和拱机构示意Fig.12 Diagram of truss and arch mechanisms
4.1.1 桁架机构
分别取桁架机构的Ⅰ区和Ⅱ区为隔离体,见图13。图13中:Vs表示箍筋在水平方向的抗拉合力;Vc表示UHPC在垂直剪切裂缝方向的抗拉合力;σc表示桁架机构中UHPC腹杆的压应力。
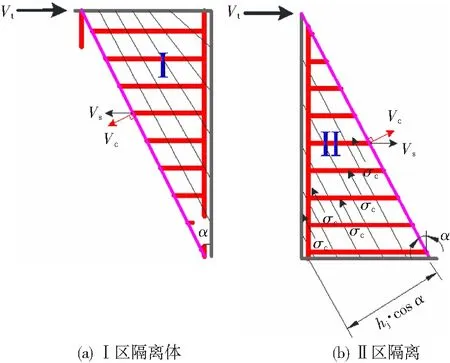
图13 隔离体受力分析Fig.13 Force analysis for free body
考虑UHPC的抗拉作用,剪切裂缝范围内箍筋在水平方向上的抗拉合力Vs和混凝土在垂直于裂缝方向上的抗拉合力Vc分别见式(5)、(6)。
(5)
Vc=ftbhj/cosα
(6)
式中:fyv为箍筋屈服强度,Asv为同一截面内箍筋各肢面积之和,s为箍筋间距,hj为截面两侧纵筋间中心距,ρsv为试件的配箍率,ft为UHPC轴心抗拉强度实测值,b为试件垂直于剪力方向的截面宽度。
由图13(a)可得桁架机构所承担的抗剪承载力见式(7)。
Vt=Vs+Vcsinα=(ρsvfyv+ft)bhjcotα
(7)
根据图13(b)中隔离体的内力平衡,结合式(5)和式(7)可得
Vt=σcbhjcosαsinα
(8)
由1/sin2α=1+cot2α,可得桁架机构中UHPC腹杆的压应力σc为
σc=(ρsvfyv+ft)(1+cot2α)
(9)
文献[17]通过摩尔圆应力分析,给出了考虑轴压影响的矩形箍筋试件临界斜裂缝倾角的计算式:
(10)
式中:kn为轴压比修正系数,取kn=1.8n2-2.25n+1.54;n为试验轴压比;ρsv=Asv/(bs)为配筋率,ρl=As/(bh)为纵筋的毛配筋率,As为纵筋的配筋面积;h为试件平行于剪力方向的截面宽度;ζ1为边界条件系数,根据文献[18],本文取1.57;γE=Es/Ec,为钢筋与混凝土弹性模量比;Av=bhj为试件的有效截面面积,Ag为试件的毛截面面积。由试验可知,当CFRP布横向约束配筋UHPC柱时,临界斜裂缝倾角变大,甚至改变试件破坏模式。
4.1.2 拱机构
1) 拱机构所承担的剪力。拱机构所承担抗剪贡献的计算简图见图12(b)。文献[17]给出了考虑轴力影响的钢筋混凝土柱截面受压区宽度的计算公式:
(11)
式中N为轴力,fc为UHPC圆柱体抗压强度实测值。
文献[19]给出了拱机构中UHPC的强度σa的计算公式:
σa=γcfc-cos(θ-α)σc
(12)
式中γc为UHPC的强度软化系数,取0.7;cos(θ-α)为桁架与拱机构中混凝土斜压杆的倾角差异,取0.9[20]。
将式(9)代入式(12)中,得
(13)
令
(14)
则
σa=(1-η)γcfc
(15)
UHPC斜压杆所承担的抗剪承载力可由式(16)确定。
Va=σab(xc-c)tanθ
(16)
2) 引入剪跨比的影响。剪跨比对抗剪承载力的影响体现在拱机构中斜压杆与竖直方向夹角θ上,由图12(b)的几何关系可得
(17)
把剪跨比λ=a/h和式(11)代入式(17),近似取c/h=0,可得
(18)
4.1.3 钢纤维贡献
研究表明[21-22],UHPC中无序排列的钢纤维可以明显改善混凝土构件的抗剪承载力。文献[23-25]把UHPC的抗拉贡献Vcf视为混凝土基体的抗拉贡献Vc和钢纤维的抗拉贡献Vf之和,钢纤维承担的剪力与钢纤维含量特征值成正比。
Vcf=Vc+Vf
(19)
Vf=k·λfftbhj/cosα
(20)
式中:k为考虑钢纤维形状黏结系数,对剪切平直形钢纤维,取0.45[25];λf为钢纤维含量特征值,取λf=ρflf/df;ρf、lf和df分别为钢纤维的体积掺率、长度和直径。
综上,用式(19)中的Vcf替代式(7)中的Vc,则配筋UHPC柱抗剪承载力公式:
V=Vt+Va=[ρsvfyv+ft(1+kλf)]bhjcotα+
(1-η)γcfcb(xc-c)tanθ
(21)
4.2 抗剪承载力验算
4.2.1 承载力公式对比
运用式(21)及GB 50010—2010《混凝土结构设计规范》中的抗剪承载力公式(22)分别对试验中的试件进行计算,并与试验值作对比,见表5。
(22)
表5中,Vc表示混凝土受压腹杆的抗剪贡献,Vs表示箍筋的抗剪贡献,Va表示拱机构的抗剪贡献,Vcal为承载力计算值,Vcal=Vc+Vs+Va或Vcal=Vc+Vs+0.07N,Vtest表示承载力试验值。VFRP表示CFRP布的抗剪贡献,参考文献[26],由式(23)计算。
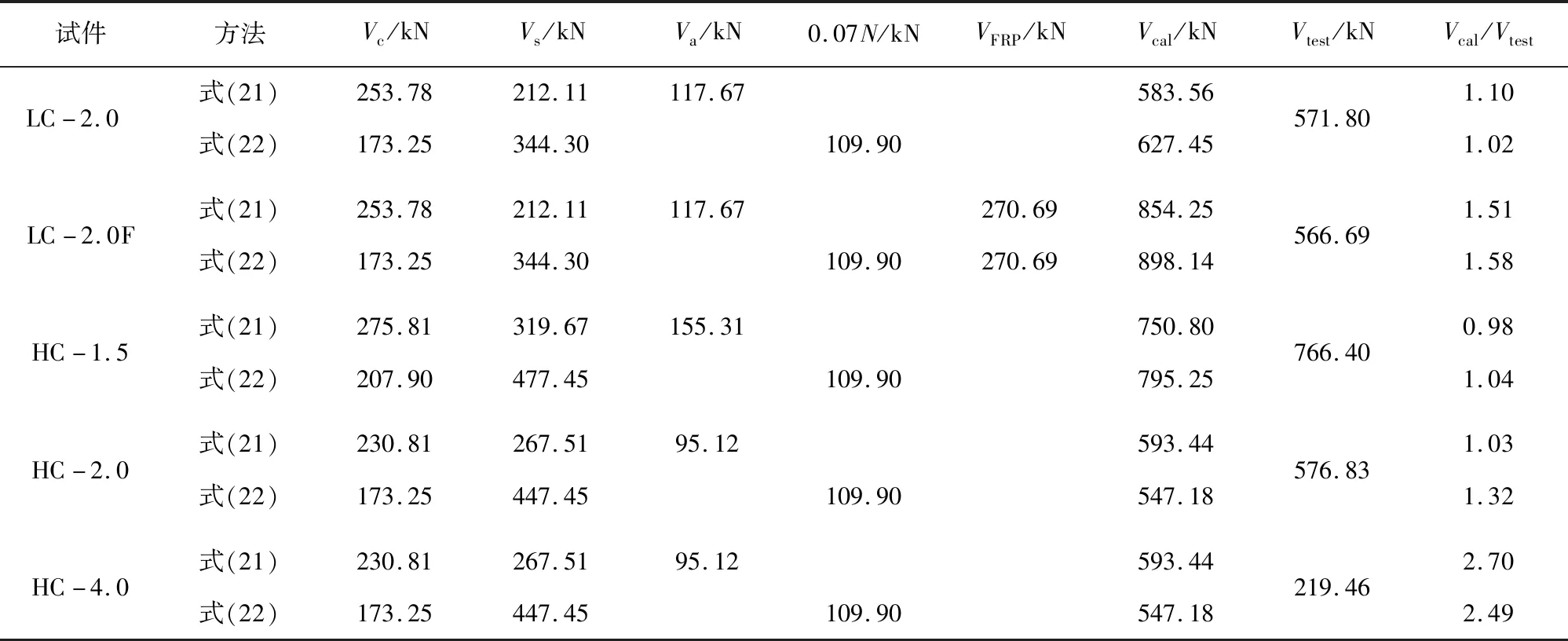
表5 抗剪承载力公式对比Tab.5 Comparison of formulas for shear capacity
VFRP=2fFRP,etFRPhFRP,ecotα
(23)
式中:fFRP,e为CFRP布的有效抗拉强度,取0.5fFRP;fFRP表示CFRP布的受拉强度,tFRP表示CFRP布的厚度;hFRP,e表示试件上粘贴的CFRP布的有效高度,取0.9h;h为试件平行于剪力方向的截面宽度。
由表5可看出,试件LC-2.0F和LC-4.0的抗剪承载力计算值远大于实测水平承载力,进一步说明LC-2.0F和LC-4.0发生弯剪破坏而非剪切破坏。对于其余发生剪切破坏的试件,式(21)、(22)的剪切承载力计算值与试验值之比(Vcal/Vtest)的平均值分别为1.01和1.15,变异系数分别为2.1%和10.5%,说明式(21)对钢纤维UHPC配筋构件的抗剪承载力的预测精度较高。由表5可以看出,式(21)、(22)计算值的主要差异在箍筋的抗剪贡献Vs和UHPC的拉抗贡献Vc上,这是因为式(21)考虑了钢纤维的抗拉贡献、轴压比和配筋对临界斜裂缝的倾角的影响,因此式(21)的计算精度高于式(22)。
4.2.2 适用性验算
为了验证式(21)适用性,从文献[27-29]中选取了15根钢纤维混凝土受剪试件,钢纤维混凝土受压强度为65~134 MPa,钢纤维体积掺率为0.8 %~2.0 %,剪跨比为1.5~2.2。试件的详细参数见表6。
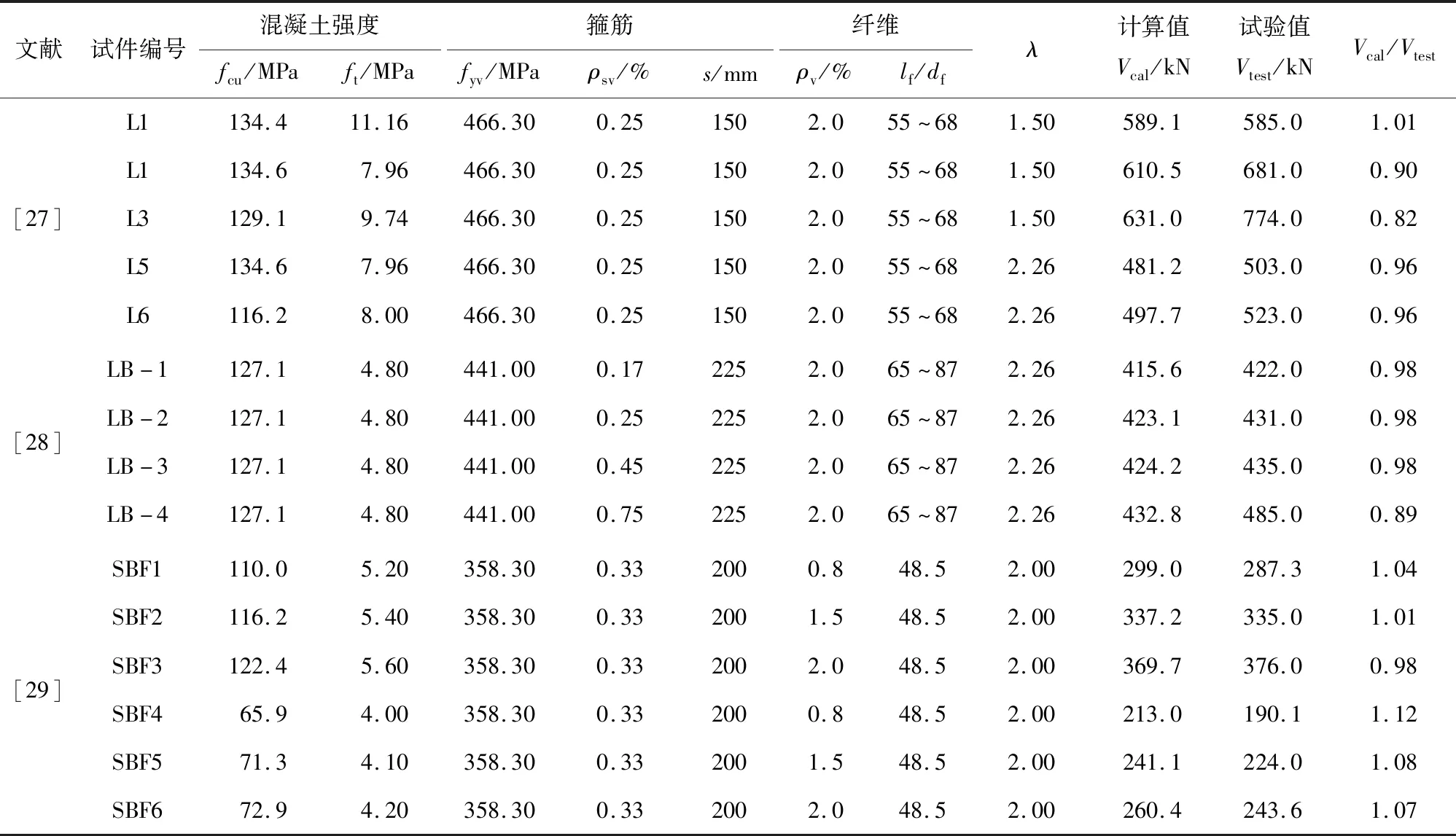
表6 文献[27-29]中受剪试件的承载力计算Tab.6 Calculation of bearing capacity of shear specimens in previous studies[27-29]
利用式(21)对表6中的试件进行验算,计算值与试验值见表6。Vcal/Vtest的平均值为0.99,变异系数为7.6 %,理论计算值与试验值吻合良好。
5 结 论
通过对5个配筋UHPC柱的抗震性能试验和理论分析,得出主要结论:
1) 通过合理配筋,剪跨比在1.5~4.0之间的配筋UHPC柱均具表现出良好的抗震性能。试件的延性系数均在3以上,具有良好的延性。试件的滞回环饱满,无明显捏拢效应,等效黏滞阻尼系数均在0.4以上,具有良好的耗能能力。
2) 剪跨比对UHPC柱的破坏模式影响明显:试件LC-2.0、HC-1.5和HC-2.0等较小剪跨比试件发生剪压破坏,试件以斜裂缝为主,斜裂缝发展较快,脆性相对明显;较大剪跨比试件HC-4.0发生了延性较好的弯剪破坏,试件以横向裂缝为主。
3) 在CFRP约束下,试件LC-2.0F的屈服位移和峰值位移较LC-2.0分别提高了25.2 %和47.4 %,延性系数提高了71.2 %。CFRP布有效约束了斜裂缝的发展,LC-2.0F发生弯剪破坏,延性明显改善。
4) 提高纵筋和箍筋的强度后,试件HC-2.0的承载力和延性系数较LC-2.0有所提高,峰值荷载后水平力的降低速率减缓,抗震性能得到改善。普通箍筋的裂后工作能力较差,UHPC受剪构件的箍筋屈服强度应不小于600 MPa。
5) 基于桁架-拱模型,给出了考虑UHPC抗拉贡献、轴压比和剪跨比影响的抗剪承载力计算公式,计算值与试验值吻合良好。