负荷模型对电力系统失步振荡特性的影响

马伟哲，程维杰，张仕鹏，许琴，✉

（1. 深圳供电局有限公司，深圳518000；2. 中国能源建设集团广东省电力设计研究院有限公司，广州510663）

电力系统由发电机、输电网络和负荷终端等主要元件组成［1］。负荷作为最终消耗有功功率的部分，对系统的稳定起着十分重要的影响［2］。前期的大量研究表明，不同的负荷模型对系统功角稳定、电压稳定、频率稳定均有不同的影响，甚至会产生颠覆性的变化［3-4］。

目前，国内失步解列装置中的失步判别原理主要有3 种：Ucosφ法、相位角法、循序阻抗法［5-8］。三种判据的数学表达式均与站点电压及电压、电流的相位角有关，另外，振荡中心的位置变化也与两侧电压幅值有关。因此，从理论角度分析，负荷模型对系统的失步振荡特性同样也具有重要影响。

为此，本文以某大型电网为研究对象，采用中国电力科学研究院的BPA 程序，开展仿真分析计算。重点从不同负荷模型对振荡中心的位置及失步解列装置的动作情况方面来分析对系统失步振荡特性的影响程度。

1 负荷模型的介绍

负荷模型一般分为静态负荷模型、动态负荷模型及综合负荷模型［9-12］。

1.1 静态负荷模型（ZIP）

静态负荷模型通常采用恒定阻抗、恒定电流和恒定功率的线性组合来表示。某些时候，为了分析负荷的频率特性，在ZIP 模型之中，可以加入一个频率因子。ZIP静态负荷模型如式（1）：

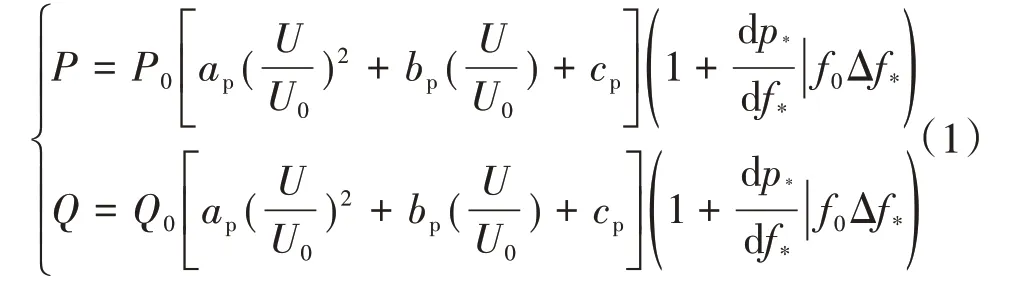
式中：P0为有功功率初始值（MW）；Q0为无功功率初始值（MW）；电压二次项相当于恒定阻抗负荷，电压一次相当于恒定电流负荷（I），电压零次项相当于恒定功率负荷为负荷的频率特性。

1.2 动态负荷模型

动态负荷模型结构由非机理式和机理式两大类。机理式均是以感应电动机模型为基础，有三阶机电暂态模型和一阶机械暂态模型等，其中三阶模型能较好的反映感应电动机动态特性。

1.3 综合负荷模型

采用三阶感应电动机并联负荷静态特性的综合负荷模型结构，是目前最常用的模型。通过设置不同的占比，产生不同的负荷模型。如华东电网采用的60%感应电动机并联40%恒阻抗、南方电网采用的50%感应电动机并联50%恒阻抗等。

2 算例仿真分析

2.1 仿真网络

以某大型电网500 kV 主网架为例，如图1 所示。选取直流1+直流2双极闭锁稳控拒动和XLS站三相故障主保护拒动出线全失2 个故障作为算例，重点研究对断面1 的振荡中心特性及失步解列装置动作情况的影响。其中，直流1+直流2 双极闭锁稳控拒动故障导致大量潮流迂回到交流断面上，引起区域间断面1 失步振荡；XLS 站三相故障主保护拒动出线失压导致断面1 的一个通道断开，引起断面其他通道失步振荡。失步解列装置动作判据采用Ucosφ轨迹法。主要算例采用3 种负荷模型：（1）综合负荷模型：50%Ⅲ型马达+50%恒阻抗模型；（2）静态30%恒阻抗+40%恒电流+30%恒功率模型，简称静态3-4-3ZIP 模型；（3）70%Ⅲ型马达+30%恒阻抗模型。马达参数为：定子电阻Rs0.02，定子电抗Xs0.18，激磁电抗Xm3.5，转子电阻Rr0.02，转子电抗Xr0.12，惯性时间常数Tj2。

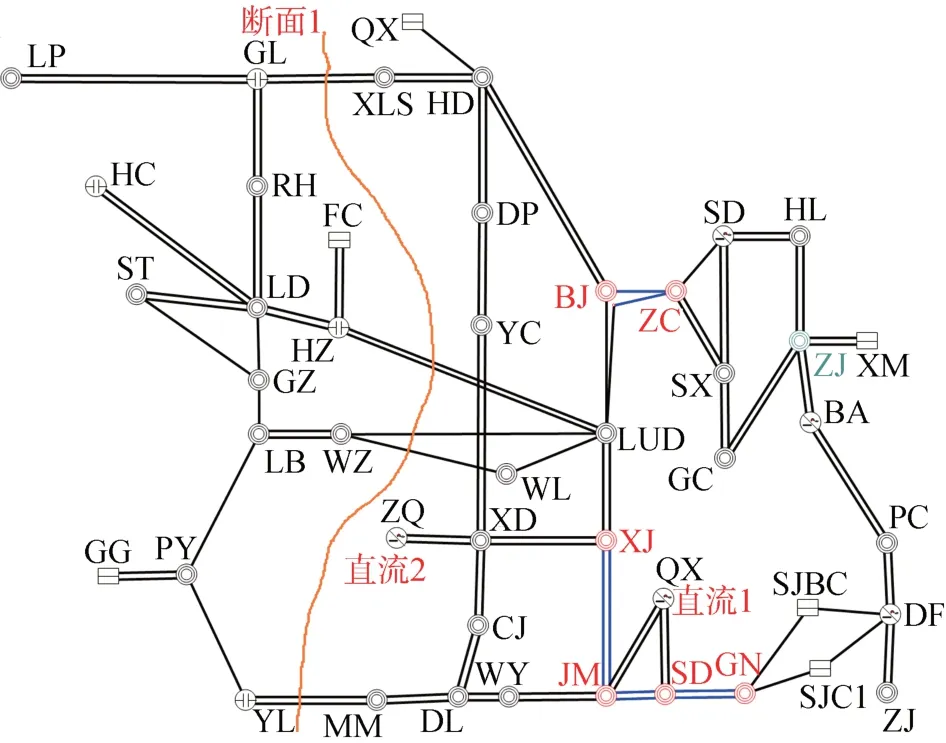
图1 某大型电网500 kV主网架示意图Fig.1 Schematic diagram of the 500 kV main grid frame of a large grid

2.2 对振荡中心的影响

以直流1+直流2 双极闭锁稳控拒动故障为例，经仿真分析，采用不同的负荷模型，振荡中心均位于断面1 附近（GL-XLS 线、LD-HZ 线、HZ-LUD线、LB-WZ 线及YL-MM 线），不同之处是在HZLUD通道上，采用不同的负荷模型振荡中心的位置有所不一样，详见图2。由图2可知，采用ZIP模型时，振荡中心在HZ-LUD 线上；采用50%Ⅲ型马达+50%恒阻抗模型时，振荡中心前2 周期在HZLUD 线后迁移至LD-HZ 线；采用70%Ⅲ型马达+30%恒阻抗模型时，振荡中心主要在HZ-LUD 线上。总之，负荷模型的不同将影响振荡中心的迁移变化。

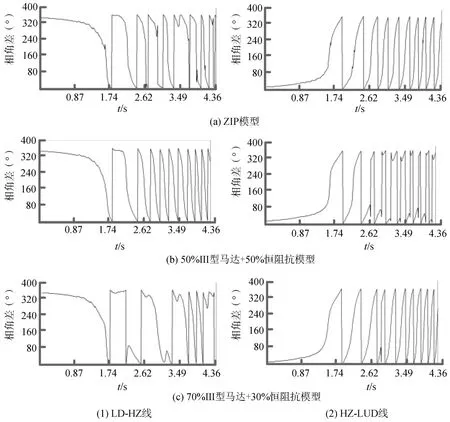
图2 LD-HZ线和HZ-LUD线的两侧相角差曲线Fig.2 Phase difference curve of both sides of the LD-HZ and HZ-LUD lines

其主要原因是由于负荷模型的不同，将导致线路两侧的电压幅值差值不等，从而影响到振荡中心的位置。

2.3 对失步解列装置动作的影响

以直流1+直流2 双极闭锁稳控拒动故障时GLXLS 线XLS 侧、HZ-LUD 线HZ 侧、WZ-LUD 线WZ 侧、YL-MM 线MM 侧Ucosφ曲 线 为 例 进行分析。由图3 可知，采用ZIP 静态负荷模型，线路Ucosφ曲线周期完整性最好，两广断面所有线路均能正确判出并解列断面；但随着感应电动机类型负荷的占比增加，Ucosφ曲线周期完整性变差，甚至会导致失步解列装置能否动作的结论发生颠覆性变化。如WZ-LUD 线WZ 侧Ucosφ曲线，采用ZIP 负荷模型，第二周期幅值范围为［-1，1］，采用70%Ⅲ型马达+30%恒阻抗模型，第二周期Ucosφ幅值范围为［-0.26，0.42］。根据装置的逻辑判别原理，Ucosφ幅值从大于0.3的值穿越到小于-0.3，才算完成一个周期，因此，存在采用70%Ⅲ型马达+30%恒阻抗模型时，周期定值整定为2 时，WZ 侧失步解列装置不能解开WZ-LUD线的情况。

以XLS 站三相故障主保护拒动出线全失时LUD-WZ 线LUD 侧Ucosφ曲线为例进行分析。由图4 可知，采用ZIP 静态负荷模型，线路Ucosφ曲线周期完整性最好，但随着感应电动机类型负荷的占比增加，Ucosφ曲线周期完整性变差。与直流1+直流2双极闭锁稳控拒动故障算例结论一致。

其主要原因是因为故障恢复阶段马达电磁转矩减小，但机械功率依然保持在较高的水平，随着马达逐渐减小，滑差在短时间内逐渐拉大，马达将从系统内吸收大量无功，导致系统电压降低，所以Ucosφ曲线的周期完整性差；而ZIP 负荷吸收的无功功率与电压同方向变化，在故障后的恢复期间会随着系统电压的下降而下降，在一定程度上缓解了系统的无功缺额，有利于电压的恢复，所以Ucosφ的周期完整性较好。

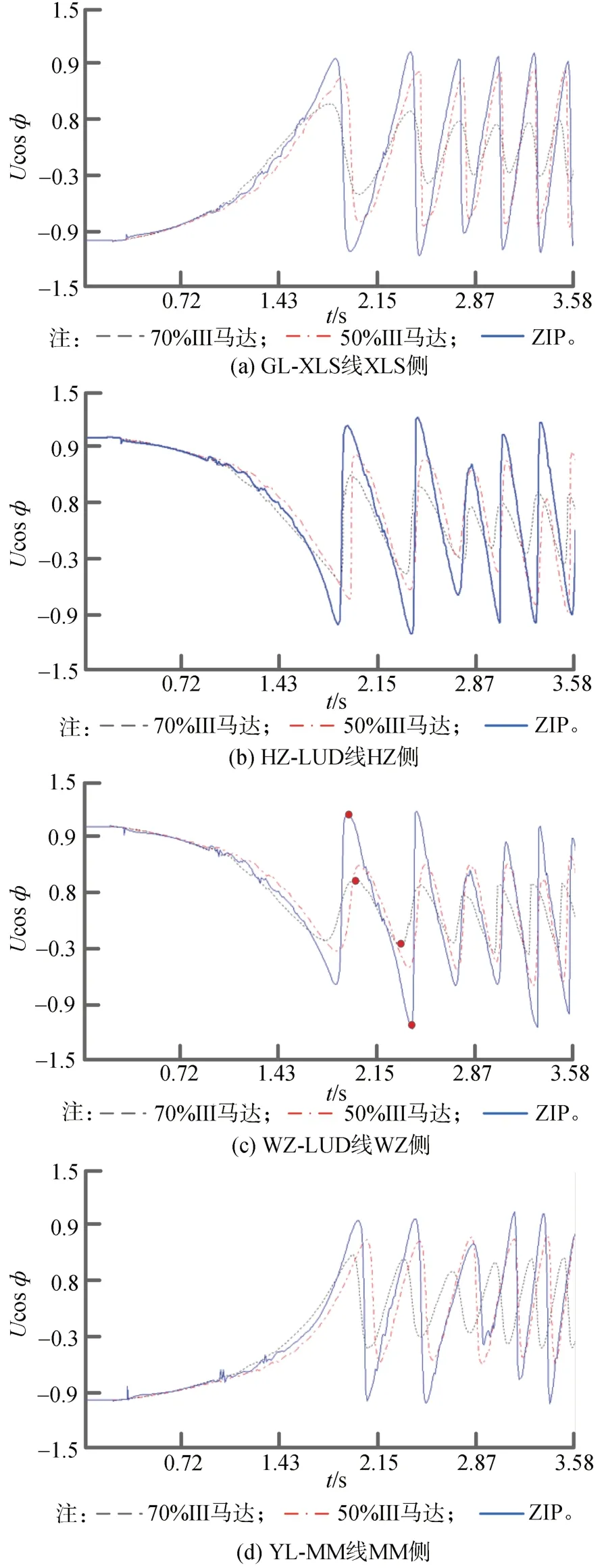
图3 直流1+直流2双极闭锁稳控拒动故障时GL-XLS线XLS侧、HZ-LUD线HZ侧、WZ-LUD线WZ侧、YL-MM线MM侧Ucosφ曲线Fig.3 Ucosφ curve of XLS side of GL-XLS Line，HZ side of HZLUD Line，WZ side of WZ-LUD Line，MM side of YL-MM Line when DC1+DC2 bipolar blocking failure that stability control device refused to move

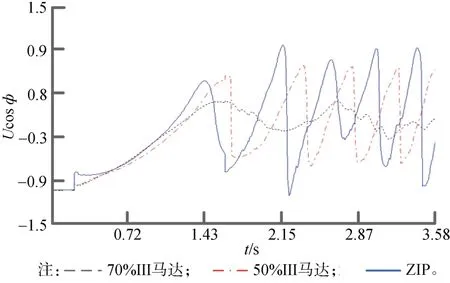
图4 XLS站三相故障主保护拒动出线全失时LUD-WZ线LUD侧Ucosφ曲线Fig.4 Ucosφ curve of LUD side of LUD-WZ Line when XLS station three-phase failur，main protection refusing to operate and failure of all outgoing lines happened

3 结 论

负荷作为电力系统的一个重要组成部分，其模型和参数选择与实际负荷的吻合程度对电力系统相应的失步振荡特性分析结论具有重要影响。

不同模型结构对系统失步振荡特性分析影响很大。以对失步解列装置动作情况的影响为例，采用ZIP 静态负荷模型，线路Ucosφ曲线周期完整性最好；随着感应电动机类型负荷的占比增加，Ucosφ曲线周期完整性变差，甚至会导致失步解列装置能否动作的结论发生颠覆性变化。由仿真结果可知，感应电动机模型所在比重越大，分析结论越偏于保守，甚至有可能是截然相反的。因此，采用最反映实际情况的负荷模型才能有效保证仿真结果的可信度，即不能过于乐观，也不能过于保守。