南极冰盖地表能量平衡的研究进展

杨堤益 丁明虎 邹小伟

研究进展

南极冰盖地表能量平衡的研究进展

杨堤益1,2丁明虎2邹小伟2

(1浙江省海宁市气象局, 浙江 海宁 314400;2中国气象科学研究院青藏高原与极地气象科学研究所, 北京 100081)

南极冰盖地表能量平衡研究, 是耦合冰冻圈、大气圈和水圈过程的基础之一, 对了解冰盖表面物质平衡过程、提升极地天气气候预报水平有着极其重要的意义。随着近年来极地观测水平的提升, 南极冰盖地表能量平衡研究取得了长足的进步, 特别是在辐射参数化和有效热传导系数模拟等方面。但在南极广袤的地域和多样的天气条件下, 已有的研究大都适用于局地环境, 限制了我们的模拟和预测能力。因此, 适用于极地特殊环境的传感器的研发、关键气候区的科学试验的开展和基础的气象站网建设, 能加深我们对冰/雪-气相互作用过程的理解, 进而改进已有的参数化方案, 应用于多圈层模式的耦合。

地表能量平衡 研究进展 南极冰盖

0 引言

地表能量收支指地表向近地表大气或地下空间支出/获取能量的情况, 它主要由地表净短波辐射、净长波辐射、感热通量、潜热通量和地下热通量五部分构成。当它收支达到平衡时, 我们称之为地表能量平衡(Surface Energy Balance): 净短波辐射+净长波辐射+感热通量+潜热通量+土壤热通量=0。

地表能量收支是地球气候系统多圈层相互作用的重要机制之一, 它的各个分量对局地天气和气候的形成有着近乎决定性的作用: 净短波辐射通量作为地表能量的主要输入来源, 补偿因净长波辐射不断释放引起的能量损失, 是地-气相互作用重要的驱动力之一。通过辐射加热/冷却效应, 陆面/水面近表层温度分布会被改变, 呈现出不同的地表感热输送状态; 而热力条件的变化也会使得近地面低层大气饱和水汽压、湿度梯度变化, 产生相变过程从而带走或输入热量, 迫使陆面/水面与大气之间产生不同的潜热交换。此外, 地表下层的温度变化会滞后于地表[1], 不同的温度梯度也会生成指向低温面的热通量, 向地表传输或吸收热量, 调节陆面/水面的能量平衡状态。

南极冰盖总面积约1 400万km2, 平均海拔约为2 350 m, 地形地貌多变。由于特殊的地理位置和水热状况, 它是全球最重要的热汇之一。其表面的冰雪环境能以一些重要的方式改变陆地-大气之间的能量平衡。首先, 南极冰盖的极昼与极夜现象会使得其天气状况具有与中低纬度截然不同的季节变化和日变化。再者, 冰雪的高反照率作为特殊的陆面要素, 改变了表面辐射的收入和支出, 最终可以影响湍流通量和冰雪表层热通量的交换; 此外, 冰雪的存在和强烈的辐射亏损降低了冰盖表面的温度, 与重力作用一起形成了总体指向沿海的压力梯度力(下降风)[2]。作为大尺度极地环流的一部分, 其与南极冰盖地表能量平衡和极向水汽输送的变化有着密切相关, 并把大气圈、冰冻圈和水圈相联系起来[3-4]。

近几十年, 北极海冰快速减少、冰川和冰盖退缩等现象, 引起了世界对“全球变暖”的高度关注。地表能量平衡作为一种有效的研究手段也开始被广泛地应用于冰雪下垫面与大气之间的相互作用中, 特别是南极气候变化的研究[5-7]。基于此, 能量平衡研究的相关国际交流合作纷纷开展, 如国际跨南极科学考察队(http://www2.umaine. edu/itase/index.html), 其目的就是收集整个南极大陆范围的环境参数以评估南极洲在气候变化中的作用。中国南极内陆科考队就曾与澳大利亚南极局合作, 在伊丽莎白公主地建设自动气象站以探究该断面的地表能量平衡分量分布[8-9]; 通过吸纳南极不同气候区站点(South Pole[5]、Neuma­yer[10]等7个站点), 全球地面辐射基线网络(https://bsrn.awi.de)也进一步提高了辐射在南极的系统性监测和研究水平。然而, 在南极恶劣环境的制约下, 虽然有许多或观测、或理论方面的研究发表, 并对南极冰盖地表能量平衡状况进行了计算, 但是大多数的研究对象都位于南极半岛、海岸、近海岸或者海冰区域[6-8], 相比于广袤、地形多样的南极来说, 距离实际需要仍远远不足。所以, 本文拟通过文献调研, 综述南极地表能量平衡的研究方法、研究现状, 并在此基础上总结目前国内外相关领域的发展方向, 对亟待解决的研究重点提出建议。

1 地表能量平衡的研究方法的进展

利用地表能量平衡过程认识气候系统多圈层之间的相互作用, 首先需要可靠的设备对相关物理要素进行准确观测。近年来, 极地的观测技术和冰/雪-气相互作用的模式集成都有了明显的提高, 多种技术方案已经被应用到南极地表能量平衡的研究中。

1.1 观测技术

高水平的观测技术能为我们直接提供高质量的基础数据, 提高研究精度。南极大陆上的气象观测历史已存在一百余年, 而真正系统的气象业务观测则是从1957年国际地球物理年才开始[9]。早期只有很少的有人观测站, 恶劣的气候环境条件也限制了观测传感器的精度。比如Carroll[5]曾在South Pole开展了辐射、冰雪热通量等要素的观测, 并在此基础上对该地区的地表能量平衡进行了初步研究。但由于雪丘和仪器自身结构的影响, 短波观测数据的连续性很差。另外, 低温和强太阳辐射下, 夏季南极内陆的气温测量对辐射引起的热偏差十分敏感, 导致地表能量平衡的计算误差。Genthon等[11]就曾对比了2008年夏季Dome C气象塔和无线探空气温廓线观测资料, 发现即使配置自然通风罩, 气象站气温测量偏差仍能达到1℃以上。

近年来, 随着技术的进步, 特别是电池和通讯技术的进步, 出现了超低温能源方案、铱星数据传输等硬件技术, 极大地提升了极地自动气象观测站的集成水平, 观测数据的准确度和连续性也得到极大提升。可长期自动运行的自动气象观测站逐步得到扩展, 成为了解南极内陆的重要手段, 渐渐填补了一些关键地区的数据空白, 如中国气象科学研究院2011年在伊丽莎白公主地建立的Panda-1(暨Taishan)站, 该站应用了其自主研发的超低温能源系统, 能监测多层风、温、湿、压和辐射变化, 迄今已连续工作近10年[7]。而由于设计目的不同, 不同自动气象站之间存在各自的优势之处。如荷兰乌特勒支大学海洋大气研究所于1997—1998年期间分别在东南极毛德皇后地沿岸、近海下降风区、内陆下降风区建立了具备风、温、湿、压与辐射要素的自动气象站点, Van den Broeke等[10,12-13]以此为基础探究了该区域冰气相互作用在时空上的差异, 并讨论了其机理。而为了研究内陆静稳大气边界层的垂直性质分布和改进总体空气动力学法在极地湍流参数化中的表现, 法国保尔-埃米尔·维克多极地研究所和意大利国家南极研究计划局在Dome C点附近合作建立了Concordia站, 搭建了配置有6层气象要素仪器的45 m气象梯度塔与涡动相关系统来开展相关试验, 并估算了该地区表面动量与感热通量对粗糙度和大气稳定性的影响[14]。据不完全统计, 目前南极地区正在运行的各类自动气象站数目约为110个(图1)。

此外, 无人机、卫星观测技术的发展, 使得获取大范围陆面和底层大气的物理特性成为现实。结合地面气象和冰雪观测, 可以有效将单点扩展到区域研究, 提升模型模拟能力。比如美国的极地轨道环境遥感卫星Terra、Aqua, 其主要用途就是在极轨空间平台上实现对全球大气、海洋、陆地以及太阳辐射的综合观测。而其搭载的中分辨率成像光谱仪(MODIS)则是美国地球观测系统计划中用于观测全球物理过程最为全面的仪器[15]。通过数据匹配, MODIS可以生成积雪和海冰覆盖情况以及气溶胶、云等图像, 被广泛应用于极地和冰冻圈的相关研究中。Scambos等[16]就借助MODIS的后向散射图佐证了东南极中特殊下垫面的存在, 并将其特征纳入了物质平衡模式, 改进了模式的输出表现。Souverijns等[17]利用MODIS的反照率产品观测验证了区域模式模拟的精度。Bozkut等[18]则通过南极半岛异常高温事件前后的两幅MODIS卫星图像直观地说明了强烈的焚风是导致海冰解体的主要原因, 并评估了其对冰冻圈的短期影响。相似的极轨卫星还有欧洲的Envisat、美国NASA的ICE-Sat、我国的风云3号(图2b, c)等, 随着这些遥感手段和衍生产品的发展, 研究大气和海洋/海冰表面状态将更加便捷。

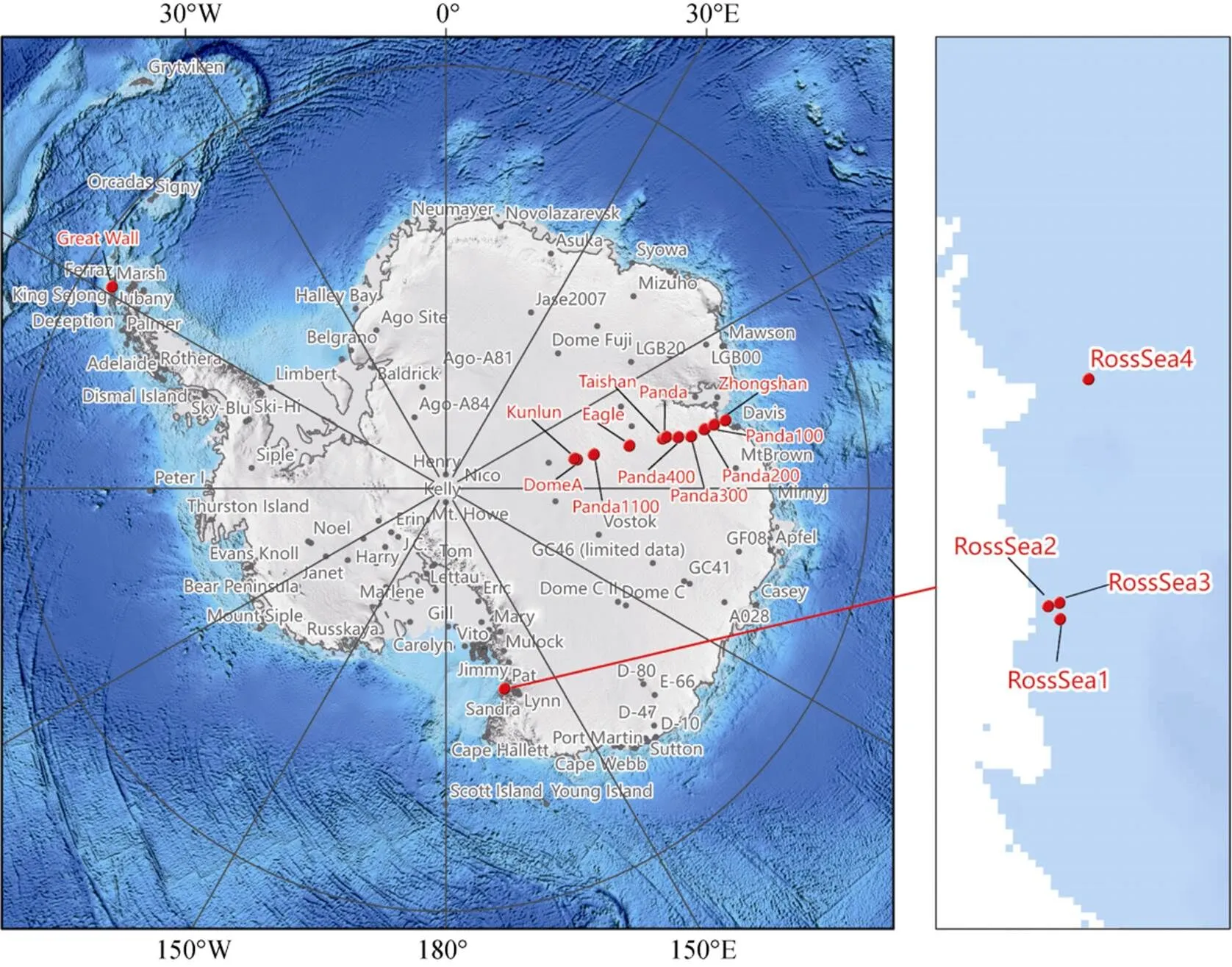
图1 南极自动气象站分布(不完全统计). 红色站点代表中国建设的气象站(包括合作建设站点)

Fig.1. Distribution of automatic weather stations in Antarctica which is incompleted statistics. Red dots represent the stations built by China, including the sites with cooperation

1.2 数值模式

数值模式对天气-气候分析、气候机制发掘和气候预估有着十分关键的作用[19-20]。根据研究区域大小和目标的不同, 模式可以分为单点模式、区域模式和全球模式。单点的天气模式假设水平性质均一, 重点模拟垂直一维方向上能量、物质输送的变化过程, 通常被用于南极代表性区域站点天气气候特征的研究。Bliss等[21]基于单点升华模型对东南极泰勒冰川消融区多点的潜热通量和升华物质损失进行了模拟, 结果证实该模型升华模拟结果与实测消融量有较好的线性相关。并由多点地表能量平衡分布的特征分析指出, 泰勒冰川支流强烈而干燥的下降风是造成该冰川消融带峰值特殊位置的主要原因。而同样是利用单点能量平衡模型, Favier等[22]在阿黛利地蓝冰区结合气象实测和ERA-Interim再分析资料对该地区的地表能量和物质平衡收支变化与气旋入侵内陆的联系作出了讨论。由于忽略了与周围环境的交互效应, 单点模式会存在较强的局地性和自闭型, 但由于简化了计算, 其输出占用的时间和计算资源较小。

在考虑垂直方向能量、物质分布的基础上, 区域天气-气候模式耦合了各个单元之间的能量、物质平流和反馈作用, 能进而描述南极下垫面、能量平衡之间的各种水平差异[20]。此外, 与全球气候模式不同, 区域天气-气候模式格点精度高, 较为全面地涵盖了全球模式中所欠缺的次网格过程, 模式结果往往能准确地反演出南极区域历史冰雪要素的变化, 预估出未来气候的发展。所以区域气候模式渐渐地被广泛应用于两极区域, 去推算海冰、冰盖表面等变化趋势[23-24]。现存南极主要的区域数值模式(表1)大多由中纬度气候模式发展而来。通过评估并改进模式中具体地表能量、云、降水、大气环流或水文过程, 耦合风吹雪、雨雪相态转化等模块, 中纬度气候模式在极区完成改进, 衍生出了一系列不同版本的极区模式。

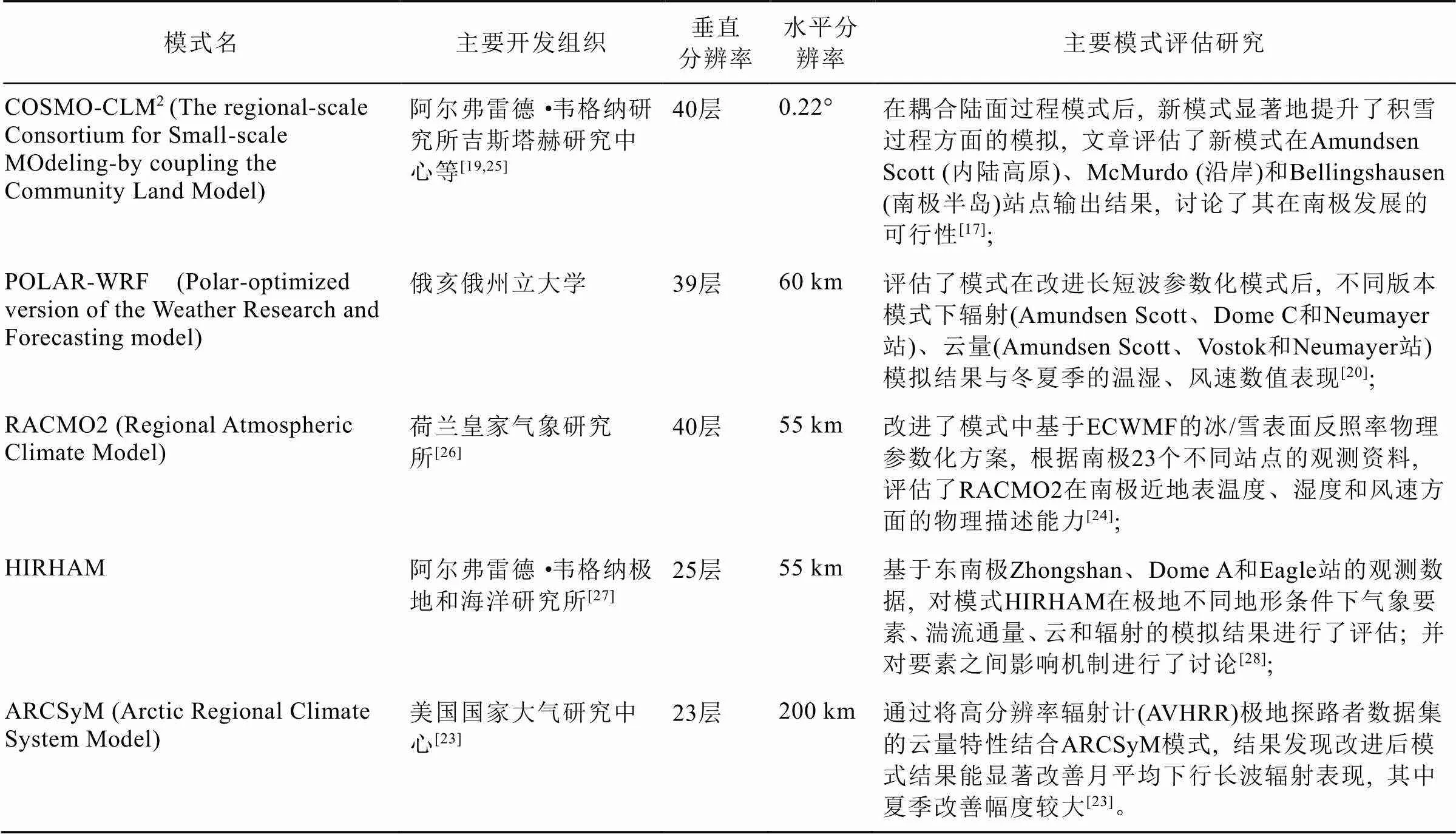
表1 目前南极主要的区域数值模式

全球气候模式覆盖范围广, 能较好地耦合极地环流等大尺度过程与南极之间的联动影响, 也能提供长期的模拟周期, 为研究提供宏观有效的视角去预测未来。Shu等[29]曾对CMIP5中49个模型预测两极海冰的模拟能力进行了评估, 误差分析显示虽然多模式集成海冰厚度模拟结果偏薄, 但对海冰范围的模拟能力较好, 可为良好的地表能量平衡分布式模拟打下基础。Bintanja等[30]通过全球气候模型EC-Earth模拟对比了过去与未来不同情景下南极下降风的强度。结果表明, 全球变暖背景下南极冰盖表面对于大气的冷却作用与其表面下降风强度将明显减弱。这也将导致冰盖表面风吹雪和水汽输送的能力的降低, 造成能量和物质平衡状态的改变。此外, 全球气候模式的缺点也较为明显, 主要表现在时间与计算资源需求较大, 模式空间分辨率通常较低(超过100 km), 使其模型无法充分捕捉典型的南极气候特征, 如下降风和风吹雪现象等[17]。

2 南极地表能量平衡过程研究的主要进展

2.1 短波辐射通量

太阳辐射作为地球系统的主要能量来源, 其传输的物理机制一直是人们研究的重点。随着对其了解的不断深入, 其传输过程被证明往往与日地距离、经纬度、太阳高度角等因子相关。南极冰盖拥有着极高的纬度、相比于中低纬度更低的太阳高度角以及更为干燥洁净的大气和高海拔, 这些导致了其表面特殊的太阳辐射状态[12,31-32]。系统性南极短波辐射的研究开展很早, Yamanouchi[31]就基于POLEX-South计划, 对东南极Mizuho站的附近积雪表面的太阳辐射和反照率进行研究。结果表明, 由于大气气溶胶及水汽含量较低, Mizuho站夏季大气透射比能达到0.75~0.8。Yamanouchi和Shudou[32]同样通过观测分析得到了Syowa站短波辐射分量与云量趋势之间的云辐射强迫关系, 并对其1967—2004年辐射趋势特征进行了细致的分析。另外, 南极冰盖表面下降风区联结着沿海与内陆高原, 沿海大气层顶辐射虽然最高, 但其拥有相比内陆更好的水汽条件, 太阳辐射更多地被吸收在相对较厚的大气中, 形成了沿海向内陆递增的辐射分布。Van den Broeke等[12]曾在毛德皇后地(Dronning Maud Land)的研究中指出, 内陆透射比的增幅可比沿海高25%, 其下降风区站太阳辐射能高至136 W·m–2。而在同样是下降风区但海拔、纬度更高的东南极伊丽莎白公主地泰山站, 杨堤益[33]实测研究发现其相比毛德皇后地具备更高的太阳辐射年均值(156.9 W·m–2)。Dana等[34]对麦克默多干谷11个站点的观测研究则表明, 在周围高地势山脉的阻挡下, 不同地势区域之间的太阳辐射日变化差异能达到两倍, 其区域平均年太阳辐射观测值(84~117 W·m–2)也低于南极冰盖表面其他区域。

反照率对地表能量平衡的影响极大[35]。南极内陆表面反照率很高, 一般在0.8以上, 受极地气旋和东风带波动引起的暴风雪天气影响, 也会有较大的变化[36]。另外, 随着向海岸线靠近, 冰雪反照率在不同的地形地貌上也存在着明显的空间差异[37], Van den Broeke等[12]研究指出云量多且降水事件频繁的沿海地区, 其雪表在夏季吸收的短波辐射量能比内陆地区低65%。但当区域存在焚风效应时, King等[38]指出夏季南极半岛东岸表面反照率会在干热的下沉气流影响下降低(图2a)。其他方面, 下降风的侵蚀和表面强烈的升华作用会使得背风坡区域净积累率显著减小, 而长期作用下会使得雪表颗粒老化变质, 形成类似“釉”一样的表面[39-40], 具有相比沿海或内陆高原冰雪表面更小的反照率和更大的净短波辐射收入[12,16,37]。Jakobs等[35]通过研究沿海Neumayer站24年的表面物质平衡状态, 发现忽略融雪再冻结效应会明显影响雪表反照率, 地表物质损失的速率会被低估2倍以上。现有的冰雪反照率一般基于雪面类型、雪深(冰厚)、雪表面温度等因素计算求得(表2)。Parkinson与Washington[41]较早地提出了根据地表面冰雪存在状态进行分类取值的算法。Roesch[42]和Rinke等[28]则分别通过ECHAM4和HIRHAM中的反照率模型, 提出了单与雪表温度相关的反照率参数化方案。以上方案求算简便, 但在特殊冰/雪面区域存在较大误差。为了进一步提升参数化精度, Briegleb等[43]通过引入光谱波段、雪深、冰厚等因子, 不仅给出了不同冰雪表面状态下的反照率方案, 还考虑到可见光和近红外波段下的反照率结果。该方案在东南极普里兹湾海冰区被Yang等[44]进行了评估和改进, 结果表明当Briegleb方案进一步考虑到天气事件、云量和海冰表面特征时, 反照率结果与实际测值更加吻合。

目前南极太阳辐射观测研究已较为成熟, 且模式结果在多站存在较一致的结果, 但由于极地特殊雪表的存在, 对于模式中反照率模拟的进一步提高需要结合更多冰雪的探测和微物理过程机理。

表2 雪表面反照率参数化方案

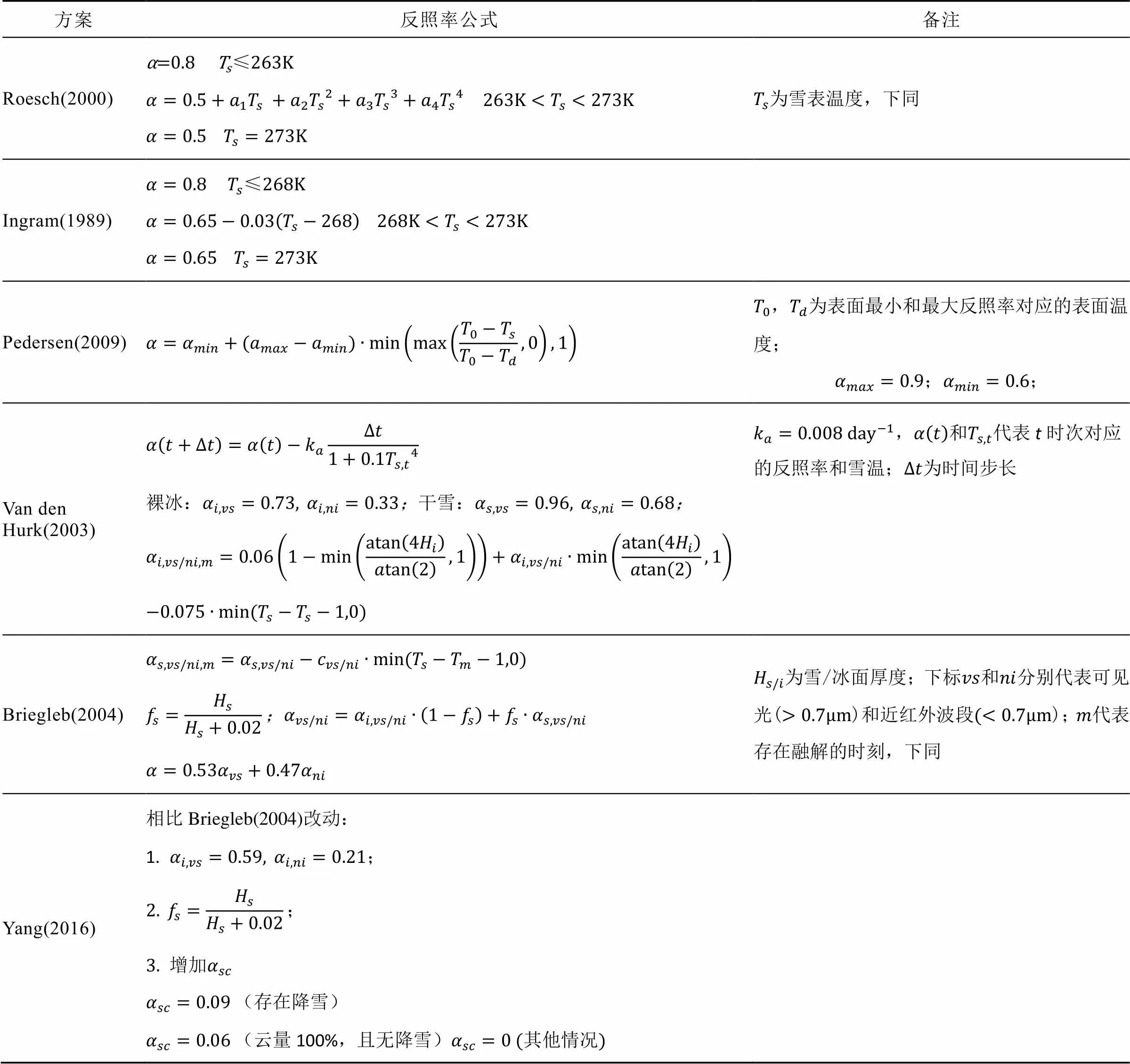
续表2

2.2 长波辐射通量

由于雪表面拥有着接近于1的辐射系数, 所以强烈的辐射放射效应使得雪表不断以长波形式散失热量, 强烈且稳定, 形成了南极内陆大气近表层及其稳定的逆温层[45]。而当冬季极夜期间时, 短波辐射收入缺失, 地面净长波辐射损失使得近地表与大气之间逆温增强, 在重力作用下进一步驱使冷空气下沉, 增强下降风, 间接使得感、潜热通量显著增大以补偿雪表面强烈的辐射能量损失, 但其湍流量级对于地表能量平衡收入的比重仍低至20%以下[7,46], 远小于长波通量水平。

基于斯蒂芬-玻尔兹曼定律, 除了发射率之外, 长波辐射的大小还与放射物体的温度正相关。南极冰盖温度随纬度向内陆递减, 所以会使得冰盖表面存在向内陆减小的地面长波辐射分布(图2b、c), 而且其季节变化也会遵循着地表温度而改变。基于东南极毛德皇后地断面4个不同海拔高度和地形的自动气象站(AWSs), Van den Broeke等[12]对该断面的净长波辐射的时空特征进行了分析, 研究显示内陆站点净长波辐射存在相较于断面其他站点更大的季节变化, 这源于冬季强逆温效应与夏季强辐射加热的剧烈反差。其研究还指出, 由于下降风区对地表持续的感热通量输入, 抬升了地表温度和地面长波辐射, 会使得该下降风区冬季相比内陆和沿海拥有更大的长波辐射损失。此外, 当存在强烈的热量和水汽输送时, 下降风区地表的长波辐射将大大升高[7]。冬春季节也是海洋性气团入侵内陆的多发时期[47], Ding等[7]研究指出一次暖湿气团入侵可使得长波辐射分量各增长60 W·m–2以上, 改变长波辐射平衡状态。Vignon等[48]也证明强烈的气团入侵造成了Dome C站反射长波辐射和地表温度的短时异常上升。

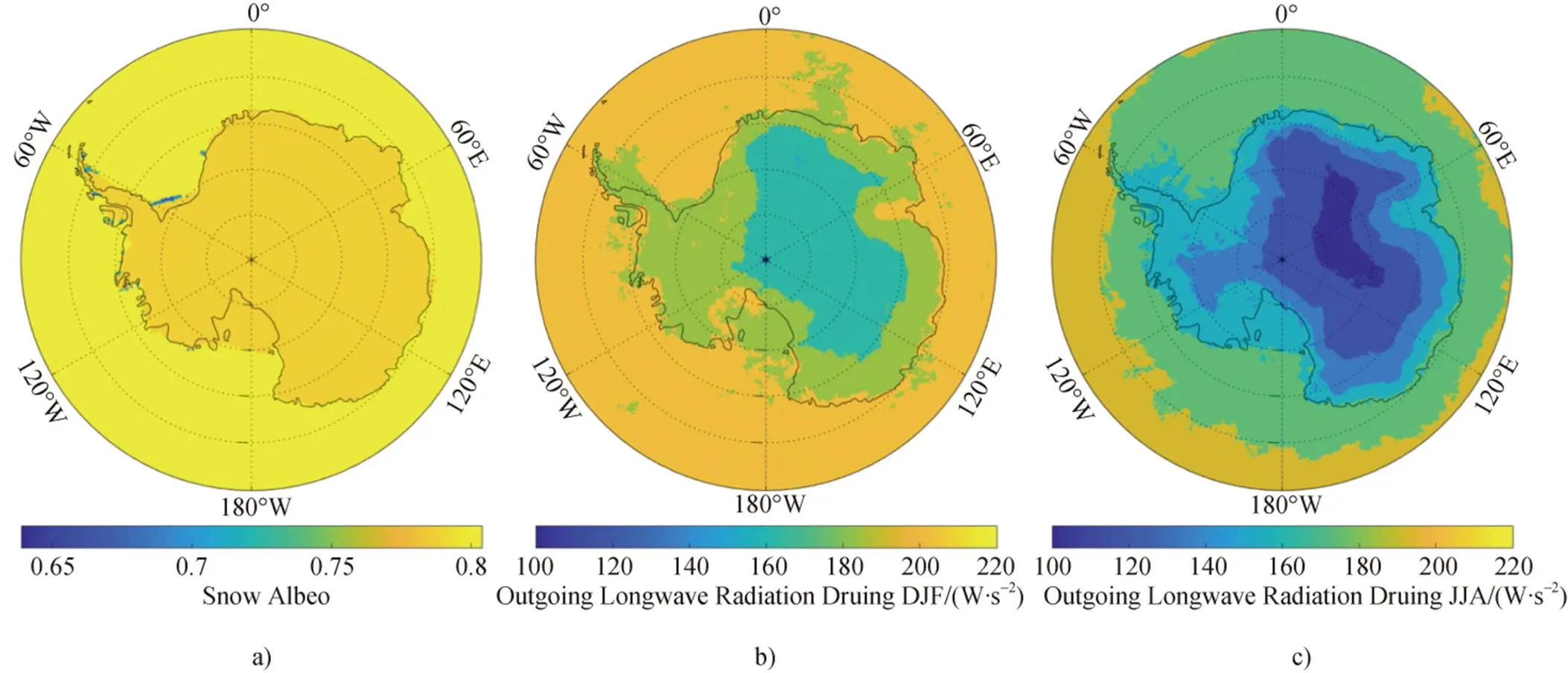
图2 a)2019年12月至2020年2月ERA5雪表平均反照率; b)2019年12月至2020年2月 FY-3D极轨卫星平均地面长波辐射产品(http://data.nsmc.org.cn/portalsite/default.aspx)分布图; c) 2019年6月至8月FY-3D极轨卫星地面长波辐射产品分布图

Fig.2. a) The average snow surface albedo distribution of ERA5 reanalysis datasets from December, 2019 to February, 2020; b) The average outgoing longwave radiation distribution of FY-3D Polar-orbiting Satellites from December, 2019 to February, 2020; c) The average outgoing longwave radiation distribution of FY-3D Polar-orbiting Satellites from June to August, 2019.

参数化方面, 长波辐射参数化的核心在于其辐射系数的模拟。而辐射系数无法直接测量得到, 它会受大气中水汽、温室气体(CO2和CH4等)、气溶胶和云的特性等因子影响。但是除了常规的气象要素之外, 其他因子的测量在南极并不普及, 所以在向下长波辐射研究中, 国内外学者通常使用基于水汽压与气温的参数化方案[49-51]。Ohmura[52]在研究中指出晴空条件下地表得到的向下长波辐射有89%的辐射通量来自于地表以上1 000 m的范围。所以向下长波辐射的参数化中, 天空温度一般使用地面实测气温代替(表3), 并结合地面水汽压间接进行整层大气的长波辐射的参数化。但也有研究[36]指出, 当考虑到受太阳辐射影响所造成的气温波动时, 选用大气逆温层顶部的日最大气温代替地面气温计算将更加稳定。

当云对长波辐射的作用不可忽略时, 云量、云的液态水路径等因子对向下长波辐射也有较大影响[53]。冰/雪面上应用较广的计算方案是Konzelmann等[54]在1994年发展的方法, 该方法下辐射系数为基于云量指数的一元多项式函数。经过与南极下降风区实测资料对比发现, 其结果平均偏差在6%以内, 均方根误差只有15%左右[33]。陈百炼[8]在Konzelmann方案的基础上, 考虑温室气体对向下长波辐射的贡献, 对南极Dome A地区的长波辐射也提出了修正性参数化方案, 进一步提升了该地区的长波辐射参数化精度。除了传统的云量和气温, Ding等[49]考虑到海拔变化对于辐射系数的影响, 应用Liston和Elder[55]方案对Panda-N站长波辐射进行了参数化。该方案考虑因素较为全面, 但适用海拔存在一定限制。此外, Zhou等[53]基于表面温度、云量、云的液态/固态水路径等多个因子建立了全天空下向下长波的参数化机制, 并在高纬多个站点得到了较好的验证结果[56]。但总体来说, 云微物理深层次机理的欠缺对于地表净长波辐射仍存在较大的限制, 依旧是目前限制极地长波辐射发展的核心问题。

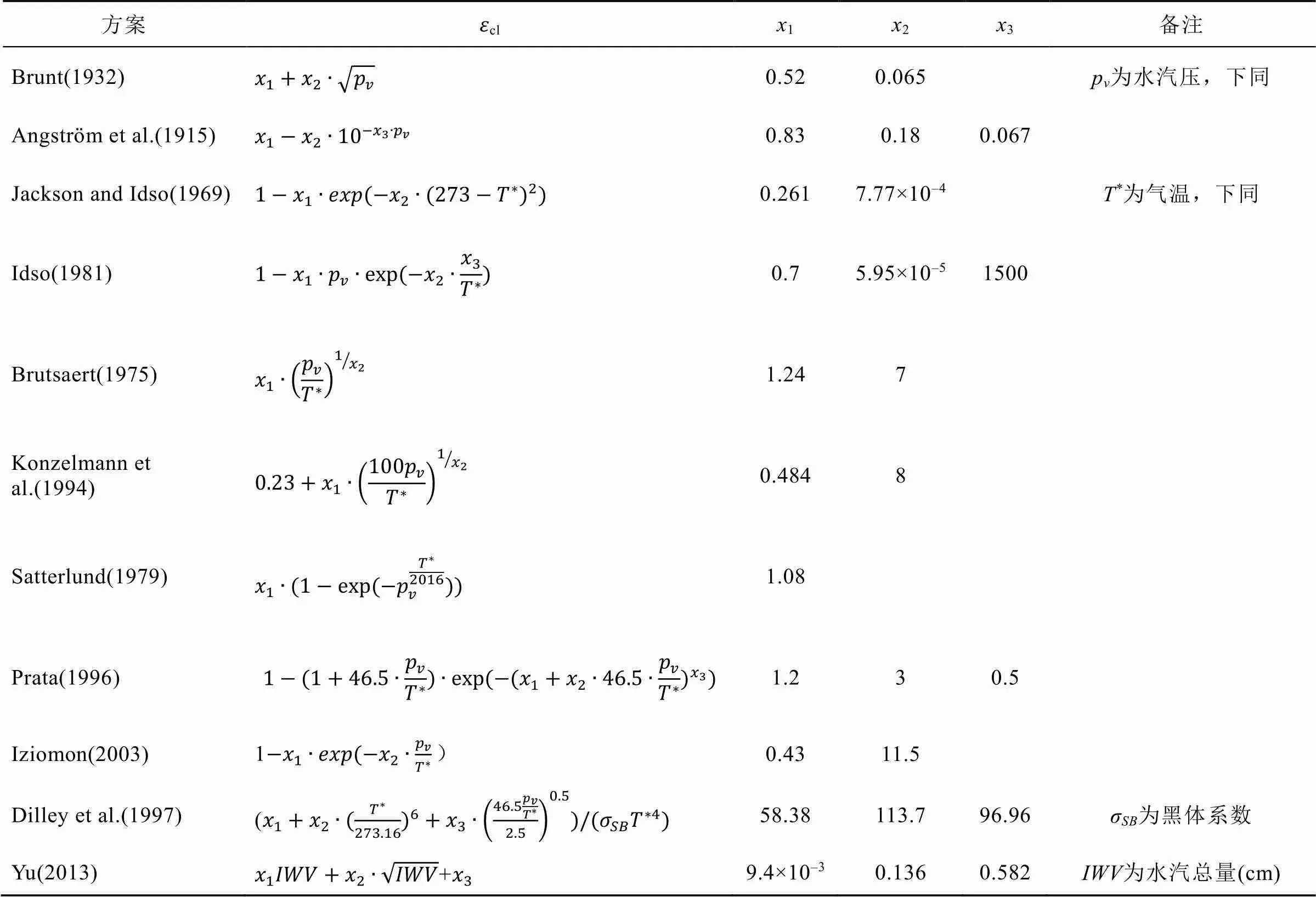
表3 晴空条件下辐射系数参数化方案(改自Gubler等[57])

ε为晴空下辐射系数,为系数

2.3 南极湍流通量研究

湍流通量中感热与潜热分别表示地表与大气之间非相变和相变的热量输送, 它们的传输可以看成地-气水热性质不均一的结果。由于冬季南极雪表强烈的热散失, 湍流热量交换在南极是一项十分重要的能量收入项。而测量湍流通量精度最好的仪器——涡动相关观测系统在极地条件下适用性差, 运行时效短。所以南极湍流研究多基于参数化开展, 但发展至今, 一直是极地冰气相互作用的重点和难点。早期研究中, 南极的湍流通量是通过计算辐射通量的残差项来确定的[5], 这种方式求算简便, 但感热与潜热没有被单独地分离进行研究, 无法区分表面热交换以及相变过程。

随着梯度通量法被用于冰雪地表能量平衡研究[58]以及MO(Monin-Obukhov)相似定理的发展, 冰/雪-气表面湍流通量的计算方式不断地被得到改进。基于MO相似理论的总体空气动力学法是目前极地应用最为广泛的方法, 其假设冰雪表面的水汽始终处于饱和状态, 这样处理的优点在于使得表面的湿度求算简便, 对输入气象数据的精度要求也低。目前为止, 该方法中湍流系数的参数化已存在着多种相似函数(表4), 受其函数普适性的影响, 粗糙度和大气稳定度相似函数的模拟结果在不同边界层条件下会有不同的偏差。当大气弱稳定或存在弱对流时, 相似函数的修正量甚至能达到30%[13], 所以相似函数的选择对于最终湍流计算十分关键。

相似函数表示大气近表层中温度、湿度和水平风速廓线的变化关系, 是表征大气边界层稳定性参量(实际高度/MO长度)的一种固定函数形式。根据南极不同的气候区条件, King和Ander­son[59]、Lettau[60]、Grachev等[61]都各自根据观测建立了函数方案。但这些研究初始条件大都为近中性大气层结, 需要迭代运算进行模拟, 直到MO长度收敛。这类方法虽然结果精度较高, 但是往往会占用较大的运算资源。所以一般在大型气候或天气模式中, 大气边界层稳定性的表征因子由理查逊数Rib代替[62]。而随着相似函数方案不断推陈出新, 其在南极不同区域的表现也在不断被得到评估讨论[9,14,33,63]。Andreas[63]基于稳定大气下, 对冰雪面上6种函数方案进行了评测分析, 结果表明Holtslag(详见Andreas[63])方案结果随着稳定性参量趋近于无穷, 更加符合湍流成为层流的数理规律, 比较适合冰雪环境下大气稳定分层的情形。陈百炼[8]在东南极Dome A展开的模拟研究中指出, Beljaars和Holtslag[64]方案在稳定大气条件下能显著降低对湍流发展的低估, 总体表现较好。而通过与东南极中山站附近的实测涡动结果对比, 马永峰[9]指出Louis方案在不同大气条件下总体具有最佳的误差表现; 相似地, 在泰山站附近下降风区的涡动数据基础下, 杨堤益[33]对8种稳定与4种不稳定大气条件下的相似函数进行了验证, 分别得出了对应条件下Beljaars与Lettau方案最优的结论。

表4 不同稳定层结大气下相似函数参数化方案

Table 4. Parameterizations of similarity function under stable/unstable atmosphere conditions

粗糙度是表征陆面过程的基本参数, 是由相似理论外推出相应特征要素与地表值相等的高度[65],与下垫面类型有着十分紧密的关联, 目前冰雪表面动量粗糙度的计算方法一般是利用两层风速关系计算求得。但在其随时间变化研究上, Van As等[66]认为低温能很大程度上减缓雪晶转变, 进而阻碍雪表粗糙元随时间的变化。基于该观点, Van As等根据实测数据假设雪表粗糙度为常值(z0=2×10–5m), 并对Kohnen站展开了地表能量平衡的夏季研究。Van den Broeke等[13]也曾基于涡动数据分别得到了近中性大气条件下毛德皇后地内陆下降风区和内陆高原站的粗糙度(1.6×10–4m和2.1×10–5m), 并成功用于感热的计算。上述假设条件下, 湍流计算简便, 但是在极地的高风速环境下, 雪表表面形态被塑造各异, 雪表粗糙度变化与分布复杂[37]。忽略了粗糙度随密度、雪龄等性质的变化, 会存在一定理论缺陷。Inoue[67]和马永锋[9]研究指出风吹雪过程以及风向的变化会使冰雪表面雪丘方向再分布, 当雪丘与风向存在夹角时, 雪表面对空气的拖曳作用会变大, 最终增大雪表动量粗糙度的量级, 其时间变化是不可忽略的。而基于粗糙度变化的重要性, Van den Broeke等[10]随后在Neumayer站使用10 m与2 m风速计算了粗糙度的时间变化; 非吹雪条件下时, 沿用了Kongig-Langlo的典型值(z0=1×10–3.5m)对沿岸的地表能量平衡、融解和升华机制进行了研究。而空间分布研究方面, 马永锋[9]基于Dome A、LGB69和中山站站点的数据计算结果分析认为, 沿岸和内陆高原的动量粗糙度一般以强下降风区值最大。而热量和水汽粗糙度方面, Andreas[68]在1987年基于温湿廓线数据得出了冰雪面上热量/水汽与动力粗糙度比随雷诺数对数变化的规律, 被得到了广泛的应用[7,13,66]。但由于缺乏验证数据, 其水汽粗糙度在低温下的误差表现尚无定论, 仍需要更多的观测数据去验证评估[14,63]。

在重力和气压梯度力的共同作用下, 南极冰盖表面坡度较大的海岸及其与内陆的过渡带易发生强下降风。在下降风区持续强而稳定的地面逆温、高风速等因素联合作用下, 该区域大气通常是强稳定而干燥的; 同时, 当大尺度压力梯度力较弱时, 冬季沿岸冰架与海冰上堆积的冷空气对下降风具有缓冲作用[69], 所以下降风区雪表面总体拥有着相比沿海站更高的感热和更低的潜热[12-13](图3)。马永锋[9]在CHINARE断面各站点夏半年的研究中指出, 感、潜热通量分别拥有着从沿岸向内陆增大和减小的特征。Thiery等[70]与Van den Broeke等[13]在东南极毛德皇后地断面上的站点研究结果也验证了该特征。而当下降风风力超过一定阈值时, 不仅能增大湍流交换, 甚至能产生风吹雪现象影响地表粗糙度的变化[16]。此外, Bintanja[71]夏季在瑞典Svea站附近观测发现南极蓝冰区和相邻雪表面拥有不同的感热通量传输方向, 其分析认为蓝冰区对太阳辐射吸收增强的响应是造成该差异的主要原因。King等[72]对具有相似纬度的沿海冰架Halley站、内陆高原Dome C站湍流通量日变化进行了分析对比, 结果认为两站存在不同日变化的主要原因在于潜热通量在两站地表能量平衡中的不同贡献。同时也有研究表明, 不仅仅是下垫面, 天气系统也会影响表面的湍流特征。比如: Ding等[7]通过下降风区泰山站的冬季湍流通量结果与东南极大气环流形式、水汽通量输送状态进行了结合分析, 结果认为海洋暖湿气团入侵能造成内陆表面湍流通量的短期上升, 是造成该站点七月湍流通量异常的主要原因。在此基础上, 该研究也对气团入侵的触发机制进行了讨论。但Van den Broeke等[10]在沿海站Neumayer站的研究却得出了相反的看法, 认为在低气压系统影响下, 云层限制了净长波辐射, 使得近地表大气温差降低, 进而使湍流通量总体变小。

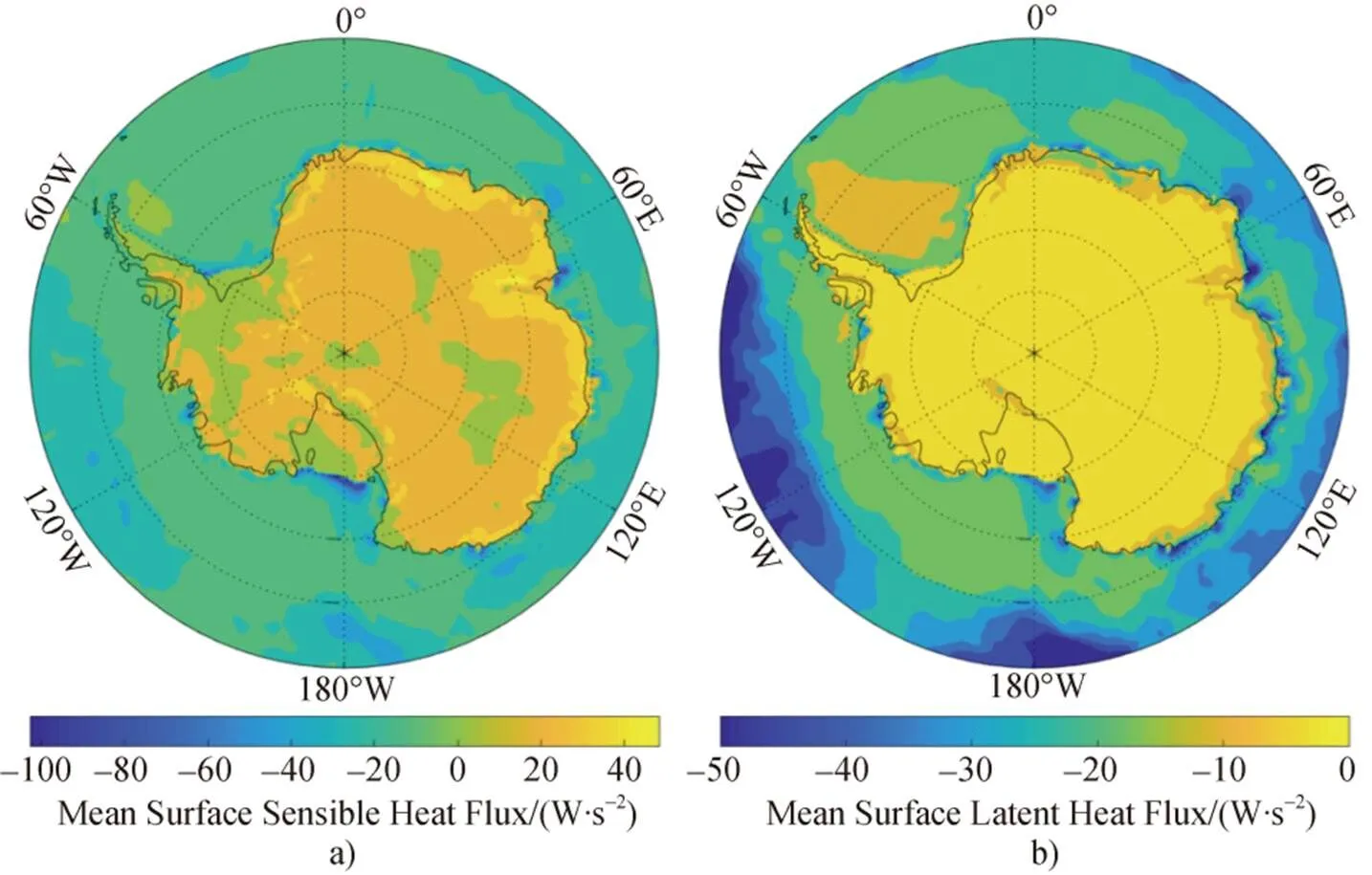
图3 1979—2018年ERA5南极冰盖表面感热与潜热通量平均分布图. a)感热; b)潜热

Fig.3. The average distribution of surface sensible and latent heat fluxes on the Antarctica Ice Sheet which are calculated from ERA5 reanalysis datasets from 1979 to 2018. a) sensible heat; b) latent heat

总体来说, 目前南极湍流通量研究主要依托于模型参数化, 虽然其在模拟湍流要素空间分布方面具有独特的优势, 但是由于涡动实测试验的欠缺, 南极冰盖表面目前湍流参数化方案仍没有较为一致的选择, 其在冰雪表面的相关理论研究仍需要大量的实测资料进行验证。

2.4 南极冰雪热通量研究

构成地表能量平衡方程的各个参数中, 冰雪热通量是衡量近表层雪层与雪表面热量交换的重要指标, 也是控制整个南极冰盖上部热量边界条件的关键。其影响因素主要包括雪层温度梯度、固液气三相态体积占比和雪的微观物理特性(主要是硬度和黏度)等[73-75]。相比于其他的能量分量, 热通量量级通常较小, 所以早期冰雪地表能量平衡研究中其对于融解模拟的贡献往往被忽略[76]。但近年来研究证明, 忽视冰雪热通量的存在可能会使得冰雪融解能量偏高, 高估敏感区域(特别是南极沿岸过渡带)表面物质的损失[67]。所以, 冰雪热通量研究显得尤为重要。

冰雪热通量主要由太阳辐射的渗透和热传导通量组成。短波渗透的能力与介质的密度存在着密切相关[77]。此外, 粒雪的多孔结构和雪层低温也能限制近红外短波辐射的向下渗透, 使其随深度按Bill定律指数衰减[78]。Bintanja等[79]和Favier等[22]就曾基于指数递减的参数化方案, 分别对瑞士Svea站附近雪层、蓝冰区和Dome C附近的短波渗透进行了计算分析, 讨论了其特征。但短波渗透的影响往往与冰雪热传导一起作为冰雪热通量考虑, 少有研究对其进行单独分析。对于雪层下垫面热传导项, 当忽略雪层热平流效应后, 热传导通量为有效热传导系数与近表层雪层温度梯度的积。其中, 有效热传导系数是衡量物体总体导热快慢的指标, 多被视为水平同性, 并且为冰/雪密度或雪温的函数[73-74]。Lei等[80]指出冰雪有效热传导系数的范围可以从新雪的低于0.2 W·K–1·m–1至湿雪或再冻结雪的0.5 W·K–1·m–1, 并由此计算分析了普里兹湾海冰的冰雪热通量特征。风的致密化效应可以通过改变雪的物理结构使得热传导系数更大。Sturm等[81]通过试验对不同环境下雪粒的热传导系数做了研究, 发现风吹雪环境下下垫面的雪粒热传导系数较大, 可达到0.35 W·K–1·m–1。Calonne等[74]也曾使用显微断层图像对多种类型雪的电导率进行了数值模拟, 研究显示当仅考虑通过冰和空气间隙传导热通量时, 有效热传导系数与雪密度呈现线性相关。这类经验性参数化便于计算, 当研究区近表层雪层物理状况较为一致时, 这些方案的误差表现也较好[74,82], 但较不适合于消融区域。

除了直接确定有效热传导系数外, 有效热扩散系数也是计算有效热传导系数的重要手段。利用不同深度雪温随时间类三角函数变化的特性, 有研究提出可以使用不同雪层温度曲线的振幅和位相差来模拟有效热扩散系数[1,83]。此外, 借助类穷举的数学方法将有效热扩散系数代入简化的一维热扩散方程模拟雪温, 与实测雪温进行对比评估, 最终基于误差表现确定系数是另一种可能方法。该方法可以通过选择不同的窗口期, 还原有效热扩散系数在不同时间尺度上的变化。杨堤益[33]在东南极典型下降风区就基于上述方法得出该区域有效热扩散系数为10–8~10–9m2·s–1, 并由此计算求得了冰雪热传导随时间的变化。但精确度很大程度上受限于实测数据的长度和质量, 所以需要进行严格的数据质量控制。

冰雪热通量量级方面一般较小。Carroll[5]计算求得南极点的冰雪热通量年均值为(–0.85± 0.3)W·m–2。在Svea站, Bintanja等[79]得出的冰雪热通量年均值只有0.2 W·m–2。Van den Broeke等[84]则较为完整地对1998—2001年4年11—2月毛德皇后地不同地形下的冰雪热通量进行了计算, 结果表明其内陆高原、下降风区和沿海的站点在研究期间均值也分别只有–3、–2和–2 W·m–2。此外, 晴天条件下, 各站热通量大小相比阴天条件更小。但是, Van den Broeke等[10]研究结果却指出沿海Halley站在风速较小且少云情况下, 雪表温度的强烈下降能使得冰雪热通量量级显著增大。究其原因, 风速量级的大小可能左右了雪表感热通量对辐射亏损的补偿程度, 风速强且较为稳定时(5m·s–1以上), 冰雪热通量的补偿效应则很小, 造成了两者差异。此外, 冰雪热通量能存在较大的日变化。在高原内陆站Dome C站和沿海站Halley站的对比研究中[72], 两站冰雪热通量日变化幅度能达到40 W·m–2左右, 能量收入/支出占比甚至超越了感热通量。这是因为深层雪温波动往往滞后于表层雪温的直接辐射加热/冷却, 且时间变化很小, 10 cm雪温的年变化大约只有表层雪温年变化的四分之三。而在不同冰雪类型的试验中, Datt等[75]基于Maitri站新雪、压实雪和蓝冰的热通量观测, 指出低密度的新雪和蓝冰热通量日变化幅度明显大于高密度压实雪中的状态, 前两者在整个能量平衡日变化中占据着更为重要的部分。其他方面, Ding等[7]地表能量平衡的研究中则显示暖湿气团的影响下, 雪表温显著升高能使向下冰雪热通量增至34 W·m–2左右。

目前南极冰雪热通量的研究中, 观测并不具备较好的时间分辨率, 且模拟研究中热传导通量多使用简化的一维热扩散模型进行展开, 忽略了非传热过程以及热平流等因素的影响, 在敏感区域可能会存在明显的误差。而如何在此类区域中提升模拟水平, 这需要我们今后结合更多雪冰微物理变化观测和理论来开展研究。

3 未来挑战与建议

从国内外南极地表能量平衡研究已有进展和成果可以看出, 目前极地地表能量平衡研究已经取得了一定的进展, 特别是近年来在内陆典型地区的工作, 逐步将该方面的研究自海岸向冰盖高原拓展。但同时, 随着极地预报需求的提升和地球系统模式耦合的需要, 冰/雪-气相互作用过程的重要性愈发凸显。为了解决目前参数化过程中面临的难点, 我们提出如下建议。

1. 在关键气候背景区开展长期观测, 以验证不同方案的适用性。

科学的研究需要资料数量的保障。目前, 法、意合作建设的Concordia站稳定运行至今, 提供了多年的气象要素, 甚至辐射观测数据, 并间有涡动观测试验开展, 在辐射和湍流方面取得了很好的研究成效[11,14]。但在南极, 特别是冬季期间, 仍缺乏长期有效的湍流和热通量实时观测去分析两者要素的季节变化特征, 验证不同参数化方案的适用性, 是目前相关研究中的主要薄弱点。所以开展长期观测, 能为我们拓宽参数化和模拟应用, 揭示更多潜在的地表能量平衡机理。

2. 开展特定的综合观测试验, 研究微观过程。

了解云层与冰雪的微物理性质是探究冰/雪-气相互作用中极为重要的方向。南极现有的辐射和热通量参数化方案虽能得出与实测较为一致的结果, 但由于我们对其微观过程机理认识仍不够透彻, 在研究过程中, 仍会存在一些理论假设上的不足。而如何探究微观理论机制, 这还需要我们今后开展更多云、冰雪微物理过程要素的观测试验, 研究微观过程, 由此建立更完善的理论模型, 并与简化模型比较, 以提高模拟水平。

3. 建设南极气象观测站网, 提升陆面产品的精度。

作为利用资料同化等技术把数值预报产品和观测资料融合起来的“产物”, 陆面产品的提升能为气候监测提供很好的保障, 也能帮助评估和改进气候模式[85]。但目前南极的观测站网仍不完善, 如全球地面辐射基线网络中, 包含的南极站点现只有South Pole、Neumayer和Concordia站等7个站点。相比于偌大的南极大陆, 其观测网格覆盖区域仍不全面, 代表性不足。所以, 建设南极气象观测站网, 提升陆面产品的精度, 也是今后解决参数化难点的突破口之一。

4. 研发适用于极地环境的相关仪器设备, 特别是冰雪的观测设备。

如前建议所述, 科学的观测是研究基础中的基础, 而合适精准的观测设备则是资料质量的保证来源。极地恶劣的自然环境给观测仪器带来了巨大的挑战, 一直是阻碍南极表面认知的最大障碍。目前专门适用于极地环境的相关仪器设备种类仍较少, 且寿命有限。所以积极开展仪器研发工作, 特别是冰雪观测设备的提升是今后南极地表能量平衡研究中最为重要的手段之一。

致谢感谢陈洁、李元和刘子菁在FY-3D卫星资料下载过程中给予的积极帮助。

1 TOWN M S, WALDEN V P. Surface energy budget over the South Pole and turbulent heat fluxes as a function of an empirical bulk Richardson number[J]. Journal of Geophysical Research: Atmospheres, 2009, 114(D22): D22107.

2 VAN AS D, VAN DEN BROEKE M R, HELSEN M M. Strong-wind events and their impact on the near-surface climate at Kohnen Station on the Antarctic Plateau[J]. Antarctic Science, 2007, 19(4): 507-519.

3 杨兴国, 秦大河, 秦翔. 冰川/积雪-大气相互作用研究进展[J]. 冰川冻土, 2012, 34(2): 392-402.

4 WELLER G. Spatial and temporal variations in the south polar surface energy balance[J]. Monthly Weather Review, 1980, 108(12): 2006-2014.

5 CARROLL J J. Long-term means and short-term variability of the surface energy balance components at the South Pole[J]. Journal of Geophysical Research Atmospheres, 1982, 87(C6): 4277.

6 RANDALL D A, CESS R D, BLANCHET J P, et al. Intercomparison and interpretation of surface energy fluxes in atmospheric general circulation models[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D4): 3711-3724.

7 DING M H, YANG D Y, BROEKE M R, et al. The surface energy balance at panda 1 station, princess Elizabeth land: A typical katabatic wind region in east Antarctica[J]. Journal of Geophysical Research: Atmospheres, 2020, 125(3). doi:10.1029/2019jd030378.

8 陈百炼. 一个冰盖近表层能量传输模式的建立及其对南极冰盖热状况的数值模拟研究[D]. 北京: 中国科学院研究生院, 2009.

9 马永锋. 南极中山站至Dome-A考察断面近地层特征参数的研究[D]. 北京: 中国气象科学研究院, 2009.

10 VAN DEN BROEKE M R, KÖNIG-LANGLO G, PICARD G, et al. Surface energy balance, melt and sublimation at Neumayer Station, East Antarctica[J]. Antarctic Science, 2010, 22(1): 87-96.

11 GENTHON C, TOWN M S, SIX D, et al. Meteorological atmospheric boundary layer measurements and ECMWF analyses during summer at Dome C, Antarctica[J]. Journal of Geophysical Research: Atmospheres, 2010, 115(D5): D05104.

12 VAN DEN BROEKE M R, REIJMER C, VAN DE WAL R. Surface radiation balance in Antarctica as measured with automatic weather stations[J]. Journal of Geophysical Research: Atmospheres, 2004, 109(D9): D09103.

13 VAN DEN BROEKE M, VAN AS D, REIJMER C, et al. Sensible heat exchange at the Antarctic snow surface: A study with automatic weather stations[J]. International Journal of Climatology, 2005, 25(8): 1081-1101.

14 VIGNON E, GENTHON C, BARRAL H, et al. Momentum- and heat-flux parametrization at dome C, Antarctica: A sensitivity study[J]. Boundary-Layer Meteorology, 2017, 162(2): 341-367.

15 PARKINSON C L. Aqua: an earth-observing satellite mission to examine water and other climate variables[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(2): 173-183.

16 SCAMBOS T A, FREZZOTTI M, HARAN T, et al. Extent of low-accumulation ‘wind glaze’ areas on the East Antarctic plateau: Implications for continental ice mass balance[J]. Journal of Glaciology, 2012, 58(210): 633-647.

17 SOUVERIJNS N, GOSSART A, DEMUZERE M, et al. A new regional climate model for POLAR-CORDEX: Evaluation of a 30-year hindcast with COSMO-CLM2 over Antarctica[J]. Journal of Geophysical Research: Atmospheres, 2019, 124(3): 1405-1427.

18 BOZKURT D, RONDANELLI R, MARÍN J C, et al. Foehn event triggered by an atmospheric river underlies record-setting temperature along continental Antarctica[J]. Journal of Geophysical Research: Atmospheres, 2018, 123(8): 3871-3892.

19 DAVIN E L, STÖCKLI R, JAEGER E B, et al. COSMO-CLM: a new version of the COSMO-CLM model coupled to the Community Land Model[J]. Climate Dynamics, 2011, 37(9/10): 1889-1907.

20 BROMWICH D H, OTIENO F O, HINES K M, et al. Comprehensive evaluation of polar weather research and forecasting model performance in the Antarctic[J]. Journal of Geophysical Research: Atmospheres, 2013, 118(2): 274-292.

21 BLISS A K, CUFFEY K M, KAVANAUGH J L. Sublimation and surface energy budget of Taylor Glacier, Antarctica[J]. Journal of Glaciology, 2011, 57(204): 684-696.

22 FAVIER V, AGOSTA C, GENTHON C, et al. Modeling the mass and surface heat budgets in a coastal blue ice area of Adelie Land, Antarctica[J]. Journal of Geophysical Research, 2011, 116:F03017. DOI:10.1029/2010JF001939.

23 PAVOLONIS M J, KEY J R, CASSANO J J. A study of the Antarctic surface energy budget using a polar regional atmospheric model forced with satellite-derived cloud properties[J]. Monthly Weather Review, 2004, 132(2): 654-661.

24 REIJMER C H, VAN MEIJGAARD E, VAN DEN BROEKE M R. Evaluation of temperature and wind over Antarctica in a Regional Atmospheric Climate Model using 1 year of automatic weather station data and upper air observations[J]. Journal of Geophysical Research: Atmospheres, 2005, 110(D4): D04103.

25 ROCKEL B, WILL A, HENSE A. The regional climate model COSMO-CLM (CCLM)[J]. Meteorologische Zeitschrift, 2008, 17(4): 347-348.

26 VAN DE BERG W J, VAN DEN BROEKE M R, REIJMER C H, et al. Characteristics of the Antarctic surface mass balance, 1958–2002, using a regional atmospheric climate model[J]. Annals of Glaciology, 2005, 41: 97-104.

27 DETHLOFF K, RINKE A, LEHMANN R, et al. Regional climate model of the Arctic atmosphere[J]. Journal of Geophysical Research: Atmospheres, 1996, 101(D18): 23401-23422.

28 RINKE A, MA Y F, BIAN L G, et al. Evaluation of atmospheric boundary layer-surface process relationships in a regional climate model along an East Antarctic traverse[J]. Journal of Geophysical Research: Atmospheres, 2012, 117(D9). doi:10.1029/2011jd016441.

29 SHU Q, SONG Z, QIAO F. Assessment of sea ice simulations in the CMIP5 models[J]. The Cryosphere, 2015, 9(1): 399-409.

30 BINTANJA R, SEVERIJNS C, HAARSMA R, et al. The future of Antarctica's surface winds simulated by a high-resolution global climate model: 1. Model description and validation[J]. Journal of Geophysical Research: Atmospheres, 2014, 119(12): 7136-7159.

31 YAMANOUCHI T. Variations of incident solar flux and snow albedo on the solar zenith angle and cloud cover, at Mizuho station, Antarctica[J]. Journal of the Meteorological Society of Japan Ser II, 1983, 61(6): 879-893.

32 YAMANOUCHI T, SHUDOU Y S. Trends in cloud amount and radiative fluxes at Syowa Station, Antarctica[J]. Polar Science, 2007, 1(1): 17-23.

33 杨堤益. 东南极冰盖典型下降风区表面能量平衡的参数化研究[D]. 北京: 中国气象科学研究院, 2019.

34 DANA G L, WHARTON R A Jr, DUBAYAH R A. Solar radiation in the Mcmurdo dry valleys, Antarctica[M]//Ecosystem Dynamics in a Polar Desert: the Mcmurdo Dry Valleys, Antarctica. Washington, D. C.: American Geophysical Union, 2013: 39-64.

35 JAKOBS C L, REIJMER C H, KUIPERS MUNNEKE P, et al. Quantifying the snowmelt–albedo feedback at Neumayer Station, East Antarctica[J]. The Cryosphere, 2019, 13(5): 1473-1485.

36 卞林根, 陆龙骅. 拉斯曼丘陵辐射平衡分量的观测研究[J]. 南极研究, 1991, 3(4): 42-53.

37 DING M H, XIAO C D, LI C J, et al. Surface mass balance and its climate significance from the Coast to Dome A, East Antarctica[J]. Science China Earth Sciences, 2015, 58(10): 1787-1797.

38 KING J C, KIRCHGAESSNER A, BEVAN S, et al. The impact of föhn winds on surface energy balance during the 2010-2011 melt season over Larsen C ice shelf, Antarctica[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(22): 12062-12076.

39 DING M H, XIAO C D, YANG Y D, et al. Re-assessment of recent (2008-2013) surface mass balance over Dome Argus, Antarctica[J]. Polar Research, 2016, 35(1): 26133.

40 DING M H, ZHANG T, XIAO C D, et al. Snowdrift effect on snow deposition: Insights from a comparison of a snow pit profile and meteorological observations in east Antarctica[J]. Science China Earth Sciences, 2017, 60(4): 672-685.

41 PARKINSON C L, WASHINGTON W M. A large-scale numerical model of sea ice[J]. Journal of Geophysical Research Atmospheres, 1979, 84(C1): 311.

42 ROESCH A C. Assessment of the land surface scheme in climate models with focus on surface albedo and snow cover[D]. Zurich: Swiss Federal Institute of Technology Zurich, 2000.

43 BRIEGLEB B P, BITZ C M, HUNKE E C, et al. Scientific Description of the Sea ice Component in the Community Climate System Model, version three, 2004. http://www.ccsm.ucar.edu/ models/ccsm3.0/csim.

44 YANG Q H, LIU J P, LEPPÄRANTA M, et al. Albedo of coastal landfast sea ice in Prydz Bay, Antarctica: Observations and parameterization[J]. Advances in Atmospheric Sciences, 2016, 33(5): 535-543.

45 WISCOMBE W J, WARREN S G. A model for the spectral albedo of snow. I: Pure snow[J]. Journal of the Atmospheric Sciences, 1980, 37(12): 2712-2733.

46 BUSETTO M, LANCONELLI C, MAZZOLA M, et al. Parameterization of clear sky effective emissivity under surface-based temperature inversion at Dome C and South Pole, Antarctica[J]. Antarctic Science, 2013, 25(5): 697-710.

47 秦听, 魏立新, 李珵. 我国南极科考站附近气旋的特征分析[J]. 海洋学报(中文版), 2017, 39(5): 44-60.

48 VIGNON E, HOURDIN F, GENTHON C, et al. Modeling the dynamics of the atmospheric boundary layer over the Antarctic plateau with a general circulation model[J]. Journal of Advances in Modeling Earth Systems, 2018, 10(1): 98-125.

49 DING M H, AGRAWAL A, HEIL P, et al. Surface energy balance on the Antarctic plateau as measured with an automatic weather station during 2014[J]. Advances in Polar Science, 2019, 30(2): 93-105.

50 DILLEY A C, O'BRIEN D M. Estimating downward clear sky long-wave irradiance at the surface from screen temperature and precipitable water[J]. Quarterly Journal of the Royal Meteorological Society, 1998, 124(549): 1391-1401.

51 HUNT H W, FOUNTAIN A G, DORAN P T, et al. A dynamic physical model for soil temperature and water in Taylor Valley, Antarctica[J]. Antarctic Science, 2010, 22(4): 419-434.

52 OHMURA A. Physical basis for the temperature-based melt-index method[J]. Journal of Applied Meteorology, 2001, 40(4): 753-761.

53 ZHOU Y P, KRATZ D P, WILBER A C, et al. An improved algorithm for retrieving surface downwelling longwave radiation from satellite measurements[J]. Journal of Geophysical Research Atmospheres, 2007, 112(D15): D15102.

54 KONZELMANN T, VAN DE WAL R, GREUELL W, et al. Parameterization of global and longwave incoming radiation for the Greenland Ice Sheet[J]. Global and Planetary Change, 1994, 9(1-2): 143-164.

55 LISTON G E, ELDER K. A meteorological distribution system for high-resolution terrestrial modeling (MicroMet)[J]. Journal of Hydrometeorology, 2006, 7(2): 217-234.

56 YU S S, ZHANG H L, XIN X Z, et al. A method for calculating global downwelling longwave radiation using geostationary and polar-orbiting satellite observations[C]//2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Beijing: IEEE, 2016.

57 GUBLER S, GRUBER S, PURVES R S. Uncertainties of parameterized surface downward clear-sky shortwave and all-sky longwave radiation[J]. Atmospheric Chemistry and Physics, 2012, 12(11): 5077-5098.

58 SVERDRUP H U. The eddy conductivity of the air over a smooth snow field [J]. Geofysiske Publikasjoner, 1936, 11:5-69.

59 KING J C, ANDERSON P S. Heat and water vapour fluxes and scalar roughness lengths over an Antarctic ice shelf[J]. Boundary-Layer Meteorology, 1994, 69(1/2): 101-121.

60 LETTAU H H. Wind and temperature profile prediction for diabatic surface layers including strong inversion cases[J]. Boundary-Layer Meteorology, 1979, 17(4): 443-464.

61 GRACHEV A A, ANDREAS E L, FAIRALL C W, et al. SHEBA flux-profile relationships in the stable atmospheric boundary layer[J]. Boundary-Layer Meteorology, 2007, 124(3): 315-333.

62 LOUIS J F. A parametric model of vertical eddy fluxes in the atmosphere[J]. Boundary-Layer Meteorology, 1979, 17(2): 187-202.

63 ANDREAS E L. Parameterizing scalar transfer over snow and ice: A review[J]. Journal of Hydrometeorology, 2002, 3(4): 417-432.

64 BELJAARS A C M, HOLTSLAG A A M. Flux parameterization over land surfaces for atmospheric models[J]. Journal of Applied Meteorology, 1991, 30(3): 327-341.

65 周德刚, 黄刚, 马耀明. 中国西北干旱区戈壁下垫面夏季的热力输送[J]. 大气科学学报, 2012, 35(5): 541-549.

66 VAN AS D, VAN DEN BROEKE M R, HELSEN M M. Structure and dynamics of the summertime atmospheric boundary layer over the Antarctic Plateau: 1. Measurements and model validation[J]. Journal of Geophysical Research Atmospheres, 2006, 111(D7): D07102.

67 INOUE J. Surface drag over the snow surface of the Antarctic Plateau: 1. Factors controlling surface drag over the katabatic wind region[J]. Journal of Geophysical Research Atmospheres, 1989, 94(D2): 2207.

68 ANDREAS E L. A theory for the scalar roughness and the scalar transfer coefficients over snow and sea ice[J]. Boundary-Layer Meteorology, 1987, 38(1/2): 159-184.

69 VAN DEN BROEKE M R, VAN LIPZIG N P M. Factors controlling the near-surface wind field in Antarctica[J]. Monthly Weather Review, 2003, 131(4): 733-743.

70 THIERY W, GORODETSKAYA I V, BINTANJA R, et al. Surface and snowdrift sublimation at Princess Elisabeth station, East Antarctica[J]. The Cryosphere, 2012, 6(4): 841-857.

71 BINTANJA R, VAN DEN BROEKE M R. The surface energy balance of Antarctic snow and blue ice[J]. Journal of Applied Meteorology, 1995, 34(4): 902-926.

72 KING J C, ARGENTINI S A, ANDERSON P S. Contrasts between the summertime surface energy balance and boundary layer structure at Dome C and Halley stations, Antarctica[J]. Journal of Geophysical Research Atmospheres, 2006, 111(D2): D02105.

73 AGGARWAL R. New density-based thermal conductivity equation for snow[J]. Defence Science Journal, 2009, 59(2): 126-130.

74 CALONNE N, FLIN F, MORIN S, et al. Numerical and experimental investigations of the effective thermal conductivity of snow[J]. Geophysical Research Letters, 2011, 38(23). DOI:10.1029/2011gl049234.

75 DATT P, GUSAIN H S, DAS R K. Measurements of net subsurface heat flux in snow and ice media in Dronning Maud Land, Antarctica[J]. Journal of the Geological Society of India, 2015, 86(5): 613-619.

76 BROCK B W, WILLIS I C, SHARP M J. Measurement and parameterization of albedo variations at Haut Glacier d’Arolla, Switzerland[J]. Journal of Glaciology, 2000, 46(155): 675-688.

77 BOHREN C F, BARKSTROM B R. Theory of the optical properties of snow[J]. Journal of Geophysical Research Atmospheres, 1974, 79(30): 4527-4535.

78 BRANDT R E, WARREN S G. Solar-heating rates and temperature profiles in Antarctic snow and ice[J]. Journal of Glaciology, 1993, 39(131): 99-110.

79 BINTANJA R, JONSSON S, KNAP W H. The annual cycle of the surface energy balance of Antarctic blue ice[J]. Journal of Geophysical Research: Atmospheres, 1997, 102(D2): 1867-1881.

80 LEI R B, LI Z J, CHENG B, et al. Annual cycle of landfast sea ice in Prydz Bay, east Antarctica[J]. Journal of Geophysical Research Atmospheres, 2010, 115(C2): C02006.

81 STURM M, HOLMGREN J, KÖNIG M, et al. The thermal conductivity of seasonal snow[J]. Journal of Glaciology, 1997, 43(143): 26-41.

82 YEN Y C. Review of Thermal Properties of Snow, Ice and Sea Ice: Crrel Report 81-10[R]. Hanover: U.S. Army Cold Regions Research and Engineering Laboratory, 1981.

83 SERGIENKO O V, MACAYEAL D R, THOM J E. Reconstruction of snow/firn thermal diffusivities from observed temperature variation: Application to iceberg C16, Ross Sea, Antarctica, 2004–07[J]. Annals of Glaciology, 2008, 49: 91-95.

84 VAN DEN BROEKE M, REIJMER C, VAN AS D, et al. Daily cycle of the surface energy balance in Antarctica and the influence of clouds[J]. International Journal of Climatology, 2006, 26(12): 1587-1605.

85 赵天保, 符淙斌, 柯宗建, 等. 全球大气再分析资料的研究现状与进展[J]. 地球科学进展, 2010, 25(3): 242-254.

ADVANCES IN THE STUDY OF SURFACE ENERGY BALANCE ON THE ANTARCTIC ICE SHEET

Yang Diyi1,2, Ding Minghu2, Zou Xiaowei2

(1Haining Meteorological Bureau, Haining 314400, China;2Institute of Tibetan Plateau and Polar Meteorology, Chinese Academy of Meteorological Sciences, Beijing 100081, China)

The research of surface energy balance on snow/ice on Antarctica ice sheet is the basis for coupling the cryosphere, atmosphere and hydrosphere processes, which is of great significance for understanding the process of surface mass balance of the ice sheet and enhancing the level of polar weather and climate prediction. With the improvement of polar observations in recent years, great progress has been made in our understanding of the surface energy balance of the Antarctic ice sheet, especially in albedo parameterization and derivation of the effective thermal conductivity. However, because of the vast area and variable weather conditions of Antarctica, results from most of the existing studies are only applicable to local environments which limit our ability to model and forecast. Therefore, conducting scientific experiments in key climate regions, developing sensors for the special polar environment and a basic network of meteorological stations can deepen our understanding of ice/snow–air interactions, and contribute towards further improvements of parametric coupling schemes in numerical models.

surface energy balance,research advance, Antarctic ice sheet

2020年3月收到来稿, 2020年5月收到修改稿

自然科学基金(41771064、4194100049)和中国气象科学研究院基本科研业务费(2019Z005)资助

杨堤益, 男, 1993年生。助理工程师, 主要从事冰气相互作用方面研究。E-mail: yangdiyi@foxmail.com

丁明虎, E-mail: dingminghu@foxmail.com

10. 13679/j.jdyj.20200014