三角闸门顶枢结构计算分析

杨铎，顾磊，胡友安，姜胜先

（1.安徽省交通勘察设计院有限公司，安徽 合肥 230011；2.河海大学机电工程学院，江苏 常州 213022）

1 研究背景

三角闸门是由左、右各一扇绕竖轴旋转进行启闭的扇形或三角形门体构成的船闸闸门，其凭借可承受双向水头压力且在水头小于0.5 m的情况下动水启闭等众多独特优点而得以广泛运用[1]，图1为实际工程运用图。在三角闸门正常的运行过程中，顶枢与底枢起主要承重与支承作用，运用SolidWorks软件对顶枢进行建模与装配，结构装配图如图2所示。

三角闸门中底枢因工作条件恶劣而对之有较多研究，如赵新泽等[2]、刘浩等[3]对底枢进行Workbench有限元仿真，为工程实际提供参考依据，赵新泽等[4]基于底枢摩擦副失效形式提出了降低接触应力的措施。针对顶枢易于在频繁运行的重载低速条件下发生故障，李然[5]通过模拟顶枢轴润滑不良情况为实时状态检修提供指导价值；在顶枢结构方面，林燕梅[6]结合具体工程阐述其结构设计，但在顶枢结构强度方面的研究较为欠缺。对此，本文利用Workbench对顶枢进行非线性有限元分析，并与理论计算结果进行对比，为顶枢在实际工程中的设计与运用提供参考与借鉴。

图1 三角闸门实物图Fig.1 Object picture of the triangular gate

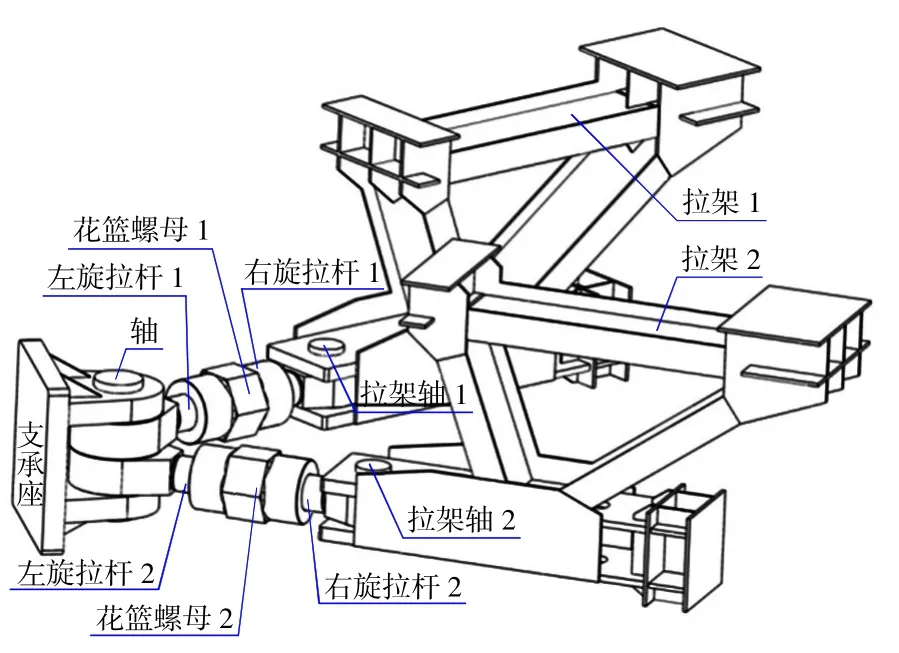
图2 顶枢结构装配图Fig.2 Assembly graphic of the structure of top pintle

2 支座反力求解

本文以引江济淮工程合裕线上的三角闸门为工程背景展开研究，其中心角为70°，主弧半径R=18.3 m，面板高度14.86 m。面板、主梁等采用Shell181单元模拟，刚架结构、水平次梁等采用Beam188单元模拟。闸门材料为Q355B，其弹性模量E=2.06×1011Pa，泊松比μ=0.3，密度ρ=7 850 kg/m3。

给定闸门如下约束：底枢水平方向和竖直方向位移约束（X、Y、Z），顶枢和启闭点水平方向位移约束（X、Y）。结合表1中4种不同设计水位组合，对上述有限元模型在不同组合工况下进行求解以提取闸门顶枢处拉力[7]，并将结果进行汇总。

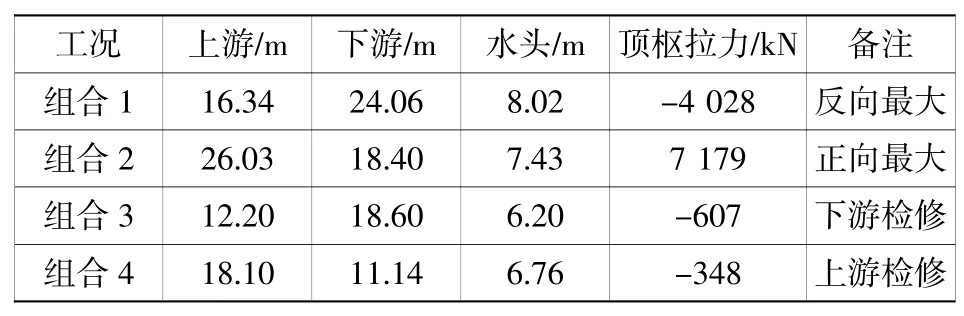
表1 不同设计水位下顶枢拉力Table 1 Top pintle tension under different design water levels

3 非线性接触分析

接触状态指两物体表面彼此接触且互切，此类问题属于状态变化的高度非线性行为。Workbench为达到实际接触体彼此互不穿透的目的，提供接触方程——纯粹罚函数法、增广Lagrange法、MPC法等进行强制接触协调，结合本文研究对象——顶枢的实际接触情况，主要采用纯粹罚函数法和增广Lagrange法[8]。Workbench中5种接触类型及特点如表2所示。

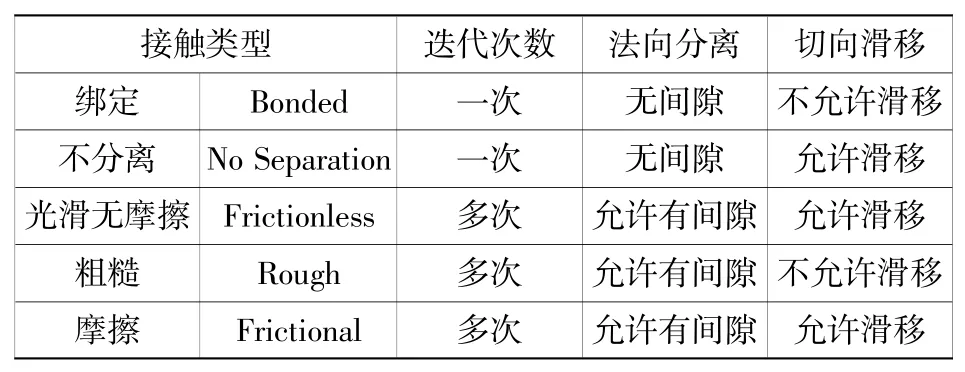
表2 Workbench中接触类型及特点Table 2 Contact types and characteristics in Workbench

基于表2中接触类型与特点，考虑顶枢中各部件的实际接触情况，将左旋拉杆1与轴、左旋拉杆2与轴之间的接触类型设置为Frictional（摩擦），其余部件间接触类型设置为Bonded（绑定）。

3.1 罚函数法

检测接触面是否发生穿透会在系统每进行一次子步计算时进行：若未穿透则不处理，否则在接触面上引入法向接触力FN：

式中：KN为法向接触刚度；x为穿透深度。

3.2 增广Lagrange法

为减弱计算过程中对接触刚性变化的敏感性，基于罚函数法在法向接触力上增加额外接触力λ。此时，法向接触力FN变为：

4 平面计算与有限元结果对比分析

4.1 顶枢有限元模型与参数

基于SolidWorks的顶枢装配模型，将其另存为X_T文件并导入Workbench中[9]，根据各部件实际材料赋值相应材料参数并进行网格划分。图3为顶枢有限元模型。

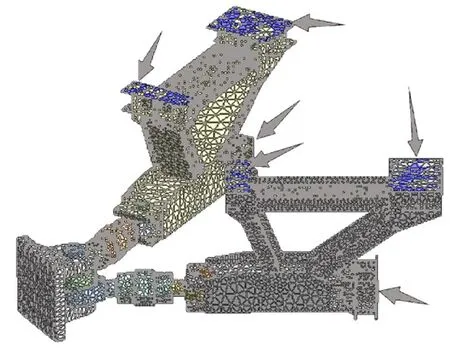
图3 顶枢有限元模型Fig.3 Finite element model of the top pintle

根据表1中顶枢拉力求解结果，选取最不利情况下顶枢拉力进行以下分析，即：选取组合2工况下的顶枢拉力，并在支承座竖直面板上施加水平拉力F=7 179 kN。同时，考虑顶枢实际受约束情况，在拉架1和拉架2的水平面与竖直面处施加Fixed约束，具体位置如图3中箭头所指处。

4.2 理论计算与有限元结果

基于上述非线性接触分析理论，运用Workbench进行有限元求解，并对相关部件根据材料力学理论计算原理进行求解，将相关结果进行汇总如表3所示。在表3中，偏差[10]指理论计算与有限元结果平均值之间的偏差。

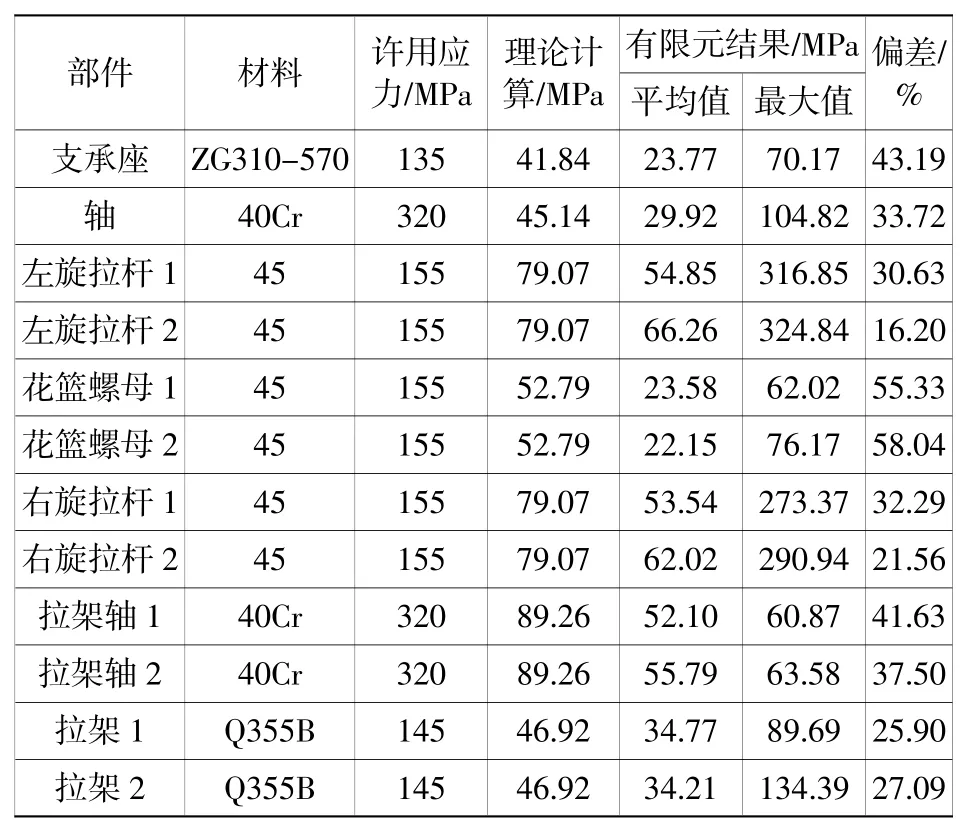
表3 顶枢各部件理论计算与有限元结果对比Table 3 Comparison of theoretical calculation and finite element results of top pintle components

4.3 结果对比分析

分析表3数据可知：顶枢各部件理论计算结果高于有限元结果的平均值，偏差最大值与最小值分别达16.20%和58.04%，分别位于左旋拉杆2和花篮螺母2处，造成上述偏差较大的原因有二：第一，理论计算时将各部件彼此孤立，故未能考虑结构整体的相互协调作用；第二，理论计算时无法将各部件之间非线性接触行为考虑其中，这亦是产生上述偏差的重要原因。

在表3中，还需指出：左旋拉杆1、2和右旋拉杆1、2有限元结果的最大值分别达316.85 MPa、324.84 MPa、273.37 MPa和290.94 MPa，远超其许用应力155 MPa，但除此之外其余部件的有限元结果最大值均在各自材料的许用应力范围之内。为进一步探究左、右旋拉杆1、2产生上述情况的原因，从Workbench有限元结果中提取相应应力云图，如图4所示。

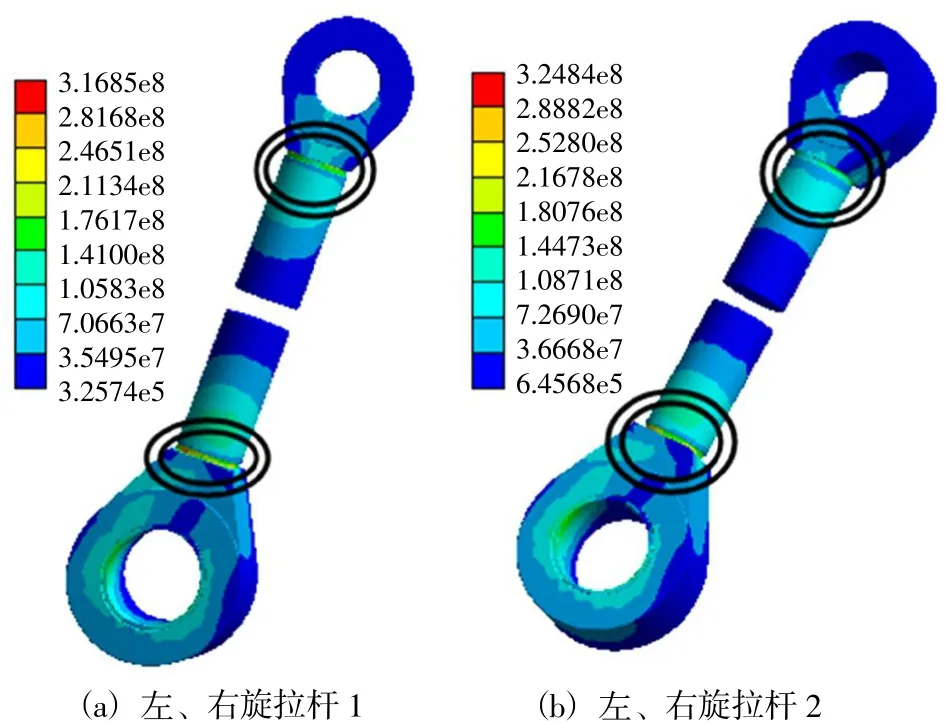
图4 应力云图（Pa）Fig.4 Stress nephogram(Pa)

图4 直观体现了在左、右旋拉杆1、2处存在明显应力集中现象，具体位于图中双圆圈处，但其均属于接触应力，在塑性变形后会迅速恢复正常[11-12]，且旋拉杆整体平均应力在71.68 MPa左右，远低于许用应力155 MPa，故上述应力集中现象对结构整体无太大影响。为保险起见，可对应力集中处结构稍加调整，如增大倒角半径等以缓减应力集中现象，确保顶枢结构安全可靠。

基于上述分析可知：理论计算结果高于有限元结果的平均值，体现出理论计算更具安全性，适合于顶枢结构的理论设计，且效率更高，但需重视旋拉杆结构的合理性，确保闸门安全可靠运行；有限元结果贴合于工程实际，对其更具指导意义。上述结论为生产实际中理论计算与有限元方法的选择提供了重要参考依据。

5 结语

本文运用Workbench软件对顶枢进行非线性有限元分析，并与理论计算结果进行对比，结论如下：

1）顶枢各部件理论计算结果与有限元结果偏差较高，这是由于理论计算时无法考虑结构整体的相互协调性与各部件间非线性接触行为所致。

2）左、右旋拉杆1、2处存在明显应力集中现象，但其属于接触应力，在塑性变形后会迅速恢复正常，对结构整体无较大损害。

3）理论计算对顶枢结构的设计具有较高的运用价值，结构设计高效且安全；Workbench有限元分析与工程实际更贴合，可为实际生产提供指导意义。

上述结论为生产实际中理论计算与有限元方法的选择提供了重要参考依据。