偏压作用下各向异性深埋软岩隧道的地应力反演

吴帮标，张浩东，于长一，刘爱民

（1.天津大学建筑工程学院，天津 300354；2.中交天津港湾工程研究院有限公司，天津 300222；3.中交第一航务工程局有限公司，天津 300461；4.港口岩土工程技术交通行业重点实验室，天津300222；5.天津市港口岩土工程技术重点实验室，天津 300222）

0 引言

初始应力场是隧道变形与失稳的主要影响因素，也是科学指导隧道开挖与支护的前提条件。在工程当中，可用于指导现场施工的初始应力场可视为忽略时间因素（地质年代）的相对稳定应力场，所以直接测量所得的地应力是具有指导意义的。在早期的工程当中，利用某种方法在地下进行实地测量，所得的实测资料，是唯一可供应用的初始地应力值。然而受成本和工期的限制，少数测点又难以满足工程需要。考虑到在工程中运用少数测点的应力值进行反演，提供一个相对准确的初始应力场，便成为解决工程稳定性问题的一个有效方法[1]。

目前，地应力场的反演方法主要有位移反分析法[2]和应力反分析法[3]。位移反演分析法仅仅适用于地形地貌较简单，地层分布较为单一的工况。而应力反演分析法又可分为两类，第一类属于定性分析的范畴，例如将初始地应力场划分为自重应力场、构造应力场、温度应力场和地磁应力场等。产生的方法有边界荷载调整法、侧压系数法、应力函数法[4-6]等方法。第二类方法则是定量分析，目前采用的分析方法有：多元线性回归分析法、神经网络法[7-8]等。上述各种方法都或多或少存在着计算精度和收敛速度方面的问题，难以准确地指导设计和施工。

为此，本文结合云南某单线铁路各向异性软岩隧道，在定性分析的基础上，采用griddata函数插值法对有限元模拟软件所得的地应力场进行修正。本文主要包括以下几个部分：首先介绍了工程概况以及研究背景；接着建立了有限元模型对地层的各项参数进行标定；随之用模拟软件模拟地层结构，初步得到监测断面的地应力场；然后利用griddata函数对数值计算结果进行修正，最后将结果与实测值进行对比分析，验证griddata函数法修正结果的准确性。

1 工程概况

云南某铁路隧道进口里程DK405+615，出口里程DK415+124，全长9 509 m，施工隧道最大埋深711 m。

隧道整体为构造剥蚀、侵蚀中低山地貌。为了更好地对软岩隧道的地应力分布进行研究，本文选取的研究对象为隧道里程DK414+647处监测断面，此断面处围岩主要为侏罗纪和平乡组（J2h）、小红桥组（J2x）泥岩、砂岩夹页岩、砾岩等，主要岩性的岩石坚硬程度划分为软岩（5 MPa≤Rc≤15 MPa），受地质构造影响较重或严重，节理较发育或发育，具有典型的软岩特征。监测断面围岩部分呈块（石）碎（石）状镶嵌结构的部分，接近隧道轮廓线部分岩体表现为较破碎至破碎，呈角砾碎石状松散结构。

在隧道开挖后，局部发生软岩大变形，易发生坍塌、掉块、侧向挤入，造成很大的安全隐患。为了预防隧道施工中产生的高风险，在开挖后迅速于监测断面布置压力盒，用于监测围岩压力的变化情况，充分对该类隧道进行围岩压力和支护的应力量测，此时测得的围岩压力就等于隧道临空区最边缘的应力，其变化曲线可以理解为断面开挖后应力重分布的变化过程，此应力值将作为地应力反演的一个重要依据。因此，选择围岩压力时程曲线20 d之后压力值趋于稳定的数值作为围岩最终压力值，图1为DK414+647围岩压力值横断面分布图。

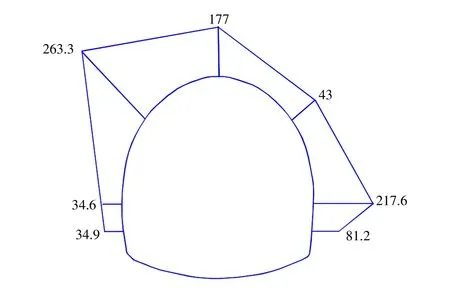
图1 围岩压力值横断面分布图（kPa）Fig.1 Cross-section distribution map of surrounding rock pressure value(kPa)

2 有限元模型及参数标定

本文采用有限元软件进行数值模拟分析，根据工程前期所得的测点围岩压力，结合数值模拟实验验证，分析地应力分布的影响因素，对局部断面的地应力场进行反演。

2.1 几何模型

根据该隧道的地质报告，隧道走向与最大水平主应力的走向之间的夹角始终恒定，即沿着隧道走向，任意断面的地应力情况均相同，同时二维模型假设荷载沿着隧道轴向均匀分布，故将三维的地应力问题简化为二维模型进行计算。为消除边界影响[9]，二维模型选取隧道横断面内以隧洞为中心半径大于3倍洞径的方形区域，分析范围为100 m×100 m；开挖隧洞为椭圆形，最高处9.38 m，最宽处7.30 m。计算模型总共划分单元数为6 878个，结点数为6 997个。

2.2 本构参数

本文主要研究初始地应力的分布，不涉及开挖变形等的讨论，因此本构模型选取摩尔库伦模型；考虑到开挖后的应力松弛，根据极限平衡自稳拱原理[10]，可计算出隧道开挖后自稳拱的最大高度作为拉应力区的半径最大值，故近似的将在开挖分析步中调整隧洞轮廓线向外延伸2 m的范围内的围岩参数。受开挖扰动影响，隧道周围物理参数开挖前后有差异，将沿隧道径向取出的土样分段进行室内实验，将土样2 m之内和之外的参数进行分别记录，最终确定的开挖前后围岩各项物理力学参数如表1所示。

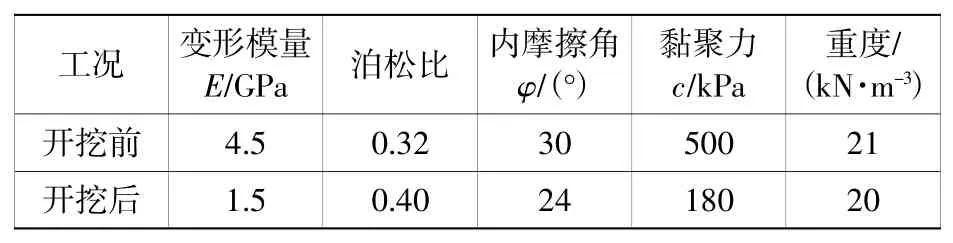
表1 围岩物理力学参数Table 1 Physical and mechanical parameters of surrounding rock

2.3 地层参数标定

依据现场地质勘查资料，结合王福和[11]在实际偏压隧道工程中的模拟结果进行分析，该监测断面上部受到偏压的影响，且其围岩类别多为泥质页岩，故洞周围岩的应力值受到上部偏压和各向异性的影响，因此本文通过数值模拟实验的边界荷载调整法来还原地应力场，在模型上部的1/4处、1/2处、3/4处分别施加偏压荷载，观察其应力集中区域；各向异性设置为正交各向异性，偏转角度分为30°、35°、40°、45°、50°、55°、60°7种情况进行实验（图2），得出最符合实际情况的边界荷载及围岩材料方向。

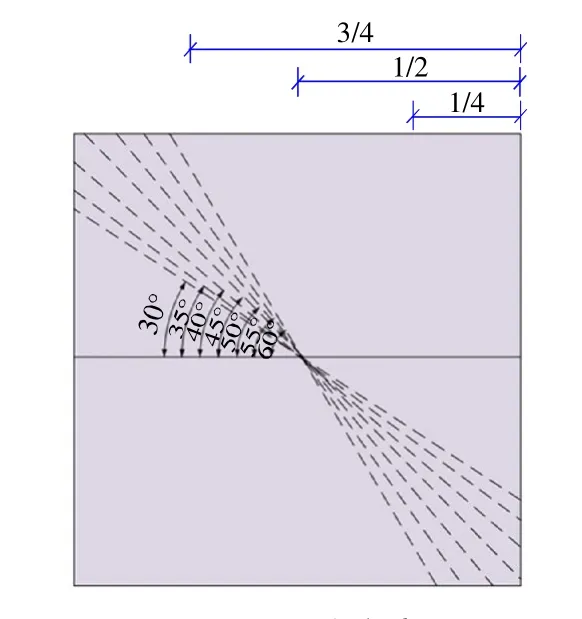
图2 实验方案Fig.2 Experimental program

2.4 数值模拟工况

本次模拟的目的是还原隧道开挖后监测断面的应力值，因此数值模拟的第一步是还原开挖之前的真实应力场，并且进行地应力平衡，第二步进行隧洞开挖，计算完成后导出模型中对应监测点的应力值，并与实测值进行对比。

2.5 反演边界条件

根据模拟实验结果，计划在进行反演时对模型偏右3/4上边界施加偏压荷载，对整个模型上边界施加上部土体压强，整个模型施加自身重力，同时设置各向异性材料方向为35°（图3），模型左右边界限制X方向上的位移，下部边界限制X、Y两个方向上的位移。

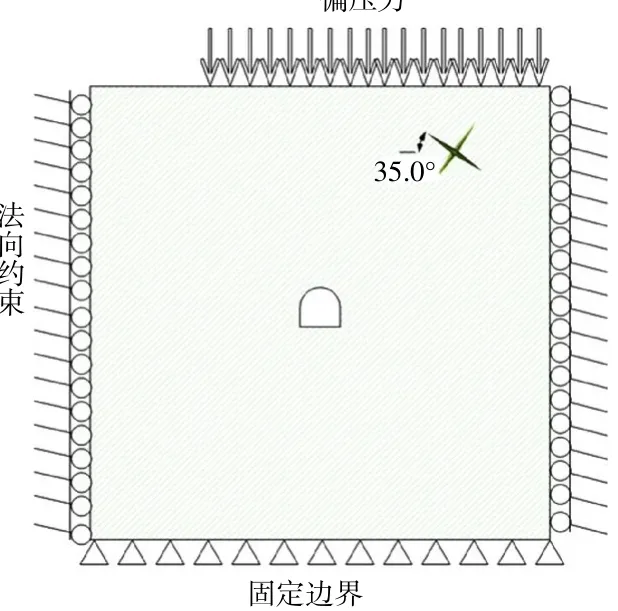
图3 边界条件Fig.3 Boundary conditions

3 地应力场反演结果

3.1 地应力场初步反演结果

在建立有限元模型的基础上，通过模拟实验得到监测断面的偏压与各向异性情况，并计算得到监测点处最接近实测值的应力云图，如图4所示。

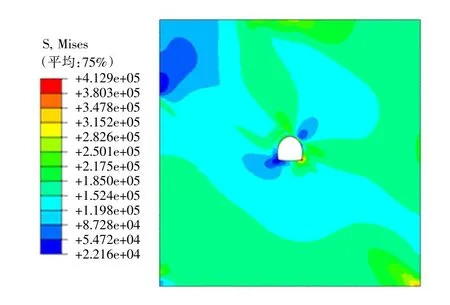
图4 开挖后监测断面应力云图Fig.4 Monitoring section stress cloud map after excavation

从图中可以看出，通过数值模拟计算出的应力值与实测值较为接近，同样为左拱腰和右拱脚出现应力集中，应力水平的倾向性较为明显，符合现场实测资料。由于数值模拟中边界条件与实际工程中的情况并不相同，且工程中的岩性更为复杂，而使在右拱腰与左拱脚出处应力值有较大的出入，但是应力集中与应力较弱区域的分布情况与实际值是相似的。

尽管模拟出的结果在分布和量值上与实测值相接近，但洞周围岩的压力值与实测值之间仍存在着不小的出入，此种误差的存在，使模拟结果难以作为指导支护施作的主要依据。因此，采用griddata函数作为修正函数结合现场实测值对模拟结果进行修正，使反演值更加接近实际地应力值。

3.2 采用griddata函数法修正地应力场

为了保证地应力的反演结果尽可能的与实测值接近，故在数值模拟的基础上，结合有限的实测点应力值，运用Matlab中的griddata函数进行修正。

griddata函数可以将位于同一空间坐标系下的散点插值为规则格网，提供了以下4种方法：线性内插法、三次多项式内插法、最邻近点内插法和Matlab自带的一种圆滑插值法，可方便地实现结合临近离散点分布特征的光滑曲面拟合。其程序实现伪代码如下：

[xi，yi]=meshgrid（min（x）∶dx∶max（x），min（y）∶dy∶max（y）），%，生成规格化格网；

[xi，yi，zi]=griddata（x，y，z，xi，yi，′method′），%，应力值平面拟合；

zi=griddata（x，y，z，xi，yi，′method′），%，求待拟合点的应力值；

surf（xi，yi，zi），%，应力云图。

从数值模拟的结果分析，地应力场的应力集中区域与实测相对符合，但是隧道断面边缘的应力值在部分区域则有些出入，而此处反演有误差的部分恰好具有实测点的数值，因此，将应力松弛区域以外的模拟应力值与区域内的实测值运用griddata函数再次进行插值计算，可得到与实测值更为接近的地应力场。

3.3 采用griddata函数法修正结果

结合数值模拟计算，采用griddata函数圆滑插值法对断面地应力场进行修正的结果见表2。

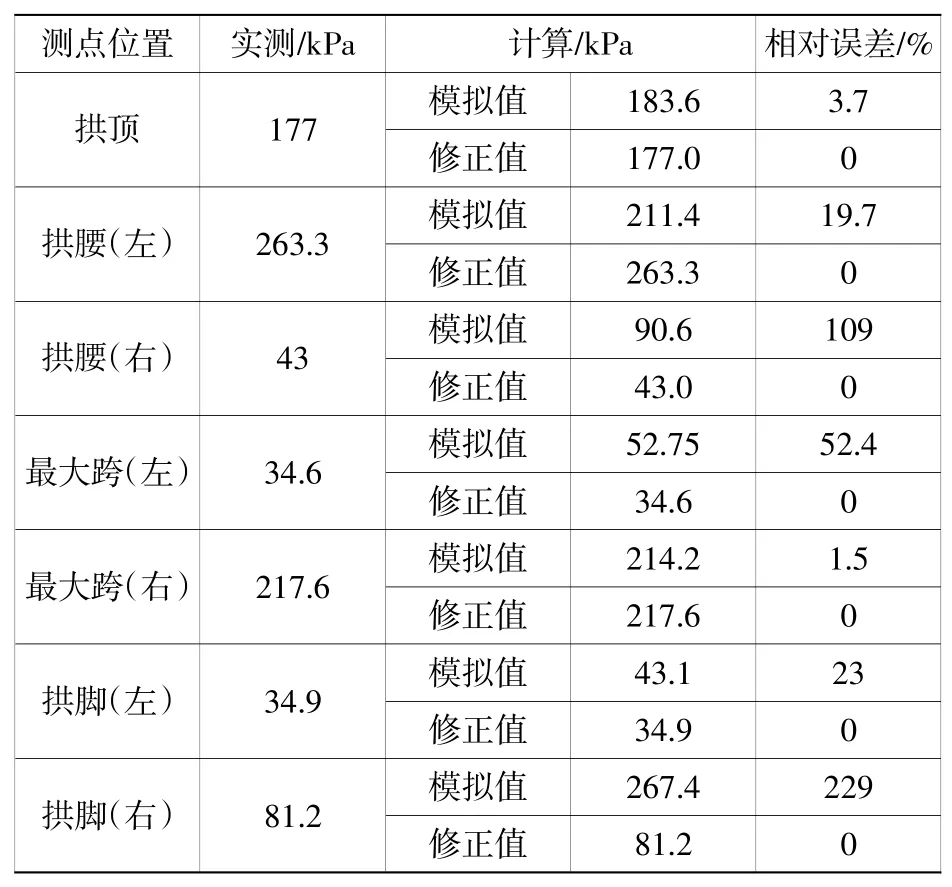
表2 反演应力值结果对比Table 2 Comparison of inversion stress values

从反演结果中可以看到，在隧道左拱腰处与右侧墙脚处同样出现应力集中，与实测和数值模拟计算两种方法相比，分布区域均类似，偏压荷载与各向异性影响明显，数值模拟方法中所得的结论再次得到验证。同时，反演结果的洞周测点处围岩应力数值与实测值完全相同，显然在地应力反演的计算精度上，griddata函数有明显的优势。

4 反演应力值对比分析

将用griddata函数法修正后的结果和仅用数值模拟方法计算所得的围岩压力与实测值进行比较，均发现在左拱腰与右拱脚处有明显的应力集中现象，在右拱腰与左拱脚处的应力相对较小，应力集中与应力较弱的区域分布均相同。

从表2的对比结果可以看出，数值模拟软件的模拟误差最大为229%，误差较大，没有参考价值；右拱腰处的误差较大，但是应力集中区域的分布类似，可以认为是材料参数与边界条件引起的误差；其余点的相对误差主体在20%以下，超出30%的点为1个。而在地应力测量阶段，测量方法本身便会导致测量结果的误差，据国内外的统计资料所示，初始地应力值的测量结果误差允许达到25%～30%[12]，故而认为数值模拟方法所得的地应力值与实测值基本符合。

由于插值计算法多为数学模型，难以确定其误差，故其计算精度可用内外符合精度表示，内符合精度为拟合点与拟合曲线的差值，外符合精度为核检点与拟合值的插值。griddata函数拟合曲面通过各拟合点，故拟合点的内符合精度为0，据相关学者研究[13]，griddata函数插值点的残差与外符合精度相较于多面函数有很大的提高，与最小二乘法相比也具有相当的精度。可以认为griddata函数插值法高度的还原了工程实际中的地应力值。本文分析的地形中围岩情况较为复杂，有明显的软岩性质和各向异性，采用griddata函数修正法能够很好地模拟出隧道中应力集中的区域，表现出其地质构造对地应力分布的影响。

5 结语

针对各向异性的深埋软岩隧道地应力反演问题，本文首次提出采用griddata函数对模拟软件得到的地应力进行修正，并结合有限元数值模拟试验对该问题进行了深入研究，结果如下：

1）本文利用数值模拟软件对云南某软岩隧道某监测断面进行数值模拟，尽管模型边界条件与岩石物理力学参数并不能与实际完全一致，从而使部分结果存在误差，但是通过试算法仍然模拟出了与开挖断面的围岩压力值相近的结果，并且能供实际工程参考。

2）griddata函数修正的计算结果具有高精度。本文采用基于griddata函数的函数修正法，得到了其程序实现方法并绘出了计算结果云图。通过对比分析，griddata函数修正计算结果应力集中区域与数值模拟结果相似，应力值与实测值高度相似，证明griddata函数具有相当高的计算精度，结合现场实测值，能够为现场施工做出有效的指导。