失效卫星姿态接管的并行学习合作博弈控制
2021-03-27韩楠罗建军马卫华
韩楠,罗建军,马卫华,*
1. 西北工业大学 航天学院,西安 710072 2. 西北工业大学 航天飞行动力技术重点实验室,西安 710072
接管控制技术为空间失效卫星有效载荷的再利用提供了新途径。微小卫星具有研制成本低、研制周期短、发射方便的优点[1],是实施失效卫星姿态接管控制的新思路。近年来,针对空间资源再利用和新卫星在轨组装任务,以凤凰计划、iBOSS计划为代表的模块化卫星项目被陆续提出。其所构想的辅助连接装置及标准化接口[2-4],可满足模块化卫星之间及模块化卫星与失效卫星之间的连接需求,是实现微小卫星与失效卫星相互连接的有效途径。当多颗微小卫星与失效卫星互连形成组合体后,便可通过互相协同为失效卫星的姿态运动接管和操作提供控制。
由于微小卫星与失效卫星所形成的组合体可近似视为一刚性航天器,因此可利用传统航天器姿态控制及控制分配方法计算各颗微小卫星的控制力矩[5-8]。然而,这种方法需要中央处理单元进行微小卫星控制力矩的计算,当微小卫星数量过多时,中央处理单元会面临较大的计算负担。为了将计算负担分散在各颗微小卫星之间,文献[9]研究了微小卫星的分布式控制分配问题,然而,微小卫星的控制约束没有得到考虑。
微分博弈研究了多个体的决策互动问题,其中各个体通过局部目标函数的优化获得控制策略[10-11],这为通过多颗微小卫星接管控制失效卫星的姿态运动提供了新思路。文献[12-13]针对失效卫星的姿态接管控制问题,设计了微小卫星的非零和微分博弈控制器。所设计的控制器能够在避免进行微小卫星控制分配的情况下,通过各颗微小卫星独立优化各自局部性能指标函数的方式获得控制策略。由于非零和博弈为非合作博弈,因此文献[12-13]实现的是对各颗微小卫星局部性能指标函数的优化。为实现对所有微小卫星全局性能指标函数的优化,文献[14]设计了微小卫星的合作博弈控制器,与文献[12-13]中的研究相比,提高了微小卫星性能指标函数的优化程度。但由于仅获得了微小卫星合作博弈的开环控制策略,难以实现对控制误差的补偿。
本文在文献[12-14]研究的基础上,考虑并设计能够满足微小卫星控制约束的闭环合作博弈控制方法。所设计的方法通过过去与当前时刻数据的并行使用,放松了微小卫星合作博弈策略学习对持续激励条件的要求,避免了系统抖振的发生。所获得的合作博弈方法可有效满足微小卫星控制约束,且能够在避免进行控制分配的情况下获得各微小卫星的控制策略,计算复杂度低。
1 问题描述
利用微小卫星进行失效卫星的姿态接管控制需要多颗微小卫星通过互相协同提供失效卫星姿态运动所需的控制力矩。图1给出了失效卫星姿态接管控制示意图。
假设:
(1) 各微小卫星固连于失效卫星,且相对于失效卫星的方位保持不变。
(2) 失效卫星与微小卫星所形成的组合体可视为刚体。
(3) 失效卫星姿态运动所需的控制力矩完全由微小卫星提供。
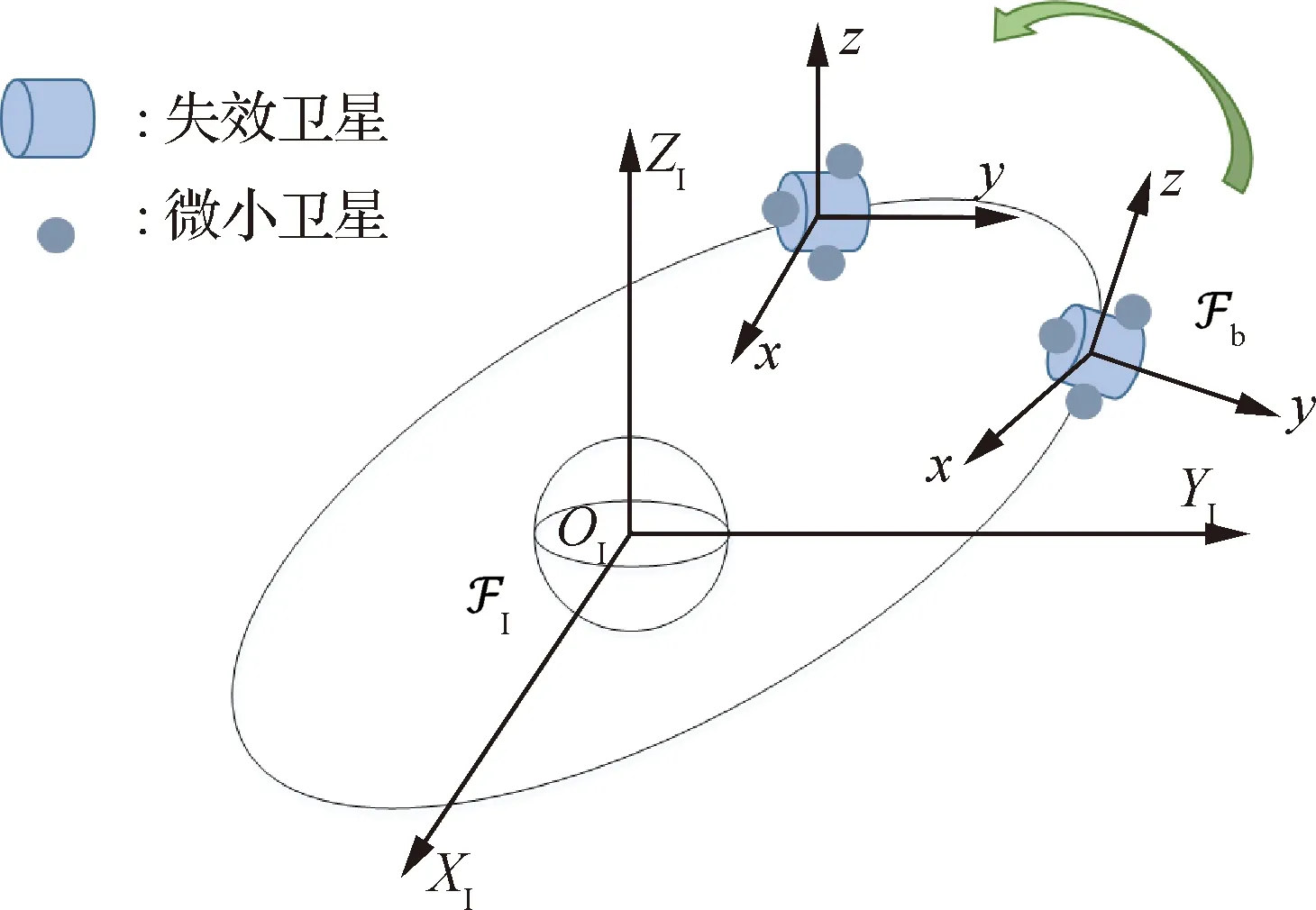
图1 失效卫星姿态接管示意图Fig.1 Shetch of attitude takeover of failed satellite
本文在考虑微小卫星控制约束的情况下,设计多星闭环合作博弈控制器。首先,通过组合体动力学模型的建立及考虑微小卫星控制约束的性能指标函数的设计,建立微小卫星合作博弈模型;其次,面向协同优化微小卫星全局性能指标函数的需求,设计微小卫星合作博弈帕累托最优策略学习方法,以进行微小卫星闭环合作博弈策略的学习;最后,根据学习到的合作博弈策略进行微小卫星的闭环协同控制,并基于此实现对失效卫星姿态运动的接管控制。
本文所使用的坐标系定义如下:

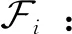
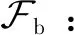
2 微小卫星合作博弈模型
文献[12]为实现微小卫星控制策略的独立计算,将失效卫星姿态接管控制问题建模为非合作博弈问题,所实现的是各颗微小卫星局部性能指标函数的优化,且未考虑微小卫星的控制约束。为实现对所有微小卫星全局性能指标函数的优化,本节首先在考虑微小卫星控制约束的情况下,将失效卫星姿态接管控制问题建模为微小卫星的合作博弈问题。
2.1 组合体姿态运动模型
本文通过修正罗德里格斯参数(Modified Rodrigues Parameter, MRP)进行组合体姿态运动的描述,相应的组合体姿态运动学方程为

(1)
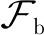
(2)
其中:I为单位阵;σ×为σ=[σ1,σ2,σ3]T的反对称矩阵,σ×=[0,-σ3,σ2;σ3,0,-σ1;-σ2,σ1,0]T。
组合体姿态动力学方程为
(3)
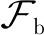
定义组合体状态变量为x=[σT,ωT]T,根据式(1)与式(3),可得组合体姿态运动方程为
(4)
式中:
(5)
2.2 微小卫星合作博弈建模
为通过多颗微小卫星的互相协同实现对失效卫星姿态运动的接管控制,为微小卫星设计如下的性能指标函数:

(6)
式中:ri(x,ui)=xTQix+φi(ui);Qi为一对称正定矩阵;x0为组合体状态变量初值;t0为接管控制初始时刻。
为了处理微小卫星的控制约束,φi(ui)定义为[16]
(7)
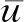
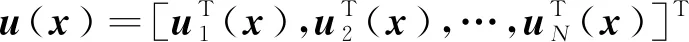
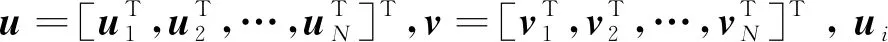
(8)
当微小卫星的合作博弈策略达到帕累托最优时,任意的策略改变至少会使一颗微小卫星性能指标函数的最优性受到损失。因此,通过使用微小卫星合作博弈的帕累托最优策略,能够在优化微小卫星全局性能指标函数的情况下,实现对失效卫星的姿态接管控制。
帕累托最优策略可通过优化各颗微小卫星局部性能指标函数的加权组合来获得,即
(9)
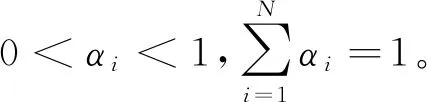
在考虑组合体动力学约束、微小卫星控制约束的情况下,微小卫星合作博弈可描述为
(10)
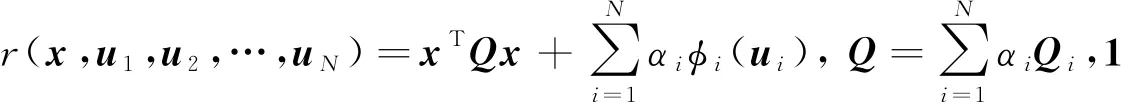
3 微小卫星合作博弈策略显式表达式
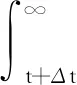
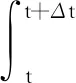
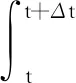
(11)
将V(x(t+Δt))通过泰勒级数展开,可得
(12)
由于在控制策略u作用下,式(4)中标称系统为一定常系统,因此∂V/∂t=0。将式(12)代入式(11)中,并以Δt除之,当Δt→0时,可得
(13)
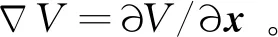
定义哈密尔顿函数为
(14)
令∂H/∂ui=0,可得微小卫星i最优控制显式表达式为
(15)
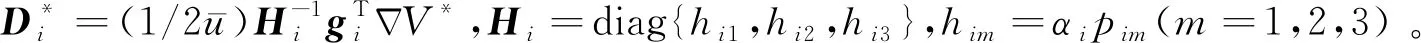
注1由于tanh函数的值域为(-1,1),因此,当微小卫星采取式(15)中的控制策略时,微小卫星控制约束将能够得到满足。
(16)
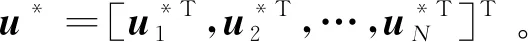
将式(16)代入式(13)中,可得HJB方程为
(17)
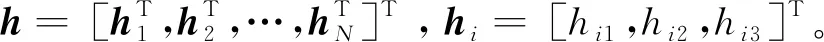
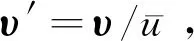
(18)
将式(18)代入式(17)中,HJB方程可改写为
(19)
4 微小卫星并行学习合作博弈控制方法
本节通过过去与当前时刻数据的并行使用,设计能够进行微小卫星合作博弈策略学习的策略迭代方法,并在此基础上进行微小卫星合作博弈帕累托最优策略数值解的学习。
4.1 神经网络权值矢量更新律设计
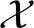
V*(x)=WTφ(x)+εV(x)
(20)
式中:W为神经网络理想权值矢量;φ(x)=[φ1(x),φ2(x),…,φK(x)]为激活函数矢量;K为隐藏层神经元数量;εV(x)为逼近误差。
最优值函数关于x的微分为
(21)
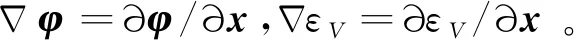
微小卫星合作博弈策略为
(22)
式中:εu*为合作博弈策略逼近误差。
将式(21)代入HJB方程(19)中,可得
(23)
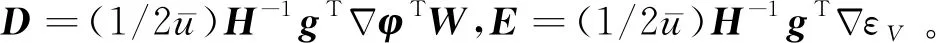
定义HJB方程逼近误差为
(24)
式(23)可改写为
(25)
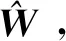
(26)
最优值函数关于x的微分的逼近值为
(27)
微小卫星合作博弈策略逼近值为
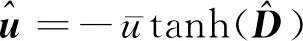
(28)
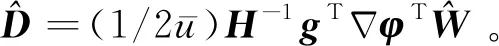
将式(27)代入式(19)中,可得
(29)
式中:
(30)
定义:
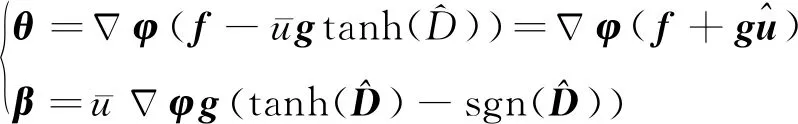
(31)
式(30)可改写为[19]
(32)
式中:
(33)
为了进行式(19)数值解的学习,文献[19]通过优化如下仅依赖于当前时刻系统状态的误差范数进行神经网络权值矢量的学习:
(34)
然而,通过优化误差范数(34)进行神经网络权值矢量的学习要求信号θ满足如下持续激励条件:
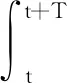
(35)
式中:t为当前时刻;T为神经网络权值矢量学习过程中的动力学积分步长;κ1与κ2均为正数。
持续激励条件一般通过引入噪声来得到满足[12,19],然而,这会造成系统状态持续不断的抖振,从而对系统的稳定性甚至安全性产生不利影响。文献[20]中的研究表明,通过对当前与过去时刻数据的并行使用,可放松参数辨识方法对持续激励条件的要求。本文通过并行学习思想进行无需持续激励条件的神经网络权值矢量更新律的设计。为此,考虑如下的误差范数:
(36)
式中:ek为e在过去时刻系统状态变量xk处的取值;p为使用的过去时刻系统状态变量的数量。
无需持续激励条件的神经网络权值矢量更新律可设计为
(37)
式中:θk与βk分别为θ与β在过去时刻系统状态变量xk处的取值。

证明:定义如下的Lyapunov函数:
(38)
其导数为
(39)
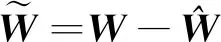
(40)
记:
(41)
则有:
(42)
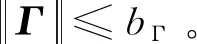
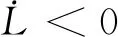
(43)

4.2 基于并行学习的策略迭代方法
微小卫星合作博弈策略可通过基于并行学习的策略迭代方法进行计算。具体执行步骤如下:
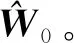
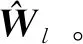
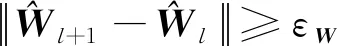
(44)

注3式(44)中的合作博弈策略具有反馈控制形式,当扰动存在并造成失效卫星的姿态接管控制误差时,反馈控制策略(44)能够通过对微小卫星合作博弈策略的调整进行误差的实时补偿,以实现对失效卫星姿态运动的闭环控制。
5 仿真校验
本节通过数值仿真对所设计的微小卫星合作博弈控制方法的有效性,及其与现有研究相比在放松持续激励条件、处理微小卫星控制约束及抑制扰动方面的优势进行验证。
不失一般性,假设有4颗微小卫星参与进行失效卫星的姿态接管控制。失效卫星与微小卫星所形成的组合体的转动惯量为
4颗微小卫星本体坐标系到组合体本体坐标系的转换矩阵分别为
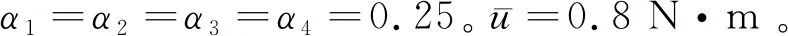
仿真分2个阶段,第1个阶段通过并行学习策略迭代方法进行神经网络权值矢量的学习,以获得微小卫星的合作博弈策略。第2个阶段根据获得的合作博弈策略进行微小卫星的闭环协同控制,以实现对失效卫星姿态运动的接管控制。
5.1 神经网络权值矢量学习
仿真中使用50个过去时刻数据与当前时刻数据进行神经网络权值矢量的并行学习。组合体初始姿态MRPσ0=[1.307 6,1.216 4,0.465 9]T,初始姿态角速度ω0=[0.002 2,0.012 0,0.059 5]Trad·s-1。


图2 组合体姿态MRP随时间变化曲线(神经网络权值矢量学习阶段)Fig.2 Variation of attitude MRP of combination (NN weights learning stage)
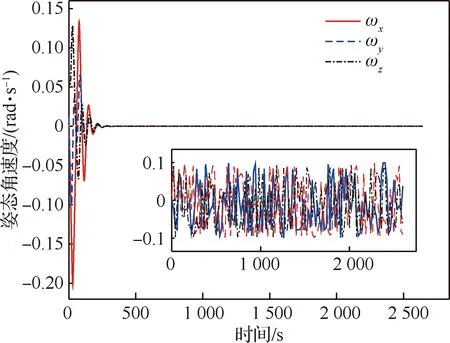
图3 组合体姿态角速度随时间变化曲线(神经网络权值矢量学习阶段)Fig.3 Variation of attitude angular velocity of combination (NN weights learning stage)
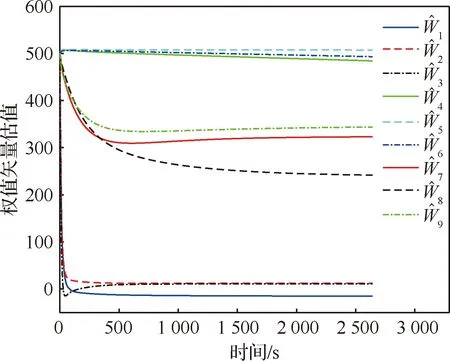
图4 神经网络(NN)权值矢量估值随时间变化曲线Fig.4 Variation of NN weight estimations
5.2 失效卫星姿态接管控制
获得神经网络权值矢量估值之后,便可根据式(44)直接计算各颗微小卫星的合作博弈策略,以进行失效卫星的姿态接管控制。假设在姿态接管控制阶段,组合体初始姿态MRP及角速度分别为σ0=[-0.455 3,0.355 0,0.122 5]T及ω0=[0.015 0,0.006 0,-0.008 6]Trad·s-1。期望姿态MRP及角速度分别为σf=[0,0,0]T及ωf=[0,0,0]Trad·s-1。
图5与图6分别给出了组合体姿态MRP及角速度随时间变化的曲线,可以看出,在多颗微小卫星的合作博弈控制下,组合体的姿态MRP与角速度均得到了有效控制。
图7给出了4颗微小卫星控制力矩随时间变化的曲线,其中蓝绿色实线为文献[12]方法所得的微小卫星控制力矩曲线,绿色虚线表示微小卫星的控制约束。可以看出,与文献[12]方法相比,本文方法能够在整个姿态接管控制过程中,使微小卫星的控制约束得到满足。
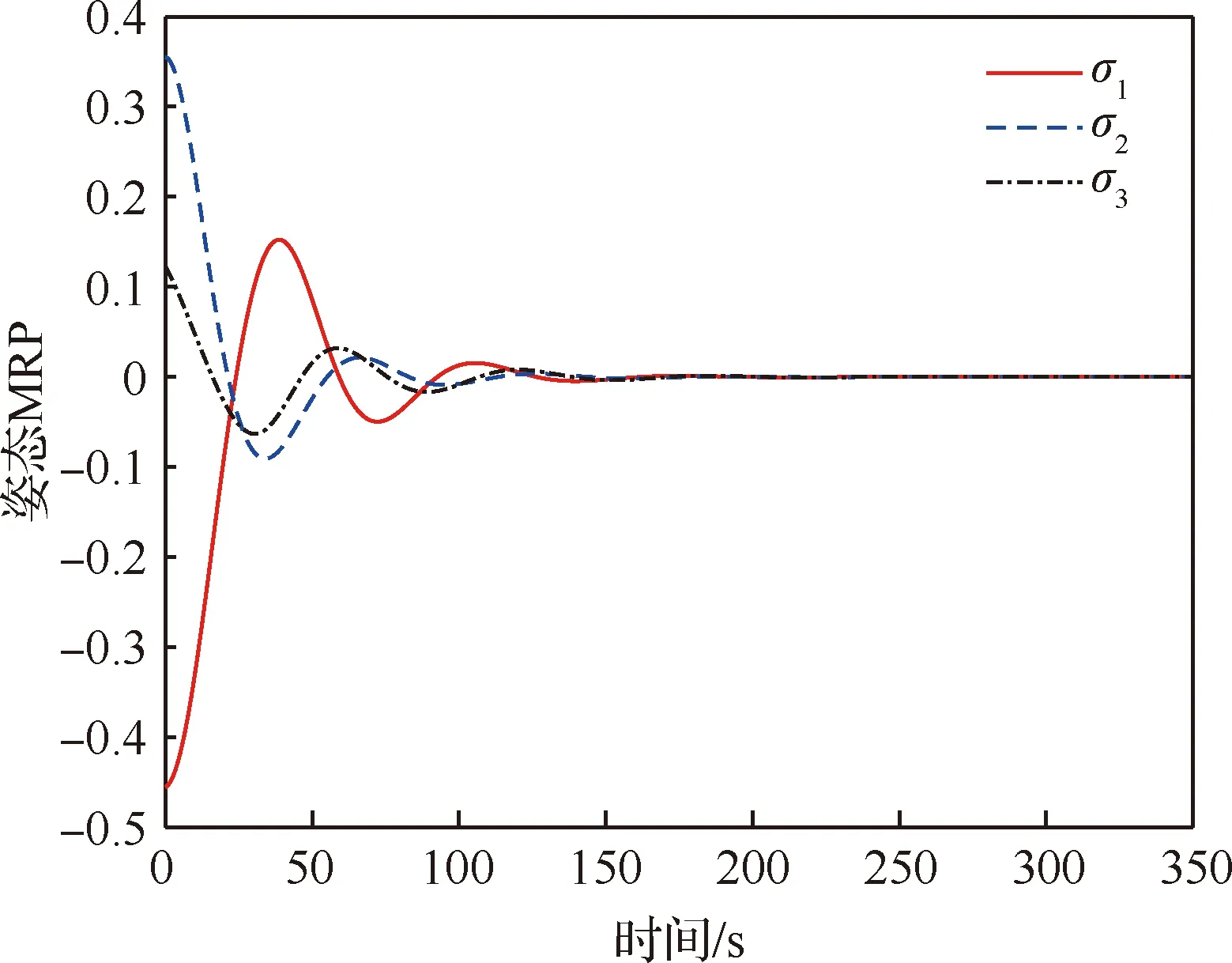
图5 组合体姿态MRP随时间变化曲线(姿态接管控制阶段)Fig.5 Variation of attitude MRP of combination (attitude takeover control stage)
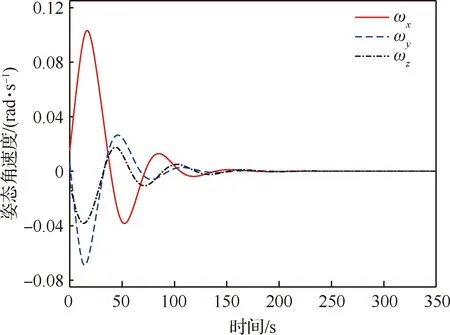
图6 组合体姿态角速度随时间变化曲线(姿态接管控制阶段)Fig.6 Variation of attitude angular velocity of combination (attitude takeover control stage)
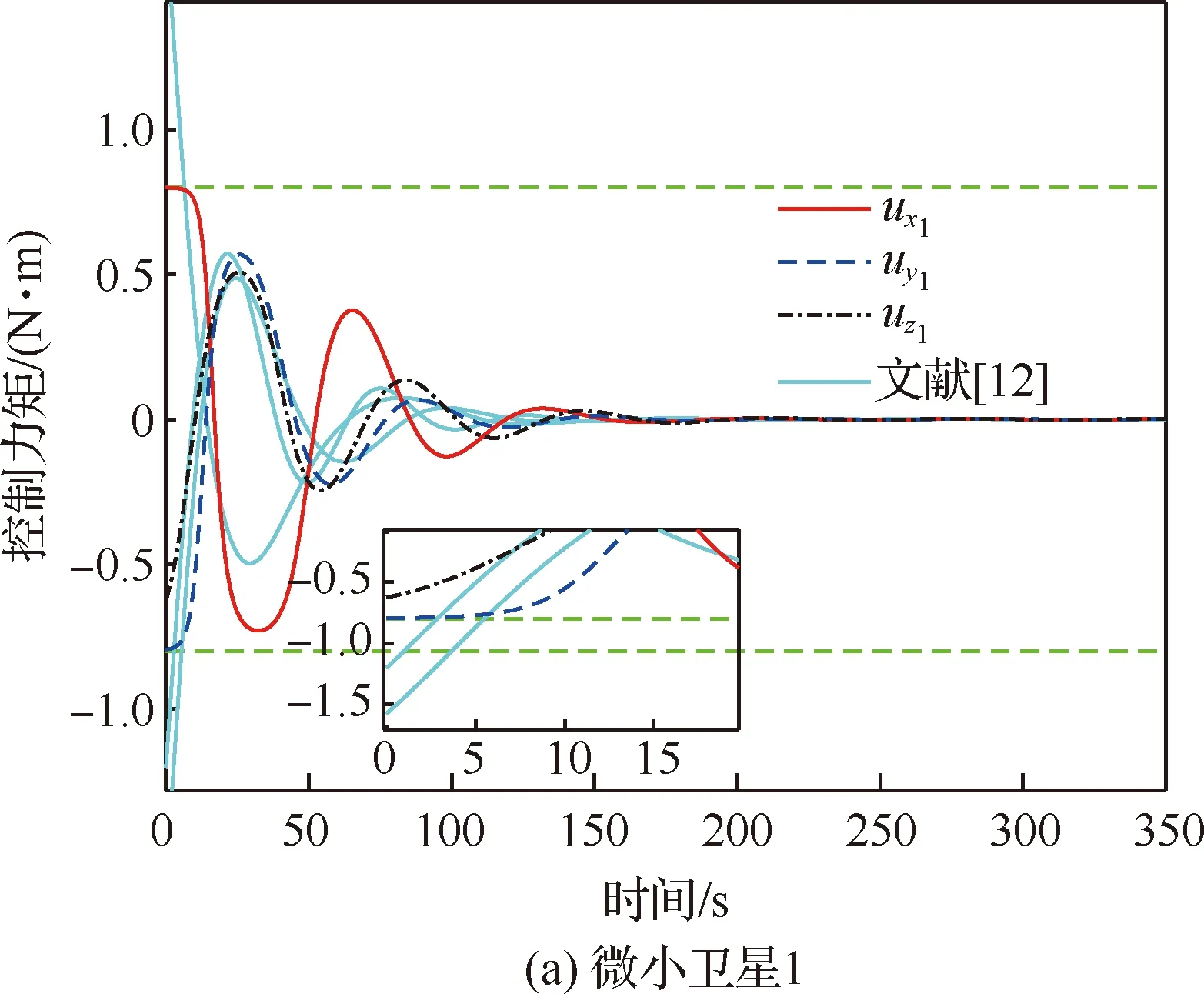
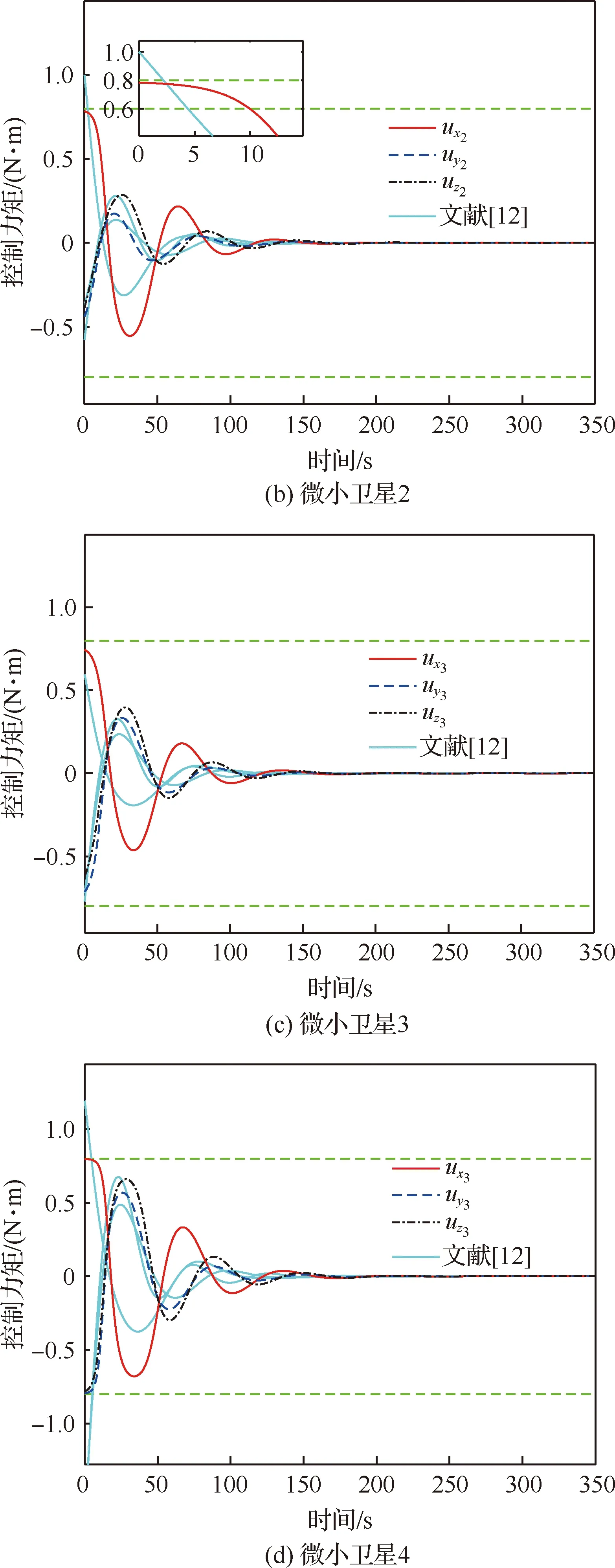
图7 微小卫星控制力矩随时间变化曲线(姿态接管控制阶段)Fig.7 Variation of control torque of microsatellites (attitude takeover control stage)
5.3 扰动存在情况下的失效卫星姿态接管控制
为验证所获得的闭环合作博弈策略对扰动引起的姿态控制误差的补偿能力,在姿态接管控制过程中引入如下的干扰力矩:

组合体初始姿态MRP 及角速度分别为σ0=[-0.355 3,-0.205 0,0.082 5]T,ω0=[-0.015 3,0.040 0,-0.048 6]Trad·s-1。期望姿态MRP及角速度为σf=[0,0,0]T,ωf=[0,0,0]Trad·s-1。
图8与图9分别给出了组合体姿态MRP及角速度随时间变化的曲线,其中蓝绿色实线为文献[14]方法所得的姿态MRP及角速度曲线。由于文献[14]主要关注微小卫星开环合作博弈策略的确定,因而难以实现对扰动所造成的失效卫星姿态控制误差的补偿。本文方法得到了微小卫星的闭环合作博弈策略,能够在扰动存在的情况下,实现对组合体姿态MRP与角速度的有效控制。
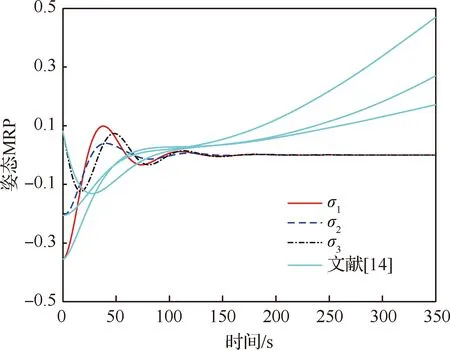
图8 组合体姿态MRP随时间变化曲线Fig.8 Variation of attitude MRP of combination
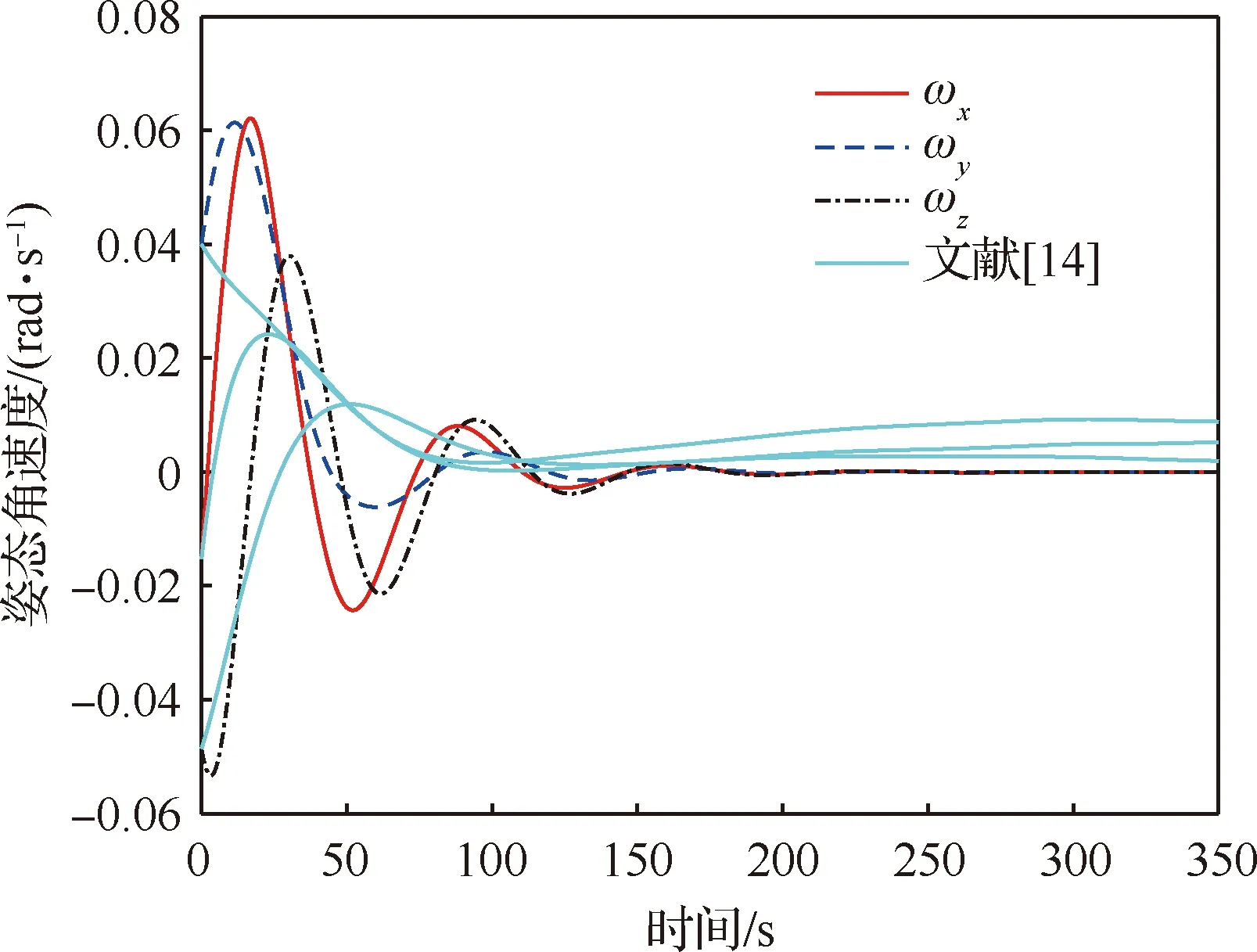
图9 组合体姿态角速度随时间变化Fig.9 Variation of attitude angular velocity of combination
6 结 论
1) 针对多颗微小卫星接管控制失效卫星姿态运动的问题,提出了一种能够处理微小卫星控制约束的并行学习合作博弈控制方法。该方法通过过去与当前时刻数据的并行使用,放松了微小卫星合作博弈策略的学习对持续激励条件的要求,有效避免了博弈策略学习过程中系统抖振的发生。
2) 所获得的微小卫星合作博弈策略具有反馈控制形式,一旦完成博弈策略的学习,各颗微小卫星便能通过控制策略的独立计算实现对失效卫星姿态运动的闭环控制,以实现对控制误差的补偿。
