基于CS-SNN的公交到站时间预测模型*
2021-03-26邝先验罗会超欧阳鹏
邝先验, 罗会超, 钟 蕊, 欧阳鹏
(江西理工大学 电气工程与自动化学院,江西 赣州 341000)
0 引 言
在许多大型城市,人们常常把城市福利和公交出行联系在一起。私有汽车数量、城市人口的增加和许多不确定因素导致传统的公交到站时间预测方法准确率较低,进而影响乘车人的出行。考虑到传统预测的不足在很大程度上影响大众出行选择和公交公司的收益。因此,寻找更加有效的公交到站时间预测方法显得日益重要。
目前,国内外学者对公交到站时间预测进行多种研究,如文献[1]提出将公交到站时间表现形式分为不同路段的运行时间和不同站点的停靠时间,以及上班日和休息日的公交到站数据;文献[2]针对公交全球定位系统(GPS)数据进行公交到站时间预测,提出了一种新型模糊隶属度算法;胡继华等人[3]划分不同时段下的公交GPS数据,并利用移动误差补偿改进了马尔科夫链预测模型;Peng Z等人[4]针对支持向量机应用时输入指标之间的相关性和核函数参数标定的不足,提出了一种基于主成分分析(principal component analysis,PCA)—遗传算法(genetic algorithm,GA)—支持向量机(support vector machine,SVM)的预测方法,以提高公交车到达时间预测的精度;文献[5]根据客流分配关系、上下车人数、车内拥挤度、建立旅客上下车时间预测模型,再通过对比时间关系进行回归分析。
上述研究方法虽然在某种程度上取得了一定效果,但依旧比较传统,主要是第一代或第二代神经网络模型,部分神经网络自身具有局限性和适用性,因此,许多模型在更换数据种类后,仍然无法更加精准地预测结果。本文在考虑时空特性的基础上,采用第三代神经网络中最接近生物神经元的Spiking神经网络(spiking neural network,SNN),考虑了时间信息的影响。同时,利用搜索能力更强的布谷鸟搜索(cuckoo search,CS)算法优化SNN模型初始参数,进一步提高了全局搜索能力、预测的准确性和稳定性。在公交到站时间预测的实际应用中,预测效果相比传统神经网络更好。
1 SNN脉冲神经网络
最近几年,随着人工时间网络的发展,许多学者聚焦在第三代神经网络模型,例如:Spike神经元模型的神经网络[6]。与传统的神经元传递函数不同,Spiking神经元是SNN的基本单元,Spike模型根据神经元传递时间点对信息进行编码,使得该模型更近似于生物神经元。在SNN中,学习算法的选取对其性能有着至关重要的影响,除了无监督学习算法外,文献[7]中提出的SpikeProp(spike propagation,Prop)算法具有有效的监督学习能力,本文选用其脉冲响应模型(spike response mode,SRM) 中一种0阶简化模型SRM0当作脉冲响应模型[8], SRM0模型采用3层前向SNN结构,以神经元h和i连接为例,进一步分析任意相邻两个神经元间的连接结构,如图1所示。
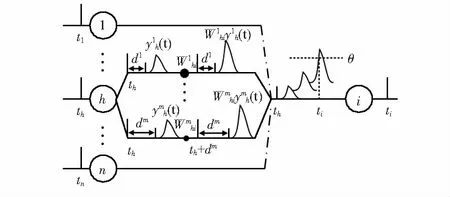
图1 神经元间多个有延迟突触终端的连接
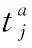
(1)
(2)
(3)
(4)
虽然脉冲神经网络特有的编码方式和多突触结构,使其拥有良好的运算能力和极佳的适用能力。但是,该算法仍然使用梯度信息进行参数的重置,同样易于陷入局部最优解。此外,网络中相邻神经元之间为多突触连接,连接权值的选取存在一定的制约。因此,本文利用CS算法对SNN进行有监督学习,克服了该算法的不足。对公交到站时间的预测结果表明:CS算法能很好地弥补SNN的缺陷。
2 CS算法优化SNN预测模型
2.1 CS优化算法
通过模拟布谷鸟巢寄生育雏行为,剑桥大学杨新社和戴布 S教授提出了一种新兴启发算法:CS算法[9,10]。CS算法的关键参数仅为外来鸟蛋被发现的概率和种群数目,整个算法操作简单、易于实现。作为一种通用型算法,CS 算法易于与其他算法相结合,进而获得性能更加优越的混合算法[11]。
布谷鸟寻找宿主鸟巢的位置更新公式如下
(5)
(6)
根据上述过程,CS算法优化SNN预测公交到站时间的实现过程如下:
Step1 首先收集公交行车历史数据,结合有代表性的数据特点,确定神经网络的输入、隐含层和输出层结构。
Step2 设置CS算法最小和最大步长、迭代次数200次、初始的概率参数Pa=0.5,在给定的空间范围内随机产生n个鸟巢P0=(p1(0),p2(0),…,pn(0))。其中每个鸟巢代表一组将要优化训练的SNN的连接权值与突触连接的延时参数,按照适应度函数进行计算(适应度函数为均方差误差函数),找到当前最优的鸟巢位置pb(0)。
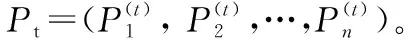
Step4 将迭代多次的最优质的鸟巢pb(t+1)作为SNN的网络连接权值与突触连接的延时参数,再训练神经网络,最终输出公交到站时间的预测结果并分析。
2.2 隐含层神经元数确定
本文采用单个隐含层的网络结构,并根据经验公式计算隐含层节点数
(7)
式中L为隐含层神经元数,x为输入神经元数,y为输出神经元数,同时q取整数大于1且小于10。为了选择最适合的L值,下文对不同神经元数的网络模型进行预测误差分析。
2.3 预测模型性能评估指标
对公交站到站时间的预测误差分析,本文使用平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE)误差分析法
(8)
(9)
(10)
式中Yi为真实数据,Pi为预测数据,n为预测数据个数。
3 实例仿真与结果分析
3.1 样本数据的预处理及预测
以2017年中国赣州公交总站历史记录数据中K1公交车的数据作为研究对象,选择3月1日到3月15日中周一至周日的全部公交到站时间点作为预测数据,此外,分别选择3月23日(周四)和3月25日(周六)的到站时间点作为测试数据。为了进一步提高精度,先将到站时间点转换为时间戳,即指格林威治时间自1970年1月1日(00∶00∶00 GMT)至当前时间的总秒数,再分别利用Elman,SNN和CS-SNN预测模型进行仿真实验,通过误差对比,分析三种模型的预测性能。软件程序在MATLAB 2018a上运行,操作系统是Windows10旗舰版64位。预测流程如图2所示。
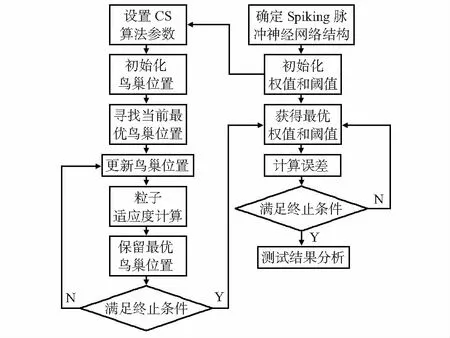
图2 预测流程图
3.2 预测模型及方法
本文采用神经网络对数据进行预测和分析,选择3月23日(周四)和3月25日(周六)的到站时间点作为测试数据,利用前三站的到站时刻去预测下一站到站时刻,下一次预测时,用第四个时刻真实值代替的预测值进行循环预测。
SNN 的输入、输出数据编码采用Time-to-first-spike方法[12]。两个相连神经元之间突触子个数m和隐含层神经元个数均影响着SNN性能。故在测试过程中先对突触子个数和隐含层神经元个数进行了探讨。根据经验公式选择最佳的隐含层神经元个数,计算不同隐含层神经元个数下的平均绝对误差,取多次实验的平均值,验证得到最佳参数设置:算法为Spike Prop,编码方式为Time-to-first-spike,传递函数为脉冲响应,输入层神经元个数为3,隐含层神经元个数为8,输出层神经元个数为1,突触子连接数为16,PSP衰减时间常数τ为6 ms,激发阈值θ为1 mV,算法的迭代步长为0.1 ms,网络学习率η为0.05。
3.3 预测结果及分析
为了增加实验结果的稳定性,分别对每种预测模型进行10次实验,预测结果取10次实验的平均值。将训练数据的均方误差作为子种群的适应度函数,对比CS算法和粒子群算法适应度曲线变化,如图3所示。
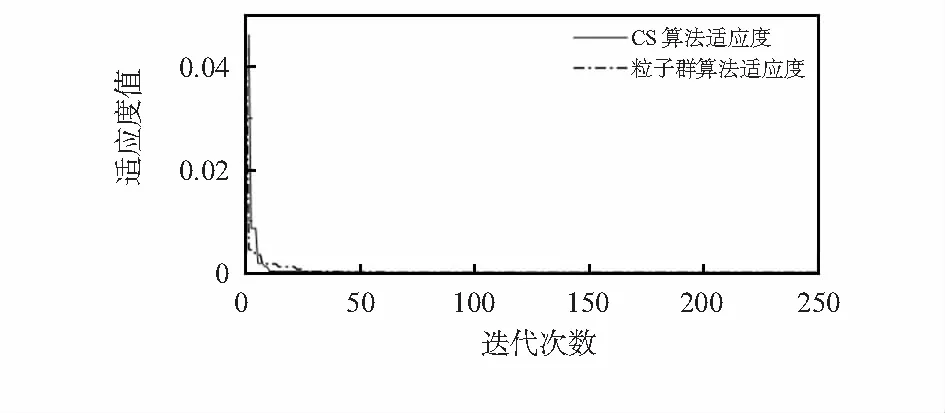
图3 CS和粒子群算法优化适应度对比
由图3可知,在到站时刻预测中CS优化算法的适应度下降速度明显大于粒子群算法,且下降过程波动性更小。
取工作日公交行驶数据分别代入网络进行预测,用实际值减去预测值,进一步分析误差如图4和表1所示。
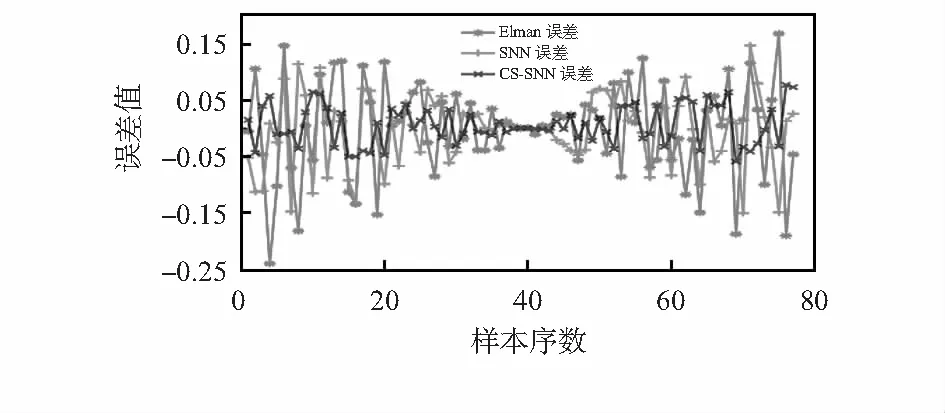
图4 工作日到站预测误差
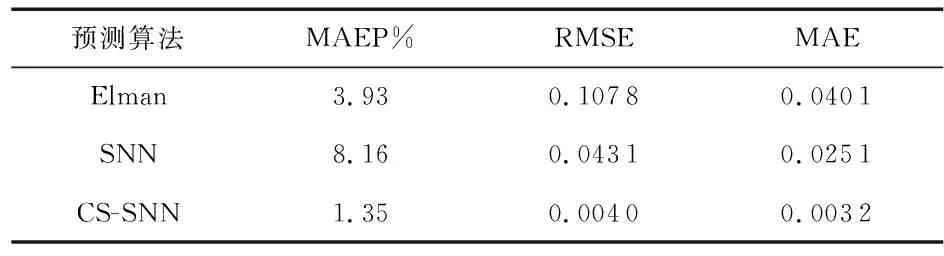
表1 不同优化算法预测误差
由图4和表1可知,CS-SNN模型预测误差最小,预测值更加准确。
同理,取周末公交行驶数据分别代入网络进行预测,用实际值减去预测值,进一步分析误差如图5和表2所示。
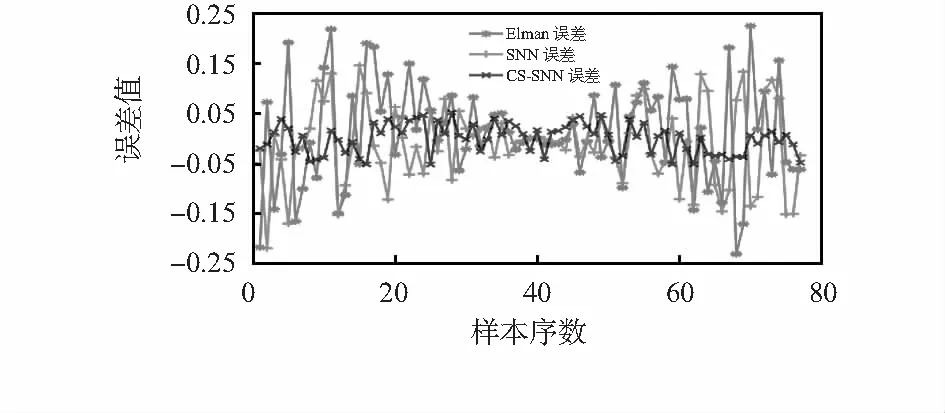
图5 周末到站预测误差
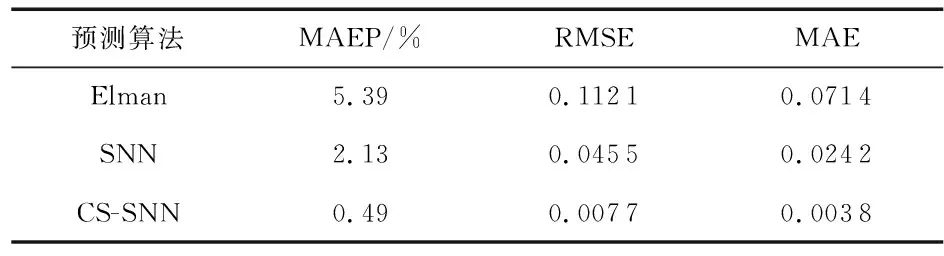
表2 不同优化算法预测误差
由图5和表2可知,同样是CS-SNN模型预测误差最小,预测值更加准确。
本文利用公交历史实测数据对未来短期公交到站时间进行预测,并分析工作日和周末两个时间段预测模型的性能。结果表明CS-SNN模型,相比于传统网络模型,对公交到站时间预测有良好的效果,无论是工作日还是周末均可做到精准的预测,其精度明显高于未优化的SNN,是一种更加有效的公交到站时间预测方法。
4 结 论
1)利用赣州市K1公交车历史记录数据对Elman,SNN,CS-SNN三种预测模型性能进行对比分析。通过测试结果可以看出:SNN比传统的预测模型精确度更高。
2)布谷鸟优化算法弥补了SNN预测中易陷入局部最优等缺陷,使得模型对非线性数据处理能力更强、稳定性更好、适用性较高,预测效果得到进一步提升。
3)从输入数据的角度分析,公交到站预测模型仍然具有研究空间。目前的研究主要集中在运行时间和运行路线两种因素,此外如何有效结合道路情况、天气气候等因素,也将是提高到站时间预测精度的方向。
