利用动量定理求解位移相关问题

2021-03-26薛彦学

物理教师 2021年2期

关键词：动量定理铅球电场

薛彦学

(莒县第一中学，山东莒县 276500)

1 动量定理与斜抛运动的水平位移

图1

例1.(第35届全国中学生物理竞赛预赛第6题的试题)如图1所示,田径场上某同学将一铅球以初速度v0抛出,该铅球抛出点的最大高度为h,

铅球在田径场上的

落点与铅球抛出点的最大水平距离为________,对应的抛射角为________．

解析:这道题一般都用正交分解法,分别列出水平和竖直方向的运动学方程,然后整理成关于水平位移L和抛射角θ的函数,利用函数求出极值,无疑运算量是十分巨大的,[1]没有十几分钟不可能解出来,作为一个填空题,显然是不合理的．有没有相对简单的思路呢?我们可以考虑利用机械能守恒和动量定理,问题转化为一个三角形面积求极值．具体解法如下.

设铅球质量为m,抛出后经t秒落地,落地速度大小为v,水平位移为l,由机械能守恒定律，可得

(1)

(2)

水平位移

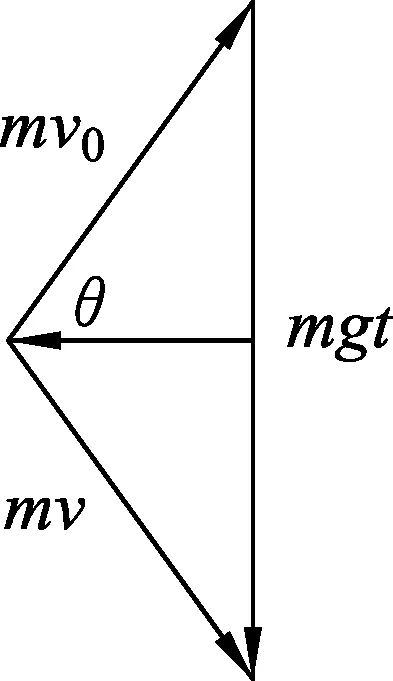
图2

l=(v0cosθ)t.

(3)

由动量定理

mgt=mv-mv0.

(4)

3者组成矢量三角形如图2所示，消去m,则三角形的面积

(5)

整理得

(6)

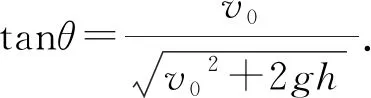
显然,利用动量定理的矢量形式,计算过程要简洁的多．

点评:本题利用动量定理的矢量形式中,三角型的面积与斜抛运动水平位移对应,从而巧妙解决．

2 动量定理与圆周运动的水平位移

2.1 特殊结论的理论证明

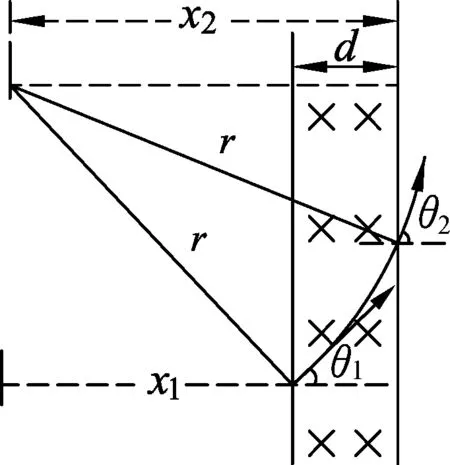
图3

证明1:如图3所示带电粒子在匀强磁场中运动轨迹半径为r，

(1)

由几何关系

(2)

由(1)、(2)式得

证明2:带电粒子在磁场运动过程任取极短时间Δt,用竖直方向由动量定理[2]

qvxBΔt=mΔvy，

(3)

其中洛伦兹力的竖直分量与水平速度分量对应，vxΔt=Δx对应这段时间的水平位移,可得

qBΔx=mΔvy.

(4)

对整个在匀强磁场中运动过程求和得

qB∑Δx=m∑Δvy.

(5)

qBd=m(vy2-vy1).

(6)

变形可得

上述证明过程表明洛伦兹力作用下物体做匀速圆周运动,也可以在某个方向用动量定理.

2.2 典型问题

例2.(2015年天津高考第12题)现代科学仪器常利用电场、磁场控制带电粒子的运动．真空中存在着如图4所示的多层紧密相邻的匀强电场和匀强磁场,电场与磁场的宽度均为d．电场强度为E．方向水平向右;磁感应强度为B.方向垂直纸面向里．电场、磁场的边界互相平行且与电场方向垂直．一个质量为m、电荷量为q的带正电粒子在第1层电场左侧边界某处由静止释放.粒子始终在电场、磁场中运动,不计粒子重力及运动时的电磁辐射．

(1) 求粒子在第2层磁场中运动时速度v2的大小与轨迹半径r2.

(2) 粒子从第n层磁场右侧边界穿出时,速度的方向与水平方向的夹角为θn.试求sinθn.

(3) 若粒子恰好不能从第n层磁场右侧边界穿出.试问在其他条件不变的情况下,也进入第n层磁场.但比荷较该粒子大的粒子能否穿出该层磁场右侧边界,请简要推理说明之．

图4

解析:这道题第1问比较简单,第2、3问常规思路解答相当繁琐,我们用刚才推论重点分析第2、第3问．

粒子从静止出发到从第n层磁场右侧边界穿出过程中只有电场力做功，

(1)

竖直方向运用运动动量定理的特殊推论并求和的得

(2)

其中nd为带电粒子在n层磁场中运动的水平位移之和,电场力水平不改变竖直方向动量,由几何关系

(3)

由(1)和(2)式得

(4)

有了第2问的结果,第3问就迎刃而解.如果粒子恰不能从右边界射出,则sinθn=1,由(4)式,比荷大的粒子经过n层电磁场后,速度偏向角的正弦值就会大于1,故不可能．

图5

例3.(2011年山东高考题)扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆．其简化模型如图5Ⅰ、Ⅱ两处的条形匀强磁场区边界竖直,相距为L,磁场方向相反且垂直于纸面．一质量为m、电荷量为-q、重力不计的粒子,从靠近平行板电容器MN板处由静止释放,极板间电压为U,粒子经电场加速后平行于纸面射入Ⅰ区,射入时速度与水平方向夹角θ=30°.

(1) 当Ⅰ区宽度L1=L、磁感应强度大小B1=B0时,粒子从Ⅰ区右边界射出时速度与水平方向夹角也为30°,求B0及粒子在Ⅰ区运动的时间t0.

(2) 若Ⅱ区宽度L2=L1=L磁感应强度大小B2=B1=B0,求粒子在Ⅰ区的最高点与Ⅱ区的最低点之间的高度差h.

(3) 若L2=L1=L、B1=B0,为使粒子能返回Ⅰ区,求B2应满足的条件.

(4) 若B1≠B2,L1≠L2,且已保证了粒子能从Ⅱ区右边界射出．为使粒子从Ⅱ区右边界射出的方向与从Ⅰ区左边界射入的方向总相同,求B1、B2、L1、、L2、之间应满足的关系式．

解析:本题前3问比较基础,我们重点分析第4问．

方法1.常规思路，由向心力公式可得

(1)

(2)

如图6(或图7)所示,设粒子射出磁场Ⅰ区时速度与水平方向的夹角为α.