基于自旋回波探测的地面磁共振T2 谱正反演策略*
2021-03-26杨玉晶叶瑞赵汗青万玲2林婷婷2
杨玉晶 叶瑞 赵汗青 万玲2) 林婷婷2)†
1) (吉林大学仪器科学与电气工程学院, 长春 130061)
2) (地球信息探测仪器教育部重点实验室(吉林大学), 长春 130061)
1 引 言
过去人们探测地下水主要采用的是电法和电磁法[1-4], 通过探测含水构造或者含水结构体, 从而评价地下水的赋存状态, 然而这些方法都是间接方法, 无法直接对地下水进行定性、定量估计, 也难以直接获得赋水层相关参数.相比于传统电磁法,地面磁共振(magnetic resonance sounding, MRS)技术以其无损、原位, 且独有的直接探测优势, 被广泛应用于浅层地下水勘探、水源性地质灾害预测等领域[5].通常, 在实施探测时, 仅需施加地磁场( B0)条件下的拉莫尔频率( f0)交流场, 激发自由水中氢原子核进动, 即可探知饱和地下水存在、含量及其赋存状态.激发结束后, 收集氢原子核能释产生的自由感应衰减(free induction decay, FID)信号, 其初始振幅、平均弛豫时间分别与地下含水量w、饱和水孔隙分布相关[6-8].近年来, 地面MRS 相关理论与方法日趋成熟, 其正反演技术已经由简单的一维层状水探测成像逐渐发展为更为复杂的二维、三维成像[9-13].然而, 受单脉冲激发序列限制, 现有技术仍局限在w 及探测及解释,在某些特定探测环境下, FID 信号易受地下铁磁性介质影响而大幅缩短(衰减快), 造成含水结构赋存状态估测误差极大[14-16].
相比于传统的FID 探测, 基于自旋回波(spin echo, SE)信号的横向弛豫时间 T2探测适应性更强, 不仅能够更为准确地估计地下水孔隙分布、渗透率[17-20], 且在水力传导率等更多水文地质信息预测方面表现出一定潜力[21,22], 是目前地面MRS 领域的国际热点问题.与测井技术中应用的自旋回波探测序列[23]相似, 地面磁共振 T2探测通常由多组双脉冲或多脉冲CPMG (Carr-Purcell-Meiboom-Gill)序列[24,25]激发, 通过拟合自旋回波峰值并代入反演, 得到地下水w 和 T2分布.随着相关探测需求的提出, 兼具双脉冲及CPMG 序列发射功能的地面MRS 仪器应运而生[26].但由于早期工作更多出于检测短弛豫信号的基本需要, 相关数据建模及解释方法并无明显发展, 仍采用与普通FID 信号相似策略, 即将SE 信号包络峰值拟合线作为原始信号, 直接代入反演求解, 获取地层含水信息[17].
为了更好地预测地下水赋存状态, 充分利用SE 信号携带信息, 2014 年, Grunewald 等[19]提出了基于线性空间变换-非线性拟合的 T2反演框架.即首先通过奇异值分解(singular value decomposition, SVD)法[27]将时域自旋回波信号与脉冲矩间的函数关系变换至与层深相关, 得到地下水SE 分布; 随后通过非线性拟合地下水SE 结果, 求得w 和 T2信息.该方法的提出, 直接建立了w 和T2与深度间的空间关系, 有效避免了原信号峰值取样-反演拟合流程产生的二次误差.然而, 虽然SVD 方法计算步骤简单、操作方便, 但易受数据掺杂噪声的影响, 难以避免病态化矩阵问题.虽然施加阈值约束等策略可有效降低分解矩阵的病态化程度[28], 但大部分情况下, 其解矩阵依旧受噪声干扰严重, 且存在部分不具备水文地质意义的畸变元素, 严重影响后续w 及 T2拟合精度.
针对以上问题, 本文首先介绍了地面MRS 自旋回波正演建模过程, 推导了其灵敏度核函数及正演公式.再基于Grunewald 等[19]提出的 T2反演框架, 总结了地面SE 反演策略.针对SVD 法病态化严重、精度低等问题, 提出将高效、自带非负约束的同时迭代重建技术(simultaneous iterative reconstruction technology, SIRT)作为SVD 的后续处理步骤[29], 提高地面MRS 数据解释精度.本文研究成果将进一步推动SE 探测在地面MRS 领域的应用, 并促进相关正演建模及反演解释方法的进步.
2 地面磁共振横向弛豫探测原理
2.1 传统地面磁共振探测原理
地面MRS 探测利用地下水中氢原子核的自旋现象, 其旋进角频率(拉莫尔频率)由 B0决定[9]:

其中, ω0=2πf0, γ 为地下水中氢原子核的磁旋比.所有原子核的自旋行为形成微量的宏观磁矩M,其幅度表示为 M0.为探测地下水存在, 应用布设于地表的线圈发射激发脉冲, 氢原子核吸收脉冲能量而进入激发态, M 的旋转轴逐渐偏离原方向.此时, M 垂直于 B0方向分量被称为激发横向磁化强度:

激发场停止后, M 以角频率 ω0旋进并回到激发前状态(平衡状态), 释放对应频率交流场, 即为MRS 信号.在该过程中, 通常用 T1(纵向弛豫时间)、 T2等参数描述氢原子核的恢复平衡态过程(弛豫过程).T1与 T2分别为M 平行(纵向)、垂直(横向)于 B0分量, 其恢复初始平衡状态时间, 通常被认为与地下水的孔隙度、渗透率有关.
2.2 地面磁共振横向弛豫探测发展
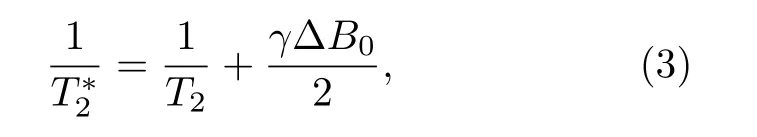
其中, Δ B0为地磁场不均匀程度.在均匀地磁场条件下(地下不存在铁磁性介质), (3)式第二项可忽略不计,可近似替代 T2.但当地磁场不均匀情况下, (3)式第二项的存在会导致远小于 T2.此时直接应用探测值代替 T2, 不仅使探测难度进一步增加(受仪器死区时间影响, 信号越短接收越困难), 而且估测的地下孔隙半径将远小于真实情况.
近十年来, MRS 领域高效充放电及多脉冲发射技术逐渐发展成熟, 为基于SE 信号的 T2探测提供了条件.通常, 地面SE 信号探测有两种方式: 多组不同时间间隔的双脉冲探测序列组合和多脉冲连续发射的CPMG 序列.对于前者, 要求针对同一激发脉冲, 在其关断后设置不同时间间隔的重聚脉冲.接收并拟合多个SE 信号包络峰值, 即可通过数据解释获得地下 T2分布.由于每次测量均需要对同一激发脉冲矩求取其不同时间间隔下的SE信号, 所以该种探测方式效率较低(探测时间是传统FID 实验的数倍).相比于双脉冲组合序列,CPMG 序列(图1)由单个激发脉冲与相同时间间隔的多个重聚脉冲组成, 通过单次间断发射, 即可获得多重SE 信号.其过程为: t =0 时发射激发脉冲q, 激发地下水中氢原子核产生磁共振现象, 形成衰减时间为的FID 信号; t =τ,3τ,5τ,··· 时刻分别发射相同大小的重聚脉冲2q (大小为激发脉冲2 倍), 即可接收在 t =2τ,4τ,6τ,··· 时刻达到峰值的多重SE 信号.针对不同探测层深, 分别发射对应该深度的CPMG 序列(激发脉冲不同), 最终完成整个区域内的地下水探测.相比于双脉冲激发方式, CPMG序列极大提高了探测效率, 进一步推动了相关理论及解释算法的发展.

图1 地面磁共振CPMG 序列激发示意图(为获取包含T2 衰减信息的完整SE 信号, 发射激发脉冲q, 并间隔时间τ 重复发射多个重聚脉冲2q, 重聚脉冲间的间隔为2τ)Fig.1.Typical time diagram of CPMG apply in surface MRS.Measurement for excitation pulse moment q requires a set of refocusing pulse 2q repeating for a defined 2τ delay after the first τ delay and obtains a complete SE response to determine the T2 decay curve.
需要注意的是, 受地下水扩散现象影响, 通过MRS 自旋回波探测得到的横向弛豫时间也不是完全等同于真实横向弛豫时间 T2.具体来说, 将前者定义为 T2MRS, 则[25]:
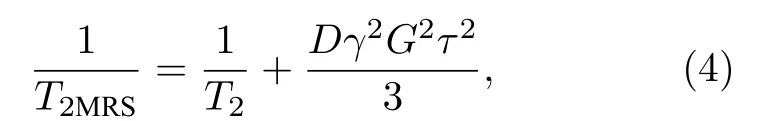
其中, D 为孔隙内填充流体(地下水)的扩散系数, G为空间磁场(地磁场)梯度.为尽量缩小忽略(4)式第二项对探测的影响, 宜选取较小的 τ 值, 以保证探测到的 T2MRS更接近 T2.在本文中, 由于该关系与主体研究内容无关, 故默认 T2MRS=T2, 且下文统一用 T2代替 T2MRS表述地面MRS 探测得到的横向弛豫时间.
3 地面磁共振横向弛豫正反演理论
3.1 灵敏度核函数及正演计算
如前文所述, 氢原子核受激发后章动能够释放交流弛豫信号.对应于不同激发脉冲q, 其MRS 信号响应可描述为[9]
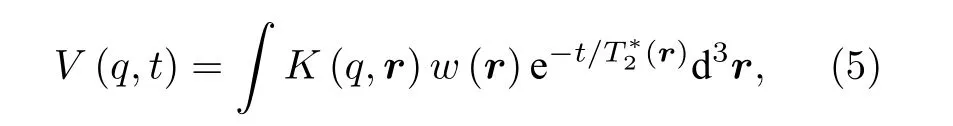
式中, w (r) 为对应于地下位置r 处的含水量;K(q,r)为MRS 的正演灵敏度核函数,
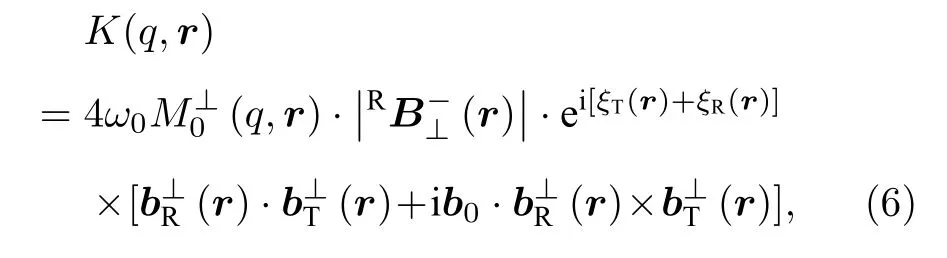
与FID 建模方式不同, SE 信号的横向磁化强度计算还需充分考虑多个重聚度脉冲带来的影响.参考磁共振测井的直接建模理论[32], 地面MRS 自旋回波的激发横向磁化强度可以表示为[17]
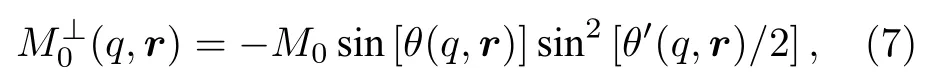
其中, θ′为重聚脉冲形成的扳倒角.考虑到通常CPMG 的重聚脉冲设定为对应激发脉冲的两倍,则SE 信号扳倒角 θ′=2θ , (7)式可简化为
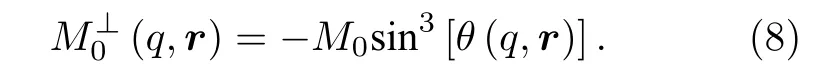
为对比FID 与SE 探测区别, 验证重聚脉冲对激发过程的影响, 计算了同一配置下, 两种激发方式的横向磁化强度分布(发射、接收线圈均为边长100 m 方形、单匝), 结果见图2.由于采用同一激发脉冲(2 A·s), 二者的横向磁化强度分布趋势相似, 但在效率上, 由于SE 信号接收发生在FID 信号之后, 其理论幅值明显低于FID 信号.在上述结果基础上, 仿真二者的一维灵敏度核函数, 即分别将横向磁化强度(2)式、(8)式代入灵敏度核函数表达式(6)式, 并按层状大地结构积分, 如图3(a)和图3(b)所示.由图可知, 对应于横向磁化强度分布, SE 信号的灵敏度核函数幅值也相对降低.
由于SE 信号形式较为复杂(包含多种不同状态氢原子核自旋散相过程), 难以通过固定公式精确定义其包络, 通常仅定义其包络峰值.根据(6)式计算SE 信号灵敏度核函数, 则层状含水结构(一维)下, t =0 时刻(即激发脉冲关断瞬间)开始接收的第n 个自旋回波包络峰值为
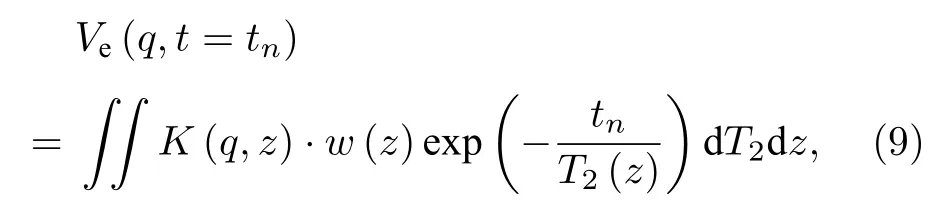
其中, z 对应于一维大地层深, tn为第n 个SE 信号达到峰值的时刻.图4 为典型含水结构下的FID 与SE 磁共振响应(地下8—20 m 存在单一含水层, 含水量最大30%, 对应或 T2为400 ms).由于对应SE 信号(图4(b))的灵敏度核函数整体幅度偏低, 且随着接收时间增大幅度逐渐衰减, 所以对应于同一含水模型其整体幅度明显低于FID信号(图4(a)), 且伴随每一次重聚脉冲发射, 呈现多峰值分布.值得注意的是, 图4 仿真中认为含水层= T2, 根据前文的(3)式, 实际情况下的应略小于 T2, 但由于此处仅用于对比FID 与SE响应形式、量级上的差别, 故并没有严格区分二者间的大小.
为对SE 信号进行线性空间反演, 建立相应正演形式如下:
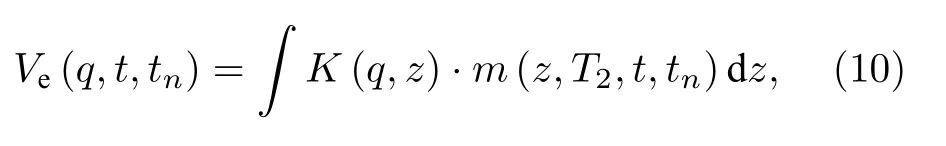

图2 2 A·s 激发脉冲下的地面磁共振(a) FID 与(b) SE 激发横向磁化强度分布剖面(实验配置为100 m 方形发射/接收线圈, 单匝; 填充颜色表示激发横向磁化强度相对于总磁化强度比例)Fig.2.Excitation profile (2 A·s) for (a) FID and (b) SE responses in a surface MRS case with 100 m square transmitting/receiving loop, 1-turn configuration.Color indicates the amplitude ratio of the excited transverse magnetization to the total magnetization.

图3 单匝100 m 方形发射/接收线圈探测配置下的地面磁共振(a) FID 与(b) SE 一维灵敏度核函数(填充颜色反映在对应于激发脉冲矩, 某一固定深度下存在地下水能够诱发得到的磁共振信号幅度)Fig.3.Comparison of kernel function with 100 m transmitting/receiving square loop, 1-turn configuration for (a) FID and (b) SE excitation.Color reflects the signal amplitude induced by underground water at a given depth layer corresponding to each pulse moment.

图4 单匝100 m 方形发射/接收线圈探测配置下, 同一含水情况下的地面磁共振响应(a) FID 与(b) SE 信号(填充颜色反映对应激发脉冲矩, 其FID 或SE 信号随时间衰减的磁共振信号幅度)Fig.4.Comparison of forward responses for the same aquifer distribution, with 100 m transmitting/receiving square loop, 1-turn configuration for (a) FID and (b) SE excitation.Color reflects the signal amplitude induced by underground water decays with receiving time corresponding to each pulse moment.
式中, m (z,t,tn) 为 对应于 Ve(q,t,tn) 的自旋回波变换结果, 也是反演要求解的量, 此处称为地下水SE信号, 包含了最终要求取的w 与 T2信息,
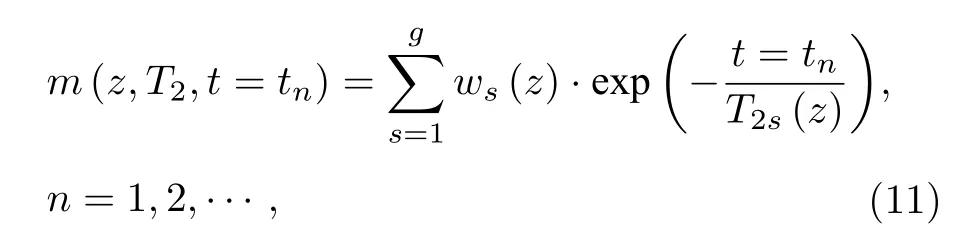
其中, s =1, 2, 3,···, g 为多种弛豫分量对应序号,ws(z) 与 T2s(z) 分别代表单一岩性孔隙物质局部含水量及横向弛豫时间.
3.2 反演策略
将(10)式离散为

即为反演求解的矩阵形式.其中, Iq, Iz与 It分别为脉冲矩、大地层数及信号时间采样点.由于K 与Ve均为复数域矩阵, 为使通过m 矩阵求取的w, T2信息具有实际意义, 通常对K 阵进行雅克比变换[30].通过SVD 方法, 将变换后的灵敏度核函数矩阵分解为

其 中, U 与D 为 正 交 矩 阵,S =diag[s1,s2,··· ,sI,0,··· ,0], I =min(Iq,Iz)为对角矩阵, 包含了奇异值信息.则矩阵(12)式的解为

由于奇异值分解过程中, 奇异值矩阵S 存在不同程度的病态化, 所以通常在上述求解过程中,还需引入合理的截断方案.本文中, 引入Müller-Petke 与Yaramanci 在地面MRS 分辨率计算中采用的滤波法[33], 即应用奇异值结合正则化参数构建对角矩阵 F =diag[f1,f2,···,fI] , 作为滤波系数矩阵, 对S 进行预处理, 则第i 个滤波因子 fi可表示为
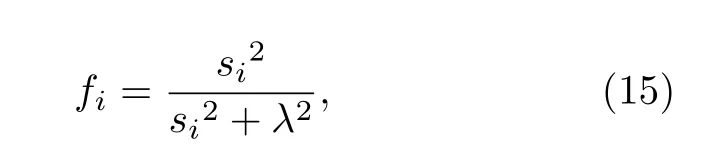
其中, λ 为正则化参数.则此时通过SVD 分解求得的矩阵(12)式解为
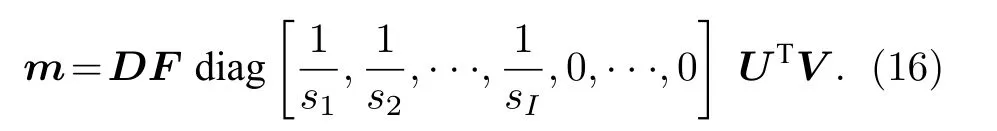
在正则化参数选择过程中, 通常引入偏差度准则等方案, 采用环境噪声水平等因素判断当前正则化参数 λ 是否合适.即便如此, 由于实测数据中环境噪声难以被完全压制, 残留的噪声将进一步加剧SVD 分解病态程度, 并直接影响反演精度.图5显示了相同含水模型(图5(a), 地下8—20 m 存在单一含水层, 含水量最大30%, 对应T2为400 ms),在不同残留环境噪声情况下的SVD 反演结果.可以得出结论, 当原始数据中无噪声残留时(图5(b)),SVD 方法的整体反演效果较好, 除末期数据由于SE 信号衰减幅度较低, 出现轻微误差外, 基本还原了真实的模型.但当原始数据中存在噪声残留(图5(c), 3 nV 高斯白噪声), 尽管噪声残留较小,依旧会明显影响反演结果, 且随着噪声残留增大,其反演结果受干扰情况更加明显(图5(d), 6 nV高斯白噪声).

图5 (a)模型与其在(b)无噪声, (c) 3 nV 及(d) 6 nV 高斯白噪声情况下的SVD 线性空间反演结果Fig.5.(a) Simulated modeling and its linear spatial inversion results employing SVD with (b) no noise, (c) 3 nV and (d) 6 nV Gaussian noise.
由于SVD 反演精度有限, 为进一步提高求解质量, 引入SIRT 方法作为SVD 的后续处理步骤.SIRT 作为代数重建技术[34]的改善算法, 被广泛应用于磁共振测井数据的 T1, T2谱解释[29], 其不仅操作简单、自带非负约束, 且具有优越的收敛特性.但由于该方法对初始模型要求较高, 所以单独使用时并不稳定.而将SVD 分解得到的反演解, 作为初始模型 m(1)代入SIRT 运算, 即可为SIRT 运算提供稳定的初始解, 又可优化SVD 反演结果, 能够进一步提升地面MRS 解释精度, 其具体过程如下.
首先, 认为由初始模型 m(1)得到的模拟数据V(1)与实测数据Vobs差值, 完全由 m(1)与真实地下自旋回波间误差造成, 则根据(12)式可得

将上述矩阵按照时间采样点t=tit(it=1, 2,··· ,It)分割成若干方程组:
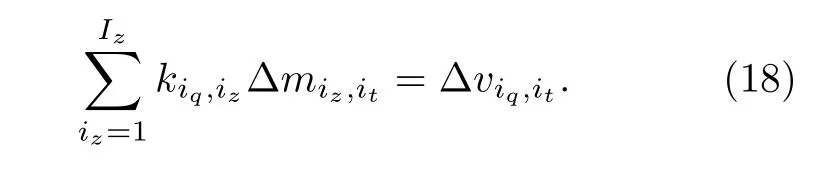
为求解每层地下水自旋回波误差 Δ miz,it, 根据灵敏度核函数确定每层的分配系数:

并 将 信 号 误差 Δ viq,it按照分配 系 数 ρiq, 分配给每层地下水误差 Δ miz,it, 则

通过多次迭代, 不断更新SIRT 求解结果:

其中, j 是当前的迭代次数.随着迭代进行, 拟合与实测数据误差不断缩小, 最终可求得地下水SE 分布矩阵m.
将前文中SVD 反演结果(图5)代入SIRT 进一步迭代拟合, 如图6 所示.可以看到, 对于无噪声情况下的数据反演, SIRT 方法可有效弥补SVD的误差, 其反演结果几乎与原始模型一致(图6(a)).在分别加入3 nV (图6(b))与6 nV (图6(c))高斯白噪声情况下, 单一SVD 方法仅能反演得到前两个地下水自旋回波, 其边缘分辨率极低, 且非含水区域受噪声残留影响, 形成多处明显的波动.对于反演得到的数据尾部, 已几乎难以判定第4、第5自旋回波是噪声残留还是信号.应用SIRT 方法进一步处理上述反演结果, 能够明显提升前两个自旋回波的边缘分辨率, 并识别最末的自旋回波信号,压制非含水区域残留噪声引起的波动.

图6 (a)模型与其在(b) 3 nV 和(c) 6 nV 高斯白噪声情况下的SVD 与SIRT 联合线性空间反演结果Fig.6.(a) Simulated modeling and its linear spatial inversion results employing SVD and SIRT with (b) 3 nV and (c) 6 nV Gaussian noise.
为验证与SVD 联合处理过程中, SIRT 策略的收敛特性, 基于图6 数据计算过程, 同时比较了不同噪声情况下的迭代次数(图7).受噪声波动影响, 含噪声幅度越大, 反演得到的最终数据误差也相应增大, 但收敛所需的迭代次数基本维持不变(约100 次), 这说明了本文提出的策略用于地面MRS 自旋回波反演时, 始终维持着快速收敛的特性.
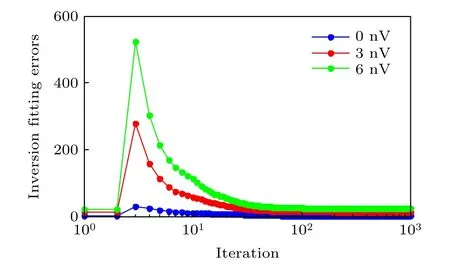
图7 不同噪声情况下, SIRT 线性空间反演迭代次数与拟合误差间的关系Fig.7.Relationship between iteration and fitting errors for SIRT linear spatial inversion with different noise cases.
为得到最终的w 与 T2分布, 单独提取对应于每层的地下水SE 信号包络, 并结合其峰值信息,进行单指数或多指数拟合.为了降低原始数据中残留噪声及求解误差对拟合的影响, 在上述拟合过程中, 通常还需考虑加入窄时间窗, 即分别以t=2τ,4τ,6τ,···时间点为中心, 取一定范围内包络幅值平均量作为拟合峰值, 其过程如图8 所示[19].
4 实验验证
为评价本文方法的有效性, 本节通过模拟实际野外的CPMG 探测实验, 获取对应SE 信号响应,并对该信号进行反演, 最终求得地下w 及 T2分布.

图8 地面磁共振SE 信号线性空间反演及含水量-横向弛豫时间分布拟合示意图Fig.8.Schematic diagram of linear spatial inversion and non-linear fitting of water content and transverse relaxation time for surface MRS spin-echo responses.
4.1 仿真实验设置
虽然SE 探测主要应用在非均匀地磁场分布情况下, 其地下电阻率与拉莫尔频率分布并不均匀.但本节的仿真实验目的为验证本文反演方法有效性, 故可忽略以上非均匀性带来的影响.设定地磁场强度为54721 nT, 拉莫尔频率(即设定的激发频率)为2330 Hz, 地磁倾角与地磁偏角分别为60°, 0°.探测线圈采用边长为100 m 的方形线圈,发射与接收均为单匝, 探测空间为线圈正下方(地下)电阻率为100 Ω·m 的均匀半空间.由于SE 信号的探测激发效率略低于FID, 由此设定反演最大深度为60 m, 激发脉冲为[0.1 8]A·s 间按指数取样的40 组交流脉冲, 重聚脉冲为其倍数, 即分布在[0.2 16]A·s 间, 对应每个激发脉冲发射5 次重聚脉冲, 其间隔参数 τ =83 ms.
结合选取的探测深度及激发脉冲矩, 设定分布在—5 m 至—15 m、—30 m 至—50 m 的两个含水层,背景含水量与横向弛豫时间分别设定为1%和0.02 s, 如图9(a).根据该含水模型拟合得到的每层最大w 分别为30%和50%, 对应 T2为0.4 s 和0.5 s.考虑到选取的参数 τ 及重聚脉冲个数, 设定模拟信号的采样时间为0.8 s.由于野外MRS 探测数据信噪比通常较低, 即使经过硬件及算法多重噪声压制策略, 依旧残留部分噪声.为给实际的野外勘探提供参考经验, 同时验证本文反演方法的抗干扰特性, 向模拟数据中加入3 nV 的高斯白噪声, 则根据上述含水模型计算得到的加噪MRS 信号包络,如图9(b)所示.由于本文为仿真实验, 且其探究重点是SE 信号的建模过程及反演解释, 故信号响应图中没有展示激发脉冲所引起的FID 信号.但在实际野外的SE 探测实验中, 不仅能够在MRS数据初始段观测到FID 信号, 且在后续SE 信号解释前, 还需首先排除接收FID 信号对SE 包络提取的干扰.
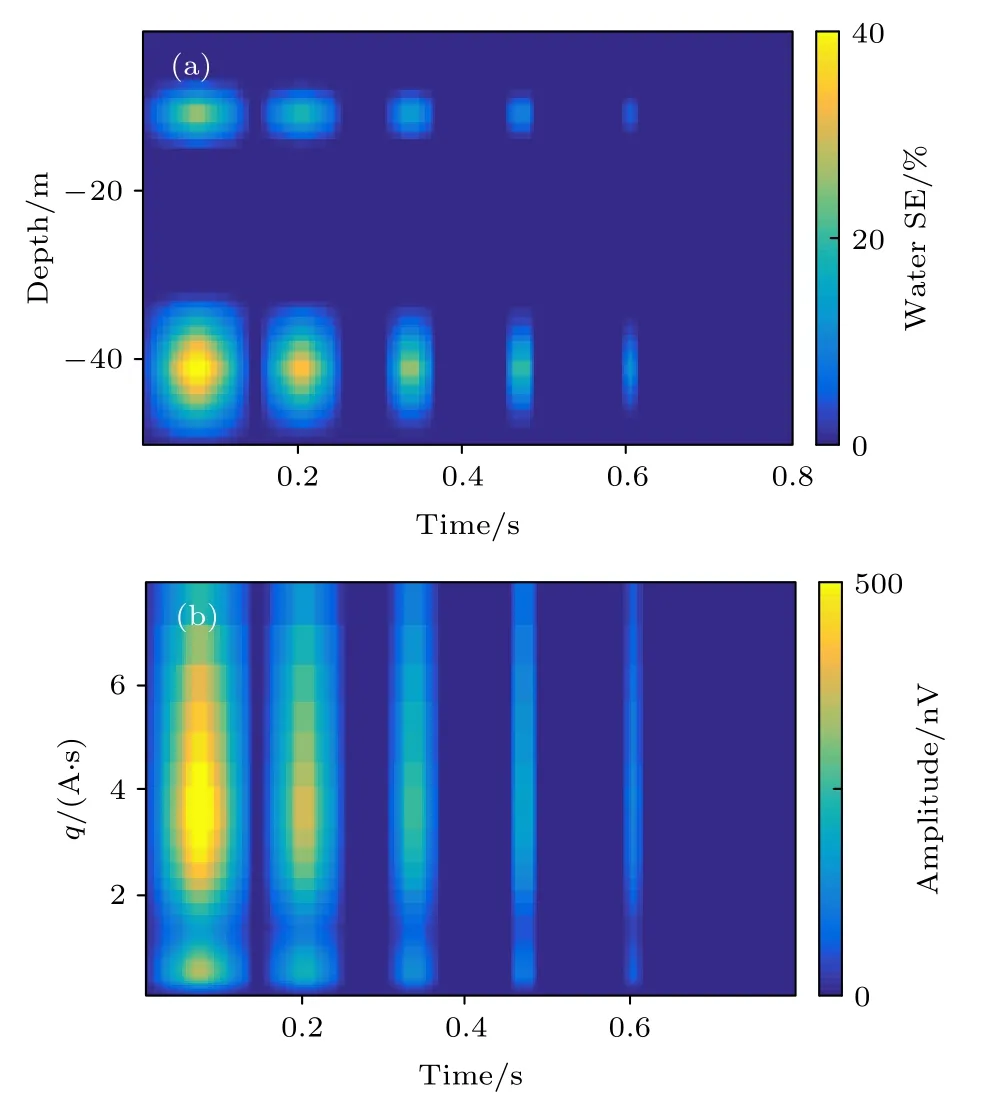
图9 (a)地面磁共振CPMG 探测实验模型与(b)正演数据(加入3 nV 高斯白噪声), 假设地下存在两个含水层, 分别分布在—5 m 至—15 m 及—30 m 至—50 m.Fig.9.(a) Simulated modeling and (b) dataset (adding 3 nV Gaussian noise) for CPMG sequence assuming a surface MRS experiment with two aquifers, which distributed from —5 m to —15 m and —30 m to —50 m, respectively.
4.2 反演结果
作为对比, 仿真数据首先由SVD 方法单独处理.前文提及的吉洪诺夫正则化及滤波器截断方案被应用于该反演过程.为保证反演结果具有实际水文地质意义, 将病态矩阵导致的m 矩阵负值元素,均用零替代.如图10(a)所示, 经过反演过程, SE响应由时间-脉冲间的函数关系转换为时间-深度间函数关系.在噪声影响下, 地下水SE 信号成像质量较差, 甚至在地下12 m 左右出现“断层”, 尽管能够通过该反演结果大致判断两含水层存在位置,但各个地下水SE 信号边缘分辨率较低.尤其对于深层含水层, 其各个SE 的幅度远低于真实情况,且几乎无法分辨含水区域与非含水区域的界限.此外, 在模型中并不存在地下水区域, 均分布着明显噪点, 且在地下20 m 处, 出现2 m 左右的“假”含水层.
由于原模型并不存在多弛豫分量情况, 故仅通过单指数对图10(a)中地下水SE 信号进行拟合(15 ms 时间窗), 得到w 及 T2结果如图10(b)以及图10(c)所示.对比原始模型拟合结果, 仅通过SVD 反演能够相对精准地求得第一个含水层的含水量信息, 但由于浅层m 矩阵中大量噪点的存在,由其拟合得的 T2几乎毫无规律, 第一个含水层对应的 T2信息几乎被淹没.在地下20 m 处, 由于m 矩阵中“假”含水层的存在, 对应含水量与 T2均呈现小范围突变.对于第二个含水层, 虽然通过其w 拟合结果基本能够识别该含水层位置, 但含量远低于真实值, 对应 T2信息也并不准确.在50 m 深度后, 其w 与 T2信息更呈现出完全相反的趋势(含水量随深度降低, T2随深度升高), 与真实情况偏差极大.
应用本文提出的SVD 与SIRT 联合策略处理上述数据, 在经过98 次迭代后, 反演结果基本达到稳定, 如图11(a)所示.正如预期, 联合策略对浅层含水层几乎实现了完全还原, 在深部含水层成像上, 虽然其边缘分辨率稍有降低, 但依旧明显高于SVD 方法单独反演的结果.采用与前文相同手段提取该m 矩阵的w 及 T2信息, 对应结果如图11(b)和图11(c)所示.由于第一个含水层的m 矩阵成像质量更高, 其w 及 T2信息也拟合较好, 几乎与原始模型完全重合, 它们最大误差仅为1.5%和0.02 s.对于深层含水层, 由于m 矩阵中该部分的边缘分辨率略低, 所以对应含水层的边缘部分拟合结果稍有振荡, 但w 与 T2信息基本还原了真实情况, 对应峰值处误差仅为5%和0.08 s.
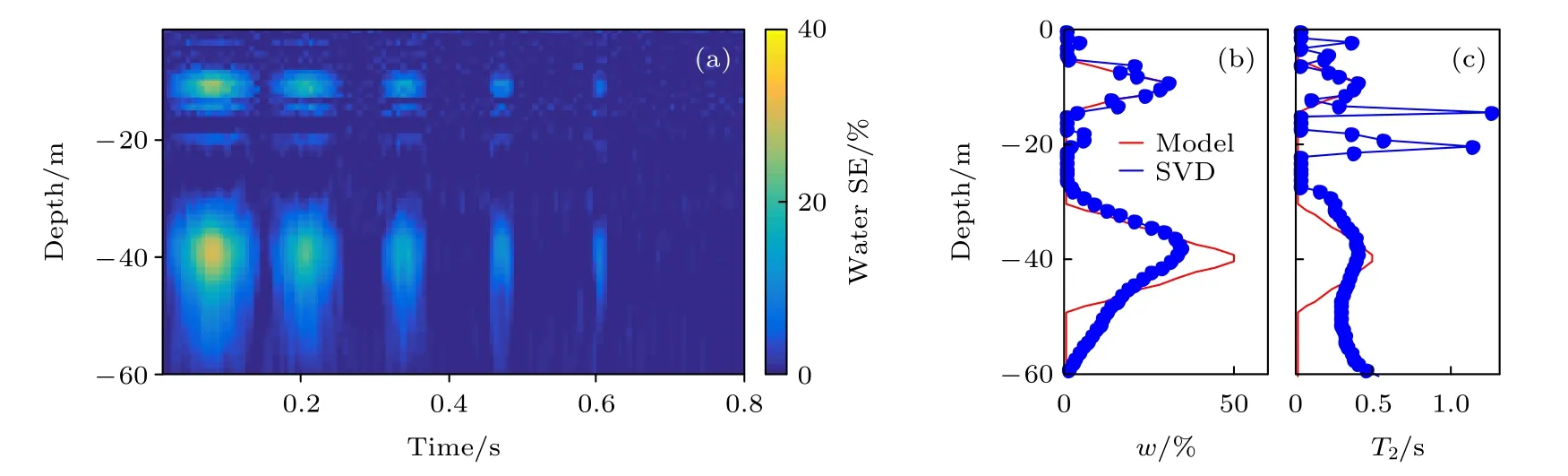
图10 加入3 nV 高斯白噪声的地面磁共振仿真数据SVD 线性空间反演结果 (a) 地下水SE 响应随深度及接收时间的变化;(b)与(c)分别为应用15 ms 时间窗(单指数)拟合得到的w 与T2 分布结果Fig.10.Linear spatial inversion results of SVD method for synthetic surface MRS experiment data with 3 nV Gaussian noise polluted: (a) SE responses of underground water separated as a function of depth z and decayed over time, while the amplitude scale to water content; (b) and (c) are the subsurface w and T2 distribution fitted (mono-exponential) from (a) with a time window of 15 ms.

图11 加入3 nV 高斯白噪声的地面磁共振仿真数据SVD 与SIRT 线性空间反演结果 (a) 地下水SE 响应随深度及接收时间的变化; (b)与(c)分别为应用15 ms 时间窗(单指数)拟合得到的w 与T2 分布结果Fig.11.Linear spatial inversion results of SVD and SIRT method for synthetic surface MRS experiment data with 3 nV Gaussian noise polluted: (a) SE responses of underground water separated as a function of depth z and decayed over time, while the amplitude scale to water content; (b) and (c) are the subsurface w and T2 distribution fitted (mono-exponential) from (a) with a time window of 15 ms.
5 结 论
本文从传统地面MRS 探测理论出发, 系统性介绍并总结了SE 信号正演理论.同时针对SE 信号反演问题, 提出了SIRT 与SVD 算法结合的数据解释策略.该方法不仅能够有效提升解释精度,而且能够避免单一SVD 方法存在的病态化矩阵问题.为了验证本文方法的实际意义, 我们应用加入噪声的模拟数据作为实测数据, 分别用SVD 方法及SVD 与SIRT 结合策略处理上述数据, 取得的反演结果能够精确反映地下真实的含水情况.结合全文理论分析及模拟实验结果, 最终得出以下结论:
1)在地磁场不均匀情况下(地下存在铁磁性介质), 简单的FID 探测并不适用; 应用多脉冲探测序列获得SE 信号, 求解地下 T2分布, 能更准确地判断地下含水层赋水信息; 受探测原理限制,SE 信号激发效率及幅度略低于同种情况下的FID信号.
2)在SE 实测信号解释过程中, 引入磁共振测井相关理论, 能够有效解决其灵敏度核函数计算及正演建模问题; 结合线性空间反演-非线性拟合策略, 可获取其地下w 及 T2分布.
3)虽然直接将SVD 作为线性空间反演策略,也能实现w 及 T2求解, 但其对残留噪声的实测数据适应性较差; 通过SVD 与SIRT 结合, 不仅能够压制前者病态化问题带来的误差, 而且能够有效降低信号残留噪声影响, 提升数据解释精度.
本文的研究成果, 将促进地面磁共振双脉冲及多脉冲仪器, 以及相关正演理论、 T1及 T2反演方法的完善.
6 展 望
本文的正演理论, 主要基于测井领域引入的经验模型.在实际探测中, 自旋回波的激发过程更为复杂, 目前的正演模型仅能算作近似计算.且正如前文提及, 考虑到自旋回波探测的实际应用场合,探测参数的设定及反演还需充分结合地面探测原理, 深入研究脉冲设定、多序列发射时间间隔等问题.需重点探究的是如何在现有仪器能够实现的发射功率下, 尽可能地提高发射电流、缩短发射时间,以降低地磁场不均匀造成的模型误差影响.此外,如何避免激发FID 对SE 信号包络提取影响等问题也需结合具体探测环境、探测参数设置进行解决.综上所述, 在未来的研究中, 我们将进一步考虑模型的优化及野外现场的实用性问题, 为地面磁共振 T1和 T2探测提供方法理论及仪器支撑.
