“力的合成”教学问题剖析

高 嵩 尤洪浩

(山东师范大学物理与电子科学学院，山东 济南 250358)

1 教师的常见教学方式与新教材的差异

在“力的合成”教学过程中,教师通常遵循以下设计思路:首先基于生活情境进行引入,如两个人可一起提起水桶使其静止,而一个人也可将这个水桶提起使其处于同样状态(如图1)．我们称这种“一个力的作用效果与两个或者更多力的作用效果相同”的情境为“等效”情境．

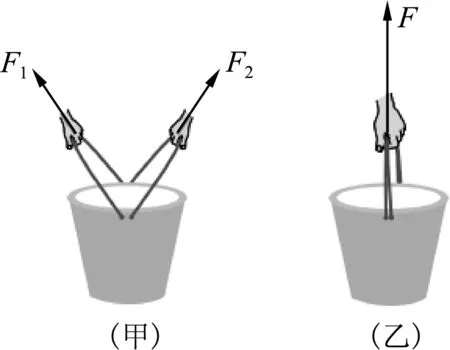
图1 关于合力问题的常见生活情境配图

根据“等效”情境,教师介绍合力的定义:假设一个力产生的效果跟原来几个力产生的效果相同,这个力就是那几个力的合力,那几个力就是这个力的分力．根据分力的情况求合力的过程就是力的合成．介绍定义之后,教师就会基于“等效”的情境设计探究力的合成规律的实验(如图2)．师生如图2(乙)所示测出二力F1和F2的大小,如图2(丙)所示测出作用效果相同的力F的大小,由于F等于F1和F2的合力,因此只需比较3个力的关系就可以证明平行四边形定则．限于篇幅,具体实验过程不做赘述．由此可以看出,教师设定的合力和分力不仅是数值上是相等的,而且都是现实的力,有确定的施力物体和受力物体．

但与教师的解释不同的是，人民教育出版社2019年出版的《普通高中教科书·物理·必修1》表述道:“假设一个力单独作用的效果跟某几个力共同作用的效果相同,这个力就叫做那几个力的合力．……图1中的F等于F1和F2的合力,F1和F2可以看成F的分力．”[1]这种表达告诉我们,当一个力与另外的两个力是合力和分力的关系的时候,它们之间仅仅是数值上等价．当物体在现实世界受到两个互成角度的力的作用的时候,在数值上可以用一个合力来代替．所以合力并不是现实中的具有物质性的力,而只是运算的结果．

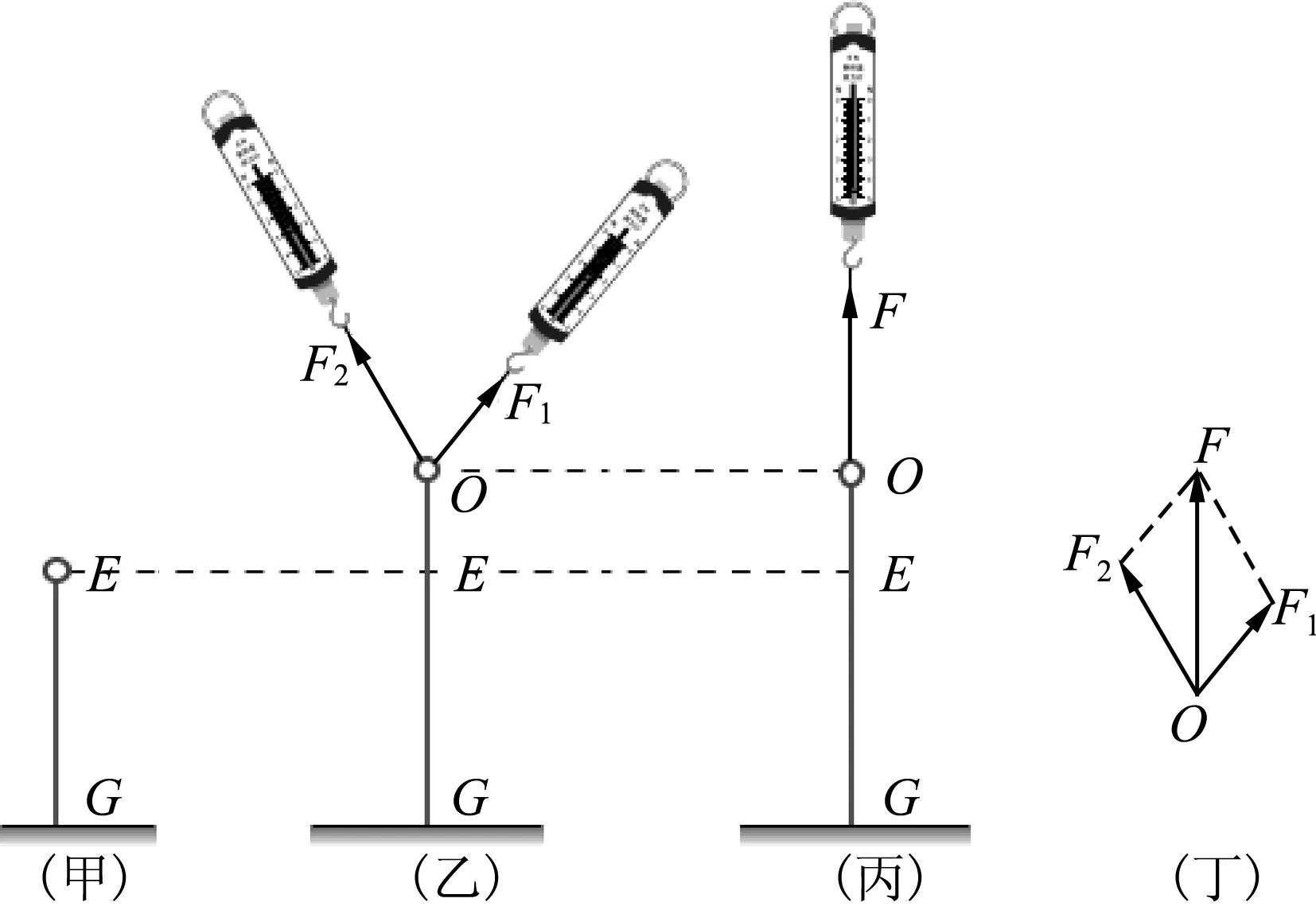
图2 关于合力问题的常见实验配图

那么图1和图2中的F是否是F1和F2的合力呢?有教师认为是,有教师认为不是,还有教师认为无关紧要．但是根据物理课程标准,我们要让学生形成起正确的相互作用观,而对物体进行正确的受力分析是构建相互作用观的一个关键之处,[2]所以我们应该理清这个问题．

2 学生的误解与困惑

现实中的确有些学生在完成了“力的合成”的学习后,也认为在“等效”情境中,与F1和F2共同作用的效果相同的力F就是F1和F2的合力,即合力F就是现实的“等效”情境中的力,有明确的施力物体和受力物体,是实际存在的力,而且可以实实在在地测量出来．有些学生被自己的思路误导,甚至会在受力分析时产生“物体同时受重力、摩擦力、合力”的错误理解．

除此之外,在“力的合成”学习中,学生还经常会对实验产生困惑:当学生拿着橡皮筋、弹簧秤、铅笔进行如图2所示的实验时,由于实验精度的问题,他们会发现按照教师要求把F、F1和F23个力连接起来,常常会得到不等边的四边形关系．对此教师只能生硬地告知学生3个力“应该”是平行四边形的关系．而之后学生利用平行四边形定则得到的F1和F2的合力F合与等效力F常常既不完全共线也不完全相等．这种理论与实践的偏差会导致学生觉得“理论是不对的”或者“实验是没有意义的”,从而导致学生对“力的合成”学习失去动力．

为了让学生突破实验的困惑、让课堂有效进展．本文将对合力、等效等概念的本质进行梳理,并从课标要求及教材的角度分析本节课的教学任务,并给出教学策略．

3 从3个角度对问题进行剖析

3.1 “合力”的本质

新人教版教材明确表示“力是矢量”．因此我们要首先明确合力与矢量的关系,再分析合力是否是实际存在的力．

《牛津物理学词典》对矢量的解释为,一种既有大小又有方向,必须按照矢量运算法则(平行四边形定则)进行计算的物理量.[3]《物理学大辞典》对矢量的解释为“一个同时具有大小和方向的几何对象．”[4]因此力通常用有向线段而非代数表示,而且要计算力时,不能只考虑大小,还必须考虑方向问题．因为有向线段可以自由移动,所以可以把力矢量进行平移,使力的作用点交于一点,便于进一步计算,也就是合成与分解．

那么力为什么需要进行合成与分解?这是因为物体受力情况常常无法直接观测(如火箭升空问题)或比较复杂(如多力平衡问题),要想准确判断物体受力的作用效果,就要对受力情境进行建模,通过一系列的合成和分解的运算计算物体所受的合力．

对于力的合成,皮亚杰在《发生认识论原理》指出,“计算力的合成就是把每个力当作似乎是与别的力无关的向量去进行推论,同时用向量加法把这些力联系起来,这种相加将使这些力全部隶属于一个有确定方向的力的系统．”[5]显然,力的合成是一个数学计算的过程,而且人们在计算时没有囿于力的性质或者施力物体,而是把现实的物理量用抽象的数学量进行表征,把它们视作一个个“有向线段”(数学意义的矢量),把物理系统中的具体关系转译为数学系统中的数理关系,把感知到的现实情境转化成用于计算的抽象领域．恩格斯也在《自然辩证法》指出:“在这里,力进一步被分解,并且被当作复合的东西,因而人们时常会得出新的结果,可是,不要忘记,这不过是头脑中的活动罢了．”[6]

所以,力的合成和分解是“头脑中的活动”,是数学中的矢量运算,描述的是数量关系．当我们说一个力是两个实际的力的“合力”时,指的是矢量运算的结果,合力是抽象概念,不具有实在性．

3.2 “等效”的含义

在“力的合成”教学中,教师经常使用“等效”情境帮助学生认识合力,但也有学生产生“合力F就是现实的‘等效’情境中的力”的错误认识,因此我们要正确认识“等效”的含义．

牛顿曾利用“等效”思想探寻力的合成和分解的规律．在牛顿的《自然哲学的数学原理》中,力的合成和分解规律是三大定律的第一、二条推论:“当两个力同时作用于一个物体时,这个物体将沿着平行四边形的对角线运动,所需时间等于两个力分别沿两边所用时间之和．由此,可以得到以下结论:直接的FAD由任意倾斜的FAB和FBD合成．反之,任意直接的FAD又可以分解成任意倾斜的FAB和FBD,这种合成与分解从力学已得到了充分的证实．”[7]

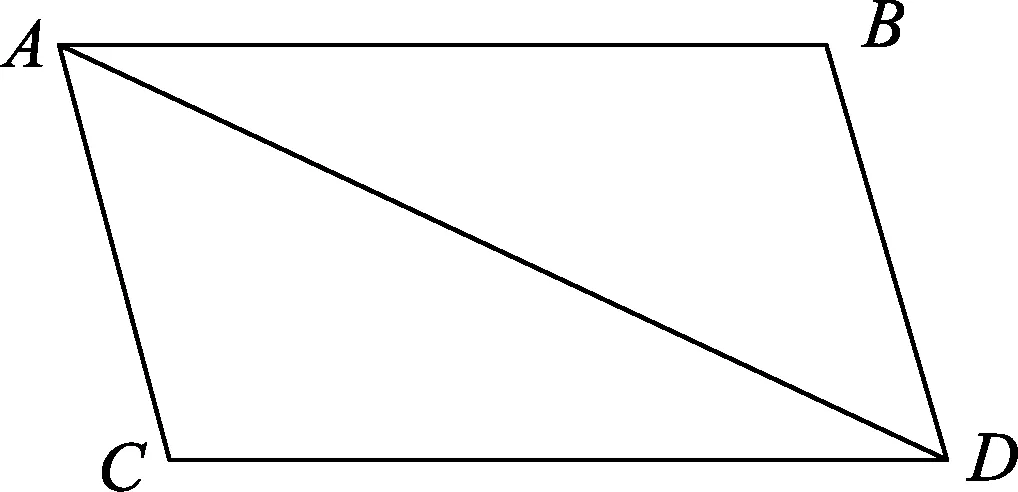
图3 《自然哲学中的数学原理》关于力的合成的配图

牛顿在原文中提到的力FAD就是合力．由上文可以看出,牛顿通过分析物体在不同受力情境下的运动情况并绘图,最终得到结论:力FAB和FBD首尾连接所合成,而力FAD也可以分解成任意夹角的FAB和FBD．这实际上就是力的合成和分解的规律——平行四边形定则的另一种形式:三角形定则．

此后200年的时间里,瓦里翁、伯努利、拉普拉斯等人又对平行四边形定则做了进一步的阐述和证明,[8]维塞尔和哈密顿等人将矢量和复数结合,[9]奠定了矢量理论基础,为平行四边形定则提供了数学依据,最终形成了如今教材常见的平行四边形定则:以有向线段来表示力,长短表示力的大小,箭头表示力的方向,箭尾表示力的作用点,以表示两个力的有向线段为邻边做平行四边形,这两个邻边之间的对角线就代表合力的大小和方向．

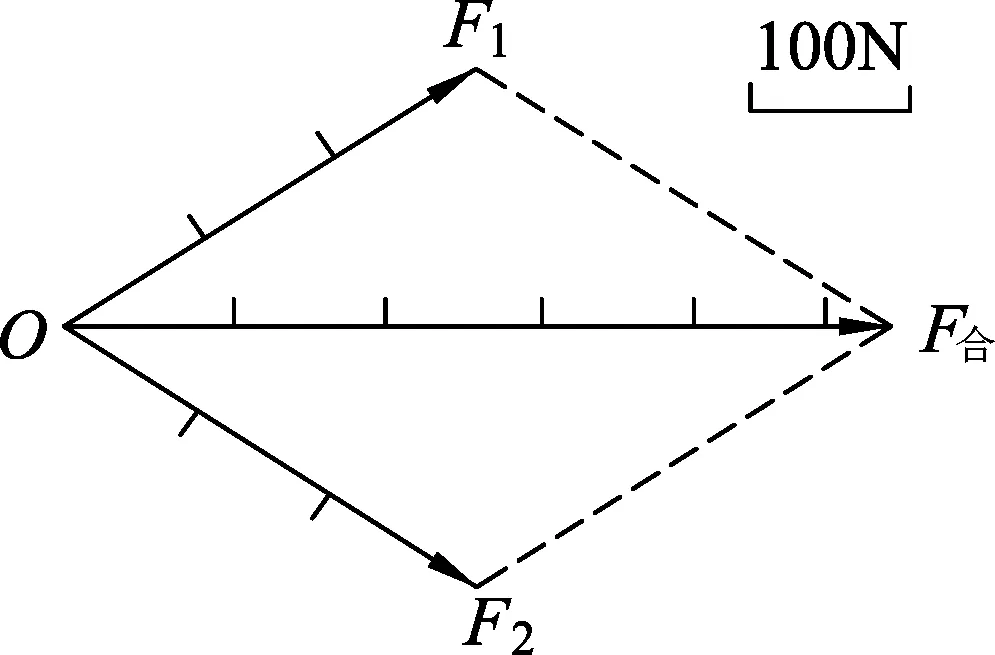
图4 关于平行四边形定则的常见配图

牛顿还在书中补充道:“一般人通常只能通过可以感知的客体来体会这些量(力),除此之外,别无他法,但结果往往会产生一些误解．”[7]这里,牛顿肯定了“等效情境”能帮助人们认识合力,但也表达了对人们可能在“等效”情境中产生误解的担忧．而前面的教学过程恰恰是牛顿担心的课堂表现:把实际施加给物体的、效果上与F1、F2的共同作用相同的F,当成了F1和F2的合力．

那么图1中的F应该如何介绍才是合适的呢?我们可以借助工程力学的“等效力系”概念,[10]用“等效力”和“等效力系”进行表述,把“等效”情境中的F定义为F1和F2的“等效力”,反之,F1和F2为F的“等效力系”．这样一来“等效力”F就是确实存在的力,是我们用来感知“力的作用效果”和“等效替代思想”的工具,是基于数学的力的矢量和(合力)在物理情境中的验证．因此,我们可以用实际存在的“等效力”F来赋予合力以经验的、感性的意义,[11]这也是我们可以设计出实验证明“平行四边形定则”准确性的基础．但如果不能正确解释“等效”情境的意义和“等效力”F的性质,那么就极易导致学生混淆“等效力”与合力．

所以,这属于不同的认知水平，[12]“等效”是帮助我们认识力的合成的方法,在“等效”关系中的等效力与合力并不相同,在教学中应注意区分．

3.3 课标和教材中蕴含的教学思想

在明确了力的合成与等效替代的概念和意义后,我们还需通过剖析课标和教材的具体内容,把握本节课的教学思想,从而实现正确、有效的教学．

《普通高中物理课程标准(2017版)》要求“通过实验,了解力的合成与分解,知道矢量和标量”．[2]可见新课标相当重视“等效替代”实验这类感性认识,力求把物理内容以直观、感性的直接经验(比如演示实验、现象观察)呈现给学生．因此在教学过程中探究实验是不可或缺的一环．

与之相对的,新人教版教材也是基于感性认识展开教学,努力展示插图、实验等感性素材,把合力分力的概念建立在弹簧秤两次被拉到同一位置这种“等效替代”实验上,从“等效替代”实验中概括出平行四边形定则．

但必须注意,基于感性认识固然能让学生容易接受,但如果师生完全沉溺于上述设计思想,在研究抽象概念的时候,还以为自己仍然处在感性认识之中,依旧用客观的感性认知去分析理解主观的抽象概念,如用等效替代的现象去分析力的矢量运算,就极易陷入“经验主义”的错误.[13]典型代表就是本文第2部分提到的一些学生对合力的实在性的误解．

由前文分析可知,图2(丙)的力F是“等效力”而不是“合力”,图4对角线上的力F合才是真正的“合力”．图2证明力的平行四边形定则的实验,其实质是用等效替代的实验替代了矢量相加运算．如果不加详细说明就直接用图2教授平行四边形定则,实际就是忽视了物理感性系统与数学抽象系统之间的区别与联系．这样授课不仅使平行四边形定则更像是实验定律而非矢量运算法则,更是把合力的性质教错了,把“等效力”和“合力”混淆了．

由上述分析可见,新人教版教材之所以采用“假设”“等于”“可以看做”这类词语,就是为了用严谨的措辞提醒师生,避免师生把“等效力”与“合力”相混淆、把“等效替代”实验与矢量运算相混淆,避免产生上文所述的学生误解．

4 分析“力的合成”教学策略

下面我们以新人教版教材“力的合成和分解”一节中“力的合成”部分为例,分析教学策略．

课标和教材都希望教师可以通过实验引导学生归纳现象、认识平行四边形定则,[14]但学生在初中仅接触过共线的力的合成,平行四边形定则涉及互成角度的力的计算,对学生而言很陌生．[15]因此如果教师缺少恰当的策略引导推理、没有让学生较快明确应该努力的方向,学生便会很难“归纳出”教师希望他们理解的规律,也就是对“合力”实在性产生误解、对实验产生困惑．

那么教师该采取何种教学策略,才能既给予学生明确的努力方向,又能保护他们的探究精神,而且避免学生因为实验与理论不符而产生困惑呢?我们认为最适宜的方法就是使用准确而便捷的实验方式,让学生立刻进入正确的物理情境．这样学生能更容易通过情境认识现象,利用实验数据寻找规律．

图5 智能力盘实物图

例如在课上使用朗威DISLab“智能力盘”实验系统,该系统由刻度盘、可旋转的支架、精度高读数简便的力/倾角传感器组成,可以同时测量力的大小和方向,将数据传输到计算机中,因此可以动态显示两个力与合力的平行四边形关系,有助于学生快速分析现象和数据,如图5和图6所示．[16]

图6 智能力盘的配套软件界面截图

在课上,师生通过更精准的“智能力盘”数字化实验系统进行科学探究,利用传感器采集数据,利用计算机处理数据,并进行更深入的讨论．师生先研究两个力与等效力之间的关系,再利用获得的关系计算合力、验证关系;最终总结规律,解释现象,得到平行四边形定则．由于用数字化实验系统测得的数据精确且操作方便,故能帮助学生克服“矢量”概念较模糊的困扰,立刻形成“力的合成”的清晰图景,有利于把物理现实、数学运算密切结合起来;更能避免课堂上出现的许多由于做不准受力图,而探究不出结果的问题．

接下来教师就可以把弹簧秤、橡皮筋等器材交给学生,让学生实际进行操作.[17]这样当他们发现三力并不能构成平行四边形时,就不会怀疑理论错误,而是归因于力的作用线没画准、读数不准确、橡皮筋末端没对齐等误差因素.[18]这样会让学生更加细心地改进自己的实验．而且学生能在这进一步的探索中,更加深入地理解合力的概念、体会矢量和标量的差异、领悟平行四边形定则的普适性．这也体现了课程标准所期望的,让学生通过探究来理解物理原理、体会科学推理的思路．[2]

基于以上教学策略,我们的具体教学过程也就应运而生了.

在课前教师布置任务,指导学生观察生活中的“等效”情境,[19]尽量描述出来．在课上师生首先依托教材中的“力的等效替代”情境,引入“等效替代”,明确“共点力”概念,认识“等效力”;[20]师生从二力分析转到多力分析,发现实际难以寻找等效力,意识到“等效替代”思想在处理复杂受力问题时的局限性,共同探讨对力进行计算的可能性,类比位移的合成,从而引出“力的合成”(力的矢量运算)与“合力”(力的矢量运算结果)概念,并结合教材表述,感受“合力”与“等效力”、矢量合成与等效替代的映射关系;[21]通过智能力盘实验和学生实验学习平行四边形定则,使学生形成正确的“力的合成”和“矢量运算”观念;接下来进一步学习“分力”与“力的分解”概念、学习矢量和标量知识,了解并正确应用平行四边形定则对矢量运算的普适性．

借助上述教学分析和设计,我们就能把现实中的“等效力”和抽象运算中的“矢量和”(合力)对应起来,把物理系统中的“等效替代”关系和数学系统中的“矢量运算”对应起来,让“等效力”成为“合力”的现实映射并进行区分．学生既对等效替代思想有了直观的认识,又能正确理解“合力”的概念,避免混淆．这将有助于学生正确的学习并区分“等效替代”和“矢量运算”,有助于学生形成正确的物理观念．

5 总结与启示

针对“力的合成”教学问题中“合力是实际存在的力”和“合力是‘等效’情境中实际存在的力”的误解,我们通过剖析得到结论:“力的合成”是数学领域的矢量运算过程,“合力”是矢量运算的结果、是抽象概念．“合力”不是实在性的力,而是存在于大脑抽象运算过程中的“矢量和”,要和现实存在的“等效力”区分开．

通过对“力的合成”教学问题进行剖析,我们还进一步得到了两点对物理教学的启示.

(1) 对待教科书要“咬文嚼字”、正确解读．通过本文中分析可见,新人教版教材里的“等于”和“可以看作”等用词别有深意,这说明教材编写者在编写时是非常严谨乃至“字斟句酌”的,所以我们要仔细揣摩教材编写者的良苦用心,以此为基础进行正确表述和教学．比如师生可以从感性材料(教材所示“等效替代”实验)获得“合力”定义和力的合成法则,但如果没有对“等效替代”实验和矢量运算进行区分,那就会导致对“合力是实在性的力还是矢量和”的认识混乱．因此教师在“合力”一节教学过程中既要紧扣课程标准,又要仔细分析教材,对教材内容进行正确表述．

(2) 在教学中应注意要在保护学生探究精神的前提下,尽可能明确地向学生呈现正确的理解方式．比如利用生活中的感性经验带领学生认识“等效替代”思想,通过引入“等效力”概念,让学生顺利区分客观存在的“等效力”和主观抽象的“合力”;通过“用智能力盘探究矢量运算”构建正确的“合力”概念,把“等效力”与“合力”、等效替代性实验与矢量运算进行直观比较,使学生正确认识“等效力”与“合力”的区别与联系,准确理解和接受平行四边形定则,完成本部分内容的学习．

在当前课时少而教学任务重的情况下,作为教师,更应该深入思考物理课教学内容的本质和逻辑,思考课标与教材的编写意图,并选择恰当的教学方式帮助学生实现认识的提升,让他们经历科学探究的过程,通过科学的推理,构建起正确的物理观念,产生科学的态度和情感,从而真正实现物理核心素养的培养．