基于MATLAB的逐点比较法直线插补和圆弧插补算法的研究

陈 雨

（广西大学行健文理学院，广西 南宁 530000）

插补算法是数控机床计算机控制系统中重要的组成部分。逐点比较法是插补中使用最广泛的算法之一，它既可以作直线插补，又可以作圆弧插补，其特点是运算直观，插补误差小于一个脉冲当量，输出脉冲均匀，而且输出脉冲的速度变化小，调节方便。因此，在两坐标联动的数控机床中应用较为广泛[1]。本文分析了第一象限逐点比较法直线插补和圆弧插补的原理，分别给出计算公式和计算过程，最后基于MATLAB编程实现，验证结果。

1.第一象限内逐点比较法直线插补

1.1 偏差计算公式

在第一象限想加工出直线段OA，直线段终点目标A(xe,ye)已知，点m(xm,ym)为加工点，如图1-1所示。

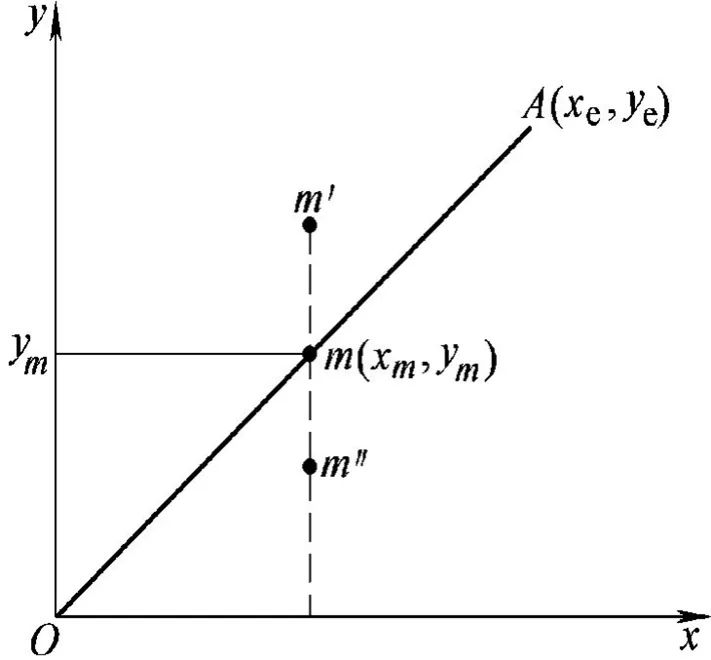
图1-1 第一象限直线

图中直线插补的偏差判别式为

第一象限逐点比较法直线插补的原理是：从直线的起点出发，当Fm≥0时，往+x轴的方向前进一步；当Fm＜0，往+y轴的方向前进一步；当往+x和+y方向所经的步数与规定的终点坐标A(xe,ye)相同时，停止插补。

显然式1-1的偏差计算做了两次乘法，进一步简化偏差计算公式。当Fm≥0时，往+x轴的方向前走一步，xm+1=xm+1，ym+1=ym，该点偏差为

1.2 MATLAB程序实现直线插补计算

直线插补的过程有四个步骤，分别是判别偏差、进给坐标、计算偏差和判断终点。

取第一象限一条直线OA进行加工，起点为原点o(0，0)，终点为目标A(4，5)，步长初值为其中Xe=4，Ye=5，初始偏差值F0=0。

表1-1 计算直线插补

图1-3 直线插补走步轨迹图

2.第一象限内逐点比较法圆弧插补

2.1 偏差计算公式

在第一象限加工逆圆弧AB，已知起点A(x0,y0)，终点目标B(xe,ye)，圆弧半径为R，点m(xm,ym)为加工点，如图2-1所示。

图2-1 第一象限逆圆弧

图中圆弧插补偏差判别式可以定义为

图2-1中逆圆弧段逐点比较法插补原理为：从圆弧的起点A点出发，当Fm≥0时，往-x轴的方向前进一步；当Fm＜0，往+y的方向前进一步；当往-x和+y方向所经的步数与规定的终点坐标B(xe,ye)相同时，停止插补。

式2-2偏差计算做了两次乘法，进一步简化偏差计算公式。

当Fm≥0时，往-x轴的方向前进一步，xm+1=xm-1，ym+1=ym，新加工点偏差为

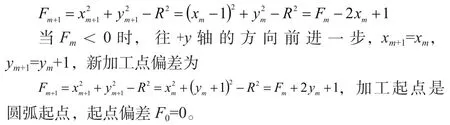
2.2 MATLAB程序实现直线插补计算

圆弧插补的过程有五个步骤，分别是判别偏差、进给坐标、计算偏差、计算坐标和判断终点。

取第一象限一条逆圆弧AB，起点为点A(4,3)，终点为B(5,0)。步长初值为

表2-1 计算圆弧插补

图2-3 圆弧插补走步轨迹图

3.结语

文中给出了逐点比较法第一象限直线插补和圆弧插补的详细计算过程及MATLAB的程序实现并仿真验证。逐点比较法是用阶梯式的折线来无限逼近直线或圆弧等曲线，这种方法与要加工的直线或圆弧的最大的误差仅仅是一个脉冲当量，所以把脉冲当量值尽可能取足够小，便可以达到加工精度要求。