基于动态粒子参数选择的水雾透过率计算

张 弛，吴 鑫，张建奇，李俊儒

（西安电子科技大学物理与光电工程学院，陕西西安710071）

1 引 言

雾是一种发生在大气边界底层的自然现象，它对能见度有重大作用，从而对人类的正常生活产生一定的影响。另一方面，雾会对辐射产生散射和吸收作用，造成辐射衰减，严重影响光电类探测设备的性能，大大降低了目标探测的精准度，容易引起虚警和漏警。因此，研究辐射在雾中的传输特性具有重要的意义，可为雾天气下的光电探测与识别提供理论依据。在以往的研究中［1-3］，通常采用Beer-Lambert定律计算辐射在雾中的衰减，但该方法仅适用于能见度较高的天气状况。对于能见度较低的情况，雾滴粒子对辐射的多次散射作用明显，Beer-Lambert定律的计算结果与实际情况有较大的误差。为了实现辐射在雾中的透过率计算以及传输特性分析，必须考虑多次散射效应的影响，准确地模拟辐射在雾中的传输过程。

目前，常用的介质中辐射传输的计算方法有：辐射传输方程求解法［4-5］和蒙特卡罗法［4，6-14］。辐射传输方程的求解过程十分复杂，需要进行大量的近似简化才能计算出结果，因此适用范围有限［6］。蒙特卡罗法作为一种基于统计学的方法，不需要求解辐射传输方程，而是将辐射在介质中的传输看作大量光子与介质粒子进行碰撞的过程，光子在每次碰撞的过程中会被吸收或被散射，通过统计大量光子被吸收和散射的过程，可以得到较为稳定的统计结果。与辐射传输方程求解法相比，蒙特卡罗法不仅能解决辐射在平面分层介质中的传输问题，还能解决球面介质中的辐射传输问题。由于其自身的灵活性、易实施性和高效性，蒙特卡罗法已被广泛地应用于气溶胶中的辐射传输计算中。

Szymanski［4］等通过蒙特卡罗法和两种基于辐射传输方程的近似算法分析了多次散射效应对气溶胶透过特性的影响。Hassan［7］等和Grabner［8］等分别采用蒙特卡罗法模拟了光在雨和雾中的传输，分析了雨雾的多次散射效应对光通信的影响。Gierstad［9］等通过蒙特卡罗法研究了辐射在海洋气溶胶中的传输。Van Der Laan［10］等利用蒙特卡罗法研究了偏振光在雾中的传输过程，指出与线偏振光相比，圆偏振光在雾中有更大的传输优势。国内也有许多学者采用蒙特卡罗法研究了辐射在雾中的传输特性。王蓉蓉［11］等利用蒙特卡罗法分析了雾天气中太赫兹波和红外波的传输特性，指出相同传输距离下，太赫兹信号比红外信号具有更好的透射能力。王婷［12］等人采用蒙特卡罗法研究了红外辐射在雾中的传输，得到了透过率与传输距离以及能见度的关系。张泽宇［13］等通过蒙特卡罗法对3.8μm和1.55μm辐射在雾中的传输进行了模拟，得到了透过率与传输距离的关系，研究结果表明，3.8μm辐射比1.55μm辐射更适合在雾中进行水平链路的自由空间光通信。张硕［14］等利用蒙特卡罗法对水雾的多次散射进行了模拟，分析了消光系数，水雾浓度以及不对称因子等参数对水雾消光性能的影响，指出提高水雾的浓度并减小粒子半径可有效提高水雾的衰减作用。

以上研究［4-14］均基于Mie散射理论得到粒子群的平均光学参数，并作为蒙特卡罗法的仿真参量，因此光子被散射或被吸收的概率，以及介质粒子的散射相函数在每次碰撞过程中是相同的，这与辐射在介质中的实际传输过程不符。实际上，由于雾滴粒子的尺度大小并不完全相同，研究辐射在雾中的传输问题时，采用动态粒子参数选择的研究方法，可以得到较为可靠的结果。另一方面，蒙特卡罗法需要发射大量的光子来保证计算精度，光子数的增加势必会导致计算时间的增加。研究人员采用Henyey-Greenstein相函数来选择光子的散射方向［6，9-10，13-14］，这会增加蒙特卡罗法的计算时间，降低计算效率。因此，建立一种既符合辐射传输物理过程，又能在不影响计算精度的情况下提高计算效率的蒙特卡罗法具有重要意义。

本文基于传输近似光学参数，提出一种基于动态粒子参数选择的蒙特卡罗法。与传统的蒙特卡罗方法不同的是，该方法采用传输近似光学参数计算光子的碰撞步长、光子被散射或吸收的概率，以及介质粒子的散射相函数；根据介质粒子的尺度分布计算介质粒子与光子的碰撞概率，再根据碰撞概率对传输近似光学参数进行动态选择。选取波长分别为0.85μm和4μm的辐射在4种模式雾（重度平流雾、中度平流雾、重度辐射雾和中度辐射雾）中的传输进行仿真，分析了透过率与传输距离之间的关系，比较了不同波长下透过率的差异，为雾天气下的目标探测与识别等研究提供理论依据。比较了两种蒙特卡罗法的计算时间，为相关工程应用提供参考。

2 多粒子雾层及其光学参数

根据自然界中雾的形成机理和地域，通常将它分为两大类：平流雾和辐射雾。辐射在雾中的传输计算涉及雾滴尺度分布的建模以及光学参数的计算。实际上，作为一种大气水凝物，雾主要由不同半径的水滴粒子组成［6］。因此，本文将雾滴近似为球形水滴粒子。由于复杂的形成和消散过程，不同时间和不同地点的雾滴尺度分布差异很大。本文采用被广泛应用的Gammar模型作为多粒子雾层的雾滴尺度分布模型，同时研究辐射在4种雾（包括重度平流雾、中度平流雾、重度辐射雾和中度辐射雾）中的传输。Gammar雾滴尺度分布模型的表达式为［1］：

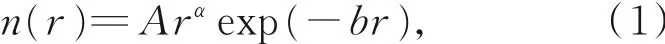
式中：n(r)是单位体积单位半径内雾滴粒子的数量，α，A和b是描述雾滴尺度分布的参数。4种雾的雾滴尺度分布参数如表1所示［15］。

表1 四种雾的雾滴尺度分布参数Tab.1 Parameters for particle distributions of four fogs

图1 为4种雾的雾滴尺度分布。从图中可以看出，辐射雾的雾滴数高于平流雾的雾滴数；与辐射雾相比，平流雾的雾滴数峰值向半径较大的粒子偏移。辐射雾的雾滴数峰值主要集中在5μm附近，而平流雾的雾滴数峰值主要分布在10μm左右。

雾层作为一种半透明介质，雾滴粒子对辐射的多次散射作用不可忽视。对于散射效应较强的介质，即使光学厚度足够小，辐射传输计算仍然非常耗时。因此，为了缩短计算时间，提高计算效率，本文在辐射传输计算中采用传输近似法计算雾层的光学参数，包括传输近似吸收率αtr，传输近似衰减系数Atr和传输近似散射系数μtrs。各参数的计算公式如下［16-17］：

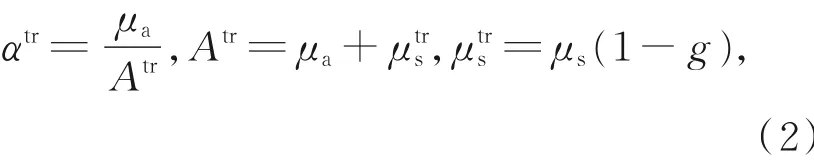
式中：μa和μs分别为粒子的吸收系数和散射系数；g为不对称因子，其取值在[-1，1]。g＞0时表示前向散射，g＜0时表示后向散射，g=0时表示各向同性散射。

辐射在传输过程中会与不同半径大小的雾滴粒子进行碰撞，在每次碰撞过程中，辐射被吸收或被散射的概率以及雾滴粒子的散射相函数会随着与其碰撞的雾滴粒子的改变而变化。为了更加真实地模拟辐射在雾中的传输过程，本文将雾滴粒子的半径划分为多个区间，分别计算不同半径区间内雾滴粒子的光学参数。由于划分的半径区间越多，辐射传输计算所需要的时间越多。出于计算速度的考虑，本文以8个半径区间为例，将平流雾的雾滴粒子半径进行如下划分：0.01～1μm，1～2μm，2～5μm，5～10μm，10～15μm，15～18μm，18～30μm和30～60μm；对辐射雾的雾滴粒子半径区间的划为：0.01～1μm，1～2μm，2～3μm，3～4μm，4～5μm，5～8μm，8～10μm和10～60μm。第i个半径区间雾滴粒子的αtr，i，Atr，i和μtr，is可以表示为：

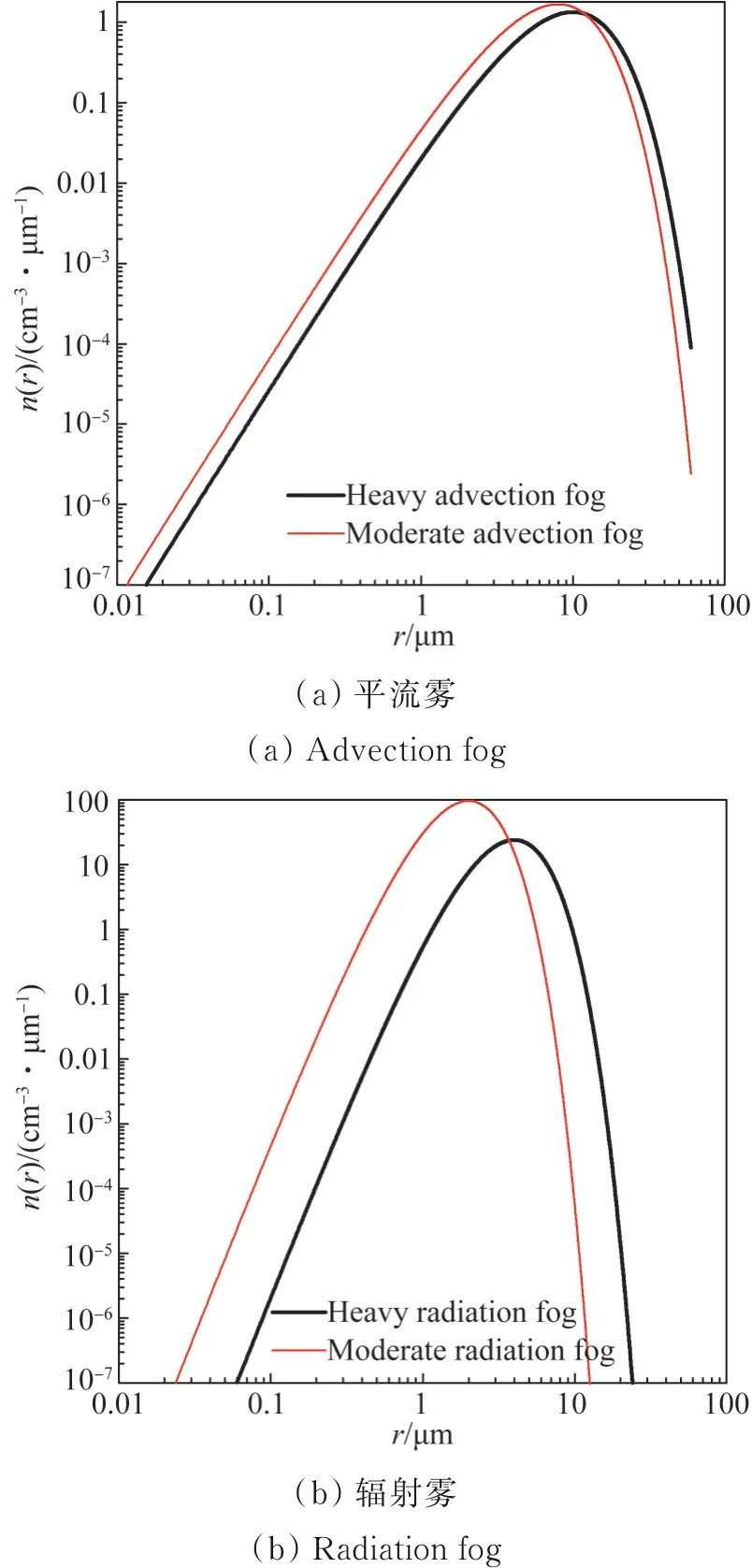
图1 四种雾的雾滴尺度分布Fig.1 Particle distributions of four fogs

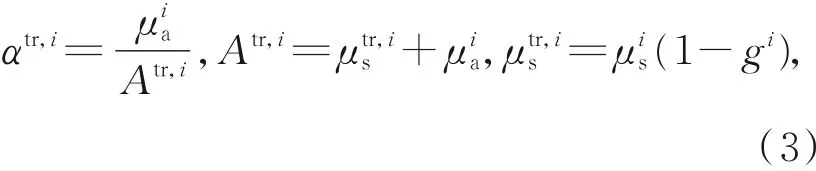
其中：

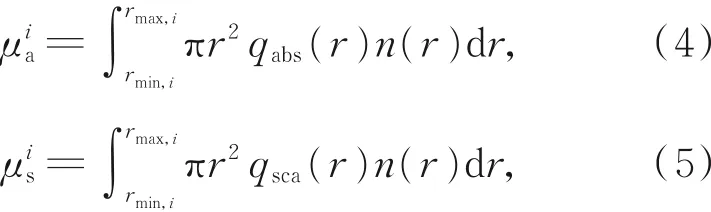
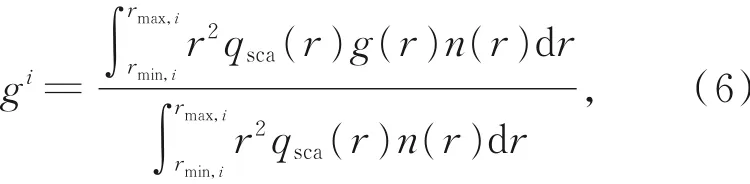
式中：μa，μs和g的定义与式（2）中一致，上标i表示第i个半径区间；rmin，i和rmax，i分别为第i个半径区间雾滴粒子的最小半径和最大半径。单个雾滴粒子的散射效率因子qsca，吸收效率因子qabs和不对称因子g均由Mie散射理论［18］计算得出。图2为λ=0.85μm和λ=4μm时第i个半径区间雾滴粒子的Mie吸收率［18］，αi=μia/(μia+μis)。从图中可以看出，4种雾中的雾滴粒子对0.85μm辐射波的吸收极弱，对辐射的衰减基本是散射效应的作用；与0.85μm辐射波相比，雾滴粒子对4μm辐射的吸收较大，吸收的作用增强，重度平流雾中半径在30～60μm的雾滴粒子对辐射的吸收最大，但吸收率仍然小于0.3，这说明散射的作用仍然比较明显。总的来说，无论是平流雾还是辐射雾，对于0.85μm辐射和4μm辐射，半径为0.01～60μm的雾滴粒子的散射作用比较明显。

图2 λ=0.85μm和λ=4μm时第i个半径区间雾滴粒子的Mie吸收率αiFig.2 Mie absorption probability of fog particles in ith radius region forλ=0.85μm andλ=4μm

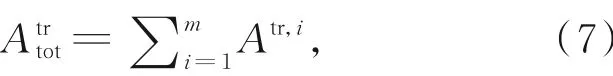
式中m表示雾滴粒子的半径区间数。表2为入射波长分别为λ=0.85μm和λ=4μm时4种模式雾的总传输近似衰减系数从表2中可以看出，λ=4μm时，4种雾的衰减系数高于λ=0.85μm时的衰减系数；与同等程度的辐射雾相比，平流雾的衰减系数较大；同类型雾中，重度雾的衰减系数高于中度雾的衰减系数。为了比较传输近似衰减系数与传统的Mie衰减系数的差异，表3列出了波长分别为λ=0.85μm和λ=4μm时4种雾的Mie总衰减系数比较表2和表3可知，对于λ=0.85μm和λ=4μm的入射波，4种雾的Mie总衰减系数均大于总传输近似衰减系数

表2 λ=0.85μm和λ=4μm时4种雾的总传输近似衰减系数Tab.2 Total transport attenuation coefficient of four fogs forλ=0.85μm andλ=4μm （km-1）

表3λ=0.85μm和λ=4μm时4种雾的Mie总衰减系数Tab.3 Total Mie attenuation coefficient of four fogs forλ=0.85μm andλ=4μm （km-1）

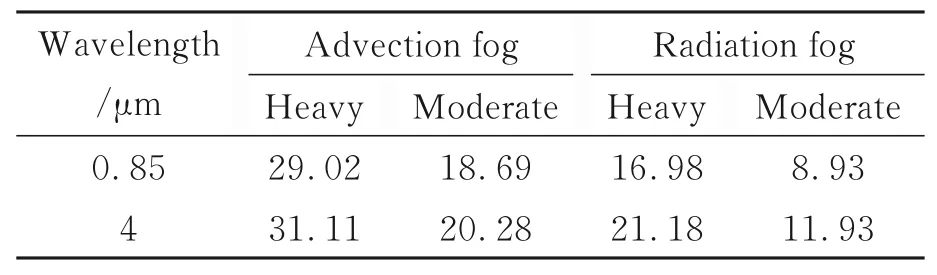
表3λ=0.85μm和λ=4μm时4种雾的Mie总衰减系数Tab.3 Total Mie attenuation coefficient of four fogs forλ=0.85μm andλ=4μm （km-1）

Wavelength/μm 0.85 4 Advection fog Heavy 29.02 31.11 Moderate 18.69 20.28 Radiation fog Heavy 16.98 21.18 Moderate 8.93 11.93

3 散射相函数模型

在辐射传输计算过程中，辐射的单次散射方向由介质中粒子的散射相函数决定。散射相函数的精确度和复杂度直接影响辐射传输的计算结果和计算效率［19］。散射相函数p(θ，φ)用于描述入射能量经粒子散射后的能量角分布，其中θ为散射角，φ为方位角。p(θ，φ)在所有方向上的积分满足［19］：

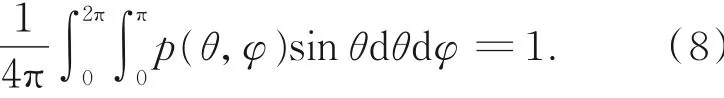
常见的散射相函数计算方法有Legendre多项式展开法，Henyey-Greenstein（H-G）相函数近似法［20］，以及Mie散射理论计算方法［18，20-21］。其中，Legendre多项式展开法和H-G相函数近似法均是对Mie散射相函数的近似。Mie散射理论是均匀介质球形粒子在单色平面波照射下远场散射的精确解，通过Mie散射计算单个球形粒子的散射相函数，可以保证计算的精度。单个粒子的Mie相函数的表达式为［18，22］：

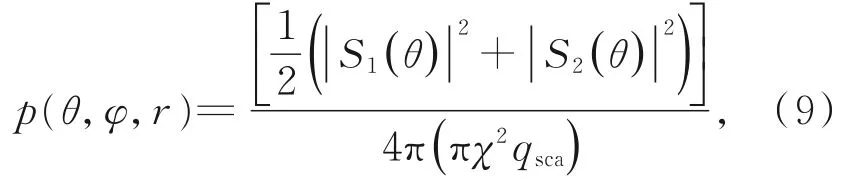
式中：S1(θ)和S2(θ)分别表示垂直极化和平行极化方向的散射振幅函数，其具体表达式参照文献［18］和［22］；χ=2πrn0λ，是粒子的尺度参数，其中r是粒子的半径，λ是入射光波长，n0是介质的折射率。由于球形粒子的对称性，p(θ，φ，r)不会随着方位角的变化而变化。

对于服从一定分布的多粒子雾层，需要结合粒子群的谱分布计算整个雾滴粒子群体系的Mie相函数［19］：

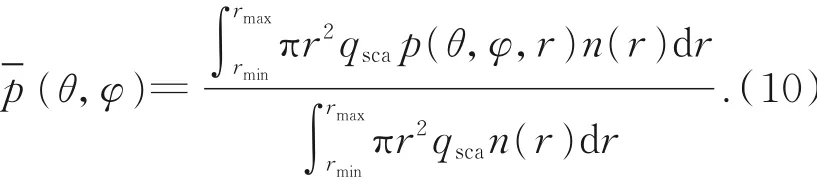
由于Mie散射理论在计算散射相函数时涉及复变量Bessel函数的计算，存在计算时间较长、计算效率低下的问题，因此在辐射传输计算中，通常采用相函数近似法来计算散射相函数。H-G近似相函数由于具有简单的表达式，并且能够求解出散射角随机抽样的概率密度函数，因而被普遍地应用于蒙特卡罗法中。传输近似相函数是一种常用于描述强前向散射特性的近似相函数，由描述各向同性散射分量piso和描述前向散射峰分量pf组成，其表达式为［16-17］：

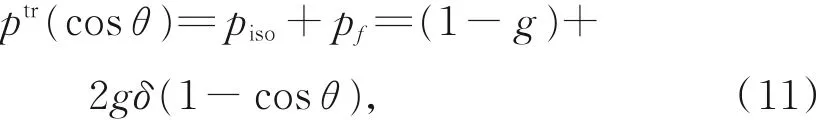
式中：cosθ为散射角余弦，δ是狄拉克函数。图3给出了不同波长下r=8μm的雾滴粒子的Mie相函数、H-G近似相函数和传输近似相函数的分布结果。

图3 不同波长下r=8μm的雾滴粒子的Mie相函数，HG近似相函数与传输近似相函数的分布Fig.3 Distribution of Mie，H-G approximation and transport approximation phase functions of fog particles with r=8μm for different wavelengths

由图3可知：H-G近似相函数与Mie相函数的分布曲线的变化趋势大致相同，但在某些角度下的数值差异较大，表现在两者前向散射峰值均较强，后向散射峰值均较弱，但H-G近似相函数的分布曲线相对平滑，出现差异的原因是Mie相函数是由麦克斯韦方程推导出的解析解，而H-G近似相函数将Mie相函数近似表达为与不对称因子有关的多项式。传输近似相函数与Mie相函数以及H-G近似相函数在数值上存在较大的差异，表现在-1≤cosθ＜1的范围内，传输近似相函数的数值为常数，分布为一条直线，但在cosθ=1的前向散射方向有明显的散射峰，例如当入射波长为0.85μm时，在-1≤cosθ＜1内，ptr恒为0.164；cosθ=1时，ptr=1.836，在θ=0°处的散射能量是在其余各方向上的11.2倍。从式（11）可以看出，传输近似相函数在-1≤cosθ＜1内将散射看作各向同性散射，但在cosθ=1时存在一个散射峰。因此，即使传输近似相函数与Mie相函数存在较大差异，但仍可以用来合理地描述雾滴粒子较强的前向散射特性。文献［23］指出粒子的单次散射分布特性对辐射在多次散射效应较强的介质中的传输特性影响较小。因此，考虑到雾是一种多次散射效应较强的半透明介质，即使传输近似相函数与Mie相函数差异较大，但由于其表达式简单，仍然可以将它应用在蒙特卡罗法中。由于采用传统蒙特卡罗法解决强散射介质中的辐射传输问题存在计算效率较低、耗时严重的缺点，本文为解决计算耗时问题，将不同半径区间内的雾滴粒子的传输近似相函数应用于蒙特卡罗法中来选择粒子单次散射后的方向。第i个半径区间的雾滴粒子的传输近似相函数ptr，i可以表示为：

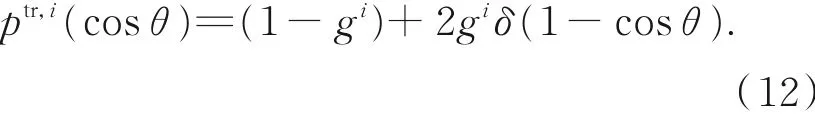
4 动态粒子参数选择模型

基于动态粒子参数选择的蒙特卡罗法计算辐射在雾中的透过率的主要过程如下：以一定的方向发射光子，根据雾的衰减系数确定光子在两个相邻碰撞点的距离；通过雾中粒子的尺度分布和几何尺寸选择与光子进行碰撞的粒子；根据粒子的光学参数确定光子被吸收的概率和光子被散射后的方向（若光子没有被吸收）；根据光子的出射方向和数量计算透过率。该方法与传统计算方法的区别在于：在每一次碰撞过程中，用于计算光子被吸收的概率和光子散射后的方向的光学参数并不完全相同，需在选择与光子进行碰撞的粒子后，再来确定用于计算的光学参数。

图4 辐射在雾层中的传输示意图Fig.4 Schematic of radiation transfer in fog layer

图4 为辐射在雾层中的传输示意图。雾滴的尺度分布在雾层各处均匀一致；辐射的入射天顶角为θin，入射方位角为φin，d为传输距离；被前向探测平面（z=d）收集到的光子即为透过的光子。基于动态粒子参数选择的蒙特卡罗法的具体计算步骤如下：

（1）光子的发射参数设定

每个光子的初始位置为O(0，0，0)，入射天顶角和入射方位角分别为θin和φin。

（2）光子碰撞步长确定

光子在两个相邻的碰撞点之间的随机步长为［6］：

式中：ξ1是0～1之间均匀分布的随机数而在传统的蒙特卡罗法中［6-14］从式（13）可以看出，光子的碰撞步长和雾的总衰减系数有关，总衰减系数越小，光子的碰撞步长越大。

（3）光子与雾滴粒子的碰撞概率计算

光子与雾滴粒子的碰撞概率与雾滴粒子的尺度分布和几何半径有关。雾滴粒子的浓度越高，半径越大，与光子的碰撞概率越大。因此光子与第i个半径区间的雾滴粒子碰撞的概率可表示为：

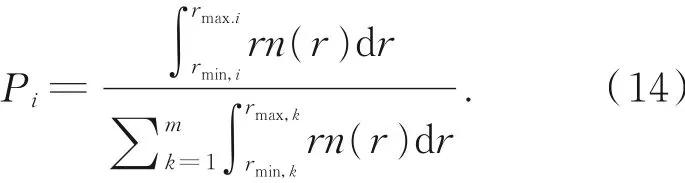
从第1个半径区间到第i个半径区间的雾滴粒子累积碰撞概率为［24］：

当光子移动一个碰撞步长时，通过在0～1均匀分布的随机数ξ2来确定与光子进行碰撞的雾滴粒子。若0＜ξ2≤PC，1，则光子与第1个半径区间的雾滴粒子进行碰撞；若PC，i-1＜ξ2≤PC，i，则光子与第i个半径区间的雾滴粒子进行碰撞。

（4）光子被吸收的概率分析

当确定光子与第i个半径区间的雾滴粒子进行碰撞后，通过在0～1之间均匀分布的随机数ξ3来确定光子是否被吸收。若ξ3≤αtr，i，则光子被第i个半径区间的雾滴粒子吸收，停止跟踪该光子；否则，光子会以新的散射方向继续在雾层中传输。与传统蒙特卡罗法不同的是，在基于动态粒子参数选择的蒙特卡罗法中，αtr，i会根据步骤（3）中选择的第i个半径区间的雾滴粒子进行更新，每一次碰撞事件中的αtr，i不完全相同。

（5）散射方向确定

若光子没有被雾滴粒子吸收，则会被散射到新的方向。将传输近似散射相函数转化为累积概率密度分布函数CPDF(μ)（μ=cosθ），然后采用0～1之间均匀分布的随机数ξ4对CPDF（μ）抽样来获得散射角θ。CPDF(μ)由下式得出［23］：

式中：F(g，μ)是不对称因子g和散射角余弦μ的函数μ，C是传输近似相函数在-1≤μ≤1内积分求得的数值。CPDF(μ)是0～1之间的分布，在步骤（3）中选择第i个半径区间的雾滴粒子与光子进行碰撞后，g和C已知，给定一个0～1之间均匀分布的随机数ξ4，可以通过式（16）得到对应的μ，进而获得散射角θ。方位角φ均匀分布在0～2π之间，其抽样值为φ=2πξ5，ξ5是0～1之间均匀分布的随机数。

（6）透过率计算

从雾层中逃逸并被前向探测器接收的光子即为透射的光子。通过统计透射的光子数量，可得到透过率为［25］：

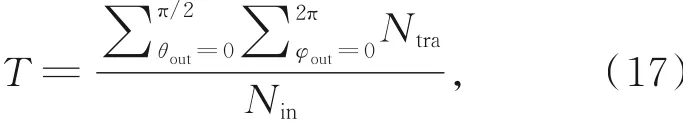
式中：θout和φout分别是出射天顶角和出射方位角，Nin和Ntra分别是入射光子数和透射光子数。

5 计算结果及分析

设定入射波长分别为λ=0.85μm和λ=4μm，光子数为108个，所有光子均为垂直入射（入射天顶角θin=0°，入射方位角φin=0°）。采用两种蒙特卡罗法仿真不同入射辐射在4种雾中的传输：（1）传统的蒙特卡罗方法［6，9-10，13-14］采用Mie光学参数以及H-G散射相函数，以下简称为“HG MC”；（2）基于动态粒子参数选择的蒙特卡罗法，以下简称为“DPS MC”。通过计算不同传输距离下的透过率和计算时间来分析辐射在雾中的传输特性以及蒙特卡罗法的计算效率。

图5 为重度平流雾和中度平流雾透过率随传输距离的变化曲线。由图5可知：随着传输距离的增加，两种辐射波的透过率均逐渐减小，在相同的传输距离下，0.85μm辐射的透过率相对于4μm辐射的透过率更大，表现出良好的透射特性。这与图2中的结果一致，由图2可知，相对于0.85μm辐射，重度平流雾和中度平流雾对4μm辐射的吸收较大，更多的光子被雾滴粒子吸收，使得透过的光子减少；相同传输距离下，两种辐射波在重度平流雾中的透过率更低，这与表2和表3中的结果一致，与中度平流雾相比，重度平流雾对两种辐射的衰减更大。

两种方法对透过率的计算结果具有相同的变化趋势，说明本文提出的DPS MC是可靠的。但由于DPS MC和H-G MC中采用的单次散射相函数不同，以及DPS MC考虑了不同半径区间的雾滴粒子散射特性的差异性，两种方法在数值上不完全一致。两种方法对0.85μm辐射在平流雾中的透过率计算结果差异较明显，对4μm辐射的计算结果则较为接近。当传输距离为150 m时，两种方法对0.85μm和4μm辐射在重度平流雾中的透过率的绝对误差分别为0.048 3和0.001 5。两种方法之间的绝对误差在波长上的差异也是合理的，从表2～表3以及式（13）可知，在重度平流雾中4μm辐射的衰减大于0.85μm辐射的衰减，使得光子的碰撞步长减小，导致透射的光子经历的散射次数更多，而散射次数的增多，减少了散射相函数不同造成的透过率差异，两种蒙特卡罗法的计算结果最为接近。

图5 重度平流雾和中度平流雾的透过率随传输距离的变化曲线Fig.5 Transmittances in heavy advection fog and moderate advection fog as function of propagation distance

图6 为重度辐射雾和中度辐射雾透过率随传输距离的变化曲线。由图6可知，随着传输距离的增加，两种辐射波的透过率均逐渐减小。由图2可知，相对于4μm辐射，重度辐射雾和中度辐射雾对0.85μm辐射的弱吸收作用，使得0.85μm辐射比4μm辐射在雾中具有更强的透射特性。相同传输距离下，两种辐射波在重度辐射雾中的透过率更低，产生这种现象的原因与衰减系数的大小有关。相比于中度辐射雾，两种辐射波在重度辐射雾中的衰减系数更大，使得更多的光子被吸收或者被散射到其他方向，更少的光子透过雾层被探测器收集。此外，对比图5和图6可知，在相同传输距离下，与同等程度的平流雾相比，两种辐射波在辐射雾中的透过率更高，穿透能力更强。

图6 重度辐射雾和中度辐射雾透射率随传输距离的变化曲线Fig.6 Transmittance of heavy radiation fog and moderate radiation fog as functions of propagation distance

图7 两种蒙特卡罗法的计算时间随传输距离的变化曲线Fig.7 Computational time of two Monte Carlo methods as function of propagation distance

图7 为两种蒙特卡罗法的计算时间随传输距离的变化曲线。由图7可知：两种蒙特卡罗方法的计算时间均与传输距离成正比，随着传输距离的增加，计算时间逐渐增大；相比于0.85μm辐射，两种蒙特卡罗法对4μm辐射的计算时间较长。在相同传输距离下，不同波长计算时间的差异主要由衰减系数决定，衰减系数越大，透过的光子经历的散射次数越多，耗时越长，这也是导致两种方法对平流雾的计算时间更长的原因；与H-G MC相比，DPS MC在较长的传输距离下的计算速度有明显的提升，随着传输距离的增加，DPS MC在计算速度上的优势越来越明显。入射波长为4μm时，对d=100 m和d=400 m的重度平流雾H-G MC的计算时间分别为650 s和1 650 s，DPS MC的计算时间分别为610 s和920 s，分别缩短了6%和44%；相同传输距离下，DPS MC对重度平流雾在计算速度上的优势最为明显，当入射波长为4μm，传输距离为400 m时，DPS MC较H-G MC对重度平流雾、中度平流雾、重度辐射雾和中度辐射雾的计算时间分别缩短了44%，33%，37%和23%。

6 结 论

本文建立了一种多粒子雾层模型，该模型中雾滴粒子为半径不同的球形水滴粒子。雾滴粒子半径被分为多个区间，计算了不同半径区间内雾滴粒子的传输近似光学参数。选择0.85μm和4μm两种辐射波以及重度平流雾、中度平流雾、重度辐射雾和中度辐射雾4种雾，采用基于动态粒子参数选择的蒙特卡罗法（DPS MC），模拟了两种辐射波在4种雾中的传输过程，分析了它们在雾中的衰减特性，并将DPS MC的计算结果与传统的蒙特卡罗法（H-G MC）的计算结果进行了比较。结果表明：相比于4μm辐射，0.85μm辐射在雾中的衰减更小，表现出了良好的传输性；相比于同等程度的辐射雾，两种辐射在平流雾中的衰减更加明显；两种蒙特卡罗法的计算结果随传输距离变化的趋势一致，但在数值上不完全相同，多次散射效应越强，两种方法在计算结果上的差异越小；与H-G MC相比，DPS MC可以有效地缩短计算时间，其计算优势在远距离传输以及多次散射效应较强的介质中传输的情况下更加明显。

DPS MC更加真实地反映了辐射在雾中的传输过程，并且能有效地缩短计算时间，为雾中的辐射传输计算提供了新的思路。在后续的研究工作中，将开展不同入射辐射波在不同雾环境下的传输特性试验，进一步探讨雾滴粒子半径区间的划分与DPS MC的计算精度和计算效率之间的关系，以及该方法在相关工程应用上的适用性。