基于离散元的超声波振动辅助TBM 滚刀碎岩分析
2021-03-25韩君鹏赵大军张书磊
韩君鹏,赵大军,张书磊,周 宇
(1.吉林大学建设工程学院,吉林 长春130026;2.黄河勘测规划设计研究院有限公司,河南 郑州450003)
0 引言
在隧道工程施工领域,高强度坚硬岩层是导致施工进度缓慢的一个重要因素,如何高效快速地对坚硬岩石进行有效破碎,是一个普遍关注的研究问题[1-2]。全断面硬岩隧道掘进机(TBM)是长隧道掘进施工中优先采用的专业设备,依靠刀盘安装的滚动刀具滚压破碎岩体,具有施工速度快、成洞质量高、作业连续性好等优点。滚刀在液压油缸压力作用下压入岩石,裂纹随之产生,并随压力的增加而扩展,相邻两滚刀产生的裂纹贯通时,其间的岩石脱落,达到破碎岩体的效果[3]。硬岩地层通常具有较高的强度,此时破坏其所需要的压力降急剧增大,而当地层中石英含量较高时,岩石的研磨性较强[4],刀具在强挤压、高研磨的条件下工作,其损坏失效的速度将大幅度加快,因此在硬岩条件下隧道掘进的进尺速度较慢、刀具磨损较快,大大增加了施工成本[5]。
为了提高TBM 开挖效率,降低施工成本,众多学者相继开展研究提高滚刀的工作效率与使用寿命。部分学者针对刀具磨损机理进行了研究,分析影响刀具功效的诱导因素,试图延长单位进尺长度下刀具寿命[6]。Liu 等[7]通过试验测试发现相同条件下滚刀顺序破岩比双滚刀同时破岩能够形成更大的破岩槽,数值分析显示顺序破岩条件下裂纹贯通效果更好。谭青等[8]、蔡晨晨[9]对比了冲击动载与静载条件下滚刀破岩,发现循环冲击载荷可以促进岩石内部裂纹产生及其在水平方向上的延伸贯通。赵伏军等[10]以花岗岩为对象,研究了压头侵入岩石过程,得出动静耦合加载能大幅提升碎岩效果。
超声波振动是一种超高频率的循环载荷作用方式,能够产生与硬岩固有频率相同或相似的频率[11],在该频率循环载荷作用下,岩石将产生共振现象,发生疲劳破坏[12]。Zhao 等[13]利用热红外无损检测技术对超声波振动载荷下岩石损伤特性进行了探究,认为破坏过程分为弹性变形、微裂缝与屈服、宏观裂纹与破坏3 个阶段。Yin 等[14]通过单轴抗压实验验证超声波振动有效降低了花岗岩的强度。Fernando 等[15]选用3 种岩石进行了旋转超声加工实验,发现超声振动可以降低岩石切削力,且切削速度提高了3 倍。数值模拟方法可以通过计算机软件展示岩体模型在运行过程中的微观损伤及宏观力学参数变化,相对于物理测试更加直观且便于分析,因而在岩石方面的理论研究中得到广泛应用。离散元模拟手段因其在模拟岩石裂纹演化方面的优势备受关注[16-17]。Moon 等[18]基于离散元数值模拟方法分析了滚刀间距与贯入度对应的岩石受力状态,获得了最佳破岩条件。Jiang 等[19]模拟了双滚刀切割岩体,将岩体破碎分为加载阶段、卸载阶段和残余跃变破碎3 个阶段。Li 等[20]建立了楔形滚刀碎岩模型,描绘了细观裂纹扩展与损伤演化过程,分析了不同参数下的碎岩效率。
现有针对提升破岩效率而对滚刀施加的冲击动载频率较低,单次冲击伴随较大的载荷变化,不利于滚刀寿命的保持,对于超高周循环载荷辅助加载尚欠缺研究,离散元模拟技术可从微观角度深入探查岩石内部损伤演化过程,对于揭示超声波振动辅助破岩机理有重要意义。本文采取颗粒流离散元模拟软件构建了花岗岩模型,通过模拟滚刀侵入花岗岩岩体过程,分析滚刀在常规滚动模式下与施加超声波振动辅助碎岩模式下岩石裂纹扩展发育情况,对比滚刀在超声波振动辅助下的破岩效果,为提高滚刀碎岩效率提供新的思路,为超声波辅助滚刀碎岩研究提供理论依据。
1 离散元模型与参数标定
1.1 离散元基本理论
1.1.1 基本原理
Particle Flow Code 是一款基于离散单元模型(DEM)的细观分析软件,在模拟非均质岩石材料动态破坏过程方面有着较为广泛的应用。模型中的每个颗粒是一个具有质量和表面的刚性体,独立运动并可以产生位移和旋转。通过内力和力矩成对产生的接触定义了颗粒间的相互作用方式,并随计算的进行实时更新,识别并产生新的接触。颗粒间的接触是以软接触的方式实现的,刚性颗粒可以在接触点处相互重叠,重叠区域较小,通常视为一点,重叠量的大小通过力-位移定律与接触力相关。颗粒的运动符合牛顿运动定律,墙体的运动由用户指定并不受接触力影响,实现对颗粒的加载或约束。
运算过程采取迭代循环的计算方式,如图1 所示,在确定时间步长的基础上依据牛顿运动定律更新位置与速度,而后更新模型时间,并根据颗粒位置创建或删除接触,最后根据力-位移定律更新接触处的力和力矩,开启下个计算循环。
1.1.2 接触模型
所定义的颗粒间相互作用定律即为一个接触模型。接触的力学行为决定着离散元计算结果的准确性,单个的颗粒、墙体间通过接触产生微观力学行为,相互组织串联,进而由局部影响整体。研究小组采用不同的接触模型设置模型内颗粒、墙体间的接触属性,采用的接触模型类型包括线性模型、线性平行粘结模型、光滑节理模型。
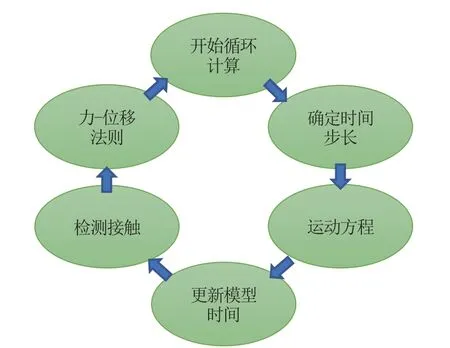
图1 迭代循环计算过程Fig.1 Iterative cycle calculation process
线性(Linear)模型提供了一个无穷小界面的力传递行为,接触力矩为零。接触包括线性和阻尼组件,线性组件控制线弹性摩擦,而阻尼组件控制粘结,线性组件不能承受拉力。
线性平行粘结(Linear Parallel Bond)模型可用于粘结材料的力学行为。该粘结可视为一组具有恒定法向刚度和剪切刚度的弹簧,均匀分布在两颗粒接触一定范围内的矩形平面内。模型产生两个结合组分,一个线性组分,等效于线性模型,另一个称之为平行粘结,与第一个平行作用。线性组分不抵抗相对旋转,粘结组分抵抗相对旋转,因此平行粘结会产生力和力矩,导致产生粘结材料内的法向应力与剪切应力。
光滑节理(Smooth-Joint)模型可以模拟平面界面的剪胀力学行为,无需考虑沿界面分布的局部粒子的接触方向。模型中包含了线弹性、粘结、摩擦膨胀界面的宏观表现。在粘结超出强度极限或断开前,粘合部位具有线弹性的特性,未粘结部位是线弹性和膨胀摩擦,通过在剪切力上施加库仑极限来适应滑移。通过将相互接触的两组粒子设置为该模型,可以模拟摩擦或粘结连接。
不同接触类型的理论表面如图2 所示。

图2 接触理论表面Fig.2 Theoretical contact surface
1.2 岩石模型微观参数标定
为了达到可靠仿真效果,研究小组对花岗岩进行了室内单轴压缩测试,获得了宏观力学参数,并基于此结果采用试错法对模型细观参数进行校准标定。
选用的花岗岩试样是中粒花岗岩,开采自中国吉林省某矿山,试样的主要矿物组成包括长石(0.6~3.0 mm,60%~70%)、石 英(0.5~2.5 mm,20%~30%)、黑云母(0.5~2.0 mm,5%~7%),其他矿物<1%,花岗岩物理力学参数如表1 所示,主要造岩矿物成分力学参数如表2 所示。

表1 花岗岩物理力学参数Table 1 Physical and mechanical parameters of granite
如图3 所示,所构建的单轴压缩花岗岩模型共8818 个颗粒,模型构建中运用了颗粒簇(Cluster)命令,Cluster 是将一些颗粒体通过一定强度粘结在一起,形成一个颗粒组,一个Cluster 内的颗粒粘结可在外力足够大时失效破坏,因此可用Cluster 模拟岩石内矿物晶体。模型总计生成2203 个颗粒簇,每个颗粒簇中颗粒数目不超过7 个,运用高斯函数随机将模型中的颗粒簇指定为石英、云母、斜长石、碱性长石,模型中各造岩矿物组分的比例如图4 所示。
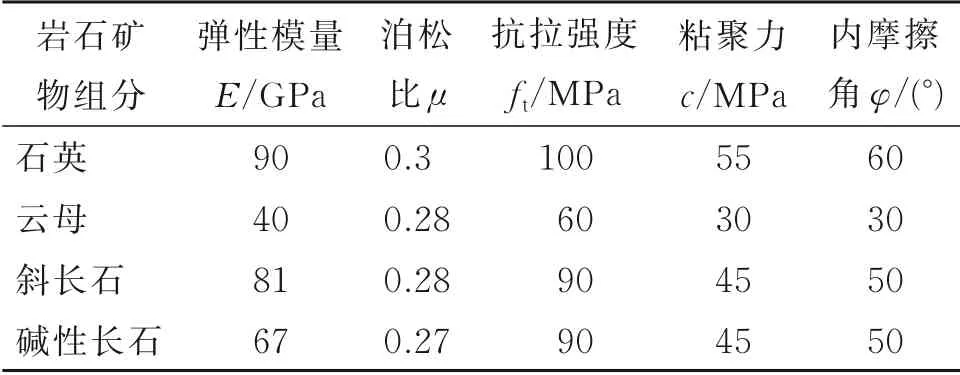
表2 花岗岩造岩矿物力学参数[21-22]Table 2 Mechanical parameters of the mineral components of granite

图3 花岗岩试样及模型Fig.3 Granite sample and model

图4 花岗岩模型造岩矿物比例Fig.4 Percentage of the mineral components of the granite model
模型的接触模型采用混合设置方式,墙体与颗粒间设定为Linear 模型,颗粒簇内部颗粒间采用Linear Parallel Bond 模型粘结,颗粒簇间选用Flat⁃Joint 模型构建粘结关系。矿物晶粒簇间的粘结强度,设定为该交界面相邻两矿物中最小粘结强度的60%[23-24]。模型采用的力学参数如表3~5 所示。
单轴压缩室内试验以及离散元模拟均以Ø35 mm×70 mm 花岗岩模型为研究对象。宏观力学数据与试验数据吻合性较好,岩石试样的单轴压缩试验结果如图5。图6 展示了数值模拟离散裂隙网络(DFN)随时间变化分布情况。获得的应力应变曲线见图7。

表3 线性模型力学参数Table 3 Mechanical parameters of the linear model

表4 线性平行粘结模型细观力学参数Table 4 Micro mechanical parameters of the linear parallel bond model

表5 光滑节理模型细观力学参数Table 5 Micro mechanical parameters of the smooth joint model

图5 室内单轴抗压实验试样Fig.5 Uniaxial compression test specimen

图6 离散裂隙网络(DFN)分布Fig.6 Distribution of discrete fracture network (DFN)
2 滚刀模型建立
为了对滚刀破岩过程分析,建立了尺寸为300 mm×150 mm 的非均质花岗岩颗粒流模型,模型共包含13768 个颗粒,3584 个颗粒簇,其中颗粒最小半径0.9 mm,最大粒径与最小粒径比为1.22,粒径值由高斯函数随机指定。考虑实际运用中滚刀刀圈强度-刚度相对于岩石材料均处于较高水平,故采用刚性圆形墙体表征滚刀,墙体直径432 mm,滚刀模型如图8 所示。学者研究表明,法向推力在滚刀破岩过程中起主要作用,整个过程可简化成滚刀侵入岩体过程[25-26]。模型设定滚刀滚动速度5 mm/s,贯入度3 mm,竖直方向施加的超声波振动载荷频率为20 kHz,振幅为20 μm。

图7 应力应变曲线Fig.7 Stress vs strain curve

图8 滚刀滚动碎岩模型Fig.8 Rock breaking model of the rolling disc cutter
3 裂纹萌生与损伤演化
离散元模拟结果中可通过接触力链、离散裂隙网格等的分布特性表征模拟过程中细观力学特性及破坏发展情况。
3.1 接触力链分布特征
颗粒流模型中介质应力是以一种特殊的方式进行表达的。迭代运算中,在牛顿运动定律获得颗粒位移的基础上,颗粒与颗粒、颗粒与墙体间接触点的力和力矩通过力-位移定律计算得知,此刻模型中每个接触点力的性质与大小都是可获得的,所有接触点的力勾连组合形成模型整体的力链分布,做到通过微观接触力实现宏观应力传递的表征。
图9 展示的是在模型稳定运行后,一个周期的超声波振动下,滚刀滚动加载过程中花岗岩模型内部接触力链的变化情况,其中绿色区域表示拉应力链,蓝色区域表示压应力链。图9(a)~(e)分别展示的是模型在加载一个周期内,0、T/4、T/2、3T/4、T时刻的接触力链分布特征,其中T表示超声波振动周期。T/4、3T/4 时刻分别对应该振动周期内,滚刀所处位置的最低点与最高点。
可明显看出,岩石模型颗粒的接触力类型在一个振动周期呈现拉应力与压应力的交替变换,呈现绿色的拉应力由岩石模型上表面中心受力点处向岩石内部传播,拉应力分布呈现圆环状,具有明显的波的传播特征。T/4 时刻,滚刀在超声波加载的最低点处,力的作用点处呈现压应力,以该点为中心的一定大小的扇形区域内呈现拉应力,其中以上表面附近的两个30°角区域拉应力分布最为密集(图9b)。随后压应力区面积增大,伴随拉应力区向两侧及深部扩散(图9c)。3T/4 时刻,岩石内部一定深度处形成一个环形拉应力带(图9d)。
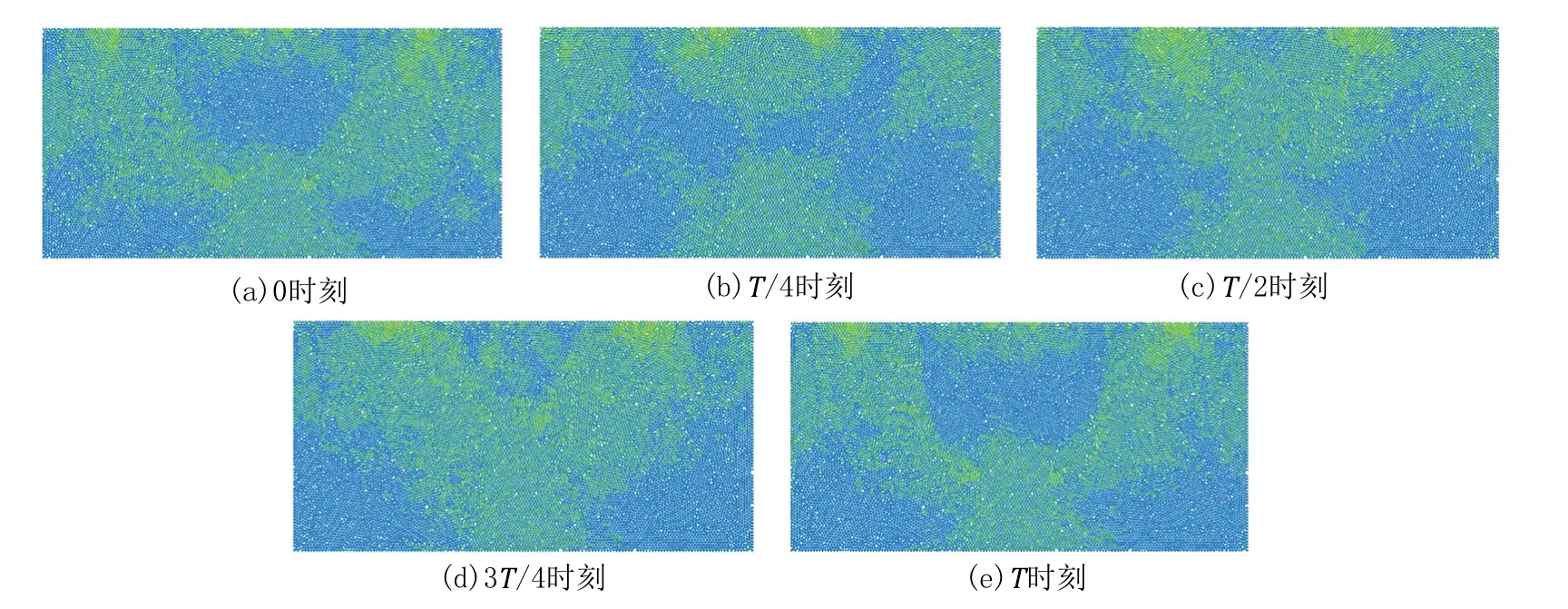
图9 岩石内接触力链位置分布Fig.9 Distribution of the contact force chain in rock
图10(a)~(e)分别展示了加载一个周期内,0、T/4、T/2、3T/4、T 时刻岩石内应力链强弱分布特征。应力的扩展传播呈现较为明显的扇形,压应力扇形区角度约为120°,中心点对称两侧30°角范围内,拉应力起主导作用(图10b)。由图10(c)可看出,压应力区中,同半径位置点,平行于加载方向处的应力值最大,应力值随与加载方向的夹角增大而逐渐减小。由图10(d)、(e)可看出,在一次新的向下运动过程中,一个新的扇形压应力区生成,上一个压应力波呈环形带状位于一定深度处,两压力波中间夹杂着一条环形拉应力波。
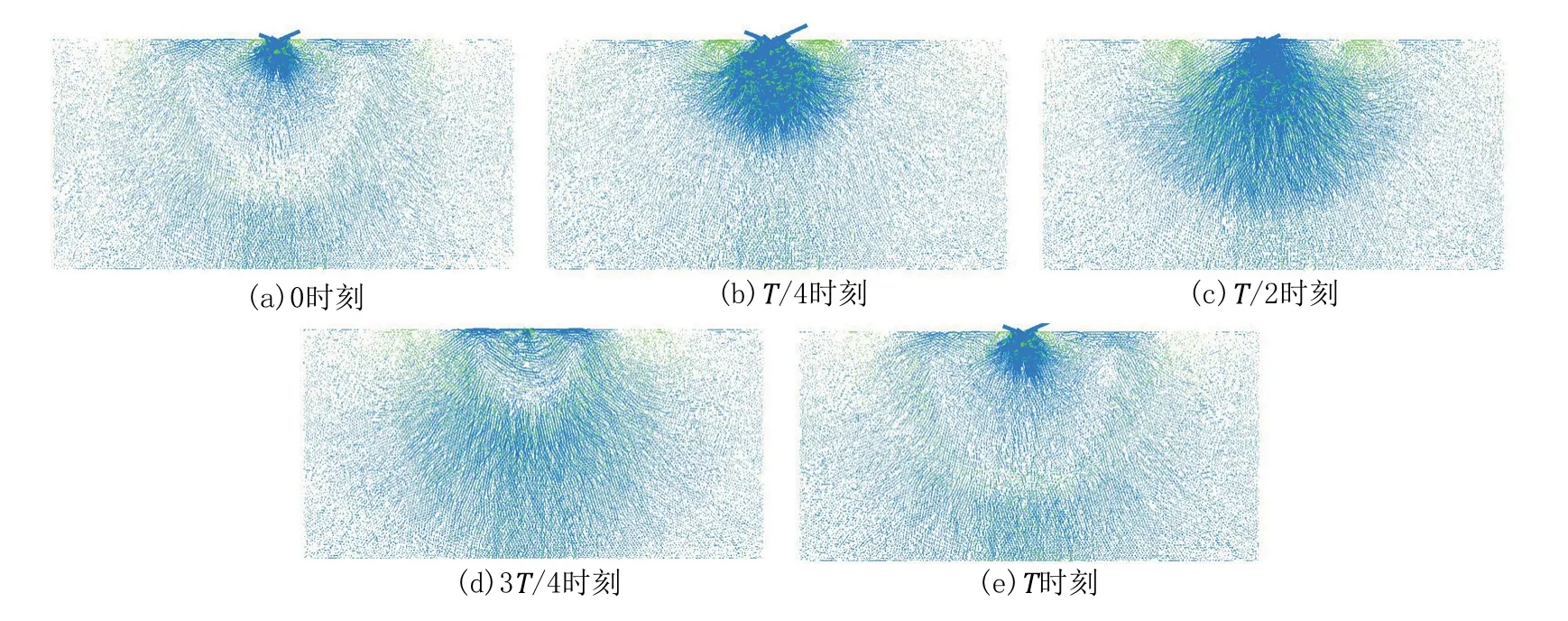
图10 岩石内部应力链强弱分布Fig.10 Strength distribution of the stress chain in rock
3.2 模型内部裂纹时空演化特征
图11 展示的是相同加载周期下,超声波振动辅助作用与原生无辅助作用下,岩石内部裂纹随加载时间变化曲线。超声辅助加载模式下,各类裂纹的产生规模均大于传统纯滚动加载模式,其中裂纹总数目提升30.3%,且超声波振动加载提前了岩石内部裂纹生成的时间,提升效果达到56.3%。传统模式加载过程中,岩石内部出现了多次裂纹激增现象,即跃进式破岩现象,而超声波振动加载辅助作用模式下,裂纹的生成较为平缓,仅出现一次激增现象。拉伸裂纹决定了材料脆性破坏特征,剪切裂纹决定材料延-塑性特征,两种加载模式下,拉伸破坏裂纹的数目占比达到66.8%,均多于剪切破坏裂纹,拉伸破坏是滚刀碎岩过程中岩石内部的主要开裂形式[27]。
离散裂隙网络是岩体数值模拟中常用的裂隙构建及测量的途径[27-28]。图12(a)、(b)分别展示了纯滚动状态下与超声波振动辅助加载状态下离散裂隙网络随加载时间演化分布情况。两种加载状态下,裂隙均随加载时间的增加呈现由浅至深、从中间到四周扩散的生成趋势。可以发现,常规加载模式下裂隙生成起始区域位于距上表面一定深度处,超声波振动辅助加载在岩石表层会生成更多的裂隙,且在加载初期,裂隙的生成量显著多于常规模式。两种模式下均在相同缺陷位置处生成了裂隙带,超声波振动辅助加载生成的裂隙带宽度更大,生成时间相对提前。
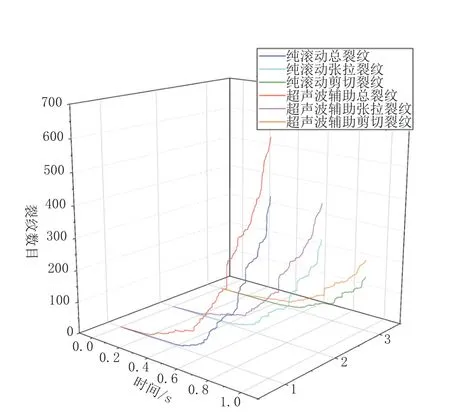
图11 裂纹数目随时间变化曲线Fig.11 Curve of crack number vs time

图12 离散裂隙网络随时间变化分布Fig.12 Distribution of discrete fracture network vs time
3.3 模型内部裂纹方位角演化特征
对计算过程等间距选取10 个采样点,统计了纯滚动与超声波振动辅助两种加载状态下,花岗岩内部裂纹方位角的动态演化趋势,如图13、图14 所示,(a)~(j)分别展示了10 个采样点的各方位角下裂纹的统计情况。外围圆周坐标数值0~360 表示裂纹的方位角,内部圆形等值线代表裂纹的强度,玫瑰图的花瓣长度表征了特定方位下裂纹出现的频率。
图中90°方向为超声波加载方向,135°为滚刀滚动方向。由图13 可知,纯滚动加载模式下,第1 个采样点无裂纹生成,自第2 采样点开始,在滚刀滚动方向前侧产生裂纹,第5 采样点时是裂纹的大范围萌生期,在70°、90°、100°、140°方向上均有较多裂纹生成,第6 采样点起,裂纹主要沿100°方向萌生扩展。由图14 可发现,第1 采样点即检测到裂纹的萌生,可知超声波辅助加载加速了裂纹的生成,随后在2、3 采样点,裂纹的大范围萌生期出现,20°~140°均有较多裂纹生成,相对于纯滚动加载模式裂纹生成方位角范围更宽,1~5 检测点可以发现,90°是裂纹的主要生成方位角,该方向也是超声波振动加载方向,从第6 采样点起,100°方向裂纹生成数量逐步成为裂纹生成主导方向。对比可知,在整个加载周期过程中,超声波振动在前期主导了裂纹的生成,随着加载的进行,滚动载荷作用回归主导地位。相比于纯滚动加载模式,超声波振动加载模式辅助促进了裂纹的生成。
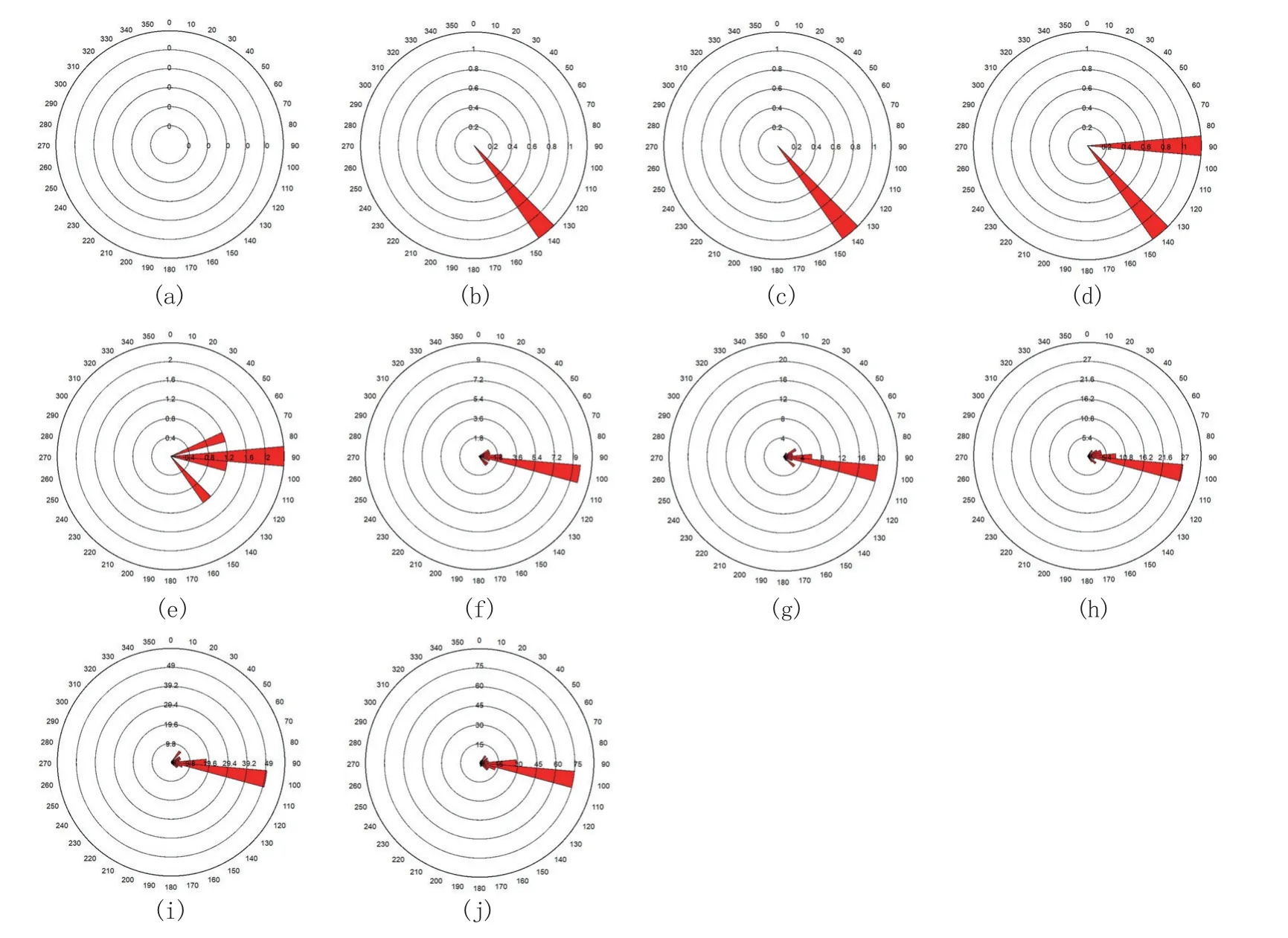
图13 滚刀纯滚动下岩石裂纹方位角演化特征Fig.13 Evolution characteristics of the rock crack azimuth with pure rolling of the disc cutter

图14 超声波振动滚刀岩石裂纹方位角演化特征Fig.14 Evolution characteristics of the rock crack azimuth with the ultrasonic vibration-assisted disc cutter
4 结论
本文提出了一种新的滚刀碎岩方式,将超声波振动加载与滚刀滚动加载耦合作用,优化滚刀破岩性能,增益破岩效果。通过离散单元法对纯滚动与超声波振动辅助加载模式下滚刀破岩过程进行了模拟对比,得出以下结论:
(1)滚刀在超声波振动加载辅助下能够以岩-机作用点为中心周期性地产生拉、压应力波,并向岩石内部传播。在岩石的近表面滚刀作用点周边区域周期性地产生较为强烈的拉应力,对岩石浅层近表面部位的张拉破坏有较为明显的促进作用。
(2)超声波振动提升了滚刀滚动作用下裂纹生成的规模,且加快了裂纹的生成速度,大幅提前了裂纹初次萌生时间,使滚刀在加载初期即在岩石浅层部位作用生成微裂纹。
(3)超声波振动辅助加载模式下岩石内部裂纹生成更加平稳,跃进式破碎现象较少,能够有效避免因剧烈振动产生的冲击载荷对滚刀刀圈产生异常磨损和非常规结构破坏,对延长滚刀寿命具有促进作用。
