基于安时积分法和UKF的锂电池SOC估测

刘迪，李琳，姜晓健

（西安石油大学 电子工程学院，陕西 西安 710065）

0 引言

当今社会能源短缺，为兼顾环保与节能两个方面，电动汽车出现在人们的视野当中。电动汽车领域取得了快速的发展，其中最重要的就是汽车的锂电池，准确地估测出锂电池各种状态是目前研究的重中之重。电池管理系统（Battery Management System, BMS）是电动汽车最重要的一部分，BMS最重要的指标是能够准确地估测锂电池的SOC值。准确的SOC值能够提高锂电池重复利用效率、增加锂电池使用寿命[1]。同时，想要深入地研究电池的特性，需要对锂电池进行建模，锂电池模型是对锂电池的等效转化，精确的锂电池模型能够完美地表达出电池的动静态特性，也是提高SOC估测精度的基础。本文采用二阶RC电路模型，结合安时积分法与UKF算法，在matlab上搭建仿真模型，将搭建的EKF与AH-UKF算法模型通过脉冲放电实验所获得的数据进行比对。结果表明，EKF算法平均相对误差为1.96%，AH-UKF算法平均相对误差为0.95%，因此AH-UKF算法能更好地减小误差，可实际应用。

1 锂电池模型建立

现阶段锂电池等效模型主要分为三大类：电化学模型、等效电路模型、人工神经网络模型。电化学模型：最能表征电池特性，但电化学模型内部结构复杂、计算繁琐、在建立模型期间耗费时间，因此大多不采用。人工神经网络模型：具有自学习能力，可以高速寻找优化解的能力，但需要大量的数据源作为参考对象，依赖于数据量大小。等效电路模型：用电压源、电阻、电容组成的等效电路模型来表征电池的内部特性。相对于其他两种模型，等效电路模型计算量相对较小且精度高，在锂电池研究领域应用广泛。本文采用等效电路模型来模拟电池内部特性。常见的等效电路模型[2]分为Rint模型、二阶RC模型、Thevenin模型、PNGV模型，还有多阶RC模型。表1为各种等效模型特点：

表1 各种锂电池模型特点

综合多种模型优缺点，本文选择二阶RC等效模型对锂电池进行建模。图1为二阶RC等效电路模型：

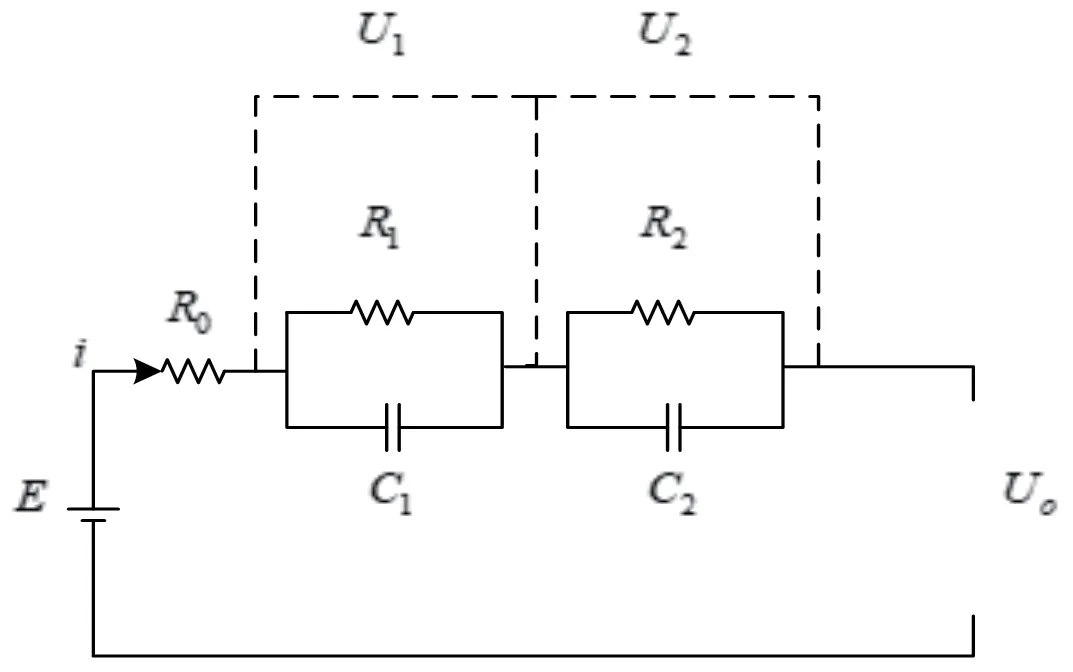
图1 二阶RC等效电路模型

图中：E为电池的电动势，R0表示电池欧姆内阻产生的极化，R1和R2为电池的极化电阻，分别表示电池的电化学极化和浓差极化，C1和C2为对应的极化电容，i为流过负载电流，规定图中电流为正；该模型能够精确地反映出电池静态、动态特性，没有较大计算量，是目前锂电池估测精度最优的模型。

根据所建立的模型，可以列出相应的函数表达式：

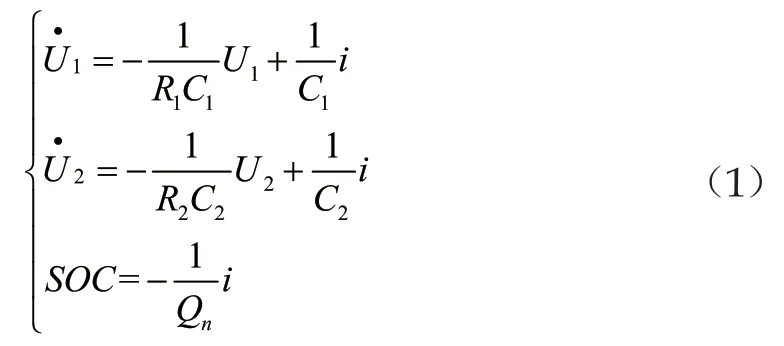
输出方程为：

2 锂电池参数辨识

实验使用的电池型号为三星INR18650-30Q。标称容量为：3000 mAh，充电电压：4.2 V，标称电压：3.7 V。使用电池充放电仪对锂电池进行充放电实验，具体实验步骤如下：采用标准充电实验将电池充满电量，将其静置2 h纪录电压值并标定所对应的SOC值为1；将电池充放仪放电电流设置为3 A，并设置合理的采样时间；开启电池充放仪，使电池放电，设置放电时间为3 min，放电结束后将电池静置10 min，纪录此时电压并纪录电压所对应的SOC值为0.95；重复实验步骤（3），直至电池不再放电，记录其SOC值为0；进行多次实验，选取合适的实验数据作为电池放电数据。

表2为锂电池从满电状态到空电状态的电池电动势与SOC值对应数值（E-SOC），E-SOC对应数值如表2所示：

表2 E-SOC对应值

将数据带入到Matlab中进行曲线拟合，得到E-SOC曲线拟合图，如图2所示；

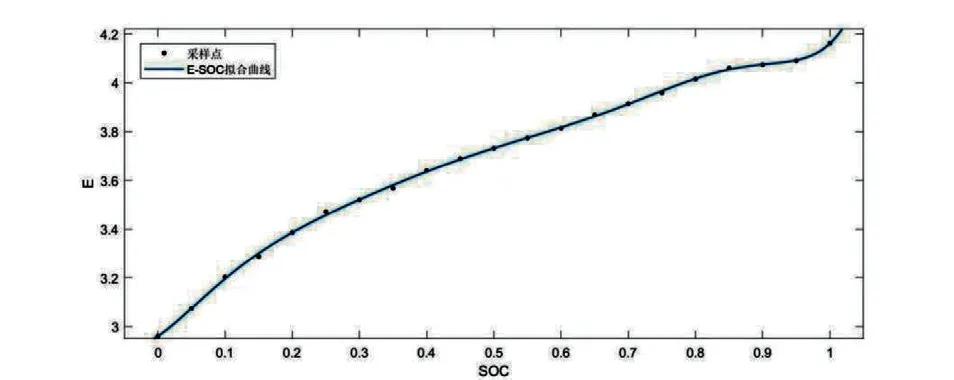
图2 E-SOC辨识曲线

并且使用拟合后的曲线作为E-SOC辨识结果，辨识得到的函数如下：

通过测得的电池端电压、电流以及E-SOC拟合曲线使用最小二乘法进行参数辨识，得到R0、R1、R2、C1、C2。将辨识参数带入到模型当中，验证模型准确性，具体步骤如下：

首先对锂电池进行标准充电，此时SOC值为1。采用脉冲放电试验对锂电池进行放电，使用电池放电仪对锂电池进行放电，记录电池端电压以及电流，将记录下来的数据导入到Matlab中，得到模型输出电压如图3所示，将两者进行比较得到模型误差如图4所示。

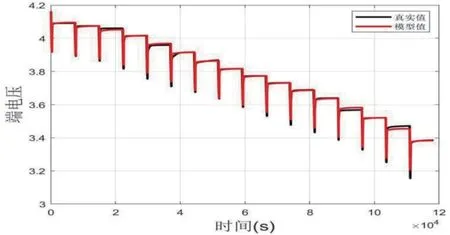
图3 锂电池端电压与模型输出电压比较值

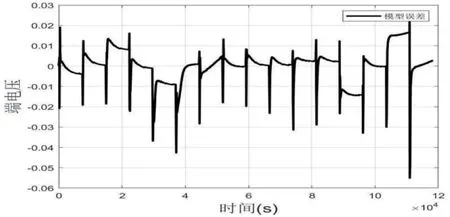
图4 模型误差

实验结果表明，建立的电池等效模型可以准确地描述电池的内部特性，实验误差小，平均误差5.1 mV，可以用来等效实际的锂电池。

3 基于安时积分法（AH）和无迹卡尔曼（UKF）UKF的锂电池SOC估测

常用的估算锂电池SOC值的方法[3]有安时积分法、开路电压法、卡尔曼滤波算法、人工神经网络算法以及结合算法等。

（1）安时积分法：通过已知上一刻锂电池的电量，同时对电池中电流在放电期间进行积分，将两者求差，即可得出当前时刻电池SOC值，具体公式如下：

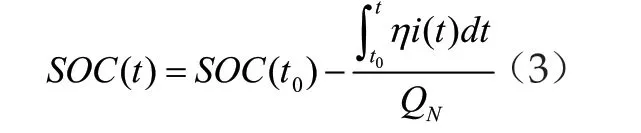
该算法受到电池初始SOC影响，当锂电池初始SOC值不准时，由于迭代积累计算，算法收敛性会越来越差，因此需要精准的初始值来作为基础。

（2）开路电压法：锂电池的SOC值与锂电池电动势在数值上十分相近，可以反复进行实验对锂电池进行充放电测试建立锂电池OCV-SOC对应表格，可以根据表格一一查找对应关系。

（3）人工神经网络算法：非线性拟合能力强，需使用大量实验数据进行训练且在学习过程中收敛较为缓慢。

（4）卡尔曼滤波算法[4]：根据所建立的锂电池模型建立状态方程以及观测方程，将方程离散化，通过上一时刻的SOC值来预测下一步的SOC值，由第一时刻不断进行更新，最终得到每一个阶段锂电池SOC的最优估计值。在线性系统中，卡尔曼滤波算法收敛性较强，得到的结果较准确，但对于锂电池这样的非线性系统，经常采用各种改进的卡尔曼滤波算法；本文采取无迹卡尔曼与安时积分法相结合的算法对锂电池SOC进行估测。

无迹卡尔曼滤波算法[5]（UKF）实现步骤如下：

（1）计算2n+1个Sigma点，即采样点。

（2）计算这些采样点相应的权值

（3）获得一组采样点以及对应权值。

（4）计算2n+1个Sigma点集的一步预测，i=1，2，……，2n+1。

（5）计算系统状态量的一步预测及协方差矩阵。

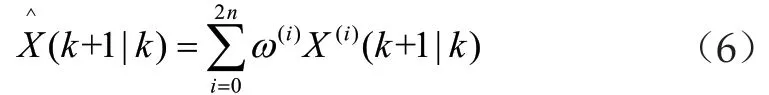
式中，Q为噪声协方差矩阵。

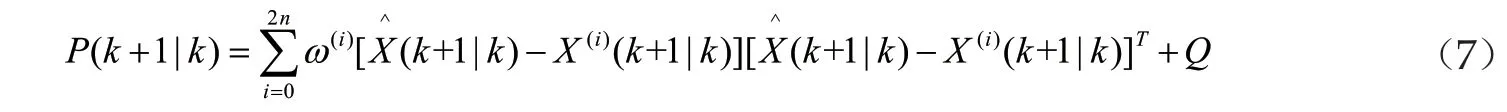
（6）进行一步预测值，再次使用UT变换，产生新 的Sigma点集。

（7）将上一步预测的Sigma点集带入观测方程，得到预测的观测量，i=1，2，……，2n+1。

（8）由上一步得到Sigma点集的观测预测值，通过加权求和得到系统预测的均值及协方差

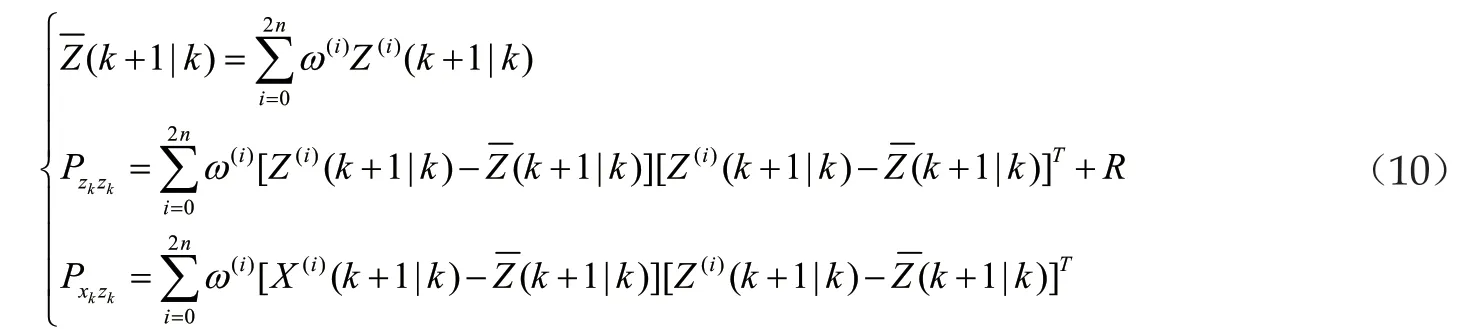
式中，R为观测噪声协方差矩阵。

（9）计算卡尔曼增益。

（10）计算系统状态更新和协方差更新。

无迹卡尔曼滤波在处理非线性滤波时并不需要在估计点处做泰勒级数展开，在进行前n阶近似，而是在估计点附近进行UT变换，是获得的Sigma点集的均值与协方差与原统计特性匹配，用来估算非线性形式的电池模型可以减少误差，提高精度。

4 仿真与结果分析

本文在MATLAB/Simulink中搭建仿真平台，搭建EKF[6]与UKF两种算法的锂电池SOC估测仿真模型，将两种模型进行对比，验证精度。

利用脉冲放电实验，对UKF于EKF算法初值进行设置：

上式中，Q为系统误差协方差，P为状态误差协方差初始值。

EKF仿真结果：

由图5分析可知：使用EKF算法估算[7-8]，在初期，由于电池内部特性，其电化学反应未稳定，采用非线性卡尔曼滤波算法误差较大。随着锂电池放电，锂电池放电曲线趋于平稳，算法估测曲线与实际放电曲线收敛性较好。由EKF算法估测锂电池SOC值的平均相对误差为1.96%，能较好地较小估算误差。

图5 EKF仿真与实际SOC值对比

AH-UKF[9]仿真结果：

由图6分析可知：在仿真初始阶段（100%-85%），由于初值较为准确，因此采用安时积分法，安时积分法初值即为电池采用标准充电充满时的SOC值，该值较为准确，误差几乎可以忽略，可以近似相当于一条直线；仿真中期，随着锂电池放电的进行，电池放电平台趋于稳定，因此使用安时积分法时，初值的变化范围不大，所以算法估算误差较大，因此采用无迹卡尔曼滤波算法，AHUKF算法平均相对误差为0.95%。该实验结果表明，AHUKF算法精确度高，可以更好地减小估测误差。

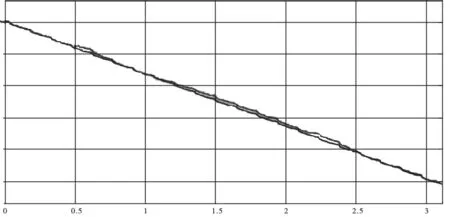
图6 AH-UKF仿真与实际SOC对比

5 结语

本文通过建立二阶RC等效电路模型，采用脉冲放电实验对锂电池进行参数辨识，将辨识得到的参数带入到建立模型中，验证了模型准确性。在MATLAB/Simulink中搭建仿真平台，将EKF算法与AH-UKF算法比对，结果证明AH-UKF算法准确度更高，误差更小。能够更好地用来估测SOC值。