一种升降机的粒子群优化模糊 PID参数的控制器设计

张韶宇，杨山坡，史文祥，娄燕鹏，李 欢

1中国船舶重工集团公司第七二五研究所 河南洛阳 471023

2成都西部泰力智能设备股份有限公司 四川成都 610031

在 工业生产中，升降机常用于人或物的垂直运输。某电厂需要一台升降机，将生产所需的原料组件从厂房操作平台送至下方水池底部附近 (行程8 m)，然后由原料组件抓取机进行水下操作。在运输过程中，原料组件对速度和振动均有严格的要求，因而升降小车的速度控制要平稳。该升降机的工作原理与提升机类似，由钢丝绳牵引小车沿轨道移动。如果采用传统的 PID 控制升降小车，会出现因小车速度的时变、非线性、纯滞后等问题而引起振动[1-2]，损伤原料组件，并加速升降机机械部件的老化。

为了精准控制升降速度，降低小车的振动，笔者采用粒子群优化算法 (Particle Swarm Optimization，PSO) 对模糊 PID 控制器中的量化因子和比例因子等参数进行优化[3]，实现自动调整和完善运行速度的目标，并进行了现场验证。

1 设备方案

该升降机由机械和电气两部分组成，如图 1 所示。机械部分主要由减速器、卷筒、轨道和升降小车等组成。电气部分主要由触摸屏、S7-1500 PLC、控制按钮、变频器、编码器和称重传感器等组成。

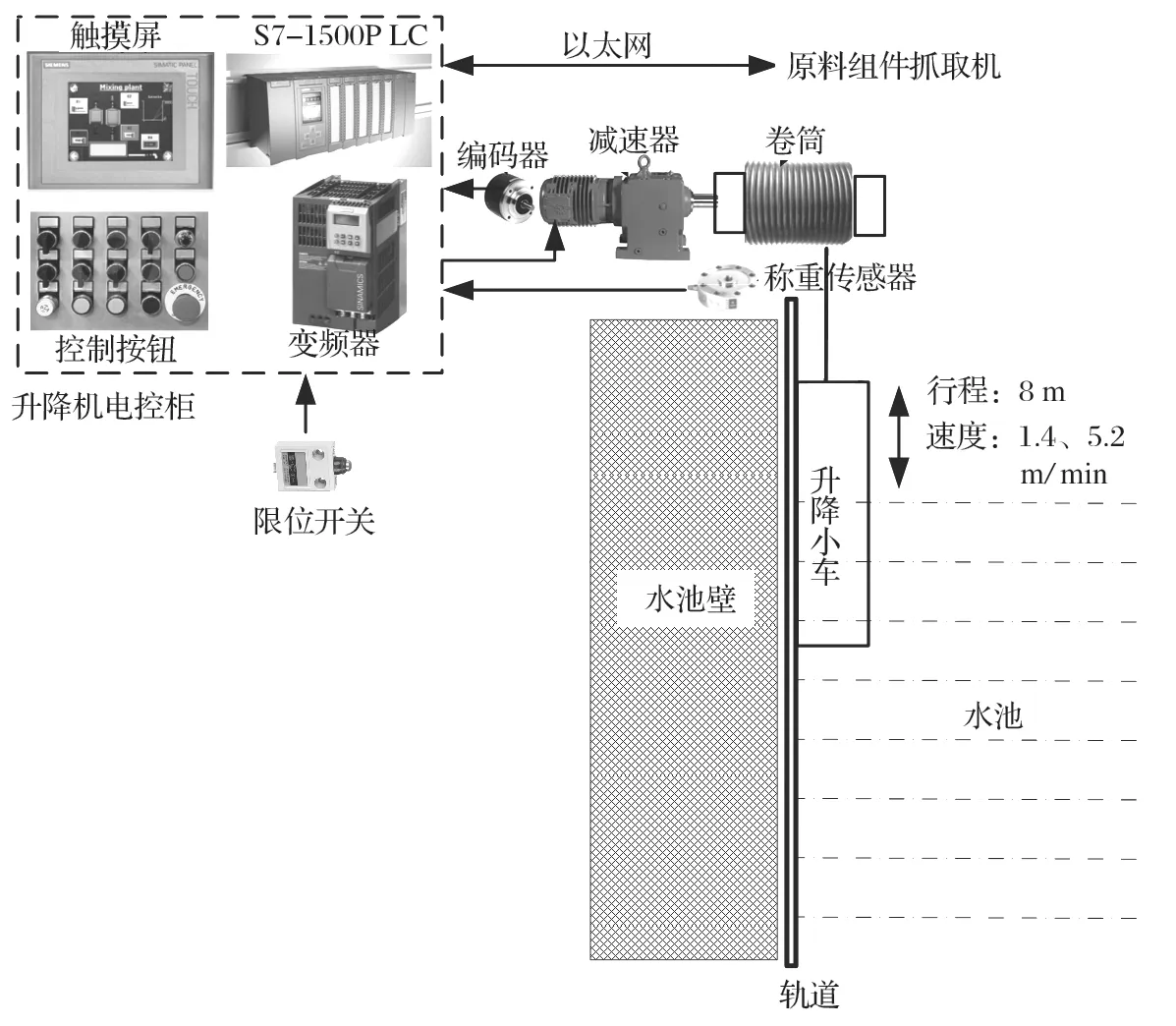
图1 原料组件升降机系统组成Fig.1 Constitution of raw material and component elevator system

在触摸屏中设定小车的升降速度，PLC 的模糊PID 控制器输出指令传到变频器，由变频器控制减速器带动卷筒转动，由钢丝绳牵引小车沿轨道上下移动。编码器与 PLC 相连，可检测减速器的转速，通过机械传动比可计算得到小车的移动速度，当前速度与设定速度的差值和变化率被传送到模糊 PID 控制器，模糊 PID 的输出再通过变频器、减速器、卷筒等控制小车的速度，从而实现小车速度的闭环控制。

由于模糊 PID 的控制参数需要根据大量的试验结果并通过一定优化方法才能获得[4-6]，所以笔者采用 PSO 算法方法来优化模糊 PID 控制器的参数。通过“PLC 控制+变频驱动+速度反馈系统”的控制结构，有效改善升降小车运行的平稳性，降低超调量，减少调节时间，提高响应速度和抗干扰能力，从而精确控制升降小车运动，减小其振动。

2 PSO 优化模糊 PID 参数的控制器设计

基于 PSO 算法优化方法而设计的升降机模糊自适应 PID 速度控制器原理如图 2 所示。编码器实时获取升降小车的速度，由设定速度和当前速度可获得速度的偏差e，由当前偏差和上次偏差可获得偏差的变化ec。模糊控制器首先对e和ec进行模糊化计算，再由模糊控制规则作出相应的逻辑推理和判断，获得 PID 控制器的调整参数；然后根据PID 控制参数的初始值，得到新的 PID 控制参数Kp、Ki和Kd；最后再经过 PID 控制器产生新的输出量来控制被控对象。

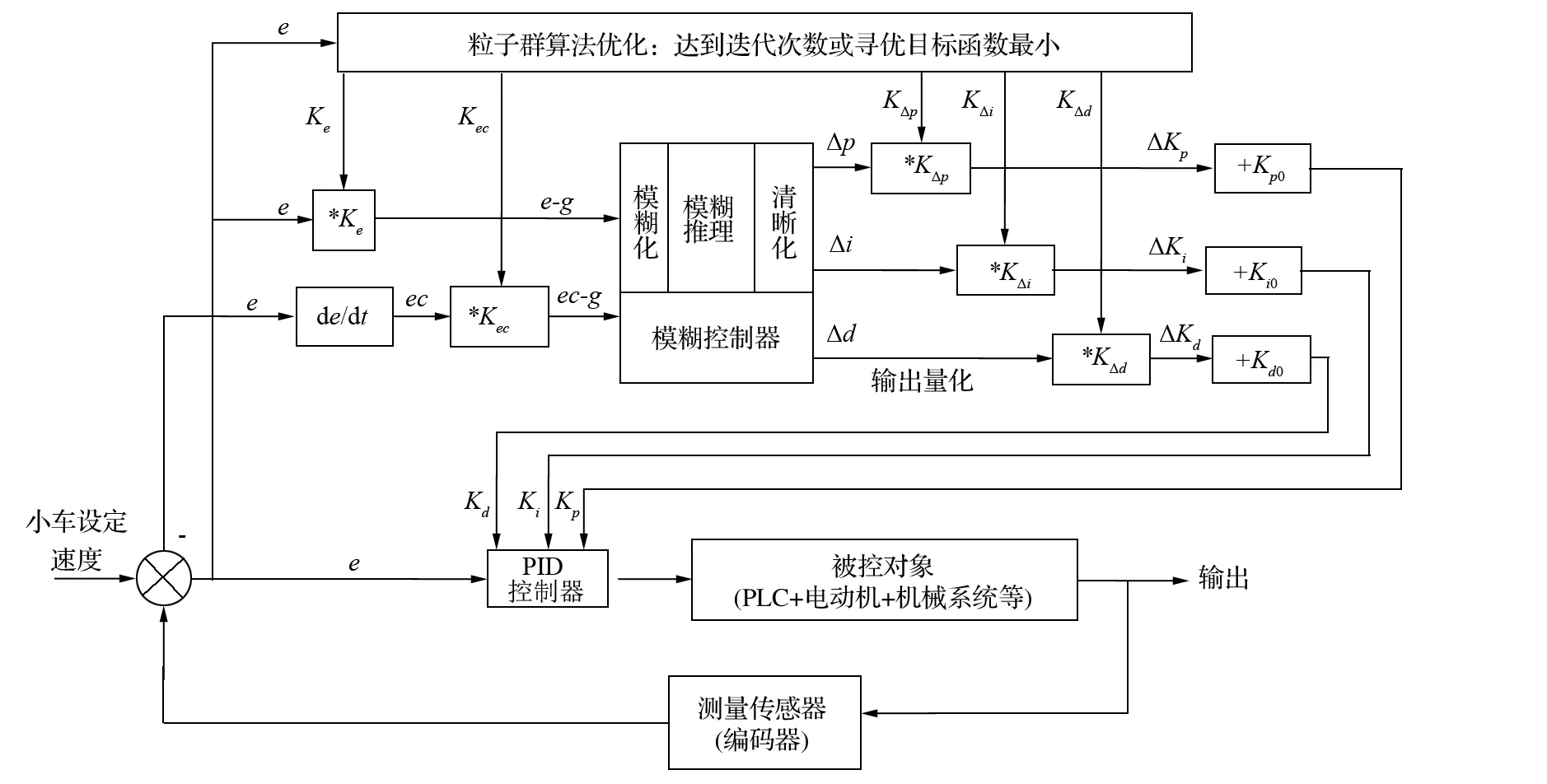
图2 基于 PSO 算法优化的模糊自适应 PID 速度控制器原理Fig.2 Principle of fuzzy self-adaptive PID speed controller based on PSO algorithm

模糊控制器的输入变量和输出变量都具有固定的量化论域，输入变量e和ec分别乘以相应的输入量化因子Ke和Kec后，得到输入量化变量e-g和ec-g，其值的变化范围对应输入量化论域。同理，输出变量Δp、Δi和Δd分别乘以相应的输出比例因子KΔp、KΔi和KΔd后，得到输出量化变量ΔKp、ΔKi和ΔKd，其值的变化范围对应输出量化论域。模糊控制器的输入量化因子和输出比例因子需要采用 PSO 算法进行优化选择。

2.1 模糊控制器设计

模糊控制器主要由 3 个模块组成：模糊化模块、模糊推理模块和清晰化模块[7]。

2.1.1 模糊化模块

模糊化模块主要将数字形式的输入转化为模糊语言标识的值，根据建立的输入隶属度函数，将输入的精确量转换为模糊量，然后将模糊量映射到相应的模糊控制论域中，这就是模糊化过程。通过模糊化过程将不同输入量的精确值转换成不同的模糊变量值，最终形成一个模糊集合。

语言变量及隶属函数将误差 (e-g) 及误差的变化率 (ec-g) 根据其变化特点，在映射的模糊论域中建立 7 个模糊语言变量 (负大、负中、负小、零、正小、正中和正大)，分别用 NB，NM，NS，ZO，PS，PM，PB 表示，输入变量e-g和ec-g量化论域为[-6，6]。输出语言增量为Δp、Δi和Δd，语言变量值取{NB，NM，NS，0，PS，PM，PB} 7 个模糊值，输出变量Δp、Δi和Δd的量化论域均定为 [-10，10]。输入变量隶属度函数和输出变量隶属度函数分别如图 3、4 所示。

2.1.2 模糊推理模块

选择 Mamdani 型模糊控制规则，根据e-g和ec-g的 7 个模糊变量，共输出 49 条控制规则，建立Δp、Δi和Δd的模糊规则如表 1 所列。根据输入到模糊控制器的e-g和ec-g，可得到它们各所对应的隶属度，然后根据表 1 找出输出值Δp、Δi和Δd所对应的隶属度。

2.1.3 清晰化模块

笔者采用的解模糊方法为重心法，其表达式为

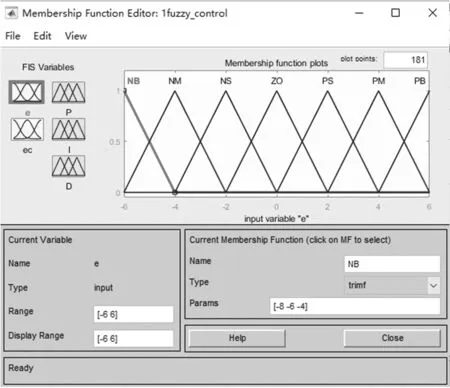
图3 输入变量隶属度函数Fig.3 Membership function of input parameters

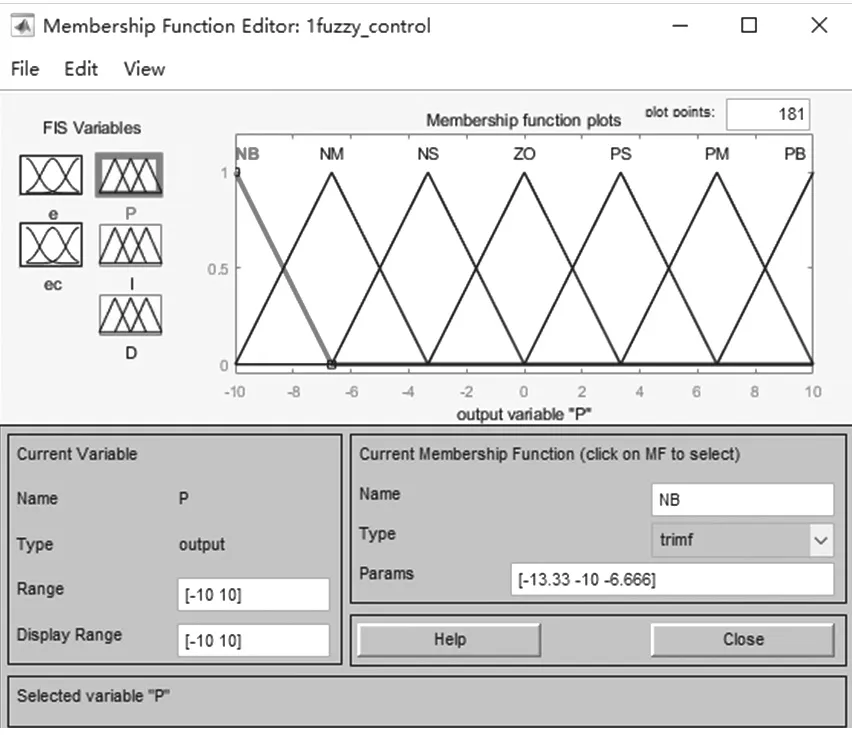
图4 输出变量隶属度函数Fig.4 Membership function of output parameters

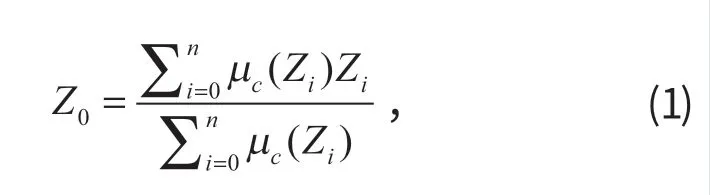
式中：Z0为模糊控制器的输出变量经过解模糊后的精确值；Zi为模糊控制量在论域内的量化值；μ c(Zi) 为Zi的隶属度值。

经过清晰化后可分别求得Δp、Δi和Δd的精确值。

在模糊 PID 控制器中，PID 的调整参数为

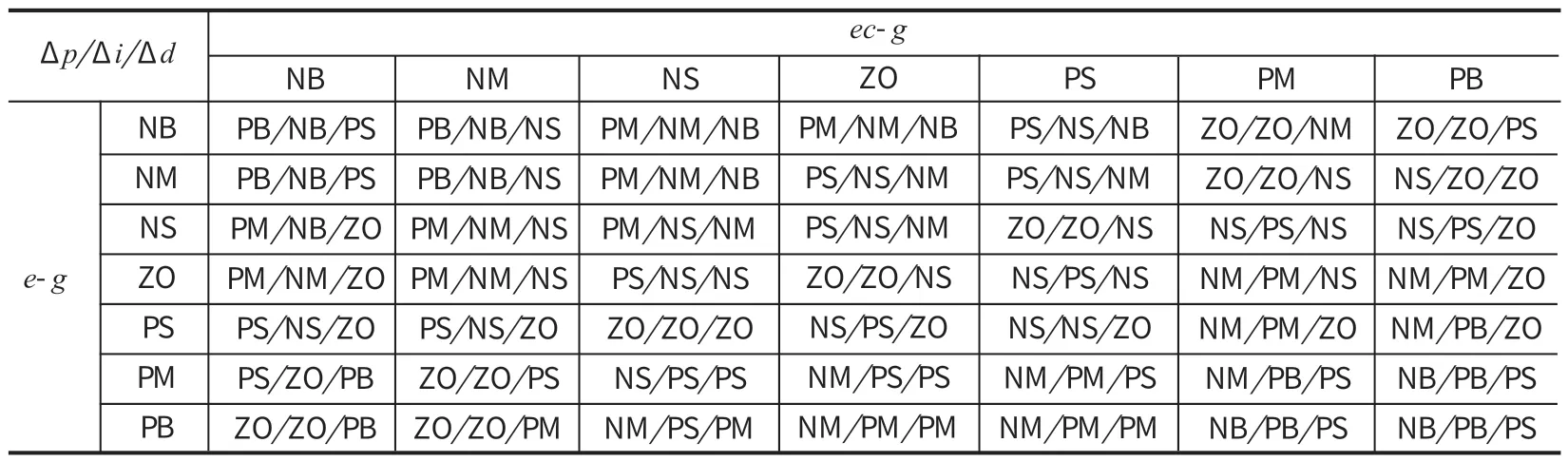
表1 Δp、Δi 和Δd 的模糊规则Tab.1 Fuzzy rules of Δp,Δi andΔd

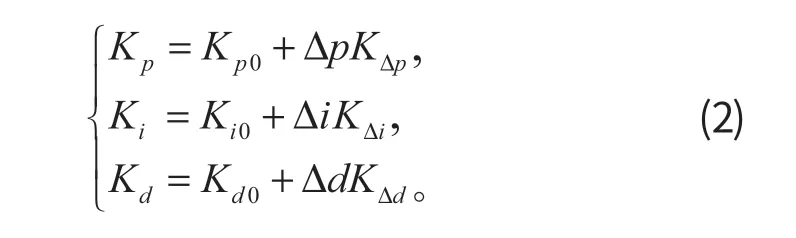
式中：Kp、Ki、Kd分别为 PID 控制器的参数；Kp0、Ki0、Kd0为对应的初始参数，通过常规方法可得。

在线运行过程中，将e-g和ec-g，Δp、Δi和Δd所对应的 PID 参数模糊调整矩阵表存入程序储存器中供查询[8]。控制系统根据检测系统的输出值，与设定值比较后实时计算偏差e和偏差变化率ec，经模糊化后查询模糊调整矩阵表，通过清晰化后可得到调整量Δp、Δi和Δd，将各个调整量分别带入式 (2)、(3)、(4) 后，可得到 PID 控制器的各控制参数Kp、Ki、Kd，用于 PID 控制的输出。

2.2 模糊 PID 控制在 PLC 中的实现

针对西门子 S7-1500 PLC，笔者采用 STEP7 编程软件和模块化设计方法进行编程。在程序块中，OB1 为主程序块；OB30 为中断程序，主要完成模拟量输入/输出操作和 PID 控制等程序；FB17 是具有模糊 PID 控制功能的程序块，如图 5 所示，在OB30 中被调用。在 FB17 程序块的 DB 数据模块中的OUTPUT，建立一个“fuzzy control”模糊控制表，如图 6 所示，可实现表 1 的模糊推理功能，根据输入e-g和ec-g的值，选择出输出值Δp、Δi和Δd所对应的隶属度。图 7 所示为计算e和ec的程序。

2.3 基于 PSO 的模糊 PID 控制器的参数寻优

在模糊 PID 控制器中，输入量化因子Ke和Kec，输出比例因子KΔp、KΔi和KΔd的值直接影响其控制效果。通常情况下，模糊 PID 控制器想要获得理想的动态特性，需要通过大量现场试验，然后利用人工经验选择合适的量化因子和比例因子，但这种方法可能无法获得最佳值。

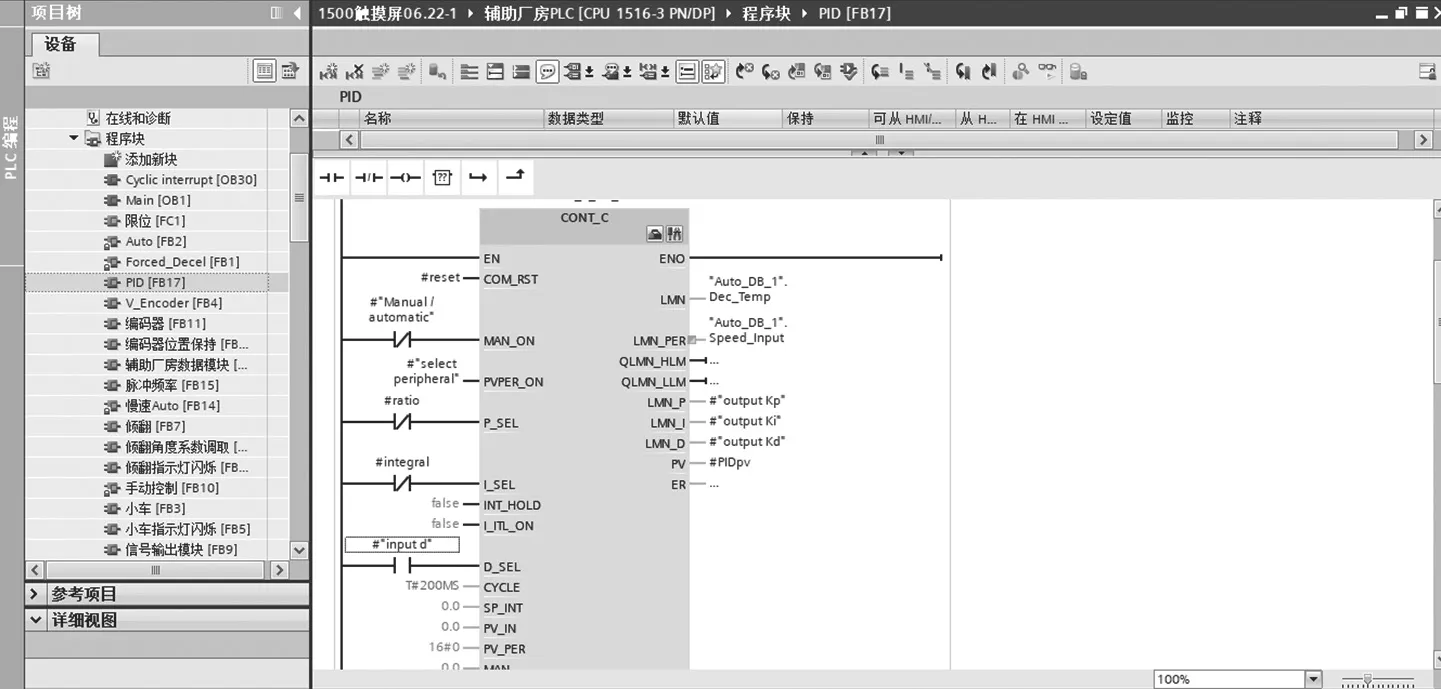
图5 PID 控制程序Fig.5 Control program of PID

图6 模糊控制表Fig.6 Fuzzy control table

图7 计算 e 和 ec 的程序Fig.7 Program of e and ec calculation

基于鸟群觅食行为而研究得出的 PSO 优化算法是通过群体中个体之间的协作和信息共享来寻找最优解，特别适合模糊控制系统中的参数优化。为了确保对小车升降速度的精确控制，利用PSO 算法对模糊 PID 控制的量化因子和比例因子进行优化[9]。

在 PSO 算法中，每个粒子都有当前的速度和位置信息，可计算出每个粒子所对应的最优值和全局最优解，然后将这些信息作为经验进行动态调整。优化算法结束的条件是迭代次数达到设定值，或寻优目标函数达到最小。针对模糊 PID 控制器的参数寻优，本次 PSO 算法中选择的目标函数为

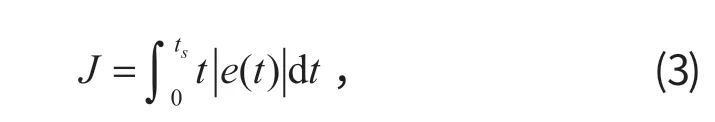
式中：ts为试验时间；e(t) 为t时刻设定值与当前值的误差。

采用 ITAE 准则进行优化，优化时对系统初始误差考虑较少，主要是限制过渡过程后期出现的误差。优化后的系统一般具有快速、平稳、超调量小的特点。

PSO 优化流程如图 8 所示。优化时选择参数如下：粒子种群数量为 500，粒子的维数为 5，量化因子Ke和Kec及比例因子KΔp、KΔi和KΔd的初始值设定为 [2，2，2，2，2]，最大迭代次数为 200，粒子的速度范围为 [-1 000，1 000]，粒子的位置范围为[-8，8]。在现场进行联机试验时，将 PLC 中模糊 PID控制过程中的e和ec不断输入到上位机的 PSO 算法中，经过优化得到的参数为：Ke=4.9，Kec=5.4，KΔp=4.3，KΔi=7.52，KΔd=8。

图8 PSO 优化流程Fig.8 Optimization program of PSO

3 系统实际运用和分析

分别采用未优化参数的模糊 PID 控制方式和 PSO优化后的模糊 PID 控制方式进行升降小车的现场试验，通过博图软件监控实际调控过程中的速度变化，结果如图 9 所示。试验运行时间为 120 s，速度信号在前 60 s 由规定速度降为零，后 60 s 速度由零升至指定速度，输入控制方式中包含跳跃信号。由图 9 可以看出，经 PSO 优化的模糊 PID 控制器明显比未优化的模糊 PID 控制器响应更加快速，超调量小，没有明显的震荡，能有效提高控制系统的动态稳定性，减小振动。

4 结论

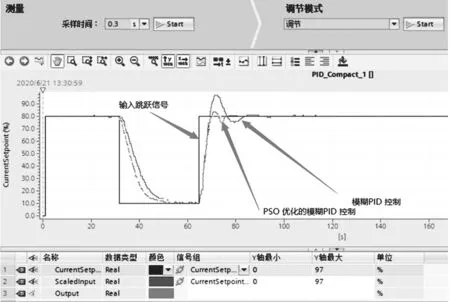
图9 监控界面上监控调速曲线Fig.9 Speed control curve on monitoring interface

由于升降机工作过程中，运行机构长期处于纠偏状态，会出现明显的震荡现象，必须提高控制系统的平稳性以及抗干扰能力。基于传统 PID 控制和常规模糊控制系统，提出一种基于 PSO 优化的模糊 PID 控制算法，对其系统的模糊 PID 控制器的参数进行优化。该算法一方面可以自行对参数进行优化控制，另一方面控制无需特定对象。研究结果表明，采用 PSO优化后，小车的速度调节具有超调量小、上升时间短、响应速度快、稳定性好、抗干扰能力强等优点，可增加钢丝绳的使用寿命，使控制更加平顺，降低机械结构的振动，减少对物料组件的伤害。