基于Thomeer函数的中东区块碳酸盐岩储层渗透率评价
2021-03-25张冲汤潇倪国辉闵云艺张亚男
张冲,汤潇,倪国辉,闵云艺,张亚男
1.油气资源与勘探技术教育部重点实验室(长江大学),湖北 武汉 430100 2.长江大学地球物理与石油资源学院,湖北 武汉 430100 3.中国石油集团长城钻探工程公司,北京 100101 4.长江大学图书馆,湖北 武汉 430100
近年来,中石油加大了对中东区块碳酸盐岩油气藏的开发力度,其油气勘探技术已成为学术界新的研究热点[1-3]。中东区块碳酸盐岩储层与国内塔里木盆地、四川盆地等碳酸盐岩储层差异较大,前者储集空间以孔隙为主,后者孔洞和裂缝比较发育[4,5]。尽管中东区块碳酸盐岩储层受裂缝和孔洞影响较小,但其孔隙类型复杂多样,储层非均质性强,给该区块储层参数评价带来较大挑战[6,7]。
准确评价渗透率对于储层开发方案的设计及产能预测十分重要。目前,国内外关于渗透率评价主要有3种思路:①通过岩石物理模型建立渗透率与孔隙度、比表面积和束缚水饱和度等储层特征参数的渗透率评价模型,如Wyllie-Rose方程[8]、Timur方程[9]及基于等效岩石组分理论的渗透率方程[10,11]等;②建立渗透率与测井响应参数之间统计模型,如渗透率与孔隙度、自然伽马相对值的统计模型[11]、神经网络算法模型[12-14]、核磁共振渗透率模型[15,16]和基于斯通利波的渗透率模型[17]等;③从压汞毛细管压力曲线中提取孔隙结构参数并建立与渗透率的统计模型[18-24],如Winland R35模型[22]、Swanson模型[23]和Capillary-Parachor模型[24]等。Winland R35模型、Swanson模型及Capillary-Parachor模型在碎屑岩或者成岩作用微弱的均一碳酸盐岩储层中应用效果较好,具有较大潜力,但在强非均质性碳酸盐岩储层中应用效果一般。Thomeer函数是对毛细管压力曲线拟合的一个数学表达式[25],该函数在中东区块复杂孔隙类型的碳酸盐岩储层孔隙结构定量表征中具有一定优势。由于渗透率主要受控于储层孔隙结构,为此笔者以Thomeer函数为基础,建立了一种新的渗透率评价模型,以提高中东区块碳酸盐岩储层渗透率的计算精度。
1 Thomeer函数及其参数提取
1.1 Thomeer函数
毛细管压力曲线是研究储层孔隙结构常用的手段之一,常见的用法是从毛细管压力曲线中提取平均孔喉半径、中值半径等表征岩石孔隙结构的参数,用来进行储层分类及储层参数的定量计算。目前有压汞法和半渗透隔板法2种方法可以获取储层岩石的毛细管压力曲线。
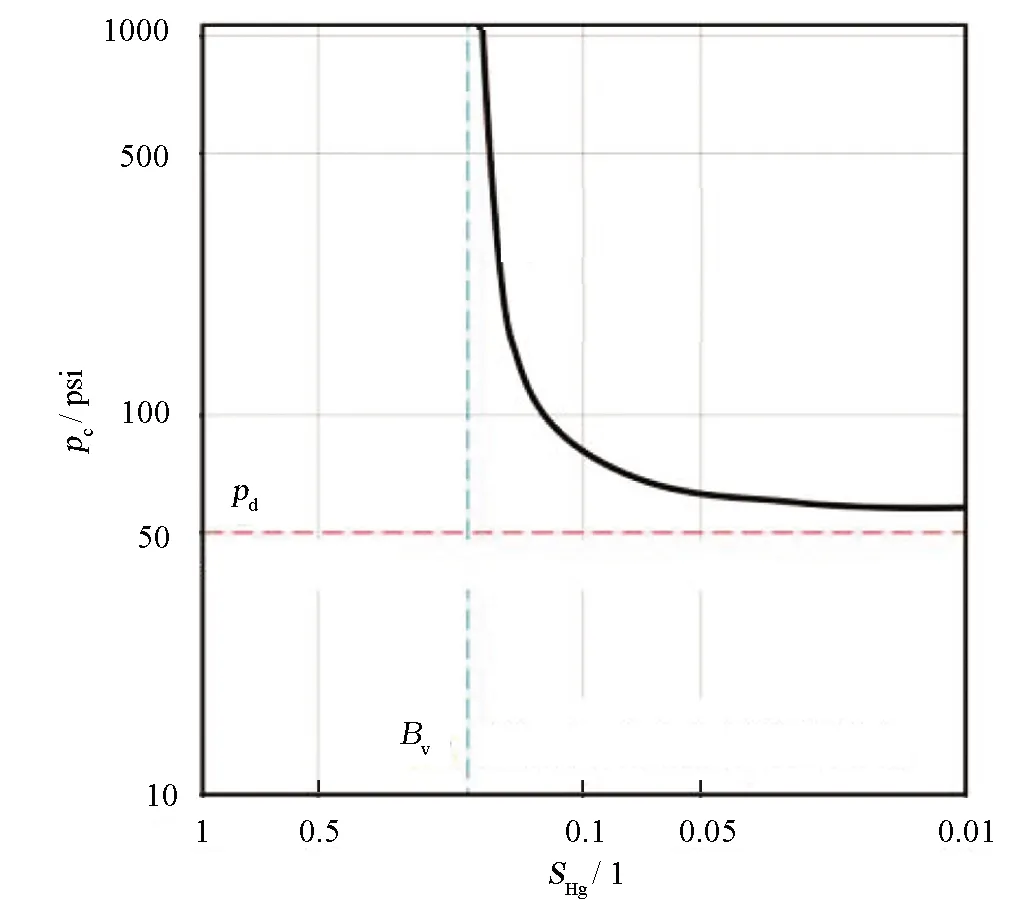
图1 压汞毛细管压力曲线双曲线形态特征 Fig.1 Hyperbola morphological characteristics of mercury injection capillary pressure curve
图1显示的是一组压汞毛细管压力曲线,在双对数坐标下,显示的是一种双曲线的数学关系,基于此,Thomeer提出了一个用来描述这种双曲线形态的方程[26]:
(1)
式中:SHg为进汞饱和度,1;VHg为毛细管压力无穷大时对应的进汞体积分数,1;pc为进汞压力,psi;pd为初始排驱压力,psi;G为孔隙几何因子,描述毛细管压力曲线弯曲的程度,反映孔喉的形态,1。
1.2 Thomeer参数提取
为了研究Thomeer参数与储层渗透率之间的关系,首先需要对压汞毛细管压力曲线进行Thomeer参数提取。笔者收集整理了中东区块H油田Mishrif层组1020块岩样的压汞毛细管压力曲线数据,发现其孔喉分布一般具有单峰、双峰和三峰3种形态。在双峰或三峰的孔喉分布曲线中,不同压力区间的进汞量代表某个孔喉大小相近且相互连通的同一孔喉体系的体积,即双峰形态的孔喉分布曲线表示有2个孔喉体系单元,三峰形态的孔喉分布曲线表示有3个孔喉体系单元,因此对于双峰或者三峰的压汞毛细管压力曲线,需要单独提取每个峰的G、pd和VHg。
Thomeer参数提取具体步骤为:首先,对压汞毛细管压力曲线进行麻皮校正;然后,采用变步长的牛顿阻尼迭代算法进行Thomeer函数拟合(见图2);最后,提取出Thomeer函数中的G、pd和VHg等参数(见表1)。需要强调的是,在对双峰和三峰进行拟合时,每个峰会相互干扰,函数极其难收敛,该研究尝试将双峰或者三峰中的每个峰相对拆开,并用收敛方向稳定的变步长的牛顿阻尼法进行迭代,解决迭代难收敛的问题。
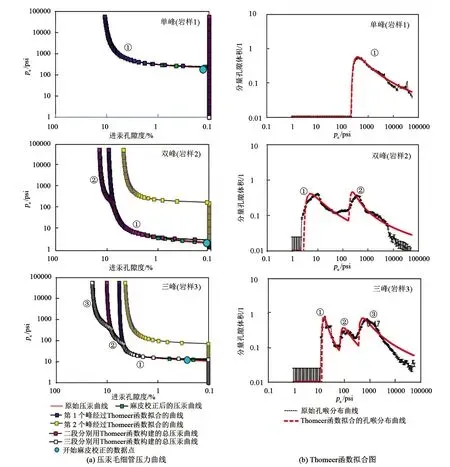
图2 孔喉分布分别为单峰、双峰及三峰时的Thomeer函数拟合图Fig.2 The Thomeer function fitting diagram of the pore throat distribution which is single peak,double peak and triple peak

表1 3块不同孔喉体系单元的岩样Thomeer参数提取
2 孔喉体系单元对岩石渗透率的影响
双峰或者三峰的压汞毛细管压力曲线中,每一个孔喉体系单元都对岩石渗透性起着作用。为了分析每个孔喉体系单元对岩石渗透率的影响,利用累计渗透率贡献公式(式(2))[27],在压汞孔喉分布图中绘制了累计渗透率贡献曲线:
(2)
式中:ΔKj为第j个点对应的渗透率贡献,1;rj为第j个点对应的孔喉半径,μm;SHg,j为第j个点对应的进汞饱和度,1。
图3显示的是2块岩样孔喉分布形态分别为双峰和三峰的孔喉分布曲线图及累计渗透率贡献曲线图。在图3(a)中,①号峰的累计渗透率贡献占比达99.7%,②号峰的累计渗透率贡献占比仅为0.3%;在图3(b)中,①号峰的累计渗透率贡献占比为97%,②+③号峰的累计渗透率贡献占比仅为3%。对于这2块岩样,①号峰的孔喉体系对岩样渗透率起主控作用。

图3 压汞孔喉分布曲线(双峰和三峰)中每个孔喉体系的渗透率贡献占比Fig.3 The permeability contribution ratio of each pore throat system in mercury injection pore throat distribution curve (bimodal and triple peak)
整理上述1020块岩样中的378块孔喉分布呈双峰形态和36块呈三峰形态的岩样压汞数据,分别计算了每个孔喉体系单元对整个岩石渗透率的贡献占比,统计结果如图4所示。
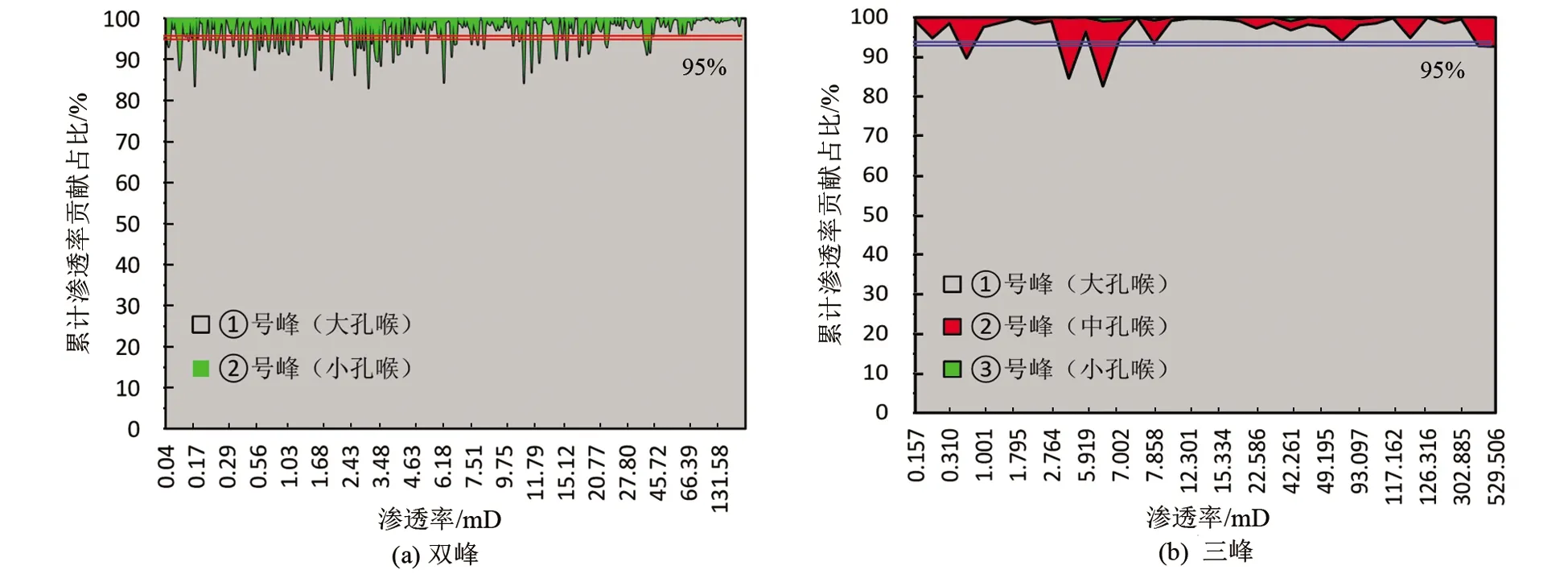
图4 孔喉分布为双峰和三峰的累计渗透率贡献占比统计Fig.4 The pore throat distribution contributes to the cumulative permeability statistics of the double-peak and triple-peak
从图4(a)中可以看出:孔喉分布为双峰的情况下,在渗透率区间为0.04~131.58mD之间的378块岩样中,孔喉半径区间最大的①号峰累计渗透率贡献占比基本大于95%,②号峰的影响可以忽略不计。图4(b)中显示:孔喉分布为三峰的情况下,在渗透率区间为0.157~529.506mD之间的36块岩样中,①号峰累计渗透率贡献占比基本大于95%,②+③号峰的影响可以忽略不计。说明无论是双峰还是三峰,对岩样渗透率起主要贡献的都是孔喉半径区间最大的孔喉体系单元。
3 渗透率模型
3.1 渗透率与Thomeer参数的响应关系
由于岩样渗透率的大小取决于孔喉半径区间最大的孔喉体系单元(①号峰),因此为了建立基于Thomeer函数的渗透率模型,笔者重点分析渗透率与①号峰G、pd和VHg的响应关系。
从上述1020块压汞岩样中随机选取了一口井的279块岩样(单峰249块,双峰11块,三峰19块)进行分析,分别建立了渗透率与pd、VHg、G的统计关系(见图5)。从图5中可以明显看出:渗透率与pd具有较好的幂函数关系,R2=0.7345;其次是VHg,R2=0.3681;与G的关系最差,R2=0.1019。
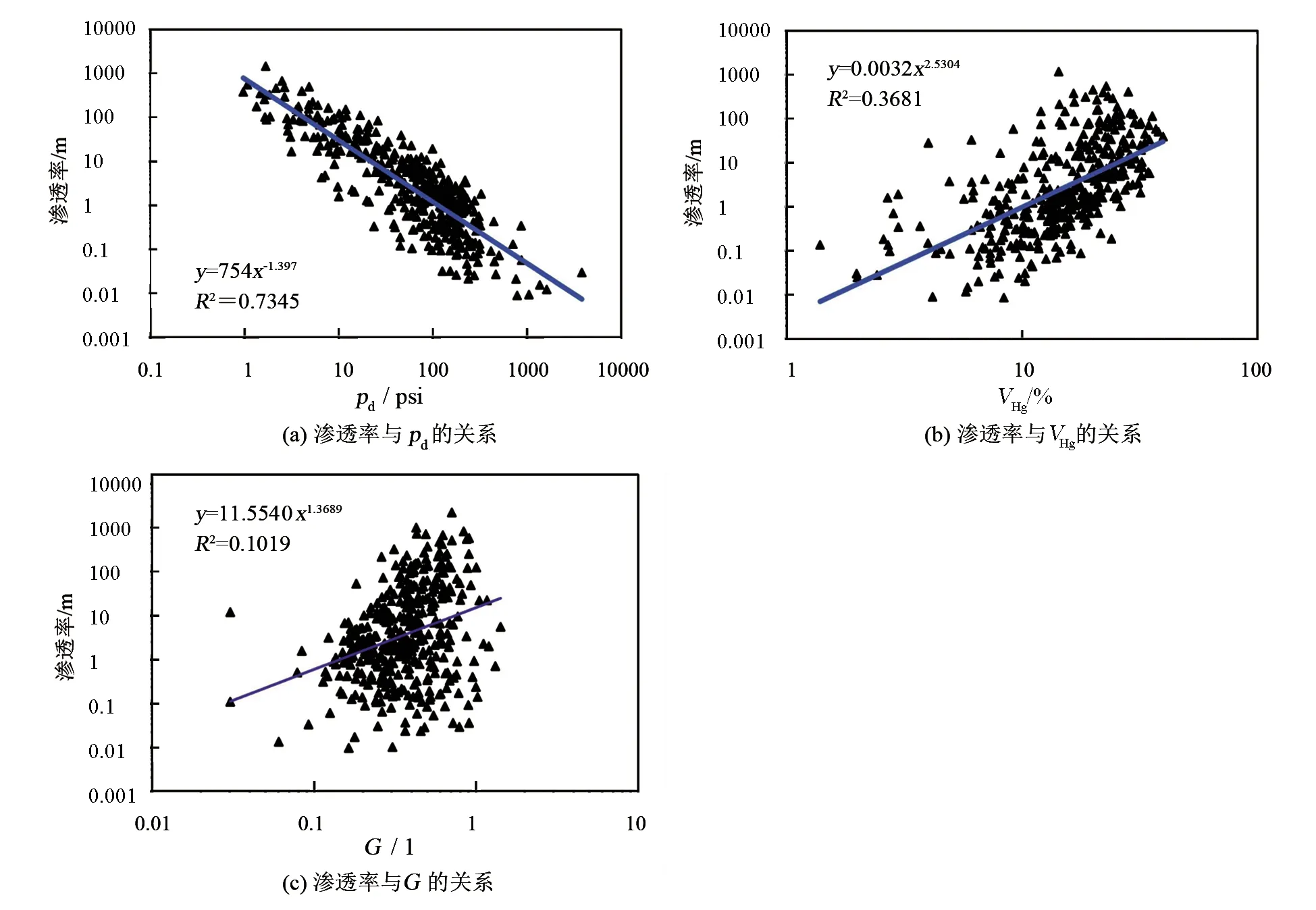
图5 渗透率与 pd、VHg、G的关系Fig.5 The relationship between permeability and pd、VHg and G
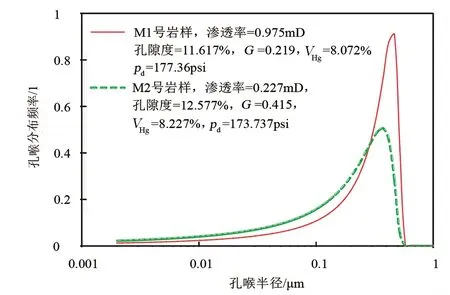
图6 pd和Bv相近,G不同的2块岩样孔喉分布对比Fig.6 Comparison of pore throat distribution in two rock samples with similar pd and Bv and different G
根据pc=2σcosθ/r(其中,σ为汞与空气的界面张力,θ为润湿角,r为毛细管半径)可知,pd可以转化为最大孔喉半径。在双峰或者三峰的压汞孔喉分布曲线中,由于②号峰和③号峰的孔喉体系单元对渗透率的影响可以忽略,根据VHg的定义,可以将其等效为岩样的有效流动孔隙度。根据上述统计分析结果,孔喉半径是控制渗透率大小的主控因素,其次是有效流动孔隙度。孔隙几何因子G表示孔喉分布形态的宽窄程度,反映了孔隙形状非均质性强弱程度,G越大,孔隙的非均质性越强。根据图5渗透率与G的关系发现,G似乎对渗透率的影响不大,但是,笔者选取了2块孔喉分布呈单峰的岩样,在pd、VHg相近,G不同的情况下,对比了其渗透率的大小(见图6)。M1号岩样pd=177.36psi,VHg=8.072%,与M2号岩样pd=173.737psi,VHg=8.227%相近,而2块岩样的孔喉分布形态差异却较大,分析其原因,M1号岩样G=0.219,孔喉分布形态较窄,其渗透率为0.975mD;M2号岩样G=0.415,孔喉分布形态较宽,其渗透率为0.227mD。说明在pd和VHg相近的情况下,孔喉分布形态越窄(G越小),渗透率越大,孔隙形状非均质性对渗透率的影响不能忽略。
3.2 基于Thomeer函数的渗透率模型
基于上述渗透率与Thomeer参数之间的响应关系认识,使用上述279块岩样压汞数据,建立了渗透率与①号峰G、pd和VHg的响应模型(见图7(a)):
lgK=-1.285lgpd+1.155lgVHg-
0.349lgG+1.185
R2=0.8177
(3)
将式(3)转换为幂函数形式为:
(4)
利用相同的数据,分别建立了基于Winland R35的渗透率模型(式(5),图7(b))、基于Swanson的渗透率模型(式(6),图7(c))及基于Capillary-Parachor的渗透率模型(式(7),图7(d)):
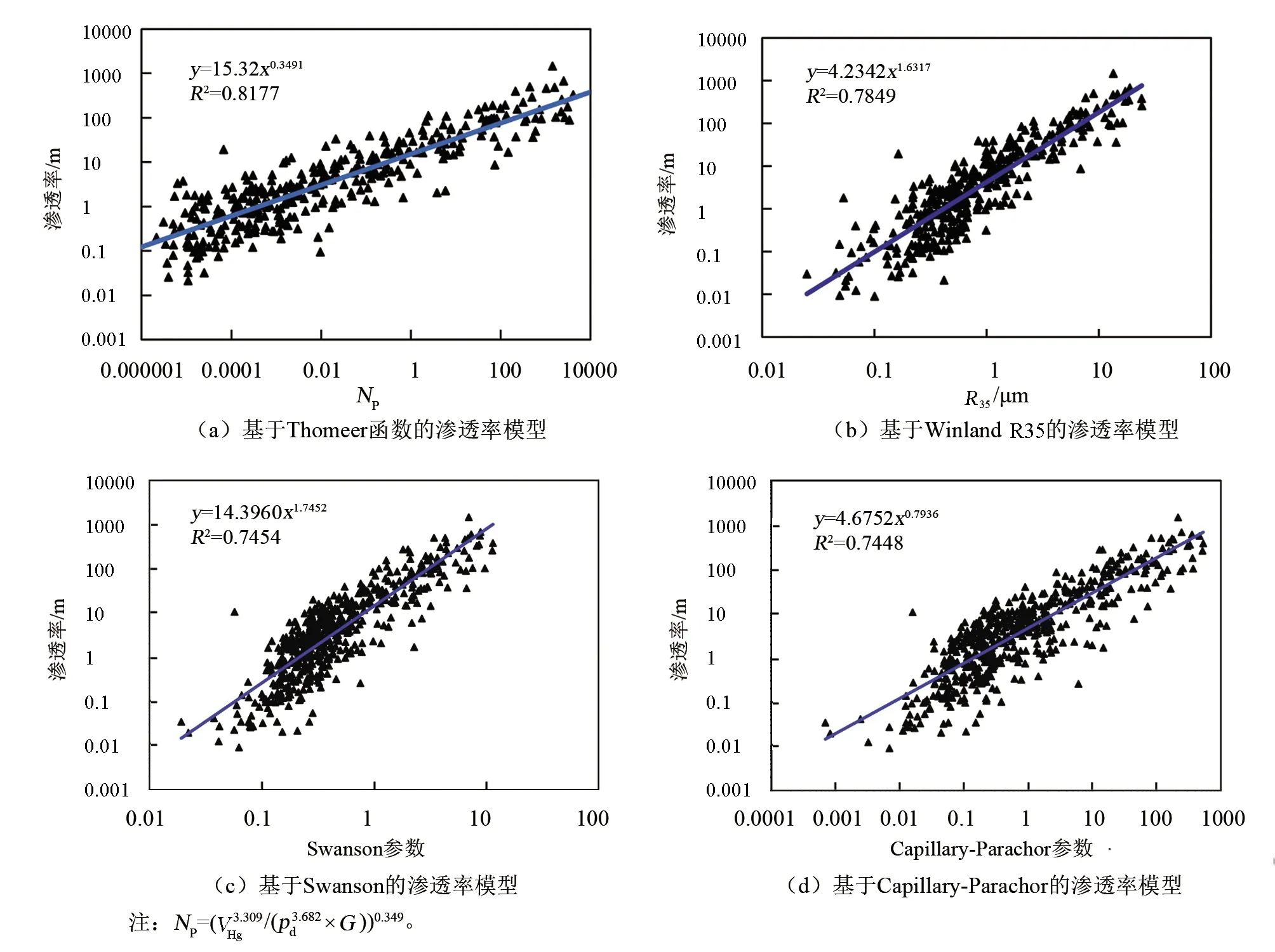
图7 4种基于压汞资料的渗透率模型Fig.7 Four permeability models based on mercury injection data
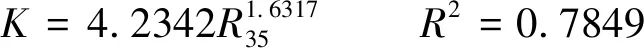
(5)
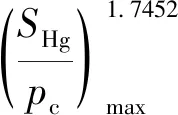
(6)
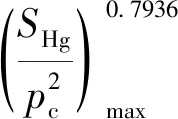
(7)
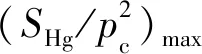
3.3 渗透率模型检验
从上述1020块压汞岩样中随机选取了另一口井189块岩样(单峰98块,双峰89块,三峰2块)进行渗透率模型精度分析,分别使用上述4种模型计算了其渗透率,并与岩心分析渗透率进行交会图对比(见图8)。从图8中可以看出,基于Thomeer函数的渗透率模型计算结果与岩心分析渗透率的误差较小,优于其他3种模型,特别是在低渗透区间,优势更加明显。
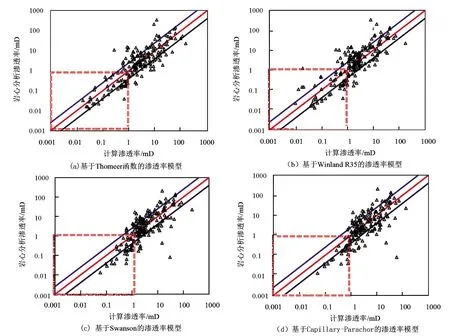
图8 4种渗透率模型与岩心分析渗透率效果对比分析Fig.8 Comparative analysis of four permeability models and core analysis permeability
4 结论
1)使用变步长的牛顿阻尼迭代算法,可以准确提取压汞孔喉分布曲线为单峰、双峰及三峰的Thomeer参数(G、pd和VHg),解决了迭代难收敛的问题。
2)对于双峰或者三峰的压汞孔喉分布曲线,对岩样渗透率起主要贡献的是孔喉半径区间最大的峰(孔喉体系单元);对于孔喉半径区间最大的孔喉体系单元,pd对岩样渗透率影响最大,其次是VHg和G。
3)建立了基于Thomeer函数的渗透率模型并应用于中东区块H油田碳酸盐岩渗透率的计算,其精度优于基于Winland R35的渗透率模型、基于Swanson的渗透率模型及基于Capillary-Parachor的渗透率模型。
