无刷直流电机RBF 神经网络滑模控制器设计

王 浩，白国振，刘世交

（上海理工大学机械工程学院，上海 200093）

0 引言

无刷直流电机是现代控制理论和现代电子技术融合的产物。作为由半导体技术衍生而出的机电一体化产品，无刷直流电机具有调速性能好、功率密度高、可靠性好且易于控制等优点［1-2］，因此在家用电器、汽车等诸多行业有广泛的应用。在多数应用场合中，传统控制方法能够满足系统性能要求，但是考虑到BLDCM 具有时变、多变量耦合等复杂特性，当系统受到外部干扰或系统参数发生变化时，传统控制方法难以对BLDCM 实现精确控制、满足高性能要求。

滑模控制（Sliding model control，SMC）对系统参数变化及外部干扰具有良好的鲁棒性和完全的自适应性，因此针对无刷直流电机的滑模控制策略研究较为丰富［3-7］。但是在实际应用中，由于控制作用来回切换、系统惯性和延迟及测量误差等影响因素，使结构控制在滑动模态下出现高频抖振，严重影响系统控制性能［8］。为了削弱系统抖振，研究者们提出滑模控制算法，如准滑动模态法［9］、干扰观测器法、滤波法、高阶滑模控制方法与分数阶滑模控制方法等［10］。上述控制方法在改善系统品质的同时依旧存在不足，如准滑动模态和干扰观测器使系统存在静态误差，高阶滑模控制算法实现较为复杂。

RBF 神经网络是一种先进的智能控制算法，具有较强的自学习、自适应、自组织功能，在处理控制系统非线性、不确定问题上有很好的应用前景［11-12］。RBF 神经网络具有良好的逼近能力、简单的网络结构和较快的学习能力［13-14］。文献［15］将RBF 神经网络应用于无刷直流电机无位置传感器控制；文献［16］构造了一个RBF 网络对无刷直流电机系统进行在线参数辨识、建立在线参考模型，由单神经元控制器完成控制器参数的自学习。

因此，本文将RBF 网络自适应算法与滑模变结构结合，设计RBF 神经网络自适应滑模位置控制算法，并优化控制系统中的趋近律和学习率，利用李雅普诺夫理论分析系统稳定性，最后通过系统仿真验证该算法对内外扰动均具有较强的抗干扰能力，且响应速度、位置精度和系统稳定性均有明显提升。

1 无刷直流电机数学模型构建

BLCDM 作为非线性机电元件，对其内部参数建立准确的数学模型难度较大。在建立数学模型前，需对电机模型作理想假设：BLDCM 为理想型，电机气隙磁感应强度呈方波分布，且忽略电机磁滞和涡流损耗、定子齿槽影响，以及电枢反应造成气隙磁场的影响，BLDCM 数学模型［17］构建包括：

（1）电压方程。其三相绕组电压平衡方程如式（1）所示。

其中，P为微分算子，即；Ua、Ub、Uc分别为三相定子电压；Ra、Rb、Rc分别为三相电机绕组电阻；ia、ib、ic分别为三相电机定子绕组电流；La、Lb、Lc分别为三相电机绕组自感；Lab、Lac、Lba、Lbc、Lca、Lcb分别为电机两相绕组间互感；ea、eb、ec分别为三相电机反电动势。

式（1）中，由于电机转子为永磁体，磁场强度恒定，且三相绕组相互对称，则认为电机两相绕组间互感为定常，BLDCM 三相绕组之间采用Y 型连接，根据基尔霍夫电流定律可知：

由式（1）、式（2）可得电压平衡方程为：

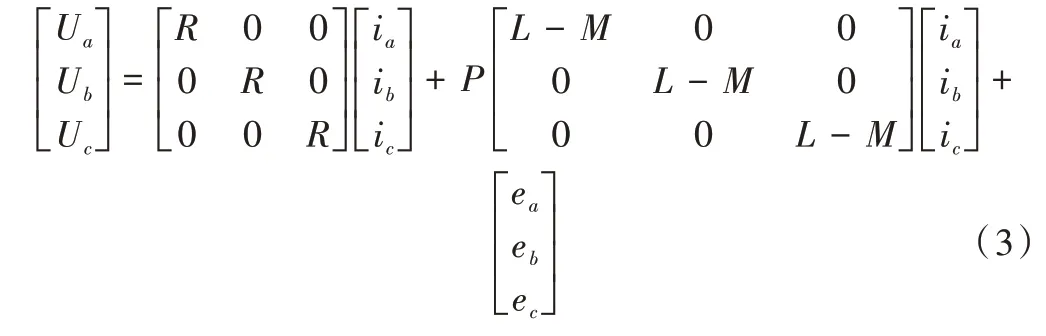
式（3）中L为定子绕组自感，M为定子绕组间互感。

（2）转矩方程。忽略电机功率损耗，所有电能均转化为动能，则电机电磁功率可表示为：

其中，Pe表示为电磁功率。

若忽略电机机械损耗以及电磁损耗，电机电磁功率可完全转化为电机转子动能［18］，则功率可表示为：

其中，ω表示转子角速度，Te表示为电机转矩。

根据式（4）、式（5）可推导出BLDCM 定子绕组的电磁转矩方程为：

BLDCM 通过Y 型连接，在任意时刻仅有两相导通，另一相闭合，导通两相绕组的电流与反电动势幅值相同，方向相反。式（6）可改写为：

其中，KT为转矩系数，i为电机绕组电流幅值。

BLDCM 反电动势幅值与电机转子角速度成正比例关系，电机绕组动态方程可表示为：

BLDCM 运动方程可表示为：

其中，TL为负载转矩，J为电机转动惯量，B为粘滞阻尼系数。

（3）传递函数。根据上述BLDCM 数学模型公式，可推导出传递函数方程。具体方程如式（10）所示。

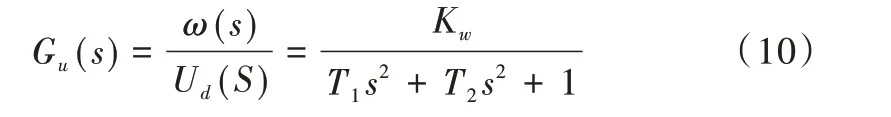
其中，Kw为系统增益，Ud为两相间平均电压，其中Kw、T1、T2可表示为：

2 控制器原理与设计

2.1 RBF 神经网络

径向基函数（Radical Basis Function，RBF）神经网络是一种具有单层神经元结构的神经网络，由Moody&Darken 提出，使用RBF 神经网络处理较隐性的规律时效率较高［19］。其结构可分为3 部分：①输入层，用于感知输入信号单元、实现输入信号到隐含层节点非线性映射；②隐含层，用于处理输入层信号；③输出层，用于处理隐含层信号，实现信号线性映射。其结构如图1 所示。

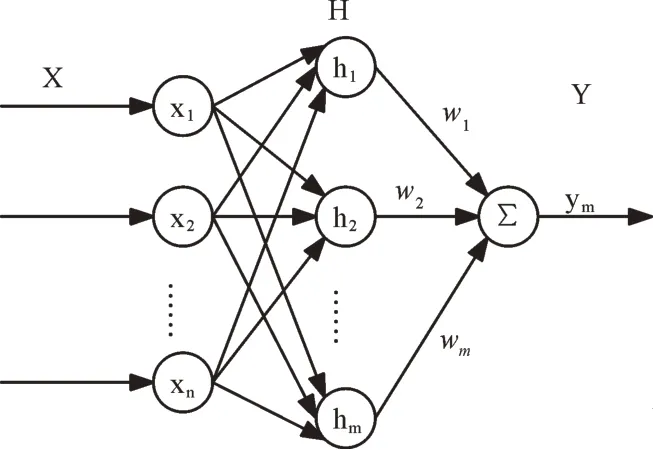
Fig.1 RBF network structure图1 RBF 网络结构

2.2 RBF 神经网络学习算法

其中，Xi为RBF 网络输入，σi表示为隐含层神经元宽度，输出层与隐含层之间为线性关系，通过加权参数调整，具体关系可表示为：

为了检测RBF 网络性能优劣，设目标函数为：

通过梯度寻优算法调节参数，式（13）和式（15）中节点基宽参数调整量Δδj和节点中心调整量Δcj的迭代算法如式（16）所示。

其中，η对应学习速率，α对应动量因子，二者取值范围为（0，1）。

2.3 RBF 网络自适应滑模控制器设计

滑模控制抖振是困扰学者已久的难题，造成抖振的主要因素之一是滑模控制器中控制策略的选择问题，在滑模控制策略的趋近律选择中，所用符号函数（sign）在趋向滑模面的过程中，使符号函数值在1 和-1 之间切换，控制器在趋近滑模附近出现抖振。

RBF 神经网络自适应滑模控制是将神经网络和滑模控制相结合、优势互补的方法。本文将神经网络替换滑模控制切换控制部分，由于神经网络具有自适应学习的能力，能够对负载和外界干扰进行自动补偿，所以RBF 神经网络自适应滑模控制能够锁定外界变化而自动调整，减小滑模控制中的抖振。

为提高无刷直流电机位置控制精度，考虑内部参数变化和外部负载变化情况，转矩平衡方程可表示为：

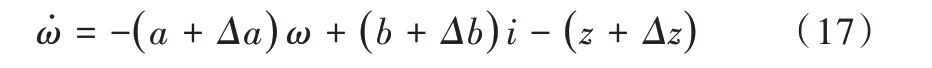
其中a=B/J，b=KT/J，c=TL/J，Δa、Δb和Δz为系统内部参数扰动与外部负载扰动造成的干扰变化量。

为使位置控制器相应角度θ较快跟踪设定角度θd，控制器位置跟踪误差可表示为e(t)=x1=θd-θ，根据式（17）可知：

根据式（18）可知，当e→0 时，可得→0，因此位置控制器满足设计要求。设滑模面切换函数为：

RBF 网络自适应滑模控制器系统结构可分为3 部分：滑模变结构控制器、RBF 网络和自适应律，控制系统结构，如图2 所示。

Fig.2 The structure of control system图2 控制系统结构

RBF 网络输入为x=[x1,x2]T，通过神经网络学习之后，不断改变权值大小，使输出函数逼近理想情况下的非线性函数f(x)。RBF 网络输出(x)分别为：

hf(x)为RBF 网络高斯函数，为加权向量。

为了进一步改善RBF 网络自适应滑模的抖振问题，对趋近律进行优化，优化后趋近律为：

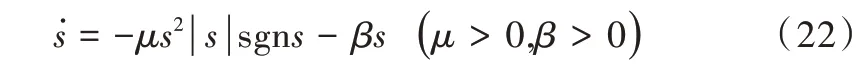
式（22）中趋近律可以分为幂次部分和指数部分，控制系统运动点与滑模面之间的距离较大时，s 值较大，此时指数部分和幂次部分同时起作用，因此趋近速度较快；当运动点靠近滑模面s→0 时，幂次部分趋近于零，仅指数部分起作用，此时符号函数sgns造成抖动的影响也随着幂次部分减小而消减。因此本文设计趋近律在保证收敛速度的同时，也使控制系统动态响应更加平稳。

根据式（18）、（21）和（22）可得控制律为：

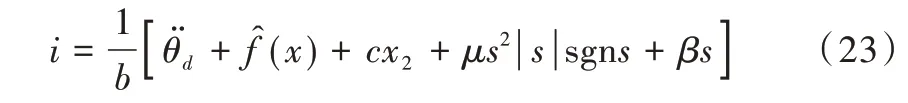
2.4 自适应学习速率

RBF 神经网络在学习的过程中，采用梯度下降法，在权值w的更新过程中，学习速率η设定为固定值，会造成学习效率低和收敛速度慢等问题。为了提高学习效率和收敛速度，采用自适应学习速率在线调整学习速率，在保证系统稳定和学习过程稳定的条件下，以尽可能高的学习速率进行学习。本文根据递推误差(k-1)2的大小调整学习速率，具体调整规则为：

其中γ1,γ2,γ3为比例常量。

2.5 稳定性分析

设计Lyapunov 函数为：

εf为RBF 逼近误差。

将式（23）控制律代入到切换面导数可得：

将式（27）带入式（25）可得：

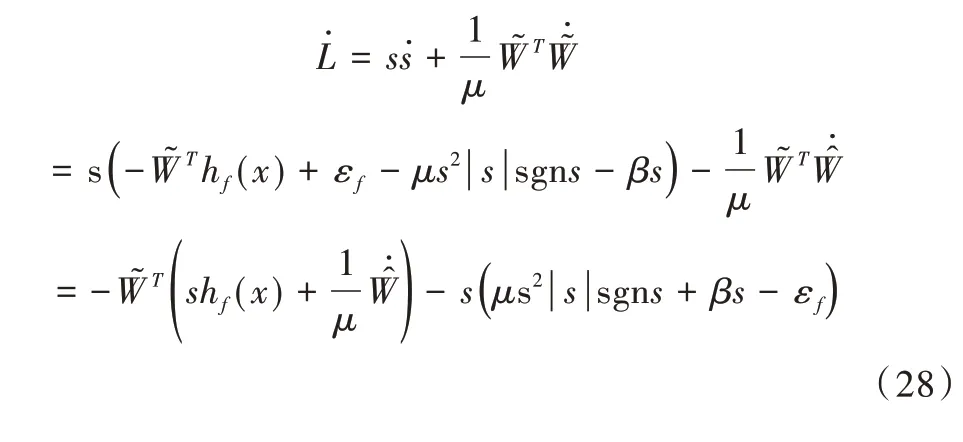
设神经网络自适应律为：

将式（29）带入式（28）中可得：

根据式（30）可知，由于εf是一个非常小的实数，因此对于任意范围的s，均有≤0，满足了Lyapunov 稳定条件，因此控制系统是稳定且收敛的。

3 仿真实验

3.1 仿真实验设计

为验证RBF 神经网络自适应控制器RBF 位置控制算法有效性和优越性，在MATLA/SIMULINK 实验平台中搭建BLDCM 仿真模型，并与传统PID 控制和SMC 控制进行对比分析。BLDCM 主要参数如表1 所示。

Table 1 Parameters of brushless DC motor表1 无刷直流电机参数

在MATLAB/Simulink 平台中，搭建基于RBF 神经网络的BLDCM 模型，电流环为内环，采用PI 控制，外环为位置环，RBF 网络自适应滑模位置控制器如图3 所示。

3.2 仿真结果与分析

为验证本文控制算法优越性，将RBF 网络自适应滑模位置控制算法与分数阶滑模控制（FOSMC）、传统滑模控制（SMC）以及传统PID 控制进行仿真对比。为保证对比仿真有效性，将这4 种控制方法运用于双闭环控制系统速度环，且电流环均使用PI 控制器，电机参数相同保持不变。

对于连续变化的位置指令跟随性，设定位置正弦曲线周期为1.6s，幅值为10°，仿真时长为5s。分别对比PID 控制、滑模控制和改进的RBF 神经网络自适应控制算法，仿真结果如图4 所示。

从图4（a）、（b）两种控制的跟随曲线分析中，SMC 控制算法在外干扰的影响下，最大误差为0.020 1°，稳定误差区间为-0.006 7°～0.006 6°，RBF 网络自适应滑模位置控制算法依然可以很好地跟随设定的正弦曲线，跟随性较好。

对于一个阶跃的控制信号，设定位置指令于0.1s 处，幅值从0°变化至10°，仿真时长取0.5s。分别再用PID 控制、SMC 控制、FOSMC 控制及RBF 网络自适应滑模控制进行仿真，仿真对比分析如图5（彩图扫OSID 码可见）所示。

Fig.3 Simulation structure of BLDCM system图3 BLDCM 系统仿真结构

Fig.4 Comparison of position following图4 位置跟随对比

从图4 仿真对比分析可知，PID 控制算法控制效果较差，PID 控制于0.24s 处进入0.26s 的振荡期，振荡幅度由1.245%衰减到0，而超调量为13.2%。SMC 控制器在外干扰的作用下，也产生衰减振荡，于0.18s 进入0.27s 的振荡期，振荡幅值由0.9%衰减至0，超调量为6.2%。FOSMC 控制于0.15s 进入0.18s 的振荡期，振荡幅值从1%衰减至0，超调量为0。RBF 网络自适应滑模位置控制算法0.155s 处开始收敛，然后进入0.085s 的振荡期，最后进入稳定收敛阶段，在收敛过程中无超调量。相比于PID 控制、SMC 控制和FOSMC 控制算法，RBF 神经网络自适应滑模位置控制算法鲁棒性高，收敛速度也较快（见图5）。

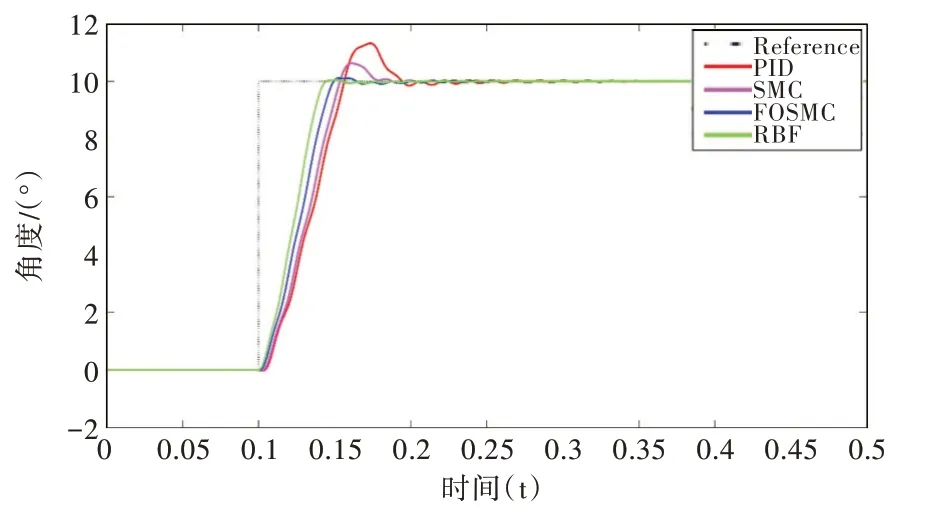
Fig.5 Simulation comparison of control algorithms图5 控制算法仿真对比

4 结语

本文在分析神经网络和滑模控制算法优缺点的基础上，提出了一种无刷直流电机的RBF 网络自适应滑模控制策略，将RBF 神经网络引入到直流电机控制系统中，能够提高系统稳定性与抗干扰性，同时还具有非线性能力和自学习能力；与滑模控制算法相结合，削弱了滑模控制算法存在抖振的缺点，使系统具有良好的鲁棒性和自适应性。通过仿真实验验证了RBF 神经网络自适应滑模控制性能更佳，其响应速度、位置精度和系统稳定性均得到相应提升。但在神经网络控制系统设计中，其网络结构设计和学习方法的选择还有待于进一步研究。