一种2 维内核与3 维内核极化码的凿孔算法

陈 晨

（中国联合网络通信有限公司济南软件研究院，山东济南 250000）

0 引言

随着第五代移动通信技术（5thGeneration，5G）的发展，对通信系统传输速率及传输可靠性的要求更高。香农第二定理［1］证明，信息传输速率在小于信道容量的前提下，通过合理的信道编码可以提高传输速率，实现更可靠的传输。极化码就是第一个被严格证明可在二进制离散无记忆信道（Binary-Discrete Memoryless Channel，B-DMC）下达到信道容量的编码方法。

早期的信道编码技术是把信息序列划分成不同的组，每组中增加冗余比特表示信息比特之间的代数关系。1949 年，第一个实用的差错控制编码方案是由汉明（Rich⁃ard Wesley Hamming）提出的汉明码（Hamming Code）［2］。汉明码一组包含4 个连续的信息比特，将组内4 个比特之间的线性组合用3 个比特表示，并将计算结果放在4 个比特后面一同发送。汉明码最多可纠正1 个比特的错误或检测出2 个比特的错误。弗兰克·格雷（Frank Gray）在1953 年提出了格雷码（Gray Code）［3］。格雷码是通过对每个码字增加一位总的奇偶校验位进行扩展，连续的两个数只有一个位元变化。由于这种特性，格雷码目前常用于数字信号与模拟信号之间的转换。1954 年，Reed［4］和Muller［5］提出通过分组保证最大码字距离的RM 码（Reed-Muller code）。BCH 码是由Hocquenghem［6］和Bose 等［7］在20 世纪60 年代分别独立发明的码字，其具有的循环特性可纠正多个错误符号。BCH 码在卫星通信和磁盘驱动器等领域作出了重要贡献。Reed 和Solomon［8］在1960 年发明RS 码（Reed-Sol⁃omon code）。RS 码是一种前向纠错的编码方式，该码字目前常应用于商业的光碟领域。

随着信道编码技术的发展，概率编码成为了研究热点。概率编码不是寻找较大的码字距离，而是设计一种平均性能最优且复杂度较低的码字。1954 年，Elias［9-10］提出乘积码，第二年又提出卷积码（Convolutional code），通过依次连续地进行编码，编码器的输出与此刻以及之前的输入都有相关性；1966 年，Forney［11］提出级联码，首先将简单的短码单独进行编码作为内码，然后将内码串行级联构成长码作为外码，并对外码继续编码。在级联的思想下，1993年，法国教授Berrou 等［12］在日内瓦举行的国际通信大会（ICC）上提出一类称为Turbo 码的并行级联码，开启了Tur⁃bo 码研究的热潮。Turbo 码中的两个编码器分别进行编码，并将编码结果通过伪随机的交织方式并行级联。译码时为了缓解门限效应，两个解码器之间进行迭代译码，译码过程与涡轮增压的工作流程相似，所以被称为Turbo 码。Turbo 码也被应用于3G 和4G 蜂窝网络。

1962 年，Gallager［13］提出低密度奇偶校验码（Low Den⁃sity Parity Check Code，LDPC），因无法实现译码，1981 年Tanner［14］通过Tanner 图更形象地解释了LDPC 的译码步骤。1996 年，MacKay 等［15-16］实现了LDPC 的译码，同时延伸LDPC 的思想提出非正则的LDPC 码，性能甚至超过Tur⁃bo，一度成为性能最佳的编码方案。LDPC 码具有译码复杂度低、码率灵活、具备更低的错误平层（Error Floor）等优点，在较大容量的通信以及对误码率要求苛刻的环境中表现优异。但LPDC 硬件资源消耗大，编码复杂度高。

虽然Tanner 图的发现可帮助编码研究人员更形象地分析编码过程，但是仍然没有发现容量可达的编码方案。土耳其Bilkent 大学教授Arikan［17-18］发现信道容量通过一系列信道变换会产生两极分化的效果，并利用这一现象提出极化码（Polar Codes）。极化码可在码字无限长的情况下，经过B-DMC 信道进行传输，其是信道容量可达的。极化码一经提出就受到全世界瞩目，众多学者不断对极化码进行研究与改进。如今极化码的性能已与LDPC 码和Tur⁃bo 码相近，甚至更好。极化码结构简单，具有编译码复杂度低、低延迟等特点，更符合未来5G 的要求。2016 年，美国当地时间11 月17 日，经过中国华为等公司的努力，极化码成为了5G 标准之一。

虽然极化码结构简单、编译码复杂度低，但有限的码长令极化码的极化效果不够显著，若要使用这些信道进行信息传输，译码性能会有所损失［19-20］。由于极化码需要进行信道极化操作，结构比较固定，码长不够灵活，所以当码长与实际需求不匹配时，需要对极化码进行凿孔操作。但当母码码长较长，需要凿孔的比特则有可能增多，从而增加编码复杂度以及译码的性能损失。本文通过实现码长更灵活的多维内核极化码，减少凿孔比特个数，提出基于多维内核极化码的凿孔算法，并建立多维内核极化码的凿孔算法模型。该算法相比基于2 维内核极化码的凿孔算法具有更好的性能，因此对于多维内核极化码的实际应用具有重要意义。

1 基于2 维内核与3 维内核极化码的凿孔算法

文献［21］提出一种使用2 维内核与l维内核混合构造的可灵活实现码长的极化码。在信道极化过程中，不再固定使用两个信道进行信道合并操作，而是使用ns信道在相应位置进行信道合并与信道分割操作。信道极化过程中需要使用不同维度的内核，每个ni都对应一个ni×ni内核矩阵Tni，则生成矩阵为GN≜Tn1⊗…⊗Tns，此时N个码字序列x可通过x=uGN获得。当Tni的顺序不同，生成矩阵不同，极化码的极化效果也不同。以2 维内核和3 维内核为例，将T3放在最靠近发送端的一端，构造2 维内核和3 维内核混合的极化码。以（6，3）极化码为例，将信道极化过程分为两阶，并建立生成矩阵，如式（1）所示，对应的编码结构如图1 所示。

相比Arikan 提出的极化码，在接收端x与y是通过反序重排进行映射以节省硬件资源，而多维内核极化码是通过经典排序算法得到信道输入端与输出端的对应关系，其排序算法是从接收端开始，将每次的排序结果用矩阵Pi表示，则最终排序结果为P1。由原始极化码可知，最终排序结果是通过每个RNi进行排序得到的，其中，接收端对应发送端的序列则是所有RNi的逆操作。在多维内核中，接收端序列是所有Pi结果的逆操作，即P1=(P2…Ps)-1。每一阶的Pi(i＞1) 可通过Pi=(Qi|Qi+Ni+1|…|Qi+(N/Ni+1-1)Ni+1)得到，最后一阶的排序结果Ps=Qs。其中，Qi计算公式如下：

Fig.1 Encoding structure of multi-kernel polar code for G6= T2⊗T3图1 G6= T2⊗T3的多维内核极化码编码结构

以N=6 的极化码为例，若要获得接收端与发送端的对应位置，先计算P2，具体公式如下：

使用不同的3 维内核进行信道极化，编码结构也不同，本文后续的T3表示方法均使用式（4）。

2 算法设计

在实际应用中，当确定极化码的K个信息比特时，如何调整编码速率以满足物理信道的信道容量是一个重要问题。虽然可通过使用多维内核以低复杂度实现更灵活的极化码码长，但对于极化码而言，编码时信道极化每一阶的结构固定，仅通过多维内核的调整无法实现任意码长。凿孔算法可实现极化码的任意码长，并解决了码率适配等问题。

2.1 构造方法

极化码通过N个独立的信道经过信道合并操作引入相关性，并使用其中的M个信道进行传输。不传输信息的信道是一个容量为零的虚拟信道，故凿孔比特的个数m=N-M。

设信道接收错误的概率为p，通过T3所处的阶进行编码，每个子信道传输错误的概率分别为1-(1-p)3、1-(1-p) -(1-p)2+(1-p)3和1-2(1-p)+(1-p)2。在BEC 信道下，p=Z(W),I(W)=1-Z(W)，经过信道极化后，信道容量计算公式如下：

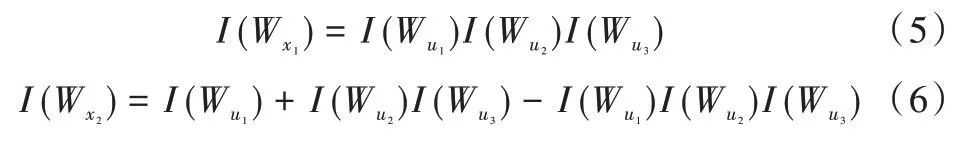
通过公式计算，若T3内核与T2内核传输凿孔比特，当且仅当第一个信道或全部信道都进行传输时，才能满足信道容量守恒和凿孔信道收发两端信道容量同时为0 的要求。

在噪声方差为δ2的AWGN 信道下，假设发送全零序列，则对数似然比为：

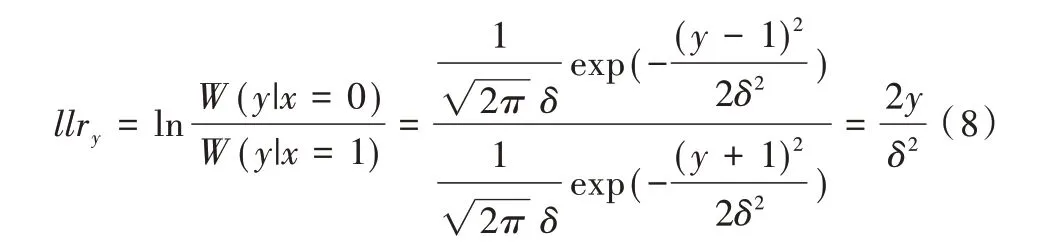
假设llr值的概率密度函数为，通过分析llr值计算公式，得到使用T3的高斯近似递归公式如下：

则SC 译码的误帧率（BLER）上界如下：

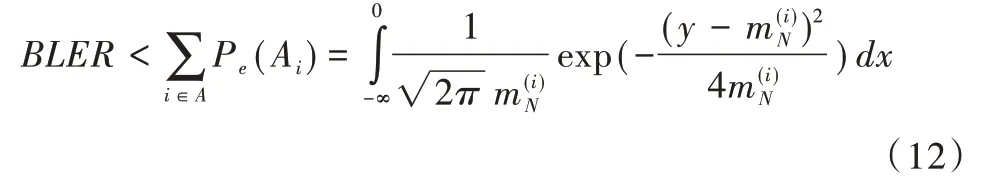
在2dB 的情况下，在T3内核中传输一位凿孔比特，通过计算得到各子信道的错误概率如表1 所示。当传输一个凿孔比特时，凿掉T3中的第一个信道可获得最小的错误概率。

Table 1 The error probability of subchannels for T3after puncturing one bit表1 T3内核凿掉一个比特后各子信道错误概率

当使用T3内核编码进行信道极化后，根据经典排序算法，将每个3 维内核中的第一个信道连续地排序到前Nv3，在此集合中选择信道传输凿孔比特，则可保证收发端传输凿孔信道的对应关系。此时发送端的凿孔方案可描述为：若使用2 维内核和3 维内核极化码执行凿孔算法，依次使用T3内核中的第一个信道传输凿孔比特。

2.2 信息位选择

极化码作为一种线性分组码，码的最小距离对译码性能有着重要影响。在执行凿孔算法后，由于m 个信道传输凿孔比特，此时将虚拟信道在生成矩阵中对应的行和列全部置为0，重新计算距离谱，从中选出K 个最大的最小距离对应序号，并使用相应位置的信道传输信息。当凿孔比特m∈[1/4 ⋅N,1/2 ⋅N]时，在发送端将T3中的第一个信道用来传输凿孔比特，此时执行凿孔后的最小距离谱如下：

在T3内核中选择u1传输一位信息比特，选择u1和u2传输两位信息比特。重新构造生成矩阵时，未经过排序的最小距离谱为=(2,1)⊗(n-2)⊗。若在接收端执行凿孔算法，利用前m个信道传输凿孔比特，得到接收序列=(p1,…,pm,…,pN)，通过排序算法得到发送端执行凿孔算法的发送序列ℬ=⋅P1。从距离谱中选取K个最大的最小距离对应序号放入集合I，集合I就是凿孔后的信息集合，具体算法如下：

2.3 性能分析

本文建立2 维内核与3 维内核模型，在AWGN 信道下进行仿真，采用BPSK 进行调制，发送10 万帧测试数据，构造了（72，36）极化码和（192，96）极化码，生成矩阵分别为。

对于（72，36）极化码，在2dB 下分别通过高斯近似和距离谱选取信息集合A的性能曲线对比如图2 所示。图中分别给出在SCL8 译码器下BER 与BLER 的性能，由性能曲线可知，通过距离谱选取的信息集合极化码BLER 性能优于高斯近似选取的信息集合，但BER 的性能没有得到提升。当BLER=10-3时，会有0.8dB 左右的增益。

图3 为（191，96）极化码的性能曲线，其中（191，96）极化码是基于（192，96）多维内核极化码通过执行本文提出的凿孔算法得出的。由性能曲线可知，当BLER=10-4时，基于多维极化码的凿孔算法有0.55dB 左右的增益。

Fig.2 Performance curve of selection information set A GA and distance spectrum图2 高斯近似与距离谱选取信息集合A 性能曲线

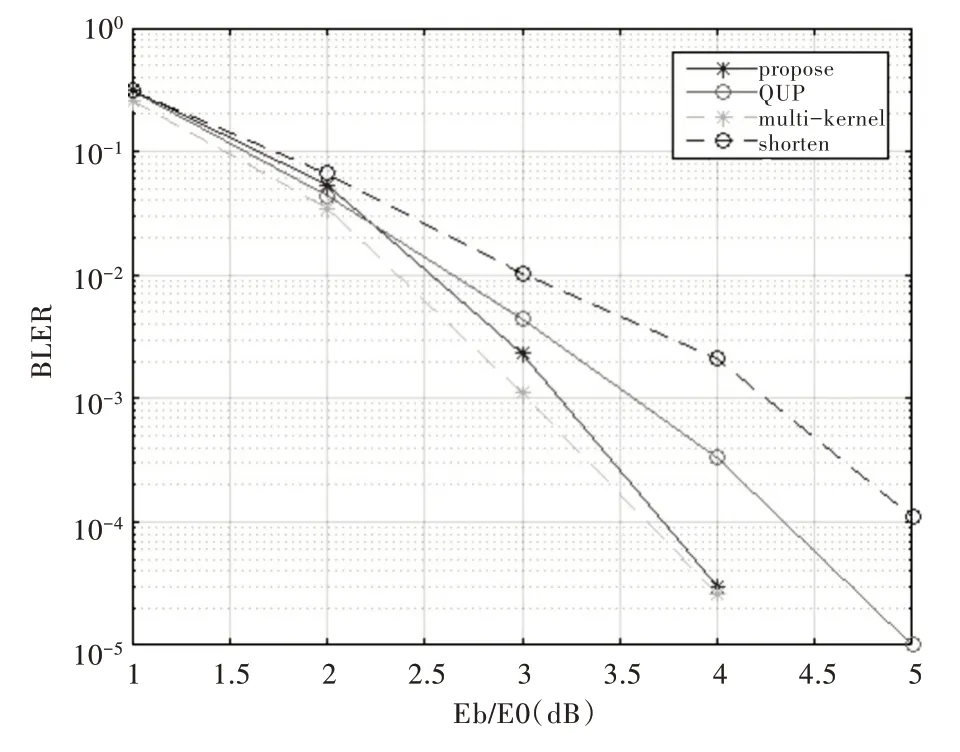
Fig.3 The performance curve of（191，96）polar code图3（191，96）极化码性能曲线

3 总结与展望

本文对2 维内核与3 维内核极化码进行了深入研究，通过发送端和接收端传输凿孔比特信道的对应关系获得凿孔模式，从而实现任意码长的极化码。在执行凿孔后的生成矩阵中重新计算距离谱，重新选择最大的最小距离信道作为信息集合A。实验结果表明，基于多维极化码的凿孔算法与基于原始极化码的凿孔算法具有相似的性能，甚至超过了基于原始极化码的凿孔算法性能。

随着数字时代的发展，人们对移动通信的要求越来越高。极化码是近年来信道编码领域的研究热点之一。本文在实现更灵活的码长和码率方面进行了一定改进，但多维极化码的编译码仍有改进的空间。在构造多维内核极化码时，高维内核处于不同的阶，对极化码的性能有着很大影响。为获得更好的译码性能，需要对高维内核编码时处在什么位置等问题作进一步研究。