基于多尺度排列熵的睡眠阶段阈值研究

骆金晨，邹任玲

（上海理工大学医疗器械与食品学院，上海 200093）

0 引言

如今睡眠障碍已成为抑郁症、脑卒中、精神分裂等高发疾病的临床表现之一［1］。研究表明，患有失眠症的患者较健康人的抑郁症患病风险高出10 倍［2］，有超过90% 的抑郁症患者患有睡眠障碍疾病［3］，并且脑卒中患者睡眠障碍的形成会使疾病加重［4］，故进行睡眠阶段脑电相关研究将有助于抑郁症、脑卒中等疾病的早期诊断。根据美国睡眠医学学会（AASM）制定的指南，将睡眠阶段分为W 期、N1 期、N2 期、N3 期和REM 期。脑电信号（Electroencepha⁃logram，EEG）具有明显的非平稳性和非线性特点［5］，近年来，对EEG 信号提取非线性动力学特征以提高睡眠分期识别准确率成为该领域的研究方向之一。其中，具有代表性的研究成果有：Khald 等［6］对睡眠EEG 信号分别提取平均Teager 能量、平均曲线长度以及Hurst 指数特征，经决策树分类器分类得到89.06% 的识别率；Fan［7］通过对睡眠脑电主成分进行分析，并提取多尺度熵，经BPNN 分类得到87.9% 的识别率；杨芳等［8］通过对睡眠脑电信号分别提取脑电能量特征和模糊熵特征，经支持向量机分类得到88.45% 的识别率。

在睡眠阶段分期研究中，研究者主要集中于选择特征向量类别以提高分类准确率，而忽视了对所选特征进行定量分析。多尺度排列熵（Multiscale Permutation Entropy，MPE）作为一种非线性分析方法，对刻画信号复杂度具有良好的适应性，目前已开始应用于人体生理信号、车辆振动等非平稳、非线性信号研究中［9］。因此，本文引入MPE 方法用于睡眠各期阈值研究。

1 实验源数据

本研究实验数据采用MIT-BIH 中的Sleep-EDF 数据集，受试者年龄均在21～35 岁之间，其中标记为sc*的实测数据是从睡眠健康受试者身上获取的，标记为st*的实测数据是从有轻微入睡困难症的受试者身上获取的。采集的数据包括脑电信号、眼电信号（Electrooculogram，EOG）、肌电信号（Electromyography，EMG）等7 项数据，EEG 信号记录电极分别为Fpz-Cz 和Pz-Oz，都在受试者未服用任何药物的前提下测得，其采样频率为100Hz，信号幅值单位为uV。研究表明，采用Fpz-Cz 导联数据作为睡眠分期结果更加准确［10］，为了更好地与其它文献相比较，在研究中EEG 信号最终采用Fpz-Cz 通道数据。专家们对脑电图数据每30s 进行一次人工标记，标记结果以hyp 格式文件进行存储。因此，将EEG 信号以30s 时间间隔作为时间窗，逐段截取3 000 个采样点片段，从中选取近2h 的有效数据作为研究样本集。

2 睡眠脑电信号预处理

EEG 信号作为人体生理信号中的一种，常因混有其它信号导致信号弱、噪声强，因此需对原始脑电信号进行预处理去噪。小波包变换和数字滤波器作为两种分析非平稳信号的典型方法，前者可同时对信号低频和高频分量进行细分，后者可剔除固定频段以外的信号源。因睡眠EEG信号主要集中在35Hz 以下，故本研究基于小波包理论与数字滤波器方法原理进行去噪处理。以sc4002e0 受试者为例，选取db3、db4、db5、db10、coif4、coif5 5 种EEG 信号常用的小波基函数和3～8 的常用分解层数，探究合适的小波基函数及分解层数。选用信噪比（SNR）和均方误差（MSE）两个指标评价去噪效果，SNR 越大，说明信号含有的噪声量越小，MSE 越小，说明信号失真度越低，更接近原始信号。通过对比试验发现，对EEG 信号进行db10 小波基函数3 层分解可获得最大的SNR 和最低的MSE。对小波包去噪后的样本采用FIR 等波纹低通滤波器进行0Hz～35Hz 低通滤波，其参数设置如下：通带截止频率为35Hz，阻带截止频率为37Hz，通带衰减为1db，阻带衰减为40db，密度因子为20。图1 为W 期30s 信号去噪前后时域对比图，从图中可以看出，滤波后的信号较滤波前毛刺明显减少（彩图扫OSID 码可见）。

Fig.1 Comparison of sleep EEG signal before and after preprocessing图1 睡眠脑电信号预处理前后对比

3 多尺度排列熵优化设计

3.1 排列熵算法参数设计优化

排列熵（Permutation Entropy，PE）是基于香农熵未考虑时间信号序列值之间的时间关系而提出的一种快速、简单的算法［11］。其优点在于能有效抵抗噪声信号干扰，且对信号敏感性强、鲁棒性较好，仅对相邻数值进行比较，从而减少计算时间，现已广泛应用于机械工业［12］、生物医学［13］及金融［14］等领域。针对N 个采样点的时间序列{x(i),i=1,2,3,…N}，其算法步骤如下［15］：

（1）对信号x（i）进行相空间重构处理，得到如下相空间重构矩阵，该矩阵包含k 个向量，每个向量共有m 个点。

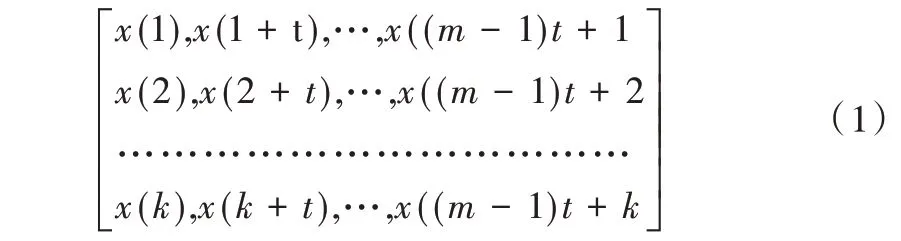
其中，t 为时间延迟，m 为嵌入维数。

（2）对相重构矩阵k 个重构向量的m 个点进行升序排列，即可得：

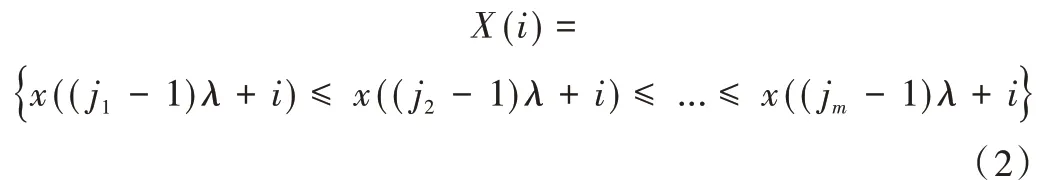
其中，i 表示相重构矩阵的第i 个向量，1 ≤i≤k。

（3）排序后相重构矩阵获得k 组符号序列，每组序列里共有m 个符号，其中所得符号序列为m！中的一种情况，任意一个向量X（i）的符号序列为{j1,j2,j3,…,jm}。

（4）计算上一步得到的每种符号序列出现的频率，所有符号序列出现概率之和始终为1。根据香农熵定义形式，可将时间信号序列{x(i),i=1,2,3,...N} 的排列熵定义为如下形式：

（5）对PE 进行标准化操作，标准化后Hp(m) 值范围在0～1 之间，其主要反映信号的随机性，即Hp值越大，信号随机性越强。

在实际计算时间序列PE 值的过程中，需要输入时间延迟t、嵌入维数m 以及信号长度N 共3 个参数值［16］。本研究中对每个样本以30s 的时间间隔进行截取，信号采样频率为100Hz，故每个样本信号长度N 均为固定值3 000。排列熵的计算量主要集中于相空间重构过程中k 个重构向量的m！全排列［17］，因此在满足要求的前提下，选择合适的序列点间隔和时间延迟非常重要。

以一名受试者的W 期睡眠脑电信号为例，时间延迟t值取1～8，不同嵌入维数m 和PE 值变化曲线如图2 所示（彩图扫OSID 码可见）。从图中可以看出，8 条曲线整体呈下降趋势，说明时间延迟t 对计算睡眠脑电排列熵值的影响程度偏低。其中，时间延迟t 为1 的曲线与其它7 条曲线区分明显，所以t 值不可取1，又因排列熵的计算时间与时间延迟呈正相关，故在取得相同计算结果的前提下，较长的时间延迟所需计算量也随之增加，因此本研究取时间延迟t 为2 较为合适。以t 值为2 的曲线为例，曲线下降斜率随尺度因子的增加而逐渐加大，说明较小的尺度因子对PE 的熵值影响较小，而较大的尺度因子对PE 的熵值影响较大。

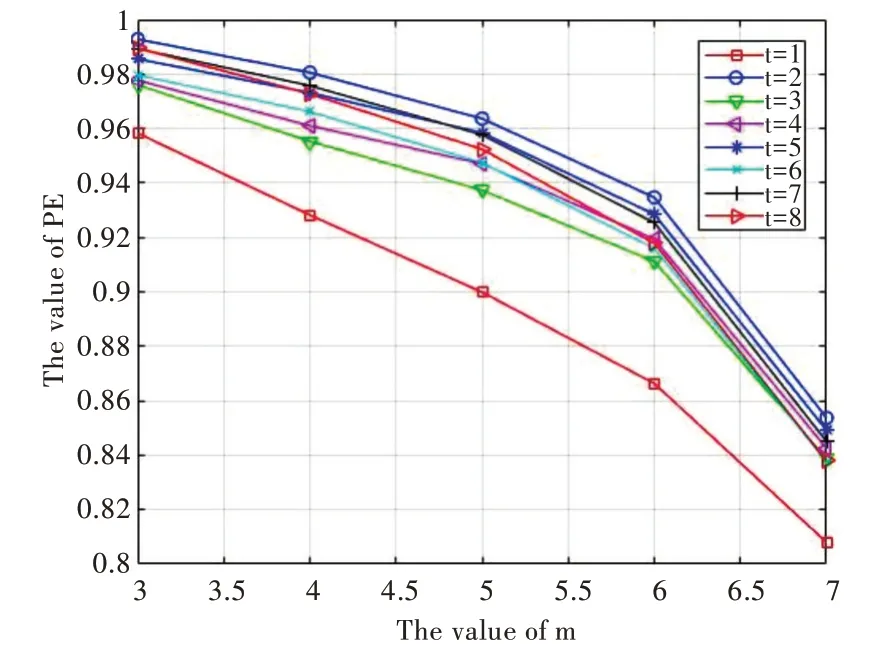
Fig.2 The curve of time delay t and sleep EEG PE value图2 时间延迟t 与睡眠脑电PE 值变化曲线

3.2 多尺度排列熵算法参数设计优化

为了避免排列熵在实际应用过程中可能存在过于敏感的现象，并增加算法的稳定性和可移植性［18］，在排列熵基础上通过引入信号的粗粒化操作，提出多尺度排列熵的概念。MPE 方法包括两个步骤：信号粗粒化、计算每个时间序列PE 值。算法具体步骤如下［19］：

（1）原始数据分类。根据hyp 文件里标签的不同将数据分成5 类：W 期数据、N1 期数据、N2 期数据、N3 期数据、REM 期数据。

（2）构建连续的粗粒化时间序列Z(t)(j)，其中j为粗粒化过程中的取值范围，1 ≤j≤N/t。

（3）对长度为t 的非重叠窗口数据点求平均，完成信号粗粒化，计算公式如式（4）所示。

式中，t 代表尺度因子，取值范围为t=1,2,...,N。当t取1 时，时间列Z(t)(j) 即为原始信号；当t＞1 时，每个粗粒化时间序列长度为。

（4）构造一个pec 函数，function［PE］=pec（y，m，t），完成熵值计算，其中y 为粗粒化后的时间序列，m 为嵌入维数，t 为时间延迟。

要探究基于多尺度排列熵的睡眠脑电阶段阈值范围，首先要选取合适的嵌入维数m。嵌入维数m 反映时间序列相空间重构过程中所取信号片段长度，m 值越大，所取片段越长；m 值越小，所取片段越短。若m 值过小，相空间重构后的k 个重构向量信息量太少；若m 值过大，该k 个重构向量的符号序列会过于平均，使得排列熵值不能很好地表征信号特征［20］，因此需探究嵌入维数m 对睡眠脑电PE值计算的影响。

以某一受试者W 期样本信号为例，尺度因子选取1～15，时间延迟取2，嵌入维数m 分别取4、5、6、7，不同嵌入维数与多尺度排列熵值变化曲线如图3 所示（彩图扫OSID码可见）。从图中可以看出，4 条曲线变化情况均呈整体波动下降趋势，MPE 熵值随嵌入维数m 的增大而降低。与较小的m 值相比，较大的m 值计算的多尺度排列熵值曲线斜率明显增加，说明较大的m 值更为敏感。与时间延迟一样，嵌入维数m 值与计算时间呈正相关。对于较长的EEG信号而言，较小的m 值将导致算法无法准确运行，较大的m 值是优选，因此本研究嵌入维数m 取6 较为合适。

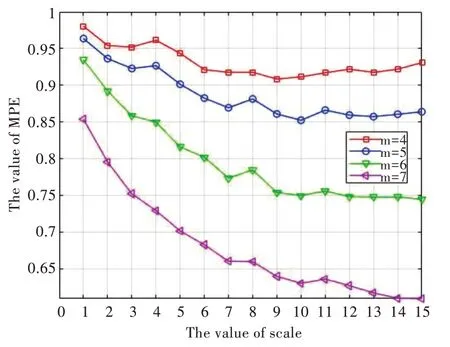
Fig.3 The curve of embedding dimension m and MPE value图3 嵌入维数m 与MPE 值变化曲线

在进行睡眠脑电MPE 熵值计算过程中，过小的尺度因子会造成睡眠脑电信号粗粒化程度不够，导致无法全面提取W 期、N1 期、N2 期、N3 期和REM 期特征熵值，使得阈值范围不准确，但过大的尺度因子会使熵值易受粗粒化序列长度的影响。取嵌入维数为6，时间延迟为2，多尺度因子为1～15，五期睡眠阶段不同的多尺度因子与MPE 值变化曲线如图4 所示（彩图扫OSID 码可见）。

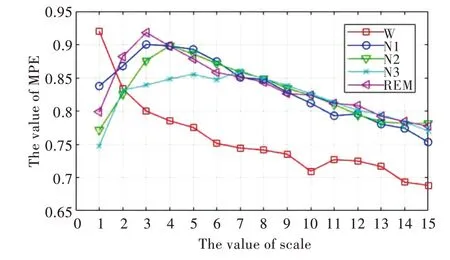
Fig.4 Multi-scale permutation entropy curve of EEG signals in the five stages of sleep图4 五期睡眠阶段脑电信号多尺度排列熵曲线

从图4 可以看出，W 期脑电信号与尺度因子呈负相关，而另外四期脑电信号随着尺度因子的增加会先升高再降低，同一尺度因子在不同睡眠阶段下计算出的熵值存在较明显的差异，说明将MPE 熵值作为睡眠脑电分期特征向量的方案可行。当尺度因子为1 时，除W 期熵值较高外，其余四期熵值偏低，说明此时获取的信息完整度不高。当尺度因子大于3 时，一方面N1 期、N2 期、N3 期和REM 期熵值开始出现重叠，使得计算出来的多尺度排列熵值无法作为特征值表征睡眠各期，另一方面过大的尺度因子会造成不必要的计算量，影响计算效率，故不可取。当尺度因子在1～3 之间时，MPE 熵值增加说明较小的尺度因子对熵值计算更为敏感，而当尺度因子为3 时，N1 期和REM 期取得最大熵值，除W 期外，其余四期所得熵值均偏大，5 种状态下的睡眠脑电所得熵值可以得到较好区分，MPE 对于分析W 期、N1 期、N2 期、N3 期和REM 期的EEG 信号具有较好的鲁棒性。因此，当尺度因子为3 时可得到最优解，此时睡眠各期的熵值从大到小排序为REM 期、N1 期、N2 期、N3 期和W 期。

4 睡眠阶段阈值范围讨论

为避免单一样本存在的偶然性和数据的不平衡性，本文从Sleep-EDF 数据集中选取4 组实测数据作为研究对象，其中两组数据sc4002e0、sc4012e0 为睡眠健康受试者数据，另外两组数据st7022j0、st7052j0 为入睡困难受试者数据，将4 组实测数据分别标号为1、2、3、4。

设置多尺度排列熵参数如下：嵌入维数为6，时间延迟为2，多尺度因子为3。为探究基于MPE 值的睡眠各期阈值范围，将上述4 组数据经预处理后分别采用多尺度排列熵算法计算各期熵值。研究结果显示，REM 期的熵均值最大，在0.85～0.90 之间，N3 期的熵均值最小，在0.80～0.85之间。睡眠五期熵值按从大到小排序为REM＞N1＞N2＞W＞N3，说明可将MPE 熵值作为评价睡眠各期阈值范围的标准之一。

为了进一步直观反映W 期、N1 期、N2 期、N3 期和REM 期的阈值范围，不同分期的多尺度排列熵均值分布情况如图5 所示（彩图扫描OSID 码可见）。

Fig.5 Distribution of entropy of multi-scale arrangement in each stage of sleep图5 睡眠各期多尺度排列熵分布情况

从图5 可以看出，N1 期和N2 期之间阈值范围在0.84～0.90 之间，差异较小；REM 期的多尺度排列熵阈值范围最大（MPE＞0.86），中间值约在0.88～0.89 之间，与N1 期、N2 期存在一定差异，但这种差异没有N3 期、REM 期和W期明显，这是因REM 期的大脑开始有了一定思维活动造成的；N3 期的阈值范围最小（0.78＜MPE＜0.86），中间值约在0.80 左右；W 期的阈值范围在0.80～0.90 之间，中间值约在0.84 左右。

截至目前，针对基于非线性方法的睡眠EEG 信号阈值研究还较少，如刘欣［21］基于近似熵的脑电特征提取方法对睡眠EEG 信号进行分析，发现处于不同睡眠阶段所对应的近似熵值也不同，REM 期的熵值与N1 期和N2 期较为接近，从图6 中也可以得出相同结论，这是由于REM 期开始出现一定思维活动造成的；Shao 等［22］基于EMD 和多尺度模糊熵的脑电特征提取方法对睡眠EEG 数据进行计算与处理，以计算出的多尺度模糊熵值作为睡眠阈值的度量，发现当尺度因子为2 时，多尺度模糊熵得到最大值，此时W 期的阈值范围在4.5～6.5 之间，N3 期的阈值范围在3～4 之间，N1 期和REM 期的阈值范围差异不明显。在本文所得结论中，N1 期的阈值范围比REM 期小，N1 期的中位数低于0.88，而REM 期的中位数高于0.88。通过对比发现，多尺度排列熵算法可提高N1 期与REM 期之间的差异性，证明该算法在提高N1 期与REM 期之间的阈值分辨率上是有效的。

5 总结与展望

非线性分析方法在人脑电图中的应用仍处于试验阶段，尚未广泛应用于临床疾病的早期诊断［23］，但基于非线性动力学的方法在睡眠相关领域研究中存在巨大潜力。本文通过使用MPE 非线性动力学方法对比分析不同时间延迟、不同嵌入维数和不同多尺度因子对熵值的影响，在睡眠阶段脑电分期研究中，MPE 算法的最优时间延迟为2，最优嵌入维数为6，最优尺度因子为3。

本文以MPE 熵值作为评价标准研究睡眠阶段阈值范围，结果发现REM 期的阈值范围最大（MPE＞0.86），N3 期的阈值范围最小（0.78＜MPE＜0.86），W 期的阈值范围在0.80～0.90 之间，N1 期和N2 期之间的差异不太明显。通过与相关文献对比分析发现，MPE 熵值可提高REM 期与N1 期的阈值分辨率，从而较好地区分睡眠各期。本研究为探索睡眠障碍脑电信号提供了一种新方法，在未来工作中可增加诱发脑电的刺激种类，通过融合多种生理信号以提高睡眠分期的阈值分辨率。