PSO 优化算法在平滑路径规划中的应用

周钊扬，穆平安，张仁杰

（上海理工大学光电信息与计算机工程学院，上海 200093）

0 引言

路径规划（Path Planning）是指运用所编制的算法使目标在障碍环境中，根据任务要求和评判准则自行找到并规划从起点至目标点的最优路径［1］。随着相关智能技术的一系列突破和发展，其在军事、医疗等高新科技领域都已得到了广泛应用［2］，在未来也有着广阔的发展前景。

研究者们又将路径规划算法与移动机器人相结合，主要涉及到的智能算法有：模拟退火算法、人工鱼群算法、粒子群算法等［3］，以更好地解决障碍环境下移动过程中的路径规划问题。其中，粒子群（PSO）算法有着结构简单、通用性强、在迭代过程中搜索效率更高等优点［4］，但同时也存在着缺乏对速度的动态调节、收敛精度低、搜索停滞等不足［5］，这对于路径规划效率和准确度都会产生一定影响。

实际应用中的粒子群算法大多先通过随机解来初始化粒子，再在反复迭代过程中寻找最优方案，而忽略了路径是否平滑等指标［6］，这将导致只有最优粒子参与其中，且规划产生的路线较依赖于直角坐标系环境［7］。当环境为球面坐标或极坐标时，PSO 算法则常生成多折角相连的不平滑路径，从而造成机器人功耗加大及效率降低［8］。通过综合考量，对机器人行进路径的平滑度进行优化是眼下粒子群算法改进的重要方向之一。

本文针对上述问题，提出一种改进的自适应粒子群算法，并结合贝塞尔曲线［9］以提高机器人寻找最优路径的平滑度和效率。为了更快找到局部最优解并避免收敛缓慢的问题，在ES-PSO 中采用较大的控制参数值以平衡惯性权重，进而提高粒子的有效性。此外，通过带有罚函数的适应值函数优化策略，使机器人可以更快速、准确地得到全局最优路径，且优化过后的平滑路径更适合移动机器人行进。

1 粒子群算法优化

1.1 算法基本原理

PSO 算法始于对鸟类捕食状态的研究，其使N维搜索区域中的每个粒子都具有表示位置的xi和表示速度的vi两个矢量［10］。每次迭代时，粒子都将学习自身的历史最佳位置并与群体交换，从而对信息进行搜索与更新［11］。令分别为第i个粒子的速度矢量和位置矢量，M为种群中的粒子数量。在标准PSO 算法中，可通过以下公式对粒子的两个矢量进行更新：

速度向量更新的数学模型为：

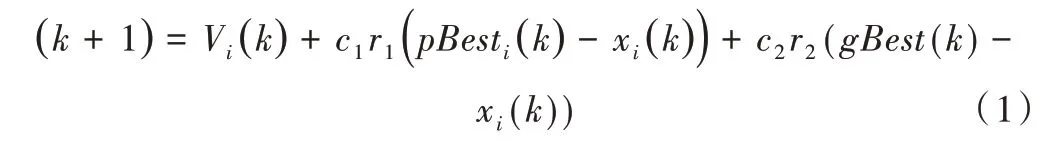
位置向量更新的数学模型为：

式中，pBesti是粒子i(i=1,2,…,M)历史上的最佳位置，gBest(gBest1,gBest2,…,gBestn)是整个群体历史上的最佳位置，k为当前迭代次数，c1、c2为学习因子，分别是衡量pBesti和gBest相对重要性的两个参数，r1、r2则为［0，1］区间内的随机数。

式（1）中的Vi(k)为“自身记忆项”，表示粒子由于自身惯性，将向前一次迭代的方向移动；c1r1(pBesti(k) -xi(k))为“自身认知项”，表示粒子会向着历史最佳位置处移动，代表了粒子自我学习的能力；c2r2(gBest(k) -xi(k))为“群体认知项”，表示粒子向种群最佳位置处移动的能力［12］。因此，其整体可视作粒子在解空间内不断移动以寻找最优解的过程。

在每次迭代中，每个粒子自身所在位置都对应一个适应度值f：

其中，f(xi)为算法实际需要求解的函数。

1.2 PSO 优化算法

针对粒子群算法在二维场景下缺乏对速度的动态调节以及容易出现局部最优等局限性［13］，提出一种自适应粒子群算法，该算法对种群进化状态评估、自适应惯性权重选择和抑制最优值区域扰动3 个方面进行了优化。

1.2.1 种群进化状态评估

传统PSO 算法是根据种群中心位置计算进化因子，而对种群的进化状态往往考虑欠佳。这将导致当两个距离较近的粒子开始进化时，若其速度矢量差别较大，则迭代后的位置可能相距较远［14］。因此，针对这种评估方法存在的问题，本文提出改进的种群进化状态判断方法。

设f(gBest(k))表示第k代时种群中最佳粒子的适应值，因此在全部迭代中，{f(gBest(0)),f(gBest(1)),…,f(gBest(k))}是一个非升序列，即：

设f(pBesti(k))表示第k代时粒子i的历史最佳位置适应值，则对于每个粒子，{f(pBesti(0)),f(pBesti(1)),…,f(pBesti(k))}也是一个非升序列，即：

因此，全部pBesti(i=1,2,…,M)的适应值之和满足：

在3 个序列中，δgBest(k)、δpBesti(k)和(k)依次为全局最佳粒子改进、单个粒子历史最佳位置改进以及集体历史最佳位置改进，由此改进可以有效地对种群进化状态进行更实际的判断。

1.2.2 自适应惯性权重选择

惯性权重在PSO 算法中起着调整局部搜索和全局搜索的重要作用，通常呈递减状态变化。但合理的惯性权重需同时考量搜索空间维度、当前搜索状态、种群大小等多种因素才能提高搜索效率，避免粒子惯性分量造成的不利影响［15］。因此，为了同时提高收敛精度和效率，本文针对惯性权重的特点为学习因子设计一个自适应控制器。

学习因子包括c1和c2。c1通过自我学习使自身找到历史最佳位置，有助于搜索新区域；c2则帮助粒子群提高全局搜索能力，加快收敛速度。在不同的种群进化状态下，具体策略如下：

（1）当处于探索状态时，应探索尽可能多的最优值，提高模型求得最优解的能力。此时，为提高粒子搜索速度并进行精细化搜索，应增加c1值并减少c2值，避免其趋向于局部最优。

（2）当处于收敛状态时，理论上应增加c2值并减少c1值，使粒子群朝全局最优位置移动。但由多次实验结果来看，这种策略会加快参数变化，不利于平衡搜索能力和收敛速度。因此，此时应增大c1和c2值。

（3）当处于困死状态时，应尽量使群体脱离当前全局最优。此时应减少c1值并增加c2值，从而促使粒子跳离困死状态，在其它位置再次生成全局最优。

综上所述，本文设计的自适应控制器决策树如图1 所示。

基于该决策树，并通过大量实验尝试，将学习因子c1和c2初始化为2.0。实验结果表明，动态自适应学习系数可使系统寻找到更好的全局最优点。

1.2.3 抑制最优值区域扰动

当处于困死状态时，粒子均困在当前全局最佳区域，应尽快使粒子脱离该状态，向更优区域移动［16］。因此，本文设计了一种跳出局部最优的策略，可以改善传统策略成功率及效率较低的缺点。具体策略如下：

式中，Xmax、Xmin依次表示搜索区域上限和下限，j为粒子维度。当粒子跳出但并未寻至更优区域时，将种群还原回之前的状态并在下一代时重新跳出，直至进化状态得到优化。大量实验结果表明，该策略可以更高效地跳出当前全局最佳区域，抑制最优区域的扰动，寻找到更精确的最优值。

Fig.1 Adaptive controller decision tree图1 自适应控制器决策树

1.3 算法流程

算法具体流程如下：

步骤1：对种群中的粒子位置与速度等参数进行初始化，令迭代次数k=0。

步骤2：计算各粒子的适应度值。

步骤3：根据式（1）所示模型对速度向量进行更新。

步骤4：根据式（2）所示模型对位置向量进行更新。

步骤5：按式（8）计算上一次迭代后的适应度值，根据适应度更新粒子的历史最佳位置。

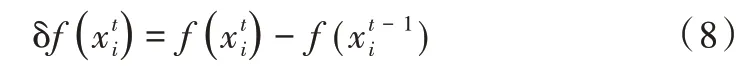
步骤6：计算δgBest(k)、δpBesti(k)和(k)，并评估种群进化状态。

步骤7：根据评估结果，更新当前条件下的惯性权重ω以及学习因子c1、c2。

步骤8：判断收敛情况，若种群处于困死状态，执行步骤9；若非困死状态，跳至步骤10。

步骤9：依照式（7）执行跳出策略。

步骤10：判断终止情况，若满足条件，则算法结束；若不满足，跳回步骤2。

2 路径平滑度优化

通过传统PSO 算法规划出的路径常常存在转弯折线多、路径不够平滑、对机器人耗损大等问题，因此路径规划研究具有重要的理论意义与实际价值［17］。其不仅能提高机器人行进过程中的灵活性，而且是机器人完成其他任务的先决条件。本次研究将通过ES-PSO 算法求解出的路径节点与Bezier 曲线相结合，以提高机器人移动的平滑度。

Bezier 曲线是一种参数曲线，是由伯恩斯坦多项式发展演化而来的，因其具有独特的控制方式和对曲线强大的拟合能力，被大量应用于工业领域［18］。在组成它的众多控制点中，只有起始点和终点在曲线上，其它点均不在曲线上。曲线表示方法如下：

设一组控制点向量为P0,P1,…,Pn，则Bezier 曲线可表示为：

其中，t是归一化的时间变量，Pi=(xi,yi)T代表第i个控制点的坐标向量，xi、yi分别为X和Y的坐标分量，Bni(t)为Bernstein 多项式：

在二维平面上，Bezier 曲线的曲率可表示为：

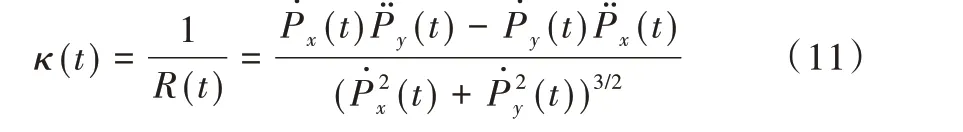
其中，R(t)为曲率半径为Bezier 曲线P(t)对x 和y 的一阶、二阶导数。

Bezier 曲线的平滑度与路径的曲率函数息息相关，接下来将融合Bezier 曲线与ES-PSO 算法对机器人路径规划进行仿真。

3 路径规划相关描述与建模

3.1 路径初始化

传统PSO 算法的路径初始化策略往往会规划出不必要的路线和曲折的拐弯，但这样的路径并非最优路径，且会增加算法花费的时间和机器人损耗［19］。因此，本文为路径初始化策略提供了新思路，以期在路径初始化阶段即得到更好的规划效果。

将路径起点与终点之间的线段看作线段D。在连线D上除起点和目标点外，取维度N-2 个点，则所有点的坐标都可记作：

从每一点作连线D的垂线，标记为l1,l2,…,lN-2。在l1,l2,…,lN-2上任意各取一点，标记为p2,p3,…,pN-1。从起点按顺序连接p2,p3,…,pN-1等所有点。

根据该方案规划出的路径可以消解多余的曲折，更贴近机器人实际的最佳运动轨迹。如果路线穿过障碍物，则需要对其进行排除。将根据此方案及其它方案初始化得到的初始路径进行对比，如图2 所示。其中，紫色路径为起始点至目标点间的最短距离，绿色路径为随机初始化的初始路径，红色路径为根据本文策略初始化的初始路径。

由图2 可知，基于传统PSO 算法路径初始化策略规划的路线往往具有随机性，会对接下来机器人行进造成一定影响。而采用本文策略进行初始化，则能更好地得到接近最优的初始路径，很大程度上避免了机器人在折线上的能量损耗，并节约了时间成本。

Fig.2 Initial path under different initialization strategies图2 不同初始化策略下的初始路径

3.2 结合罚函数定义适应值函数

适应值函数的选用对提高收敛精度和速度来说至关重要，而机器人行进过程中的安全保障也应作为必要因素考虑进路径规划中。在常规的PSO 算法中，往往选取路径长度函数对适应值函数进行定义，具体如下：

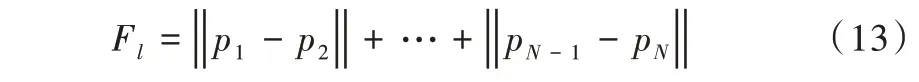
式中，Dob表示障碍存在区域，在此设罚函数为200。设Dsa为保护区域，路径穿过此区域时罚函数会变大，余外区域的罚函数都为0。d表示粒子至障碍物中心的长度，rob表示障碍存在区域的半径，rsa表示保护区域的半径。则由本文障碍物的环境地图映射得到罚函数地图，如图3 所示。

将上述两个函数相结合，重新定义适应值函数如下：

其中，a、b依次为长度函数权重与罚函数权重，本文均取值为0.5。

4 仿真与分析

基于MATLAB 建立仿真平台，在相同设定下对本文提出的改进ES-PSO 算法与传统PSO 算法作仿真测试和对比分析，并证明了本文初始化策略的可行性。

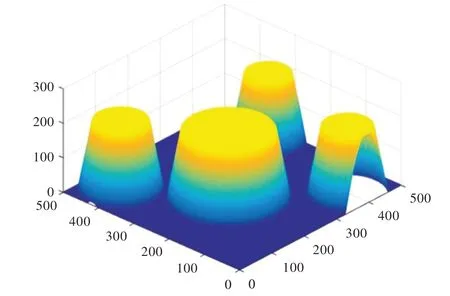
Fig.3 Penalty function map图3 罚函数地图

4.1 初始化策略效果

设机器人运动的起点坐标为[50,50]，终点坐标为[450,450]。根据本文提出的自适应粒子群ES-PSO 算法进行路径规划，折线为粒子群算法规划出的路径，曲线为结合Bezier 曲线生成的平滑路径，比较有初始化策略和无初始化策略时算法寻优精度与寻优速度的差异。

设算法种群粒子数量M为30，路径节点N为5，迭代200 次，限制粒子速度范围为[-50,50]。惯性权重ω=[0.9,0.4]，设学习因子c1和c2的初始值为2.0。ω、c1和c23个参数则通过算法迭代过程中种群进化状态的变化实现自适应控制。

如图4 所示，实线和虚线分别表示采用初始化策略和无初始化策略时的适应值变化曲线对比。

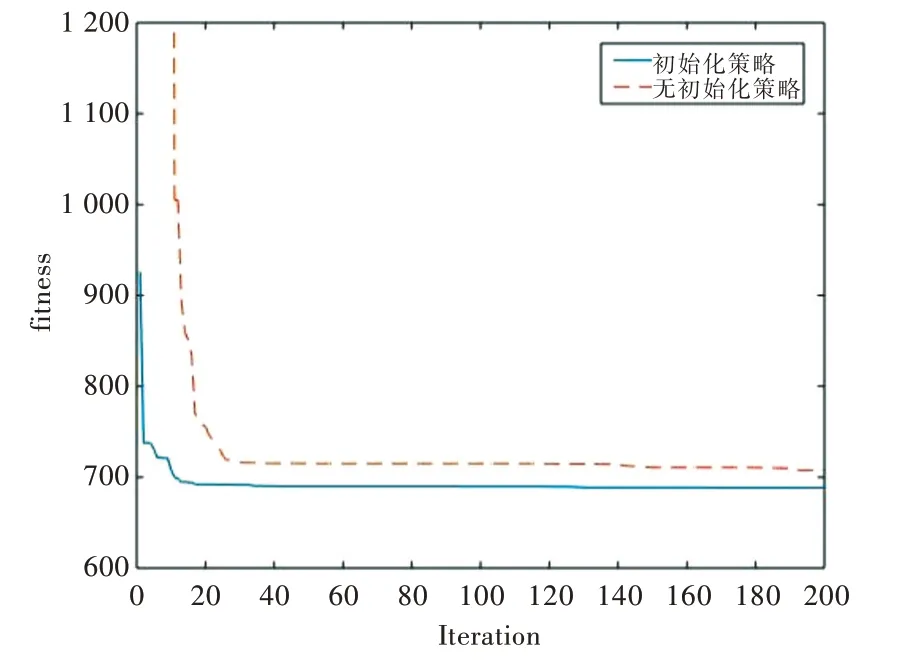
Fig.4 Initialization strategy fitness value change curve comparison图4 初始化策略适应值变化曲线对比

由图4 可得，二者虽变化趋势相同，但采用初始化策略后的曲线在另一曲线下方，且更早趋于平缓，表示采用初始化策略有效提高了PSO 算法的寻优能力和运算效率。

为了提高测试准确度，采用两种方式重复进行100 次测试，得到平均适应值函数Fitness、平均迭代次数Iteration和路径规划成功率Success，如表1 所示。由表可知，执行初始化策略后的路径规划成功率更高，表明初始化策略可增强路径规划的成功率。

Table 1 Initialization policy effects表1 初始化策略效果

4.2 算法寻优性能比较

分别在简单和复杂环境下比较PSO 算法、GPSO 算法、APSO 算法及本文提出的改进ES-PSO 算法的寻优性能。设定4 个规则的圆形障碍区域为简单测试环境，图5、图6（彩图扫OSID 码可见，下同）分别为简单测试环境下4 种粒子群算法的路径规划结果与适应值变化曲线。其中，蓝色曲线表示PSO 算法，红色曲线表示GPSO 算法，黄色曲线表示APSO 算法，紫色曲线表示ES-PSO 算法。

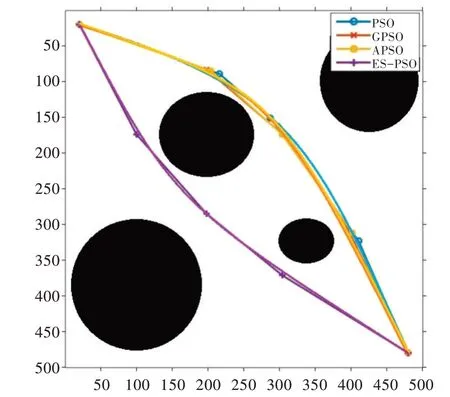
Fig.5 Planning path results in a simple environment图5 简单环境下路径规划结果

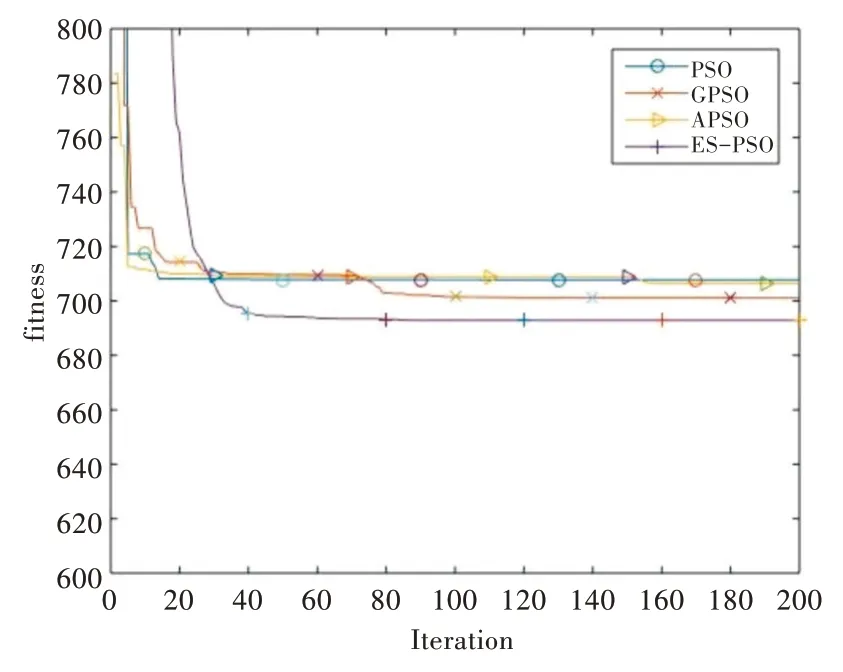
Fig.6 Adaptive value curve in a simple environment图6 简单环境下适应值变化曲线

由图5 可知，4 种算法均可规划出规避障碍的有效路径，但ES-PSO 算法能够跳出局部最优，得到更佳路径。在该环境下重复测试100 次，实验结果如表2 所示。

由表2 可知，PSO 算法在4 种方法中收敛速度最快，但易陷入局部最优，成功率较低。而ES-PSO 算法在明显提高寻优效率和保证收敛速度的同时，规划正确率也维持在一个较高水平。

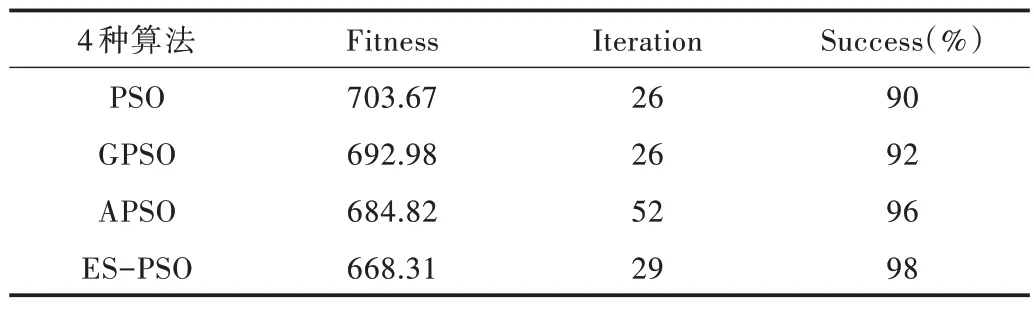
Table 2 Simple environment path planning表2 简单环境路径规划

设定大量障碍物，且障碍物形状不仅局限于圆形的复杂测试环境，如图7 所示。图7、图8 分别为复杂测试环境下4 种粒子群算法的路径规划结果与适应值变化曲线。

Fig.7 Path planning results in a complex environment图7 复杂环境下路径规划结果

Fig.8 Adaptation value curve in complex environment图8 复杂环境下适应值变化曲线

在该复杂环境下重复测试100 次，实验数据如表3 所示。

Table 3 Complex environment path planning表3 复杂环境路径规划

由表3 可知，当障碍物变得复杂及不规则时，PSO 算法和GPSO 算法都过早进入收敛且成功率有所降低。APSO算法规划的结果虽维持了精度和成功率，但收敛效率较低。而本文的ES-PSO 算法在效率、寻优精度、成功率3 个指标上均表现良好，相比其它算法的规划结果展示出显著的改进效果。

5 结语

围绕移动机器人如何规划出一条从起始点到目标点的无碰撞最优路径这一关键问题，本文分析了传统算法存在的不足，提出一种基于种群进化状态的自适应粒子群算法（ES-PSO），从种群动态进化状态判定、自适应控制惯性权重调整、跳出策略选择几方面对算法进行优化，提出初始化路径策略和带有罚函数的适应值函数策略，并引入贝塞尔曲线以提升路径平滑度。在简单环境和复杂环境下将改进后的算法与传统算法进行仿真比较，结果均表明改进后的算法在测试中成功率较高，能够在保留标准PSO 算法优点的同时，更加迅速地得到平滑路径，符合实际需要，具有一定研究价值。另外，如何在动态环境下对粒子群算法的监测及判断能力等进行改进，以及对三维空间中移动机器人的路径规划进行建模等问题，有待后续进一步研究。