基于藤Copula的HAR模型扩展

杨涛 付英姿 李薛莎

摘要：波动率可以衡量金融市场风险，在资产配置和风险管理等方面有重要意义。文章在基于高频交易数据的HAR模型上对其进行修正，利用藤Copula对HAR模型涉及的四个波动率成分联合建模（CV-HAR模型），并基于历史数据的条件期望提取波动率预测值。实证分析以上证交易所的20支股票作为研究样本，对CV-HAR模型和历史模型（HAR）性能进行评估，结果表明，CV-HAR模型克服传统模型线性结构限制，并充分描述了联合分布依赖关系，在对未来波动率的预测行为方面更加精准。

关键词：波动率;藤Copula;HAR模型

一、引言

金融资产波动率的估计与预测是金融计量经济学的主要研究领域。自Andersen和Bollerslev（1998）首次利用高频交易数据提出的已实现波动率（RV）以来，高频数据成为研究波动率的重要手段。随后Corsi（2004，2009）根据异质市场假说理论，将市场波动划分为三种波动形式（短期波动、中期波动和长期波动），提出了异质自回归已实现波动率模型（HAR-RV），其实证结果表明该模型的预测能力明显优于GARCH和ARFIMA-RV等波动率预测模型。与此同时，许多学者在HAR族模型基础上构建新的预测模型，提高模型对市场波动率的预测能力。

HAR族模型最大的一个特点就是线性，受特定的回归形式所限制，这使得模型在预测方面没有很好的应用。一般回归问题的表达式为RV=f（X，β）=IE[RV|X]，其中X是回归向量，β是参数向量。本文的工作是直接利用条件分布函数FRV|X计算得到IE[RV|X]，其中条件分布函数可由联合分布FRV，X获得。该方法并没限制回归函数的特定形式，而是通过联合分布函数来确定函数变量间相关关系。Copula（Nelsen，2000）将复杂的联合分布拆分为单变量的边缘分布和变量间的相关结构来独立研究，能够更加灵活地描述变量间复杂依赖关系。Sokolinskiy和van Dijk（2011）提出了一种基于Copula的已实现波动率（RV）估计方法和预测方法，实证分析表明Copula可以灵活而简洁地捕捉波动率相关特征，在预测方面的准确性和效率都由于传统预测方法（HAR模型）。而本文主要是对HAR模型进行修正，即对三种不同的波动率成分使用Copula函数进行联合建模。在选取Copula函数时，本文采用了更为灵活地藤Copula（Joe，1996）来描述多个变量间的相关关系。藤Copula把多元联合密度函数分解为条件边缘分布密度函数和一系列Pair-Copula的乘积。

因此，本文利用藤Copula在HAR模型上对回归函数进行一般化，通过条件分布函数确定（简称CV-HAR模型）。在实证分析中，本文考虑了2015～2019年上证交易所20支股票的高频交易数据，并采用不同的估计和预测方案来评估本文模型与HAR模型。

二、理论

（一）HAR模型

1. 已实现核（Realized Kernel，RK）波动率

令pt表示t时刻的对数资产价格，假设每日有M个观测值，为{p1，…，pi，…，pM}，则每日已实现波动率（RV）为：

Barndorff-Nielsen（2008）提出的已实现核（RK）波动是一种新的波动率非参数估计方法，该方法在最优时间窗口构造RV的核密度估计式。RK能有效滤出噪音更贴近于真实波动率，其估计形式如下：

其中，γh为自协方差过程，wh=（w-H，…，w-1，w0，w1，…，wH）′是核加权函数。

2. HAR-RK模型

HAR模型的理论基础是异质市场假说，将异质市场中的交易者分为短期交易者、中期交易者和长期交易者，分别表现为昨日已实现核波动率（RK）、周已实现核波动率（RK）和月已实现核波动率（RK）。则HAR-RK模型可表示为：

其中RK是今日已实现核波动率，β0是截距项，β（d）、β（w）和β（m）分别表示周以及月已实现核波动率的回归系数，εt是具有独立性和零均值特点。

（二）CV-HAR模型

HAR模型中实质上是RK滞后项的线性组合，该模型存在着模型结构固化和无法描述非线性特征的缺陷。本文研究RK，RK，RK，RK的联合分布F，并通过提取条件分布F得到RK的条件期望：

式中εt为随机误差项。该模型可以作为式（3）的一般化，HAR模型的f是线性函数，而本文讨论的模型是无固定结构的条件期望形式。因此，本文利用藤Copula对四种波动率的联合分布进行建模，该方法在多变量联合建模方面优势尤为突出。

1. CV-HAR定义

由于四种波动率（RK，RK，RK，RK）的特殊性，本文使用C藤Copula对这四种波动率进行建模（简称CV-HAR）。C藤是所有藤中最常见的一个子类，具有典型的“星型”结构，其中每棵树都有一个唯一的节点连接其他所有节点。假设d有个变量（X1，X2，…，Xd），F表示分布函数，f表示密度函数，则C藤的密度函数有如下分解式：

关于C藤结构的确定，通过变量间的相关关系简化其选择问题，使其结构更有解释性。本文四种波动率在时间方面是存在特殊关系的，由于月已实现核波动率（RK）驱动着其他三种波动率，因此将RK作为C藤中第一棵树的中心节点。同理，考虑四种波动率中当前波动率会受到历史波动率的影响，可得到C藤的结构图如下。

其中，第一棵树所有的依赖关系都是是RK与其他波动率之间的，最后一个树中描述在周和月的已实现核波动率条件下今日和昨日波动率（RK和RK）之間的关系。

2. CV-HAR模型估计与条件期望

关于CV-HAR模型的估计，本文采用边际推断函数法（IFM）：

（1）估计四种波动率的边际分布函数。本文采用以下方法进行估计：参数估计（偏t分布）;核密度估计;经验分布函数估计（ECDF）。

（2）藤结构的确定。由于变量特殊性，C藤呈现一个特殊的结构图（见图1）。

（3）利用信息准则（AIC或则BIC）对所有双变量Copula进行选择。其中存在类似C23|1的双变量Copula包含条件分布函数F3|1和F2|1，可以通过下式求得：

其中v是m维向量，vj是v的任意分量，v-j是v从中除去vj的m-1维向量，C（·，·）是双变量Copula函数。

（4）利用式（11）可得基于C藤结构的多元变量联合分布。

对于评估条件期望IE[X|v]的首要条件是计算条件分布函数，而条件分布函数可以通过藤分解递归地求出见式（6）。

三、实证分析

（一）数据描述

为体现出CV-HAR模型性能的一般性特征，本文随机挑选了上海证券交易所中20支股票的5分钟高频交易数据作为研究样本。数据来源于微盛投资（http：//www.wstock.net/），样本的跨度为2015年1月至2019年12月，共计1219天。由于需要计算今日已实现核波动率（RK）、昨日已实现核波动率（RK）、周已实现核波动率（RK）和月已实现核波动率（RK），数据需要从第23天开始截断，因此观测数据一共1197个。

（二）估计和预测方案

本文在三种不同的方案下，分别对HAR模型和CV-HAR模型进行估计，并制定相应的预测措施。

1. 固定窗口（Fixed Window，FW）

将分别使用W={500，750，1000}个观测值进行模型估计。第1天到第W天的观测部分用于样本内分析，其余W+1天到最后一天用于样本外分析。

2. 增加窗口（Increasing Window，IW）

首先估计1到初始值W0天的HAR模型和CV-HAR模型，然后依次改变W=W0+i，i=1，…，1191-1-W0，并重新对1到W天进行估计，每次估计都进行一次提前一步预测（即预测W+1天）。初始值W0={500，750，1000}。

3. 滚动窗口（Rolling Window，RW）

类似于增加窗口（IW），不同的是估计的时间窗口是滚动变化。初始值为W0={500，750，1000}，对W-W0到W天进行模型估计，并预测W+1天的波动率值。

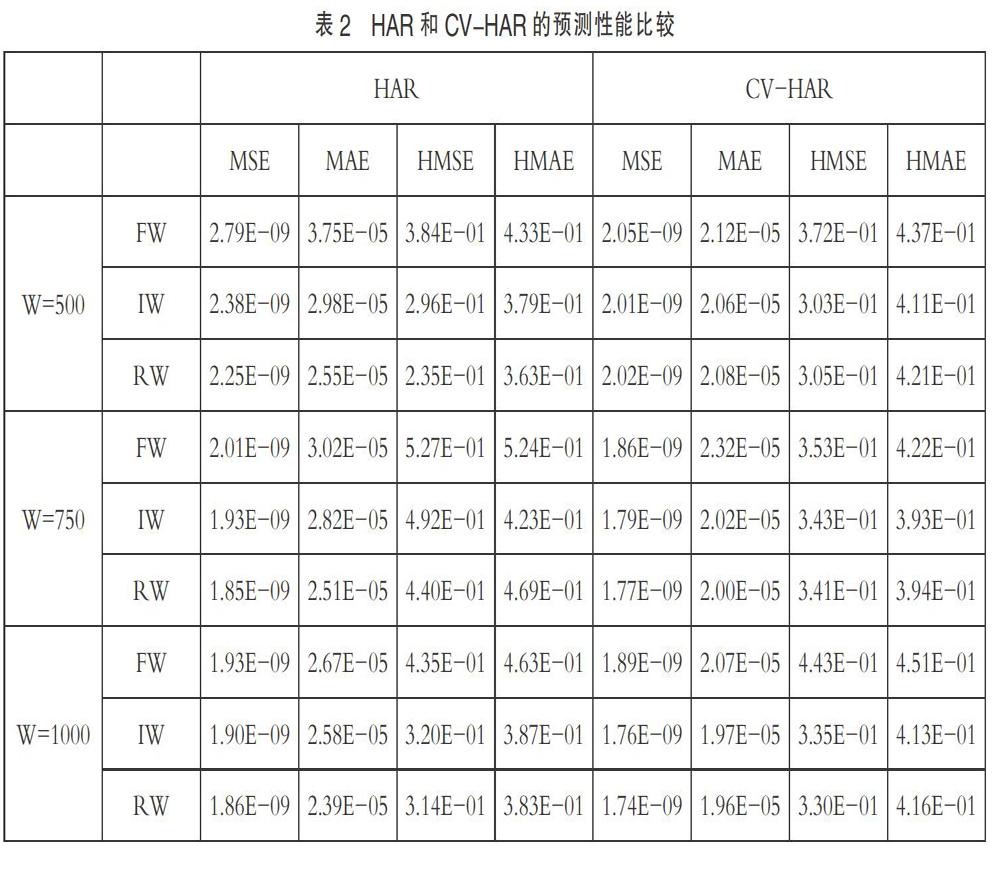
本文选取四种常见的损失函数来评价HAR和CV-HAR模型的性能：均方误差（MSE）、平均绝对误差（MAE）、异质调整均方误差（HMSE）和异质调整平均绝对误差（HMAE）。

（三）结果分析

首先，利用固定窗口对HAR模型和CV-HAR模型进行估计。表1的结果显示，固定窗口的大小对模型的结果有重要的影响，随着窗口的扩大，四种损失函数都有着显著的改善。将模型结果分为样本内和样本外分析，可以看出呈现的结果有明显的区别。样本内的结果显示HAR模型总体上表现出更好的性能，而样本外的结果显示CV-HAR模型都有着明显的优势。HAR模型在样本内有着很好的拟合效果，但不能应用于对未来的预测，然而CV-HAR模型利用藤Copula的灵活性，充分描述了波动率之间的依赖关系，对未来的预测提供了更可靠结果。此外，在拟合CV-HAR模型的三种边际拟合函数中，经验分布函数拟合效果最佳，经验分布函数估计不受模型的限制，很好地刻画了波动率的分布。图2给出了关于HAR模型和CV-HAR模型的样本外预测图，图中HAR模型的预测值整体上高估了RK值，而CV-HAR模型更加接近真实的值。

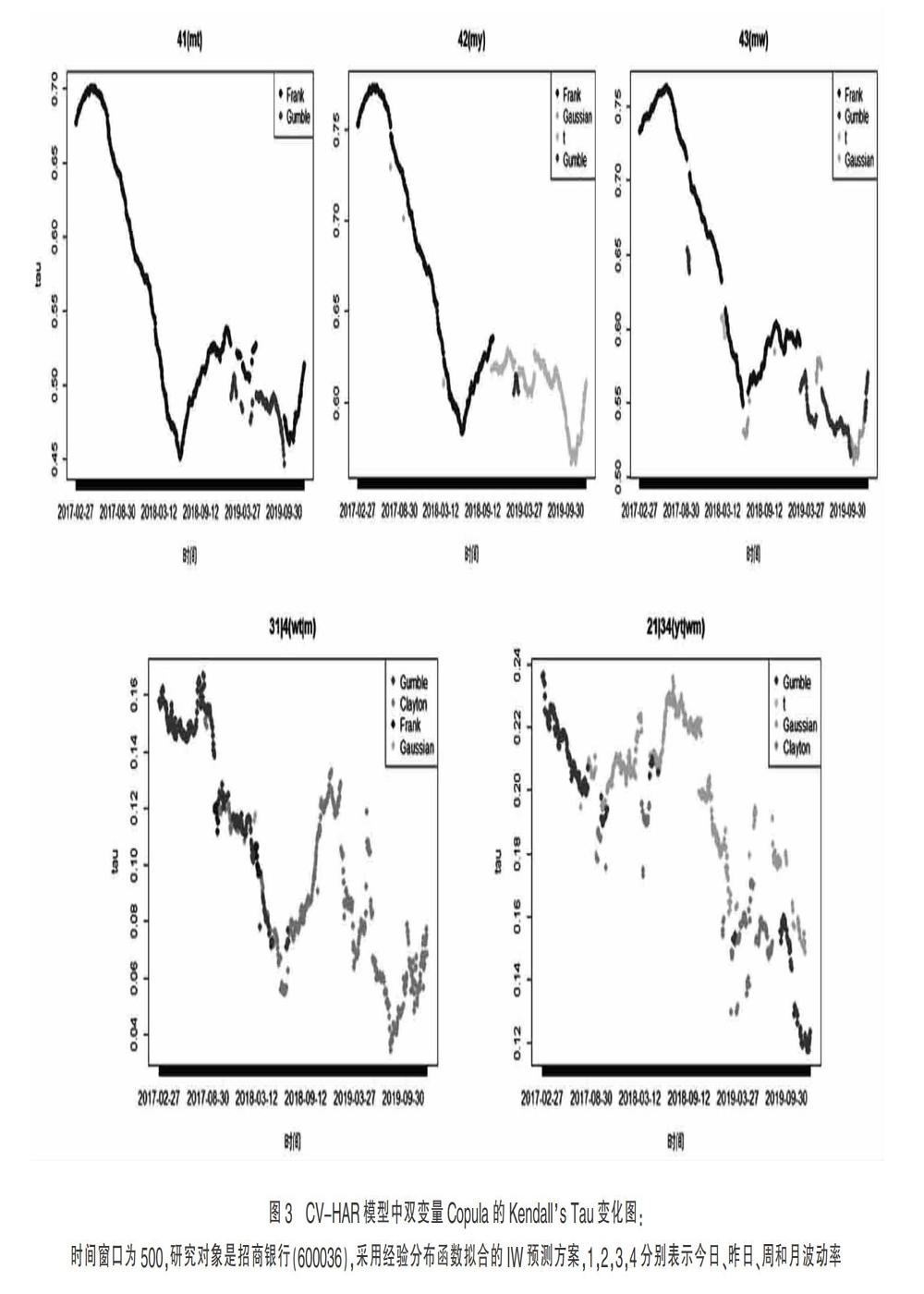
其次，表2展示的是HAR模型和CV-HAR模型在不同窗口下的三种样本外预测方案的性能比较。最为明显是在任意窗口下的不同预测方案呈现的结果都表明CV-HAR模型都要比HAR模型更优秀，这说明本文考虑的模型的确克服了HAR固有的模型限制，并且允许非线性特征的存在，更加灵活地构建了波动率间的依赖关系，从而获得更精准的预测结果。此外，表中基于IW和RW方案的预测结果都显著的比FW方案好，这是因为IW和RW方案考虑了变量间的时变特征，这种变化是FW方法无法描述的。图3给出了CV-HAR模型在IW方案下的Copula依赖关系变化趋势。可以看出，随着时间的变化，双变量Copula的选择各不相同，其Kendall's Tau相关系数也会随着变化，这充分展现了Copula灵活刻画变量间依赖关系的特点。

四、结语

本文使用藤Copula对不同尺度波动率形式的联合分布进行建模，并在此基础上对波动率进行预测分析。在实证分析中，本文收集了上海证券交易所中20支股票的5分钟高频交易数据（计算已实现核波动率，RK）作为研究样本，并采用了不同的建模和预测方案（FW、IW和RW）来比较模型的性能。研究分析表明本文模型相比于HAR模型有着明显的优势，CV-HAR模型不将任何函数结构强加于条件期望（即变量间的线性关系），而是借助藤Copula允许更一般的函数连接不同波动率形式，对波动率的条件期望估计考虑了直接从联合分布中提取，并没有任何函数形式限制，放宽了原始HAR模型线性形式，结果也显示都很大程度上的改进。

参考文献：

[1]Torben G. Andersen and Tim Bollerslev.Answering the Skeptics： Yes， Standard Volatility Models do Provide Accurate Forecasts[J].International Economic Review，1998，39（04）：885-905.

[2]Fulvio Corsi.A Simple Approximate Long-Memory Model of Realized Volatility[J].JOURNAL OF FINANCIAL ECON OMETRICS，2009，7（02）：174-196.

[3]Nelsen，R.B.An introduction to copulas[J].Technometrics，2000，42（03）.

[4]Harry Joe.Families of m-Variate Distributions with Given Margins and m（m-1）/2 Bivariate Dependence Parameters[J].Lecture Notes-Monograph Series，1996，28：120-141.

[5]Barndorff-Nielsen，O.E.，Hansen，P. R.，Lunde，A.，& Shephard，N.Designing realized kernels to measure the ex post variation of equity prices in the presence of noise[J].Econometrica，2008，76（06）：1481-1536.

（作者單位：昆明理工大学理学院）