循环冲击状态下砂岩力学及损伤特性研究

2021-03-24甘德清田晓曦刘志义

中国矿业 2021年3期

甘德清，田晓曦，刘志义，高锋

(1.华北理工大学矿业工程学院，河北唐山 063210；2.河北省矿业开发与安全技术实验室，河北唐山 063210)

近年来，随着我国经济建设快速发展，各类岩体工程项目逐渐增多，同时也出现了许多新的问题亟待解决[1]。在矿山地下开采过程中，由于围岩的失稳破坏造成安全事故往往不是由单次冲击荷载作用产生的，而是围岩承受爆破、机械钻凿等循环动力扰动，在多次冲击荷载下围岩内部微孔隙不断扩展、发育甚至形成贯通裂纹，进而出现失稳现象，该过程可认为是动态循环冲击作用[2]。因此，研究岩石在循环冲击荷载状态下的力学特性、能量耗散规律进而探究其损伤演化机理对于工程实践具有重要的实际意义。

目前，针对循环冲击荷载作用下岩石动态失稳破坏问题，已有专家学者做了诸多探讨。林大能等[3]通过在压力机上对大理石试件进行模拟冲击加载试验，分别得到试件冲击损伤度与冲击次数、动态荷载、围压的相关性，当冲击次数和冲击荷载相同时，围压可显著降低试样的损伤速率；王志亮等[4]基于SHPB试验装置对花岗岩进行等幅循环冲击试验，结果表明当以较大幅值冲击岩体后，随着循环次数的增加，最大应变及平均应变率会随之增加，动态强度随之减小，以低入射幅值进行多次冲击后，试样则未发现有明显损伤；WANG等[5]研究经不同温度对花岗岩热处理再循环冲击后的损伤机理，结果表明，当施加200 ℃后的花岗岩其抵抗冲击荷载能力最强；李夕兵等[6]通过Hopkinson压杆装置分别对五种不同龄期的混泥土进行循环冲击试验，提出在每一种龄期下，第一次冲击都有助于提高试样的动态强度，随着循环次数的增加，损伤度逐渐增加，且早龄期的混凝土试样对入射能更敏感，破坏累计损伤与龄期等外界因素几乎无关；李地元等[7]采用改进的Hopkinson压杆试验系统结合声发射设备对花岗岩进行循环冲击试验，结果表明，试件的损伤度与其吸收能密切相关，并呈正相关关系；LI等[8]则是通过以摆锤为动力源驱动Hopkinson压杆对绿砂岩进行循环冲击，从声学特性、裂隙扩展演变等方面揭示了其损伤演化的内在机理；KRAJCINOVIC等[9]提出应变等效假设，将损伤引入应力-应变关系，使得统计学与损伤力学紧密的结合起来并取得巨大进步；金解放等[10]基于一维动静组合加载条件下的循环冲击构建了岩石损伤演化模型，该模型能较好地预测岩石损伤演化的各个阶段。

本文以红砂岩为研究对象，通过分离式SHPB试验装置进行等幅单轴循环冲击试验，研究砂岩在循环冲击荷载作用下损伤至破坏的动态过程，分析能量对岩样产生损伤和破碎的本质作用，揭示损伤随入射应力和冲击次数变化的规律，为岩体工程安全防护及正确评价围岩稳定性提供理论依据。

1 试验原理及方案

目前，针对岩石冲击动力学的研究，常用的试验设备有落锤、分离式Hopkinson压杆、飞片及轻气炮等，其中分离式Hopkinson压杆不仅可以研究中高应变率下岩石变形特征和强度特性，还可以研究冲击过程中能量传递及耗散规律。因此本试验选用SHPB试验装置(图1)。

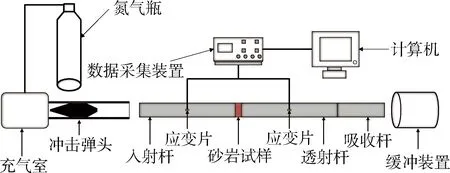
图1 SHPB试验装置示意图

1.1 SHPB试验装置与原理

常规的分离式Hopkinson压杆试验系统由应力发生装置、应力吸收装置、应力传播机构和数据采集系统组成，本次试验装置的所有压杆杆件和冲击弹头材质一致，密度为7 800 kg/m3，入射杆与透射杆长度均为2 m，SHPB杆径为50 mm，弹性模量为210 GPa，纵波波速为5 200 m/s，试验中可以通过纺锤形弹头实现恒应变率的半正弦应力波加载[11]。

通过SHPB试验装置的基本假定，利用接收到的波形，可由式(1)～式(3)得到岩样中应力、应变、应变率以及能耗的关系。

(1)

(2)

(3)

试样的入射能EI、透射能ER、反射能ET计算见式(4)。

(4)

式中：σI(t)、σR(t)、σT(t)分别为某一时刻入射应力、反射应力、透射应力；ρeCe、ρsCs分别为弹性杆和试样的波阻抗；Ls为试样的长度；τ为应力波延续时间；Ae、As分别为弹性杆和试样的截面积。

1.2 砂岩试样的制备及试验方案

本次试验研究采用完整性及均匀性较好的砂岩作为分析试样，加工后的砂岩试样如图2所示。根据已有的研究成果[12]，试样尺寸为Ф50 mm×25 mm。在正式试验前，为了能够达到等辐循环冲击的目的，需进行一定的预试验以确定合适的入射幅值。试验中，需严格控制冲击弹头在发射腔中的位置以及冲击气压的大小，最终确定入射幅值分别为90 MPa、100 MPa、110 MPa、120 MPa，每种幅值选取3个试样。

图2 部分加工完成的砂岩试样

表1为部分试样的初始参数及试验过程中需控制的试验条件，由于数据量较大，限于篇幅，本文仅对具有代表性的试样C-90-2、试样C-100-1、试样C-110-1以及试样C-120-3进行分析。

在进行正式冲击试验之前需在入射杆及透射杆之间均匀涂抹黄油，保证入射杆与透射杆之间、透射杆与吸收杆之间接触良好，然后进行SHPB空冲试验，以检查Hopkinson压杆设备是否有异常，即在不夹持试样的情况下，波形应无反射波，只有入射波与透射波，空冲波形如图3所示。

SHPB冲击试验均以一维假定和均匀性假定为前提[13]，图4为试样C-100-1在第三次冲击过程中的动态应力平衡图。从图4中可以看出，入射端应力曲线(入射应力+反射应力)与透射应力曲线基本重叠，表明冲击载荷作用下砂岩试样处于动态应力平衡状态。

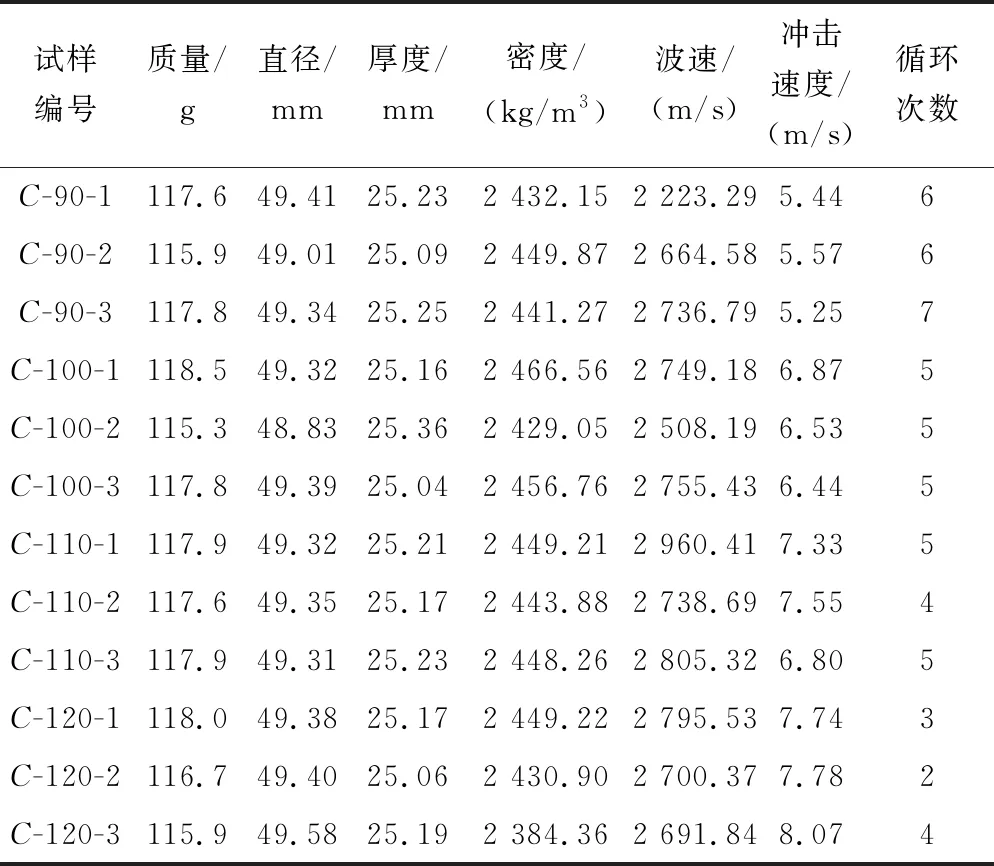
表1 砂岩试样初始参数

图3 空冲波形图

图4 试样C-100-1应力平衡图

2 砂岩循环冲击试验结果及分析

2.1 时程-应变及最大应变分析

图5为循环冲击荷载作用下试样动态应变-时程图。由图5可以看出，当入射幅值为90 MPa时，随着循环次数的增加，试样的动态应变同样是出现先减小后增大的现象，而当入射幅值增加到100 MPa、110 MPa、120 MPa后，动态应变则没有出现减小的现象。主要原因是由于进行低幅值入射能量冲击且循环次数较少时，岩样内部裂隙的压密作用大于损伤作用，此时试样整体的力学性质会优于冲击之前的力学性质；当提高入射能量后，由于冲击速度的增大导致试样内部的裂隙迅速发育、扩展甚至形成贯通裂纹，很大程度上会劣化岩石试样的力学性能，直至出现宏观破坏，岩石试样彻底丧失承载能力。

图5 循环冲击荷载下动态应变-时程图

图6为最大应变与循环冲击次数关系图。由图6可知，随着冲击次数的增加，试样C-100-1、试样C-110-1以及试样C-120-3的最大应变均随之增加，试样C-90-2则是先减小再增加，原因同上，此处不再赘述。

2.2 循环次数与平均应变率分析

砂岩试样在循环冲击过程中的平均应变率随冲击次数的变化规律如图7所示。由图7可知，平均应变率与最大应变随冲击次数的变化规律基本一致，这是由于平均应变率与最大应变都是表征试样变形能力的。随着循环次数的增加，试样C-100-1、试样C-110-1和试样C-120-3的平均应变率随之增加，这是由于砂岩试样累积损伤导致反射系数的绝对值增大，由式(3)可知，当反射波增大时，应变率会随之增大。而试样C-90-2出现先减小后增大的趋势，主要的原因是在低入射幅值和循环次数条件下，压密作用占主导地位，没有造成岩样的损伤反而加固了岩样的稳定性，但随着循环次数进一步增大，试样的破坏程度随之加重。

图6 最大应变与循环冲击次数关系图

图7 平均应变率与循环次数关系图

3 基于Weibull分布的动态统计损伤模型

随着岩体领域损伤力学的发展，岩体统计损伤理论也逐渐得到完善，将统计学理论应用到损伤力学上，利用数学模型统计结果来定量描述损伤度并推导其演化过程，再通过等效性假设等方法，建立损伤模型。目前，较常用的描述损伤分布规律的模型有正态分布、幂函数分布、Harris分布以及Weibull分布等，其中Weibull分布的损伤模型应用更为广泛。该模型提出在动态加载过程中，由于微裂隙和孔隙的积聚导致材料逐渐失去承载能力可以用损伤度D来表征。现假设岩石材料微元强度服从Weibull分布，那么该岩石材料的损伤度D也服从该分布[14]，其概率密度P(F)表达式为式(5)。

(5)

式中：F为微元体的强度分布变量；m和F0为Weibull分布参数，由此可以推出损伤度D的表达式，见式(6)。

(6)

其中，F计算见式(7)。

(7)

式中：α0为岩石材料微元强度参数(可根据Drucker-Prager破坏准则获取[15])；E为弹性模量；ε1为有效应变。

由于之前的许多动态模型都无法准确反映岩石材料的损伤变形特征，本文采用Kelvin模型改进的岩石时效损伤模型[16](图8)，同时通过该模型推导出式(8)。

(8)

式中，η为黏性系数，可由岩石蠕变试验获取，一般岩石的黏性系数取0.1～0.5。

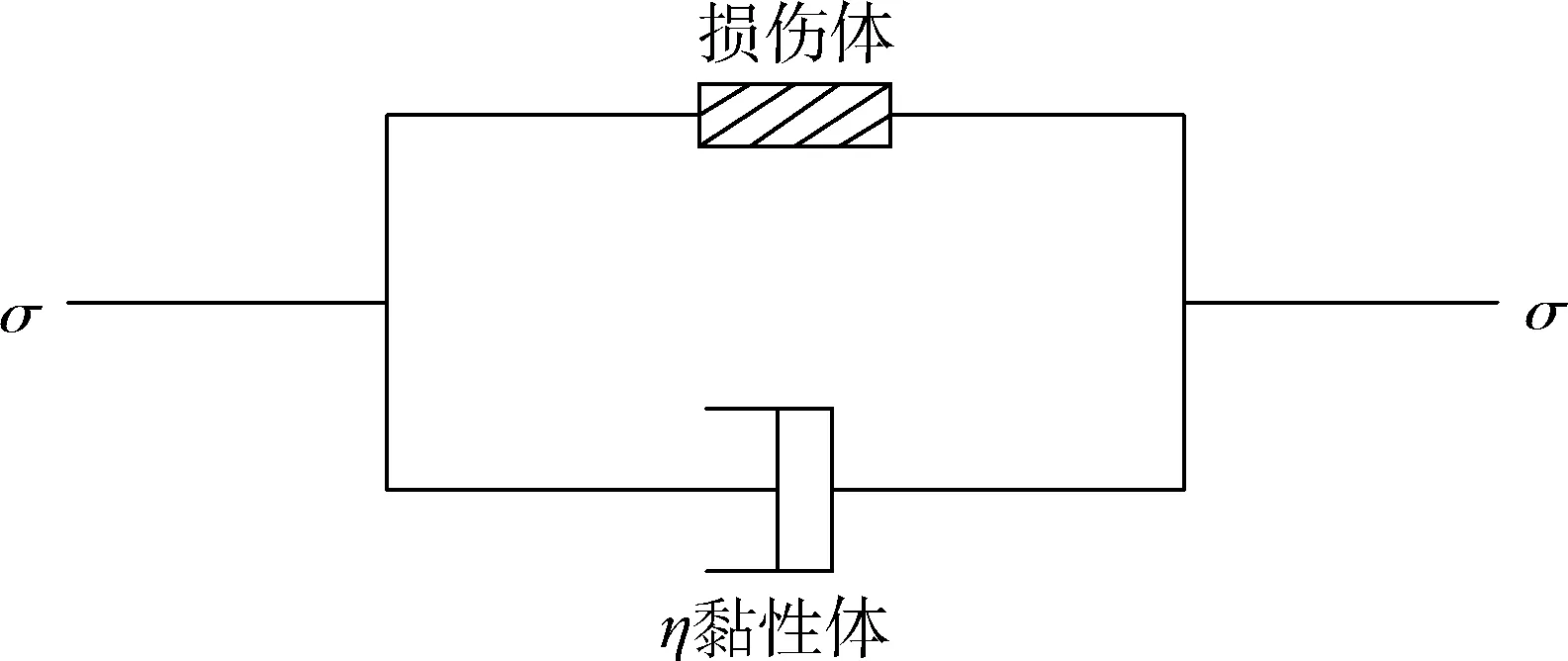
图8 时效损伤模型

将式(6)代入式(8)可得式(9)。

(9)

由应力-应变曲线和时程-应变曲线可以得知，在(σm，εm)点处，存在dε/dt=0，σm为峰值强度，εm为峰值应变。由此可得式(10)。

(10)

再将式(7)代入式(9)可得式(11)。

(11)

再将式(7)和式(10)代入式(6)可得式(12)。

(12)

由式(12)可知，通过冲击试验完成后的试验数据对试样损伤度可以进行计算。为了验证该模型描述动态损伤特征是否正确，有必要对此模型进行验证，因为Weibull分布是根据每次冲击完成后所得到的应力-应变曲线数据来计算岩石的冲击损伤度，所以当进行循环冲击时，除第一次冲击以外，每次冲击损伤度的计算相当于以前一次冲击为基础的。由此根据最终破坏时损伤度为1，本文循环冲击累积损伤采用式(13)计算。

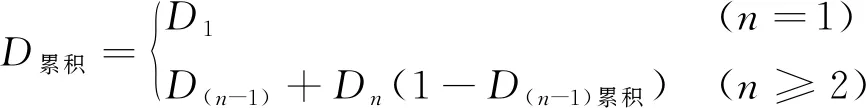
(13)

式中：Dn为第n次循环冲击后产生的损伤；D(n-1)累积为第n-1次累积损伤；n为循环冲击次数。

根据每块试样每次冲击完成后的实验数据，采用Weibull分布计算不同入射幅值砂岩的损伤度，结果见表2。

通过文献[6]可以得到，当试样出现大块破碎时，其损伤度在0.850左右；出现完全破碎后，其损伤度在0.950左右，即试样完全失去承载能力介于二者之间，而本次循环冲击试验中，均未出现完全破碎的情况。从表2中可以看出，试样C-100-1的损伤度为0.857，在第五次冲击结束后，破碎为两块；试样C-90-2、试样C-110-1以及试样C-120-3的损伤度分别为0.796、0.759和0.750，在最后一次冲击完成后，均有程度较轻的破坏，但无法再继续进行循环冲击试验，破碎后的试样如图9所示。综上可知，该模型可用于描述循环冲击荷载作用下砂岩的损伤特性。

图9 试样C-100-1破碎实物图

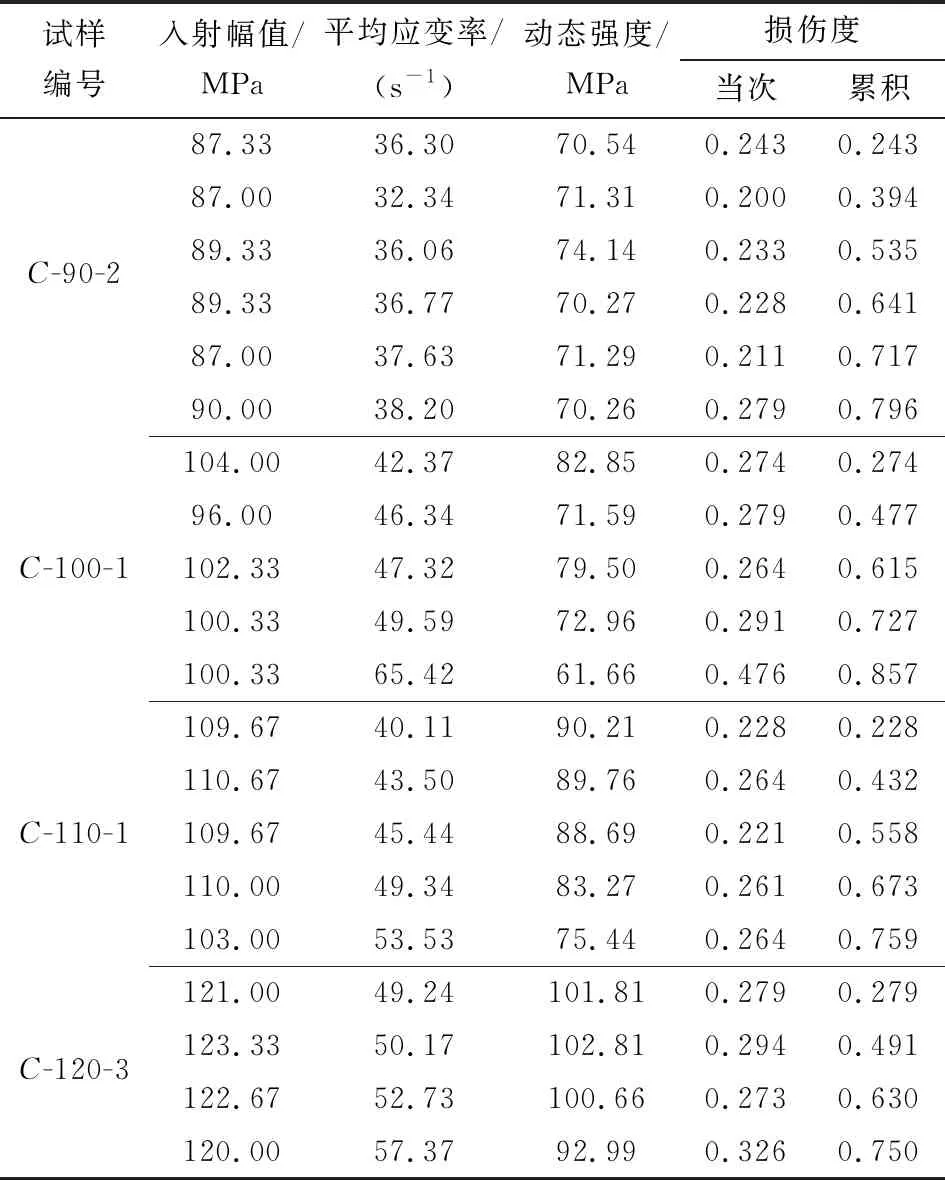
表2 循环冲击条件下砂岩加载条件及损伤度

4 循环冲击作用下砂岩损伤演化特征研究

用较低的能量循环冲击岩石或矿石试件时，在所用能量能够引起试件内部损伤的条件下，每次冲击试件都会产生新的损伤，新产生的损伤是在上一次冲击损伤的基础上发展的，即每次冲击后试件的损伤都是历史损伤的累积。裂隙的活动是岩石损伤的具体形式，新裂隙萌生时需要破坏晶体键并克服分子间的范德华力，所需要的能量大于原生裂隙扩展的耗散能。裂隙的扩展实际上是能量传递过程中在裂隙尖角位置聚集，破坏颗粒间黏聚力引发颗粒运动分离的表现[17-19]。

图10为不同幅值作用下砂岩试样应力-应变损伤曲线图。由图10可知，在达到峰值动态强度之前，曲线大致规律基本一致，曲线开始阶段可以明显看到一段斜率较小的曲线段，该段为压密阶段；由于SHPB冲击发生较快，该阶段的时间相对较短，然后出现一段近似直线，此阶段为弹性变形阶段；随后曲线斜率开始逐渐变小，试样进入非线性变形阶段；当达到峰值动态强度后，出现较明显的“应变回弹”现象。随着入射幅值的增加，初始状态相近的岩样出现破坏时的冲击次数明显减少，除试样C-90-2外破坏前最后一次冲击的最大应变也明显增加。经过循环冲击后，试样最终破坏为两块，峰值应力随入射幅值的增加而增大；随循环次数的增多，峰值应力基本呈递减规律，但是试样C-100-1第二次冲击的应力-应变曲线出现异常，这主要是由于第二次冲击时的入射幅值和其他几次相差较大，存在误差；变形模量随循环次数的增加而减小，而试样C-90-2的变形模量变化不明显，出现此现象是由于每一次循环冲击时，高入射幅值都会对红砂岩试样造成有效的损伤，致其力学性质不断劣化，而低幅值及低循环次数条件下，前几次冲击由于试样没有出现宏观破坏，岩样会在卸载段释放储存在内部的部分弹性能。试样内部微裂隙会首先被压密实，波阻抗也会有不同程度的增大，岩样整体的动态强度有所提高；随着冲击次数的进一步增加，岩样内部微裂隙逐渐发育、扩展，形成贯通裂隙直至试样出现宏观破坏。说明当提高入射应力后，随着循环次数的增加，砂岩试样内部损伤度会快速增加，岩样内部微裂隙迅速扩展、发育，直至丧失承载能力[20]。

图10 砂岩循环冲击应力-应变曲线损伤图

各入射幅值冲击条件下其累积损伤度曲线都表现为下凹型，其增长速率由小变大，即在压密阶段及弹性早期阶段，岩样的累积损伤值变化较平缓，当应力-应变曲线进入非线性变形阶段，损伤开始上升，当达到峰值应力后，损伤度急剧增加，且纵观损伤度曲线，随着循环次数的增加，损伤度也在随之增加，破坏为大块后，损伤度均在0.800左右，这说明最终破坏为大块后的损伤值是反映材料发生破坏时的固有属性，与冲击加载条件基本无关。出现此现象的原因为冲击早期试样首先被压密及弹性变形，但具有可恢复性，此时并不会出现较大的损伤，但随着循环次数的增加，岩样内部裂隙不断扩展、发育甚至贯通为较大裂隙，累积损伤快速增加，直至出现宏观破坏。

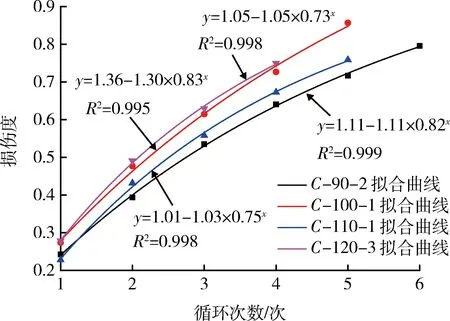
图11 循环次数与损伤度关系图

为了进一步分析循环次数对损伤的影响，本文对不同循环次数下各入射幅值对应的损伤度进行了分析。图11为循环次数与损伤度关系图。从图11中可以得出，循环次数与损伤度为指数函数关系，即曲线呈下凹型，且拟合度都为0.950以上，效果较好；随着循环次数的增加，损伤度不断增加，最终趋于平缓。同一冲击次数相比，入射幅值越大，单次冲击造成的损伤越严重，这说明在实际工程中，应严格控制单次爆破采用的炸药量或隔离措施，尽量降低外界动力扰动对其造成损伤。

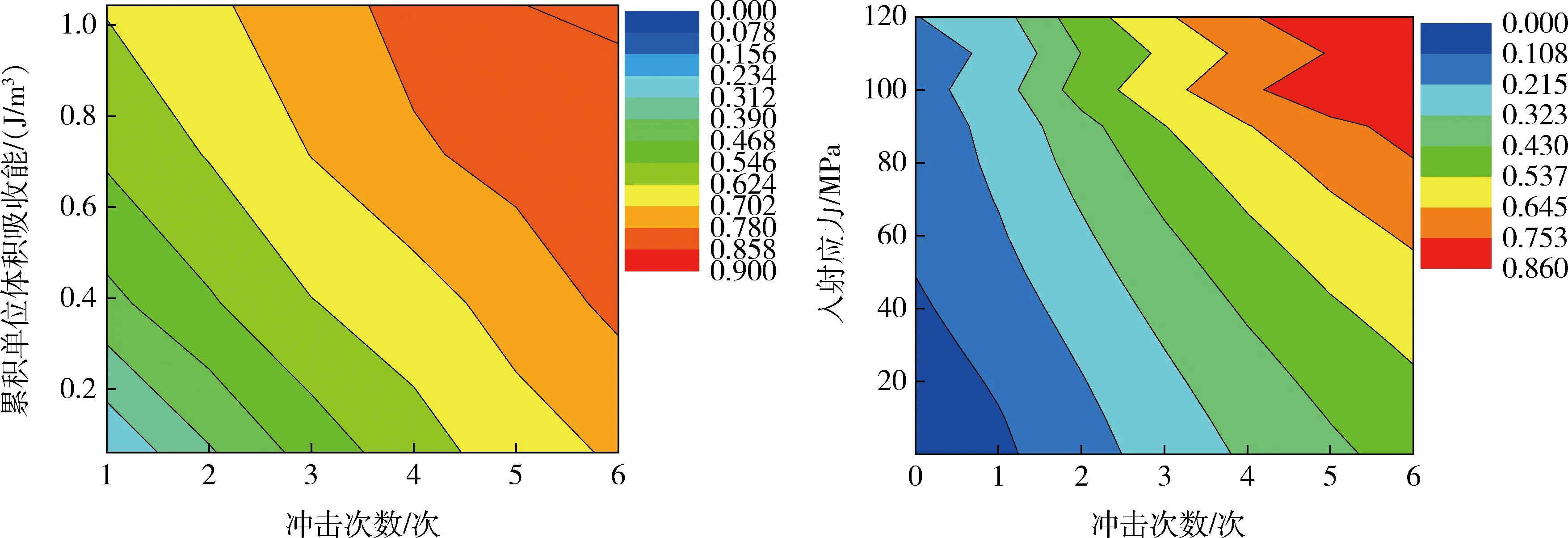
图12 冲击次数、累积单位体积吸收能及入射应力对损伤影响的响应面图

图12为累积单位体积吸收能与累积损伤度关系图。由图12可知，随着循环次数及入射幅值的增大，其累积单位体积吸收能和累积损伤度逐渐增加，到岩样破坏时趋于平缓，说明随着循环冲击的进行，岩样不断吸收能量用于裂纹的扩展及发育，当临近破坏时，试样内部已损伤较严重，再经一次外界相同动力扰动后，岩样发生破坏，大幅降低其承载能力。