基于SNPP-VIIRS夜间灯光数据的GDP预测模型对比

詹淇雯, 胡为安, 刘传立

(1.江西理工大学 土木与测绘工程学院, 江西 赣州 341000; 2.广东工贸职业技术学院, 广州 510510)

0 引 言

夜间灯光数据作为一种新型数据源, 用于记录全球范围内的夜间灯光亮度, 在估算社会经济参量指标方面表现出巨大的潜力和应用前景[1-2]。20世纪70年代, 美国军事气象卫星(defense meteorological satellite program, DMSP)搭载的线性扫描系统(operational linescan system, OLS)设计初衷是为了探测月光照射下的云层分布信息, 而专家学者意外发现DMSP-OLS可记录夜间无云条件下来自地表城镇等发射的可见光辐射, 从此拉开了夜间灯光遥感研究的序幕。夜间灯光影像数据不仅记录了来自城镇的稳定光源, 同时可以捕获森林火灾、 火山喷发和油气燃烧导致的短暂性发光, 因其作为一种长时间序列的数据类型, 具有数据量小、 数据存档丰富和易获取等优点, 被广泛应用于社会经济参量指标估算[3-6]、 城市化[7-9]和城市空间结构演变分析[10-12]、 生态环境和健康效应[13-14]、 重大事件评估[15-17]和渔业[18]等研究领域。随着美国新一代国家极轨卫星(suomi national polar-orbiting partnership, SNPP)搭载的可见光近红外成像辐射(visible infrared imaging radiometer suite, VIIRS)传感器获取的夜间灯光数据存档量不断丰富, 影像数据分辨率更高, 解决了DMSP-OLS数据中发展较快城市中心像元“饱和效应”问题, 长时间序列数据之间可比性和连续性更好, 可为更精细化的社会经济指标预测提供有利的新型数据源。

将夜间灯光影像数据用于GDP的研究较早。Elvidge等[19]基于DMSP-OLS影像数据对美洲数十个国家的GDP与灯光面积进行回归分析, 拟合优度R2达到0.97, 证明可以利用夜间灯光数据估算GDP等社会经济指标。随后, Ebener等[20]利用DMSP-OLS夜间灯光数据对GDP进行估算, 并取得较好的效果; Ghosh等[21]通过夜间灯光数据与美国校正后的经济数据建立回归模型, 成功预测出各州的实际经济状况, 发现该方法可用于核实官方发布的经济数据; 颜定勇[22]利用Copula函数和条件分布函数构建EEMD-SVR-Copula模型用于GDP预测, 预测精度较高; 范强等[23]同样基于DMSP-OLS数据与GDP之间建立多项式预测模型, 证明了该方法可以准确反映研究区的GDP实际增长情况。而目前基于SNPP-VIIRS数据对GDP进行预测的研究较少, 且预测模型仅限单一的函数, 缺乏对比和可行性验证。

鉴于此, 本文利用2012—2019年SNPP-VIIRS月度复合数据, 经过消除负值和不稳定光源等校正处理, 运用线性函数等6种预测模型对江西省GDP进行预测, 以拟合优度和相对误差等指标对各模型预测效果进行对比。为校正SNPP-VIIRS影像数据提供了新思路, 弥补了传统调查方法的缺陷, 同时为相关研究提供学术参考。

1 研究区域与数据来源

1.1 研究区域

江西省位于我国长江中下游南部, 界于113°34′36″E—118°28′58″E、 24°29′14″N—30°04′41″N(图1), 东接福建、 广东, 西邻湖北, 南望广东, 北枕湖北、 安徽, 同时被誉为新中国红色摇篮。北面为鄱阳湖, 其他三面环山, 地形以丘陵和山地为主, 平原为辅, 常年温和多雨, 四季分明。辖11个地级市, 27个市辖区, 12个县级市, 61个县, 共100个县级行政区划。截至2019年, 地区生产总值GDP为24 757.54亿元, 年末常住人口4 666.10万。优越的地理位置、 丰富的雨水资源和矿物资源、 醇厚的优秀红色文化为江西的快速发展奠定了良好的基础。 GDP是评估地区发展状况的重要经济指标, 利用夜间灯光遥感数据预测江西省的GDP, 对比不同预测模型的预测效果显得极具研究意义。

图1 江西省地理位置

1.2 数据来源

(1)江西省和各市行政区划矢量数据。行政区划数据来源于国家基础地理信息中心1∶ 400万数据库。

(2)GDP经济指标数据。该数据来源于中国国家统计局(http://www.stats.gov.cn/)和江西省统计局(http://tjj.jiangxi.gov.cn/)， 其中省级数据包括江西省8年的GDP统计数据, 市级数据包含江西省11个地级市8年的GDP统计数据。

(3)SNPP-VIIRS夜光影像数据。SNPP-VIIRS影像数据来源于美国科罗拉多矿业大学, 可通过网址https://eogdata.mines.edu/download_dnb_composites.html进行获取。与前一代DMSP-OLS数据相比, SNPP-VIIRS在空间分辨率、 时间分辨率和光谱分辨率方面均有较大提升, 各卫星间进行星上定标操作, 且具有更广的辐射范围, 解决了在城市中心存在像元“饱和效应”问题。用于探测夜间灯光辐射的DNB(day night band)波段, 光谱分辨率14 bit, 波长范围0.5～0.9 μm, 所能检测到的灯光辐射亮度下限由5×10-10W/(sr·cm2)提升至2×10-11W/(sr·cm2), 这就意味着在影像数据中可记录夜晚更微弱的灯光信息, 可为研究精细化的人类社会活动提供可靠的新数据源。该数据分为年度复合和月度复合数据， 年度数据存档较少, 用于时间序列的年际变化研究略显不足, 而月度数据较为丰富, 共发布95期。由于夏季影像易受植被影响, 冬季影像受冰雪影响, 因此本文选择2012—2019年10月份复合数据进行研究, “*.vcm”格式的影像数据与“*.vcmsl”相比, 完全排除杂散光的影响, 数据质量更佳。

2 研究方法

SNPP-VIIRS不但继承了OLS传感器的微光探测能力, 增强了探测敏感度, 提高了时空分辨率和光谱分辨率, 而且不存在像元DN值“饱和”问题, 影像数据在时间尺度可对比性和连续性更强, 在监测人类社会活动和自然现象等方面更具应用潜力, 但也正因为VIIRS传感器对辐射光源的高度灵敏性, 导致数据中也存在背景噪声等问题, 需进行校正处理。以江西省为研究区, SNPP-VIIRS月度复合影像为研究数据, 利用2012—2018年的GDP统计数据与灯光强度数据, 基于线性函数等常用的预测模型外, 引入Gaussian函数预测2019年江西省的GDP值。具体思路为: ① 数据预处理: 首先将我国区域的SNPP-VIIRS夜间灯光影像数据投影至符合我国地形的Albers投影坐标系, 设置其参数Central_Meridian为105°, Standard_Parallel_1为25°, Standard_Parallel_2为47°, 采用最邻近法将影像栅格大小调整为500 m×500 m, 同时利用研究区域的行政边界数据对影像数据进行掩膜裁剪, 得到各年份研究区域的NPP-VIIRS夜间灯光影像; ② 影像校正: 针对月度复合影像数据中存在负值和背景噪声等问题, 利用标准年度数据对其进行校正操作; ③ 数据质量验证: 选取南昌市为样本区域, 以GDP和年末常住人口为经济指标, 拟合优度R2和显著性P值作为评价标准, 验证数据质量; ④ GDP预测: 利用多种函数预测模型对2019年江西省GDP进行预测, 对比拟合优度和相对误差等指标分析各模型的预测效果。

2.1 负值消除

通过对像元DN值进行提取， 发现影像数据中存在负值现象， 该现象主要发生在夏季高纬度地区以及西南地区， 负值数值较小, 但数量较多, 该问题的存在必定会影响数据质量和研究结果的准确性， 因此需要对负值进行消除。目前, 解决负值问题的常用方法有两种: 一是利用DMSP-OLS夜间灯光数据中不存在负值问题的特性消除负值, 该方法科学有效, 但因两种影像数据分辨率不同, 导致校正过程复杂, 且不适合长时间序列的数据校正; 二是将负值像元赋予0值, 该方法简单易操作, 针对时间序列数据校正效果好。鉴于此, 本文采用第二种方法消除负值:

(1)

其中,DNx表示校正前的像元DN值;DNy表示校正后的像元DN值。

2.2 短暂光源与背景噪声消除

VIIRS传感器接收到的能量信息中不仅包含稳定的城镇夜间灯光, 同时也将探测到地表发射的月光、 闪电和诸多噪声因子(高能粒子与大气层碰撞火光)等短暂性光源。数据说明文件显示, 月度复合数据未进行去光处理, 短暂光源与背景噪声仍被保留, 因此需要对影像进一步校正。科罗拉多矿业大学发布了2015—2016年已经去除短暂光源和背景噪声的两期年度标准数据, 考虑到两期数据年份相近, 仅选择2015年的标准年度数据校正2015年月度复合数据。将标准年度数据按照DN≤0赋值为0、DN>0赋值为1(表示稳定光源区域), 生成掩膜数据; 将2015年月度数据乘以掩膜数据去除短暂性光源和背景值, 获得2015年校正的月度数据。

由于短暂光源存在时间较短, 不可能同时存在于相邻年份数据的同一地理位置, 可认为在上一年(下一年)的灯光未在下一年(上一年)数据中出现, 即为短暂性光源。相邻年份的稳定光源及像元DN值应变化不大, 因此， 以经过校正的2015年月度数据中稳定区域为基准, 对其他年份数据进行校正。分别提取其他各年影像的掩膜数据, 2012—2014年影像按照式(2)提取稳定灯光区域, 2016—2019年按照式(3)提取稳定灯光区域, 最后将稳定灯光区域与对应年份的数据相乘, 得到去除短暂光源与背景噪声的校正影像。

(2)

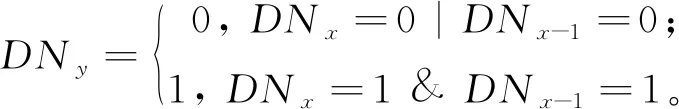
(3)

式中:DNx表示校正年份的DN值;DNx+1表示校正年份下一年的DN值;DNx-1表示校正年份上一年的DN值;DNy表示校正年份的稳定光源DN值。

2.3 极高值消除与连续校正

由于地表河流湖泊等高反射表面和大功率渔船照明等因素的影响, 极易对局部影像数据造成局部扰动, 表现为像元DN值异常, 数值较大, 远远超出实际情况, 需要对影像进一步校正处理。针对异常极高值问题, 本文参考胡为安等[24]提出的解决方法, 首先基于ArcGIS平台分别对各年影像数据像元DN进行提取, 按照顺序或逆序进行排列, 基于统计学原理获得2012—2019年江西省最大灯光亮度值分别为61.41、 72.65、 83.86、 93.96、 104.39、 118.47、 135.86和151.34。若像元DN值大于该年最大灯光亮度值, 即可认为其为极高值, 利用最大灯光亮度值将异常极高值像元进行替换, 消除极高值对数据质量的影响。

我国作为世界上最大的发展中国家, 2012—2019年间的城市化进程和经济状况等均处于快速发展阶段, 未出现衰退现象。因此, 下一年的灯光亮度值不低于上一年同一地理位置的灯光亮度值, 依据此理论, 以2012年影像数据为基准, 2013—2019年数据按照式(4)依次进行校正, 增强时间序列数据的可比性与连续性。

(4)

2.4 多种GDP预测模型建立

研究表明, 单个像元覆盖地表大约2.5×105m2区域, 其灯光辐射亮度值易受周围环境的影响, 无法利用其与GDP构建预测模型， 而区域灯光总强度与人类社会活动指标间存在高度相关性早已被证实, 因此, 构建区域灯光总强度指标(total night light index, TNLI)计算式进行GDP预测:

(5)

式中：DNm表示第m级的亮度值;nm表示像元数量。

鉴于之前相关研究多采用线性函数等单一的函数模型进行GDP预测, 仅以相关性拟合优度作为评价标准, 未对校正数据进行质量验证, 缺乏从多视角、 多维度研究GDP预测问题。因此, 如表1所示, 本文选取常用的5种函数预测模型外, 引入Gaussian函数, 从多方面比较各函数预测效果。

表1 6种函数预测模型

目前基于夜间灯光影像数据进行社会经济参量指标预测的研究, 对精度评价的方法主要有两种:

一是通过相对误差的方式检验预测值与统计值间的接近程度

(6)

另一种则是利用预测值与统计值进行回归分析, 利用拟合优度等指标对预测精度进行评定, 该方法适用于预测数据与统计数据间存在明显的线性关系。为对比各函数模型的预测效果, 本文同时采用上述两种方法对预测GDP精度进行验证。

3 结果与分析

3.1 数据质量验证

为验证影像数据校正方法的合理性和科学性, 分别进行定性和定量分析对比。定性采用目视解译法, 从直观的视觉角度分析影像校正前后的变化。校正前的影像中存在负值现象, 几乎所有区域均被大量的背景噪声覆盖, 时间序列的影像数据缺乏可比性和连续性(图2); 校正后的影像, 去除了负值像元、 背景噪声和短暂光源, 最小DN值为0, 最大DN值逐年递增, 城市空间结构清晰可见, 城市化扩张得到有利凸显, 符合实际情况(图3)。

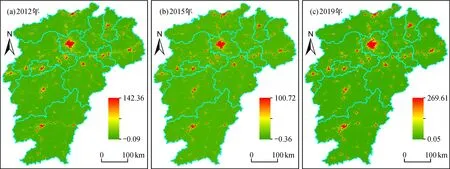
图2 2012、2015和2019年DN值校正前影像

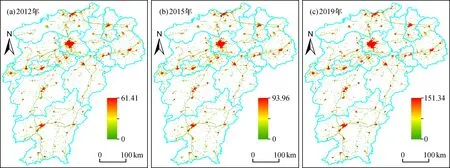
图3 2012、2015和2019年DN值校正后影像

定量分析则选取省会南昌作为样本区, 提取校正前后影像中的TNLI与社会经济参量指标进行拟合能力对比。校正前TNLI与GDP、 年末常住人口的拟合优度R2分别为0.720 5、 0.652 9, 经过校正后的拟合优度R2分别提升至0.961 8和0.960 2(图4、 图5)。为了检验拟合方程的可信度, 采用皮尔逊相关性来检验线性关系与拟合方程系数是否具有统计学意义。结果表明, TNLI与GDP、 年末常住人口的皮尔逊相关性为0.98和0.97, 且通过了0.01级别(双尾)显著性检验, 进一步说明校正方法的可靠性和科学性, 校正后的数据可用于年际变化的GDP预测研究。

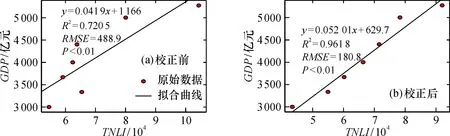
图4 校正前后TNLI与社会经济指标拟合效果对比

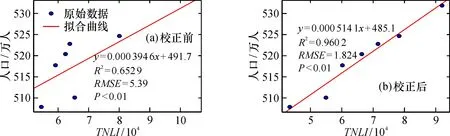
图5 校正前后TNLI与人口指标拟合效果对比

3.2 计算结果与分析

基于ArcGIS平台对2012—2018年江西省TNLI进行提取, 采用线性函数等6种模型分别对TNLI与统计局整理的GDP数据进行回归分析, 回归结果如图6所示。各函数模型的拟合优R2均在0.9以上, 且通过了0.01级别(双尾)显著性检验, 说明文中所选指标与GDP间存在极高的相关性, 而且利用该指标可以对GDP进行预测分析。其中, 二项式函数的回归效果最佳, 拟合优度R2达0.967 0。

图6 6类预测模型与TNLI的回归结果

按照图4、 5中的回归预测模型方程, 将所提取的江西省2019年TNLI代入各函数模型方程, 预测结果如表2所示。6种函数预测模型相对误差绝对值均小于10%, 小于2%的有3种, 分别是二项式函数、 指数函数和Gaussian函数; 其中新引入的Gaussian函数模型预测效果最佳, 绝对误差为-285.29亿元, 相对误差仅为-1.15%, 对数函数模型预测结果误差较大, 相对误差为8.65%。

表2 各模型预测值与误差

在上述省级尺度下, 利用2012—2018年已有统计GDP数据结合TNLI预测2019年的省级GDP总值。为在更精细尺度上研究各函数模型的预测效果, 有必要在市级尺度上分析各模型的预测效果, 将2012—2018年江西省11个地级市的GDP统计数据与TNLI进行回归分析, 求解预测模型方程, 并将2019年各年TNLI代入模型求解各城市的GDP预测值, 预测结果见表3。在市级尺度下, Gaussian函数预测模型由于函数特性限制, 导致无法对九江和鹰潭两个城市进行预测外, 其他函数预测相对误差绝对值均小于10%, 对数函数模型预测结果相对误差较大, 二项式函数预测效果最佳, 相对误差仅为-0.68%。

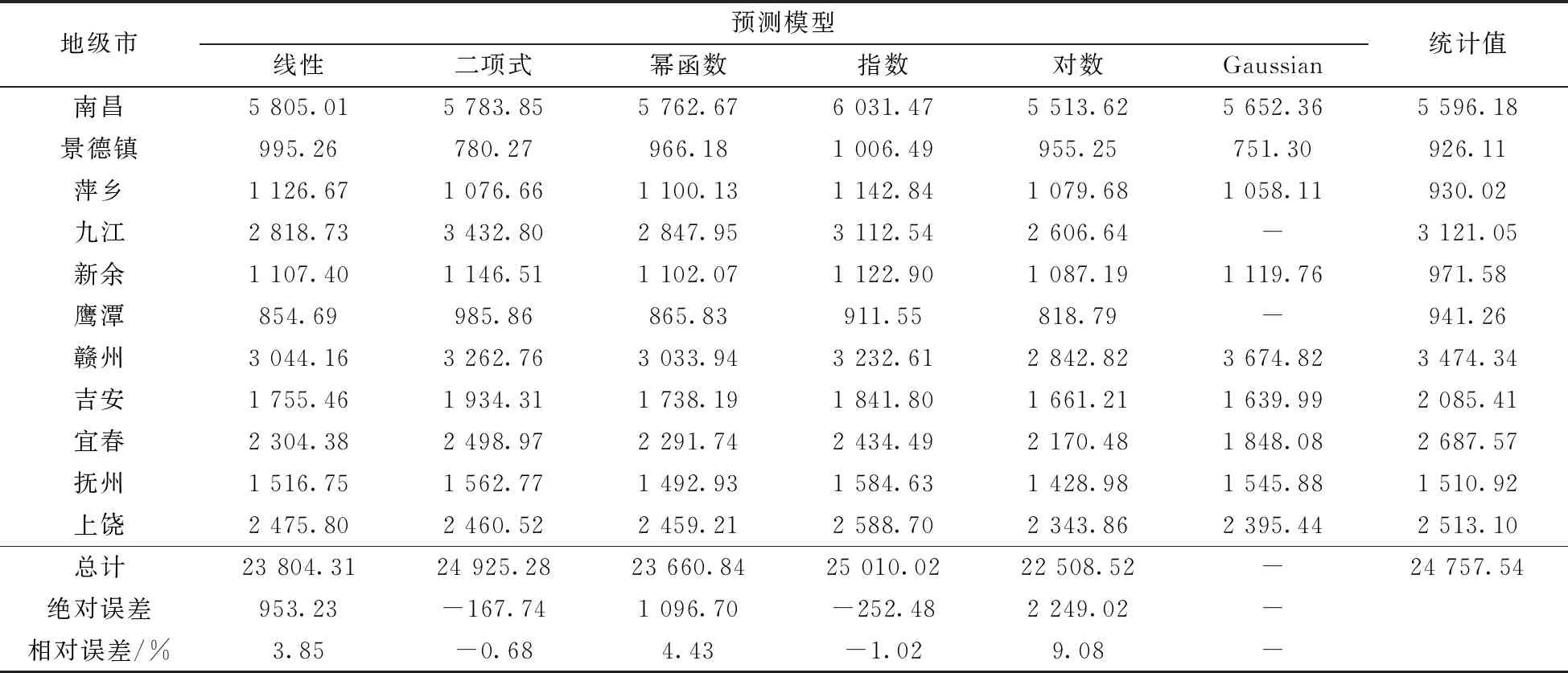
表3 2019年江西省地级市GDP预测结果

通过将各模型预测值与统计值进行回归分析, 基于相关性拟合优度R2和均方根误差RMSE进行预测效果评定, 通过了0.01级别显著性检验, 分析结果如图7所示。各函数模型均表现出较好的预测效果, 拟合优度均大于0.95, 其中二次函数预测模型预测效果最佳, 拟合优度为0.985 8,RMSE为182.4, 均优于其他函数模型。

图7 2019年城市GDP预测值与统计值回归结果

4 结束语

GDP数据对于科学研究和国家决策具有重要的参考价值, 鉴于获取该数据多采用抽样调查统计等传统方式, 在此过程中需要消耗大量的财力、 物力和人力资源, 同时存在人为因素的干扰、 缺乏地理空间信息以及数据更新存在滞后性等缺点。夜间灯光影像数据与人类活动密切相关, 具有独立客观、 空间信息和时空连续等特性, 因此夜间灯光数据可用于社会经济参量估算研究。

由于目前研究多采用DMSP-OLS数据进行GDP预测, 且多采用单一的函数模型, 缺乏对比和可行性验证。随着第二代夜间灯光数据SNPP-VIIRS的陆续发布, 数据存档量逐渐丰富, 使长时间序列的年际变化研究成为可能。 研究证明， 与DMSP-OLS数据相比, SNPP-VIIRS数据更具发展潜力。因此, 本文选取10月份的SNPP-VIIRS月度复合数据, 经过消除负值和稳定光源等校正操作, 对比了线性函数等6种函数模型的预测效果, 发现在省级尺度下, 二项式函数拟合优度最高, Gaussian函数预测效果最好； 市级尺度下, 二项式函数均优于其他函数模型。本文研究结果为SNPP-VIIRS校正提供了新思路, 也为相关科学研究和政府决策提供了学术参考。