基于WOA-LSSVM算法的区域GNSS高程异常拟合方法

何广焕, 唐诗华, 邢鹏威, 张 跃, 蒙金龙

(桂林理工大学 a.测绘地理信息学院; b.广西空间信息与测绘重点实验室, 广西 桂林 541006)

0 引 言

全球导航卫星系统(GNSS)是与现代科学技术发展同步兴起的先进导航、 定位技术[1]。现今GNSS技术已经成为快速收集地理数据的重要手段, 但其获取的高程是以参考椭球面为基准的大地高, 而在实际测量工程项目中, 采集的高程数据是以似大地水准面为基准的正常高, 这两种高程之间存在的差值, 即高程异常值[2]。为了使GNSS技术能代替传统的水准测量技术, 构建高精度的转换模型一直是测绘工作研究的重点。随着人们对拟合模型构建方法的深入研究, 近年来越来越多的智能算法应用于区域GNSS高程拟合模型的建立[3-4]。孙佳龙等[5]提出通过地形熵聚类优化多面函数高程拟合模型, 将地形熵作为高程数据分类的方法, 再利用多面函数进行高程异常拟合, 取得了很好的拟合效果。蒲伦等[6]提出利用蚁群-遗传算法优化多面函数构建高程拟合模型, 为常规多面函数选取合理的中心节点及光滑因子, 使其拟合模型达到更高的精度。高红等[7]经过对比分析验证了粒子群算法优化最小二乘支持向量机(least squares support vector machine, LSSVM)用于区域高程拟合模型构建的可行性。本文通过鲸鱼算法(whale optimization algorithm, WOA)为LSSVM高程拟合模型寻找正则化参数c和核函数参数σ2, WOA算法具有全局搜索能力强、 参数少、 收敛速度快的特点, 能够较好地解决原拟合模型中难以寻找最佳参数的问题, 进一步提高了区域GNSS高程拟合模型的预测精度。

1 鲸鱼算法

Mirjalili等[8]在受到座头鲸捕食行为的启发后,于2016年提出了鲸鱼算法。WOA还原了鲸鱼的狩猎过程, 通过仿照鲸鱼的捕猎方式去寻找猎物位置最优解, 此过程主要包括了3种行为: 包围猎物、 螺旋气泡捕食、 随机搜索[9]。鲸鱼算法参数少、 收敛速度快、 全局搜索能力强, 适用于多个领域[10]。假设鲸鱼的种群规模为N, 所要求解问题的维度是d, 则第i只鲸鱼在d维空间中的位置可表示为Xi=(x1i,x2i, …,xdi), 其中i=1, 2, 3,…,N。

1.1 包围猎物

鲸鱼在正式捕食前, 需要预估猎物的位置, 而鲸鱼所在的位置可看作待优化问题的解。当领头鲸鱼确定猎物的位置后, 通过信息传递, 其他鲸鱼群也会向目标位置游动, 进而不断更新自己的位置

D=|C·X*(t)-X(t)|;

(1)

X(t+1)=X*(t)-A·D。

(2)

式中:t表示当前种群代数;X*(t)表示t代鲸鱼所确定猎物的最优位置向量;X(t)代表其他鲸鱼种群的个体位置向量; “·”表示逐元素乘法运算;D表示领头鲸鱼与猎物之间的距离向量;X(t+1)为其他鲸鱼向领头鲸鱼靠进而不断更新的位置向量参数;C是控制参数;A是收敛因子。上式可以进一步表示为

(3)

式中:r为[0, 1]中的随机数; 随迭代次数的增加，a由2线性递减到0;ti为当前迭代次数;Tmaxlter是最大迭代次数。

1.2 螺旋气泡捕食

鲸鱼捕食的另一种方法是先估算自身到待捕猎物之间的距离, 然后慢慢靠近猎物的位置, 当到达猎物位置后, 向其吐出螺旋状气泡从而实现捕食

D′=|X*(t)-X(t)|；

(4)

X(t+1)=D′·ebl·cos(2πl)+X*(t)。

(5)

式中:D′表示猎物到第i只鲸鱼的距离向量参数;b代表螺旋状常数, 一般定义为1;l为[-1, 1]的随机数。

由于鲸鱼在捕食的过程中, 包围猎物和螺旋气泡捕食两种行为可同时进行, 因此它们所能发生的概率相同(均为0.5), 可得模型

(6)

式中:p是[0, 1]的随机数。

1.3 随机搜索猎物

鲸鱼在搜索猎物的过程中, 除上述方式外, 还可以进行大范围的随机搜索, 根据猎物位置而随时改变自身位置, 扩大自身的搜索范围, 避免陷入局部最优的境况。此过程可表示为

D=|C·Xrand-X|;

(7)

X(t+1)=Xrand-A·D。

(8)

式中:Xrand是当前代数中其中一条鲸鱼发现猎物的位置。

通过收敛因子A的绝对值来选择更新位置的方式： 当|A|<1时, 进入包围吐泡模式寻找局部最优位置参数; 当|A|≥1时, 鲸鱼进入全局搜索, 避免陷入局部最优。鲸鱼算法具体流程如图1所示。

图1 鲸鱼算法流程

2 WOA-LSSVM拟合模型

2.1 最小二乘支持向量机

最小二乘支持向量机是在原有支持向量机的基础上, 利用最小二乘法将原有支持向量机优化问题的非等式约束用等式约束替换, 使得支持向量机的泛化能力、 全局优化能力增强, 还提高了收敛速度和化简了计算过程[11]。其原理及数学模型为: 给定训练样本集{(x1,y1), (x2,y2),…, (xn,yn)}, 则xn∈Rn表示n维的输入样本,yn∈R为一维输出样本, 通过映射函数φ(x)把输入样本空间的非线性拟合问题映射到高维特征空间的线性拟合问题, 并采用结构风险最小化原则来建立优化问题

(9)

约束条件为

s.t.yi=wT·φ(xi)+b。

(10)

式中:w为权重向量;c为正则化参数, 主要目的在于控制并减少过度拟合;ξ为惩罚变量, 其作用在于引入离群点;b为误差；i=1, 2, …,n。利用Lagrange 乘子ai和KKT (Karush-Kuhn-Tucker)条件优化LSSVM， 可得函数模型

y(x)=ai[φ(xk)φ(xi)]+b。

(11)

先前的过程中, 为了利于对输入样本数据的分类, 将LSSVM函数模型转化为高维特征函数, 增大了计算量。为解决这一问题, 需引入核函数K(x,xi), 优化后得到最终模型

(12)

常用的核函数有径向基核函数、 线性核函数和多项式核函数, 本文采用径向基核函数作为LSSVM的核函数

(13)

式中:σ2为核函数参数。

2.2 WOA-LSSVM建立拟合模型步骤

在实际测量工程中, 直接利用LSSVM来构建区域拟合模型, 最终模型的预测精度往往难以达到要求， 其主要原因在于核函数参数和正则化参数的取值会直接影响模型的预测结果, 不合理的参数设置将会降低模型预测结果的可靠性[12]。本文提出利用鲸鱼算法来寻找LSSVM中的正则化参数c和核函数参数σ2, 代替常规LSSVM中的交叉验证法, 提高参数寻优的全局性, 进而构建较高精度的区域拟合模型。具体过程为: ①读取训练样本数据, 并对其进行归一化处理; ②设定鲸鱼种群参数, 主要有种群大小N、 起始位置(x,y)、 最大迭代次数Tmaxlter、 螺旋气泡形状参数b以及鲸鱼种群位置的上下界; ③将高程拟合模型的残差均方根误差RSME作为每个鲸鱼位置的适应度函数, 以适应度最优个体位置作为猎物位置X*; ④当迭代次数t≤Tmaxlter时, 会不断更新参数a、A、c、l、p; ⑤|A|<1时, 用式(6)更新鲸鱼最优位置; 当|A|≥1时, 用式(8)全局搜索更新鲸鱼最优位置; ⑥每次迭代过程中根据适应度函数确定当前鲸鱼位置, 并与之前鲸鱼的位置进行对比分析, 选出一个最优位置并记录保存, 如果达到最大迭代次数, 则跳出步骤⑥, 否则返回步骤③ 继续执行; ⑦ 输出鲸鱼的最优位置X*, 循环结束后, 将鲸鱼的最优位置作为LSSVM的核参数和正则化参数, 建立区域GNSS高程拟合模型并输出检测结果。

3 算例分析

为验证WOA-LSSVM算法在区域GNSS高程拟合中的稳定性及有效性, 本文分别选取两个不同地形特征的研究区进行测试分析, 检验该组合算法在构建区域GNSS高程拟合模型中的有效可行性。

3.1 带状区域

3.1.1 研究区概况 以杭州跨海大桥为例, 数据来源于文献[13]中杭州跨海大桥实验中的部分GNSS水准重合点, 跨海大桥全长约36 km, 宽度为33 m, 点位分布较广, 主要分成南北两个区域, 中间海中加密网点走向大致呈线形分布。均匀选取28个GNSS水准重合点, 用于组合算法构建拟合模型, 将剩余的12个重合点作为检核点, 具体情况见图2。将鲸鱼的种群数量设置为30头、 最大迭代次数为90、 螺旋状常数设置为1, 为LSSVM选择最合适的参数用于区域拟合模型的构建。

图2 跨海大桥GNSS水准点位分布

3.1.2 拟合模型精度分析 为了验证WOA-LSSVM组合法在GNSS高程拟合中的稳定性及有效性, 将其与常规LSSVM拟合法、 BP神经网络拟合法进行对比分析， 分别统计了10次3种拟合方法建模的内外符合精度, 结果见表1。

表1 不同模型拟合精度统计

可知, 在10次实验之后, 无论是内符合精度还是外符合精度结果, WOA-LSSVM拟合法建模的稳定性均要优于BP神经网络和常规LSSVM拟合法, 且组合算法外符合精度均值为±12.2 mm, 常规LSSVM外符合精度均值为±17.5 mm, 相较于常规LSSVM, 拟合模型预测精度提高了30.3%, 进一步证明了WOA-LSSVM拟合法构建拟合模型的精确性。为了更加清晰直观地展现检核点预测结果的变化趋势, 绘制了12个GNSS水准检核点的高程异常柱状图3。

图3 不同建模方法的高程异常预测值与真实值对比

可见, 不同拟合法构建拟合模型的预测值与真实值之间的近似差值, 其中第12个检核点的预测结果与真实值的差值较大, 相较于其他几个检核点预测结果, 3种方法的预测结果与真实值相比均不太理想, 但WOA-LSSVM法构建的拟合模型预测结果更加接近于真实值, 也表明了改进拟合模型预测结果的精准性有所提高。纵观整个柱状图的变化趋势, 相较于常规LSSVM、 BP神经网络拟合法, 组合算法的拟合结果也更为可靠。

3.2 面状区域

3.2.1 研究区概况 以上实验通过少量带状区域分布的GNSS水准数据来验证了WOA-LSSVM构建区域拟合模型的有效性, 为进一步验证组合算法在实际测量工程中的建模真实性, 在广西东北部某市采集少量GNSS水准数据, 其覆盖面积约为300 km2, 点位分布较为均匀, 考虑到测区地势较为平缓, GNSS水准点间隔在2～2.5 km, 满足三、 四等水准测量的要求。其中选取40个分布均匀的GNSS水准重合点作为拟合点, 剩余的20个点作为检查点(图4)。

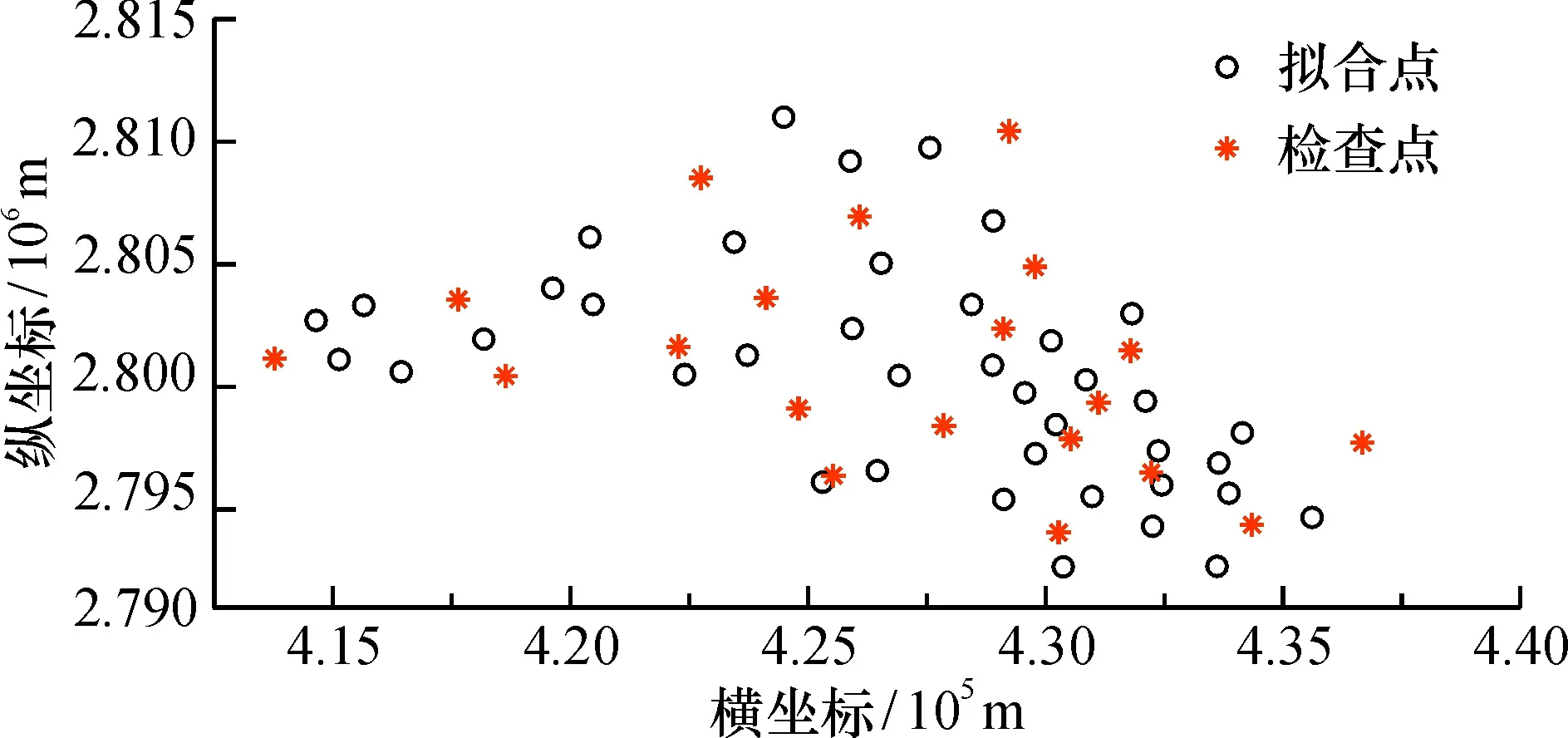
图4 研究区域点位分布

3.2.2 建模结果及分析 将WOA-LSSVM算法的种群数量、 最大迭代次数、 螺旋状常数等参数设置为与3.1节相同， 分别利用3种拟合方法构建区域高程拟合模型后, 检核点通过拟合模型预测其高程异常, 统计了与真实值间的残差值, 并绘制了检核点拟合残差的变化折线图5。

图5 3种拟合方法检核点残差对比

通过拟合残差的波动趋势可以看出, WOA-LSSVM拟合模型预测检核点的残差波动范围要小于BP神经网络拟合法、 常规LSSVM拟合法, 效果最为理想。其中BP神经网络拟合法的波动性最为明显, 也表明BP神经网络拟合法需要得到改进。为了更为直观地了解不同拟合法预测的检核点高程异常值, 对20个检核点的高程异常预测值和残差值进行分析, 结果见表2。

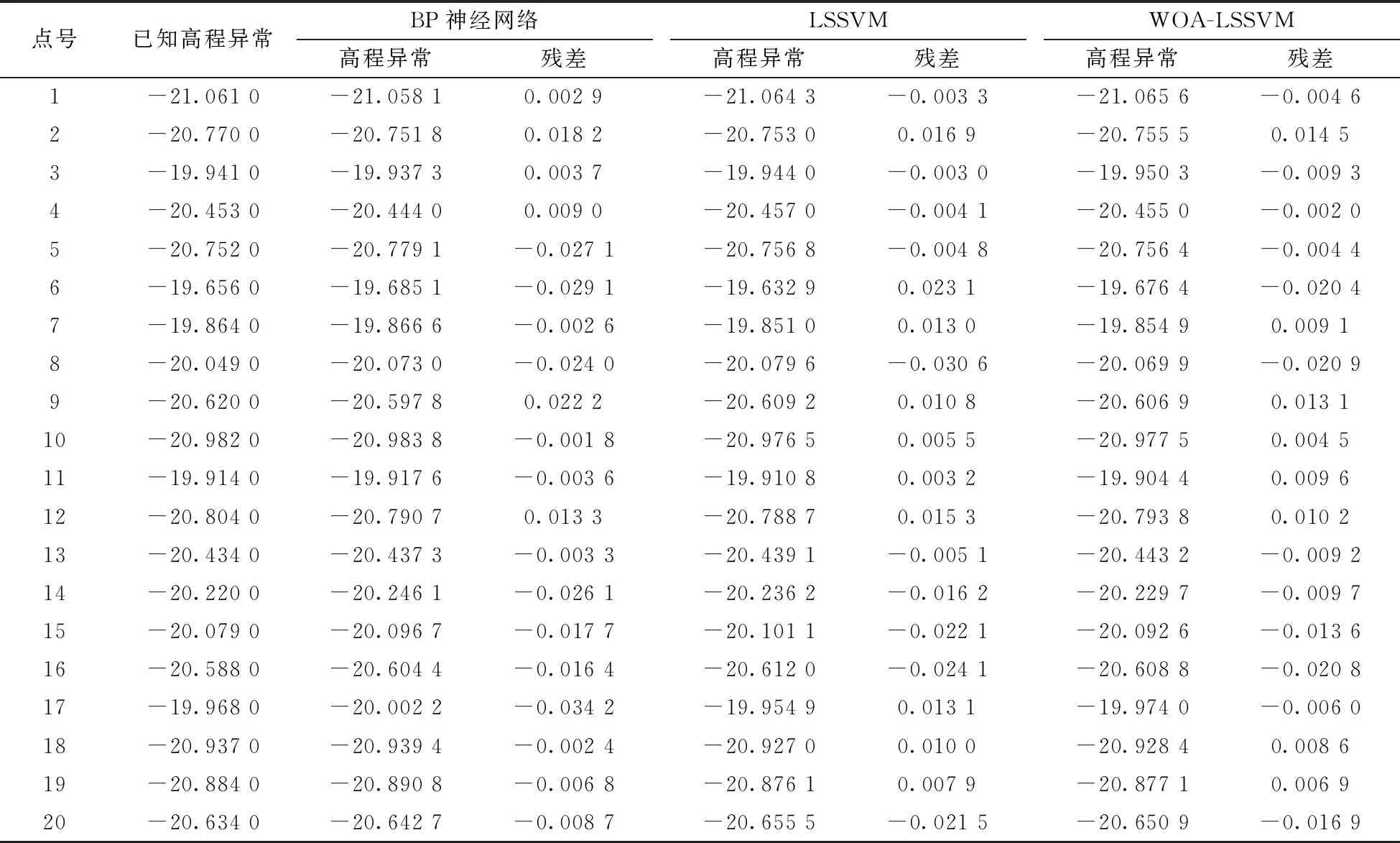
表2 不同拟合模型检核点的预测结果

可知, WOA-LSSVM拟合法建模的拟合残差变化区间为-20.9～14.5 mm, 常规LSSVM拟合模型的残差变化区间为-30.6～23.1 mm, BP神经网络拟合法为-34.2～22.2 mm。相较于其他两种方法, 鲸鱼优化拟合法的残差变化区间最小, 结果最为稳定, 证明了WOA-LSSVM构建区域GNSS高程拟合模型的有效性。为了验明组合算法建模的精准性, 计算了不同方法建模的内外符合精度, 如表3所示。

表3 不同模型的拟合精度统计

可知, 在研究区域内, 常规LSSVM建模的外符合精度为±15.4 mm, WOA-LSSVM法建模的外符合精度为±12.4 mm, 比常规LSSVM提高了19.5%, 这主要是因为鲸鱼算法在优化参数的过程中, 极大程度地避免了过早收敛或局部最优的现象, 从而提高了区域GNSS拟合模型的预测精度。

4 结束语

考虑到最小二乘支持向量机法在构建区域GNSS高程拟合模型时参数选择较为困难的问题, 本文将鲸鱼优化算法引入到最小二乘支持向量机拟合法中。WOA在参数寻优的过程中具备更高的精度及稳定性, 针对带状区域或面状区域均能够为LSSVM选择出最佳的核参数和正则化参数。采用改进后的LSSVM、 常规LSSVM及BP神经网络建模进行对比分析, 得到不同地形特征的拟合模型， 实验结果表明, 利用鲸鱼算法优化后的最小二乘支持向量机建立的高程异常拟合模型预测精度明显提高, 并且使得核函数参数和正则化参数的选择更为合理, 证明了鲸鱼优化算法建模的可行性和有效性, 为以后的测高工作提供一定的参考依据。