基于性能的既有钢筋混凝土结构抗震评估方法与应用
2021-03-24王四清艾辉军唐学武毛土明
王四清, 陈 宇, 艾辉军, 唐学武, 毛土明, 邵 磊
(1.湖南省建筑设计院集团有限公司, 长沙 410006; 2.湖南省地震局, 长沙 410004)
《中国地震动参数区划图》(GB 18306—2015)于2015年5月15日批准发布, 并于2016年6月1日实施。在第五代地震动参数区划图中, 抗震设防要求全面提高, 实现了抗震设防全覆盖, 原非抗震区的既有建筑物普遍存在抗震能力偏低, 甚至没有任何抗震构造措施的情况。这些区域内重点设防类建筑、 生命线工程建筑以及老旧保护性建筑等有提高抗震能力的切实需求。当前抗震鉴定的基本依据是2009年7月1日实施的国家标准《建筑抗震鉴定标准》(GB 50023—2009), 其设计思想是基于“小震弹性承载力+抗震延性构造措施”。随着越来越多的既有建筑都提高了对抗震能力的要求, 抗震评估和加固工作也遇到了越来越复杂的挑战, 如能直接定量评估建筑结构在中震和大震下的性能, 则可更准确判断既有建筑是否需要抗震加固及如何更有效地加固结构[1-2]。因此, 急需引入性能化设计理论, 更好地评估既有建筑的抗震性能。
1 基于性能的既有建筑抗震评估体系
基于性能的既有建筑抗震评估体系主要包括地震作用取值、 抗震性能目标、 耐久性损伤模型、 抗震分析方法等。
1.1 既有建筑地震作用取值
1.1.1 地震动的概率计算模型 根据地震概率计算均匀Poisson模型[3], 某场地在T年内发生n次烈度不低于I的地震的概率为
(1)
式中:λ(I)为烈度不低于I的地震年平均发生率。场地在T年内至少发生一次烈度不低于I的地震的概率为
PT(I)=1-PT(I, 0)=1-exp[-λ(I)·T]。
(2)
50年设计基准期内设防地震烈度的概率分布符合极值Ⅲ型分布[4]
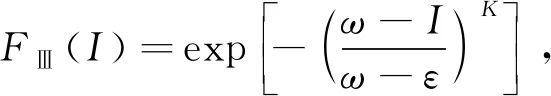
(3)
式中:ω为地震烈度上限值;ε为众值烈度;K为表示地震危险性的形状参数, 按《建筑抗震设计规范》(GB 50011—2010)取ε=I0-1.55,K在基本烈度I0分别为6、 7、 8和9度时的取值分别为9.793 2、 8.333 9、 6.871 3和5.402 8, 则任意基准期T内发生超越烈度I的地震概率为
(4)
以基本烈度I0表示, 上式可改写为
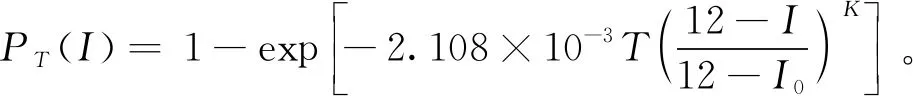
(5)
根据上式, 给定发生某一强度地震的超越概率及评估基准期, 便可计算得到既有建筑在该基准期的地震烈度I。
1.1.2 地震作用的确定原则 既有建筑结构在后续服役期内地震作用的确定可采用3种原则: 等设防烈度原则、 等超越概率原则、 等重现期原则[5]。等设防烈度原则下, 既有建筑在后续服役期内仍采用原设防烈度计算地震作用。考虑到可变荷载和结构抗力具有时变性, 等设防烈度原则夸大了结构安全需求, 会增加加固工作量。等超越概率原则下, 既有建筑在后续服役期内与原结构在设计使用年限内保持相同的超越概率。对于一般既有建筑, 基于等超越概率原则来调整地震作用的做法是最合适的, 它确保了在相同概率的前提下维持后续服役期内建筑遭遇地震风险一致。等重现期原则下, 既有建筑在后续服役期内具有原结构在设计使用年限内相同的地震重现期。对于震损建筑, 若已发生相当于设防烈度的地震, 短时间内再度发生相当设防烈度地震的概率将变小, 因此震损建筑适用采用等重现期原则确定后续使用期的地震作用。
根据等超越概率原则, 结构原设计使用年限为T年, 抗震设防烈度为I, 使用了若干年后, 使用年限调整为t年(t (6) 当K1=K2=K, 同时取上限值ω=12, 则有 (7) 上式表示的是一般既有建筑, 任意后续使用年限对应的抗震设防烈度J和原设计使用年限对应的抗震设防烈度I之间的关系。 1.1.3 后续使用年限的地震作用 根据式(7), 既有建筑不同后续使用年限的设防烈度如表1所示。地面峰值加速度A(单位Gal)与场地的地震烈度I满足统计关系[6], 即 表1 不同后续使用年限的设防烈度 A=10(I·lg 2-0.01)。 (8) 综上, 可得到既有建筑结构在不同后续使用年限评估用地震峰值加速度。将不同后续使用年限各超越概率地震动参数取值除以50年使用期下相应超越概率的取值, 就可以得到相对于50年设计使用期地震动参数的调整系数, 整理后如表2所示。 表2 不同后续使用年限的地震动参数调整系数 1.2.1 性能目标体系 既有建筑抗震设防目标在相同概率保证的前提下与新建建筑保持一致。参考国内外规范关于建筑性能目标的规定, 采用如下抗震性能目标体系[7-11]: 将性能水平分为5个等级, 如表3; 性能目标分组如表4, 其中①、 ②、 ③是既有建筑的3个组别, 它们是根据建筑的重要性划分的, 具体如表5所示。 表3 既有建筑性能水平 表4 既有建筑性能目标 表5 既有建筑分组 1.2.2 性能指标量化 结构的性能需要用力、 变形、 延性、 能量、 损伤等指标来描述。将结构性能指标分为整体性能指标和局部性能指标。整体性能指标一般由层间位移角来衡量。参考相关研究[12-13], 给出对应表3性能水平的既有钢筋混凝土框架结构和剪力墙结构层间位移角限值, 如表6所示。 表6 既有钢筋混凝土结构层间位移角限值 美国FEMA报告和ASCE 41-06标准中详细给出了各类型构件的变形性能指标, 因此基于构件变形可以判定构件的性能状态, 即确定结构的局部性能水平。 ABAQUS和SAUSAGE等软件中构件的损坏则主要以混凝土受压损伤因子和钢材(钢筋)的塑性应变程度作为评定标准。此性能评价方法是基于软件采用的材料本构模型, 并参考FEMA报告中构件性能与变形的关系逐渐发展起来的。SAUSAGE中常用的构件性能水平分级和评价标准见表7。其中, 单元各性能水平指标为下限值, 各项指标取不利; 梁柱构件性能等级取单元性能等级最大值; 墙板构件性能等级取单元按面积加权平均后的性能等级, 若中度损伤及以上单元面积占构件面积≥50%, 构件性能至少取严重损坏。当既有构件配筋不符合规范时, 其性能水平的评价指标限值应在配筋完备构件的标准上进行修正。但由于相关研究有限, 抗震构造不足的构件性能水平与混凝土受压损伤因子及钢筋塑性应变程度关系的修正一般仍靠经验进行。 表7 SAUSAGE中构件性能水平分级和评价标准 既有建筑耐久性影响因素很多, 而耐久性损伤模型的试验与理论研究还较为离散, 研究对象以锈蚀钢筋混凝土、 震损钢筋混凝土、 冻融损伤钢筋混凝土为主[14-16]。当前一般认为, 既有构件的力-位移关系(或材料本构关系)与新建建筑构件在形式上完全相同, 图1为损伤构件的骨架曲线, 其形式与完好压弯构件相同, 但相应模型参数不同。 图中,xyd、xud和xcud分别为损伤压弯构件的屈服位移、 极限位移和破坏位移,Vyd、Vud和Vcud分别为损伤压弯构件的屈服剪力、 极限剪力和破坏剪力。 图1 损伤构件的恢复力骨架曲线 因此, 在通过耐久性鉴定保证混凝土结构剩余耐久年限的前提下, 假定既有构件塑性铰力-位移关系曲线或纤维材料本构关系曲线的形式与新建建筑构件完全相同, 则可依据原设计资料和实测混凝土强度推定值、 锈损钢筋强度、 钢筋锈后面积、 构件考虑损伤后截面尺寸等确定既有结构耐久性损伤模型, 其中一般锈蚀钢筋混凝土构件可参考《既有混凝土结构耐久性评定标准》(GB/T 51355—2019)的有关规定确定上述参数值, 锈蚀受弯构件还可采用锈蚀钢筋强度利用系数和锈蚀钢筋综合应变系数考虑钢筋与混凝土粘结性能的退化影响。 结构抗震分析方法主要有线性静力分析法、线性动力分析法、非线性静力分析法和非线性动力分析法。由于多数建筑结构在中震或大震下已经进入弹塑性阶段, 因此,相关地震设防水准下的性能评估常采用非线性静力分析法和非线性动力分析法, 其中非线性动力分析法又称为弹塑性时程分析法, 可直接模拟结构在地震力作用下的非线性反应[17]。既有建筑基于性能的抗震加固设计流程如图2所示。 图2 基于性能的既有建筑抗震加固设计流程 湖南某原非抗震区学校教学楼(图3)为混凝土框架结构, 屋面标高16.8 m, 其中一层架空层高3.4 m, 其余四层层高均为4.2 m, 出屋面构架层高2.1 m。原设计混凝土强度等级为C30, 梁柱纵筋为HRB335, 箍筋为HPB235, 柱截面尺寸有300 mm×300 mm、 400 mm×400 mm, 主梁截面尺寸有250 mm×300 mm、 250 mm×400 mm、 250 mm×550 mm。教学楼典型框架结构布置如图4所示。 图3 教学楼结构整体模型 图4 教学楼典型框架结构布置 该教学楼已服役20年, 当前教学楼总体外观质量状况尚良好, 但部分框架梁梁底和个别走廊柱有锈胀裂缝,宽0.2 mm; 现场回弹法测定的混凝土强度推定值略低于原设计强度C30。本工程设计建造时未考虑抗震, 现抗震鉴定属A类与B类之间的建筑, 后续使用年限定为40年, 按《建筑抗震鉴定标准》(GB 50023—2009)核查抗震措施, 框架等级为三级(乙类建筑, 按7度采取抗震措施), 梁端箍筋直径和间距不满足要求。按《建筑抗震设计规范》对既有结构进行抗震分析, 结构构件承载力和位移角均能满足6度小震要求, 但结构平面凹凸不规则, 扭转位移比偏大, 扭转周期比大于0.9。 根据本工程特点, 对锈损梁柱剔除原受损混凝土后, 采用增大截面法(新增纵筋和箍筋)加固, 梁端箍筋不满足构造要求, 则在加密区采用外包型钢加固。考虑到原结构缺少必要的延性构造措施, 耗能能力不强, 在大震下易发生脆性破坏而危及生命安全, 在项目一定位置设置防屈曲支撑。设置防屈曲支撑的作用定位在小震下改善结构扭转特征, 大震时消能减震。防屈曲支撑类型均为耗能型, 芯材牌号均为Q235,具体参数见表8, 平面布置如图5所示。 表8 防屈曲支撑参数 图5 防屈曲支撑平面布置图 2.4.1 罕遇地震作用 综合考虑场地类别、 频谱特性、 有效峰值、 持续时间、 统计特性等方面(Ⅱ类场地、 6度、 第一组), 选择了一组人工波S01, 两组天然波S02和S03(图6), 本文仅列出主方向加速度。采用三向地震波(1∶0.85∶ 0.65)输入, 40年使用年限的大震加速度调整系数为0.94, 则主方向地震波有效峰值为117.5 Gal。 图6 大震分析地震波曲线 2.4.2 大震性能目标 根据表3~5, 学校建筑的既有建筑分组为组别②, 在大震作用下的性能水平选为满足生命安全。层间位移角限值取1/100, 耗能构件屈服耗能、 部分框架梁可到严重损坏, 一般竖向构件中度损坏为主, 关键竖向构件控制在轻度损坏以下。其中原结构框架梁梁端箍筋直径和间距不满足规范要求, 进行弹塑性分析时, 其采用的混凝土材料本构不考虑箍筋的约束效应, 且框架梁性能水平评价标准按表9修正考虑。 表9 梁端箍筋不足框架梁性能水平评价标准 综上, 基于纤维束模型, 采用SAUSAGE软件构建了既有结构的耐久性损伤模型。 2.4.4 大震性能对比 加固前, 结构扭转周期比达到了0.95, 最大位移比为1.37, 扭转效应明显; 加固后结构最大扭转周期比为0.68, 最大位移比为1.14。 如表10所示, 加固前结构在大震作用下, 层间位移角为1/69, 大于性能目标要求, 此时结构弹塑性附加阻尼比为2.1%; 加固后结构, 最大层间位移角为1/157, 满足性能目标要求, 此时耗能防屈曲支撑屈服耗能, 提供了约2.4%的阻尼比, 而结构弹塑性附加阻尼比仅0.4%。加固前结构弹塑性模型与弹性模型基底剪力的比值约0.64, 加固后该比值为0.76, 加固后结构的钢筋混凝土损伤控制得更小, 其刚度退化现象也更小。 表10 加固前后整体指标对比 如图7所示, 加固前结构在大震下, 关键竖向构件达到了重度损坏, 而同时框架梁则多为轻度损坏, 显然原结构构件的屈服顺序不合理。结构加固后, 防屈曲支撑屈服耗能使钢筋混凝土构件的损伤大幅减小, 加固后的子结构构件和关键竖向构件始终保持在轻度损坏以下, 满足性能水准要求。 图7 加固前后结构典型构件性能水平状态 本文介绍了基于性能的既有钢筋混凝土结构抗震评估与加固设计流程,并以一座已服役20年,抗震鉴定后续使用年限定为40年的框架结构教学楼加固项目为例,对比了结构加固前后的大震性能,说明给出的性能化评估与加固设计方法的可行性,得到以下结论: (1)对于一般既有建筑, 其地震作用应根据其后续使用年限进行调整。其中基于等超越概率原则来调整地震作用的做法是最合适的。 (2)对于后续使用年限少于50年的既有建筑, 在各设防水准下, 其抗震性能目标可参照新建建筑的相关规定确定; 同时, 既有建筑的性能目标体系宜能考虑其重要性分类。 (3)既有建筑经过了一定时期的服役, 由于环境和载荷作用, 结构材料会发生一定的变化、 结构构件亦会损伤, 因此既有结构的性能评估应考虑耐久性损伤。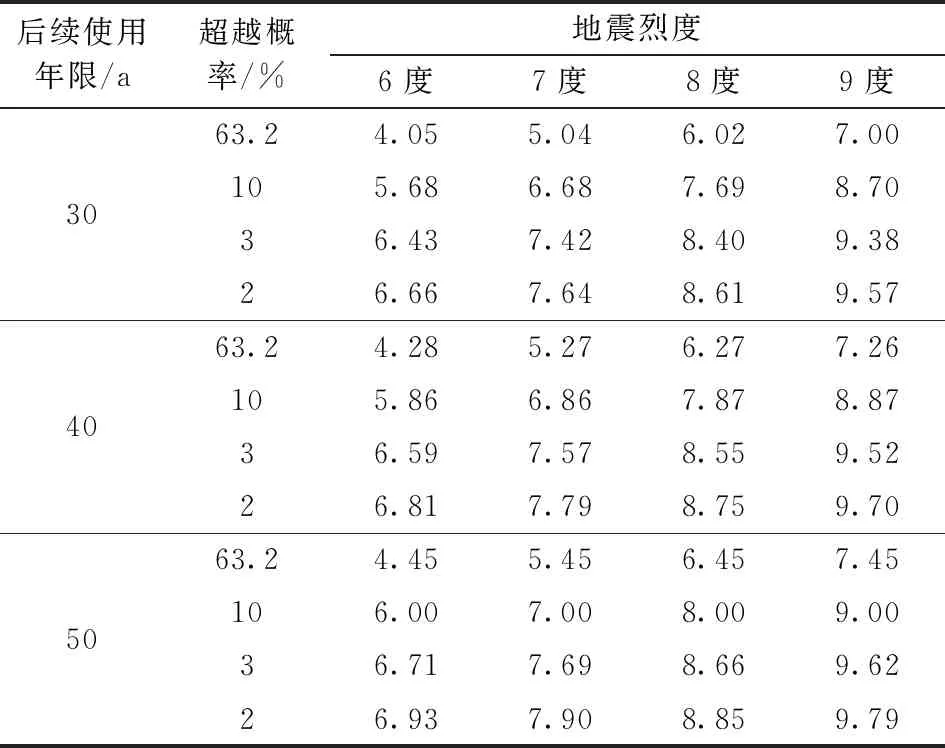

1.2 既有建筑抗震性能目标





1.3 耐久性损伤模型

1.4 抗震分析方法

2 工程实例分析
2.1 工程概况
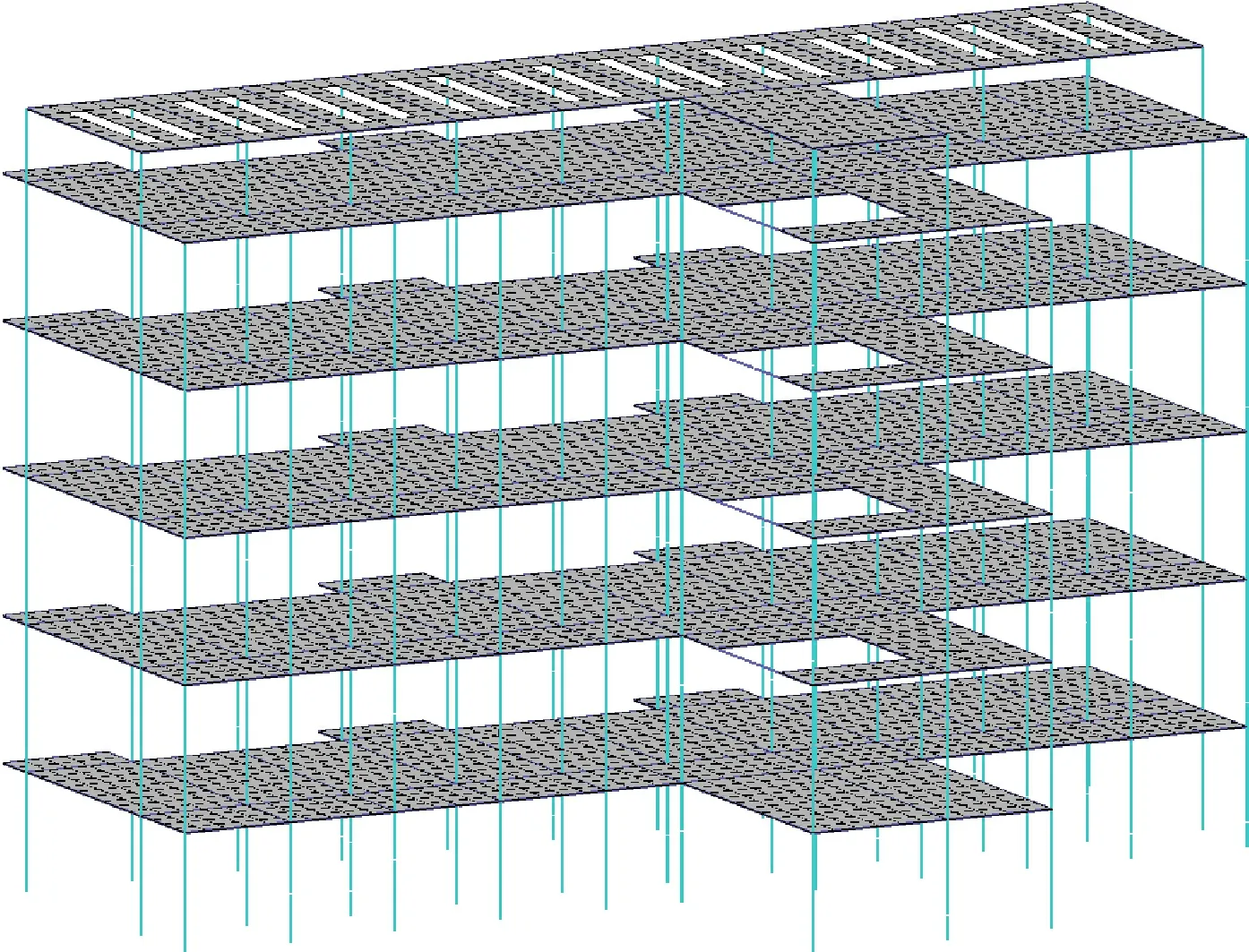
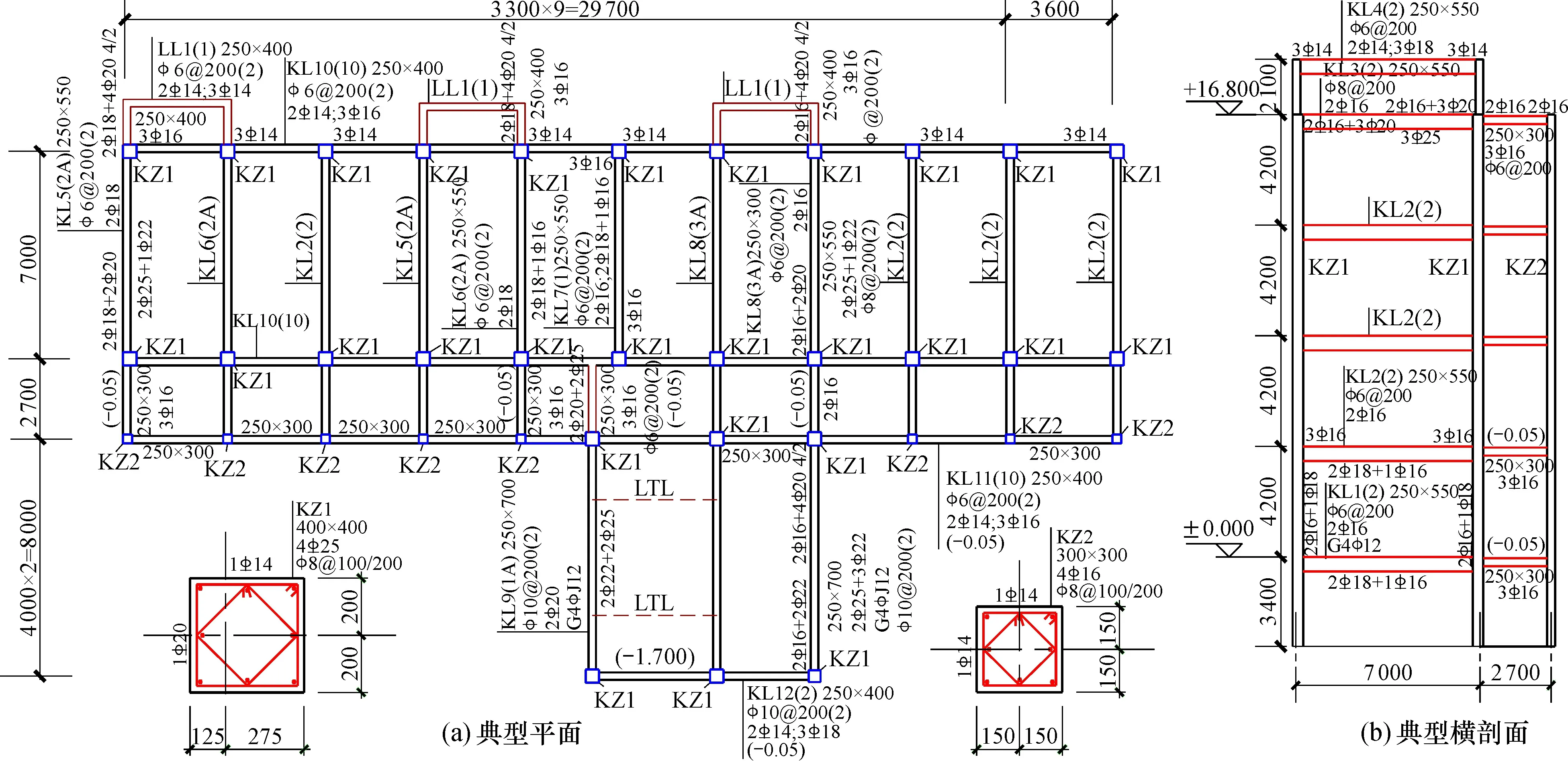
2.2 检测鉴定
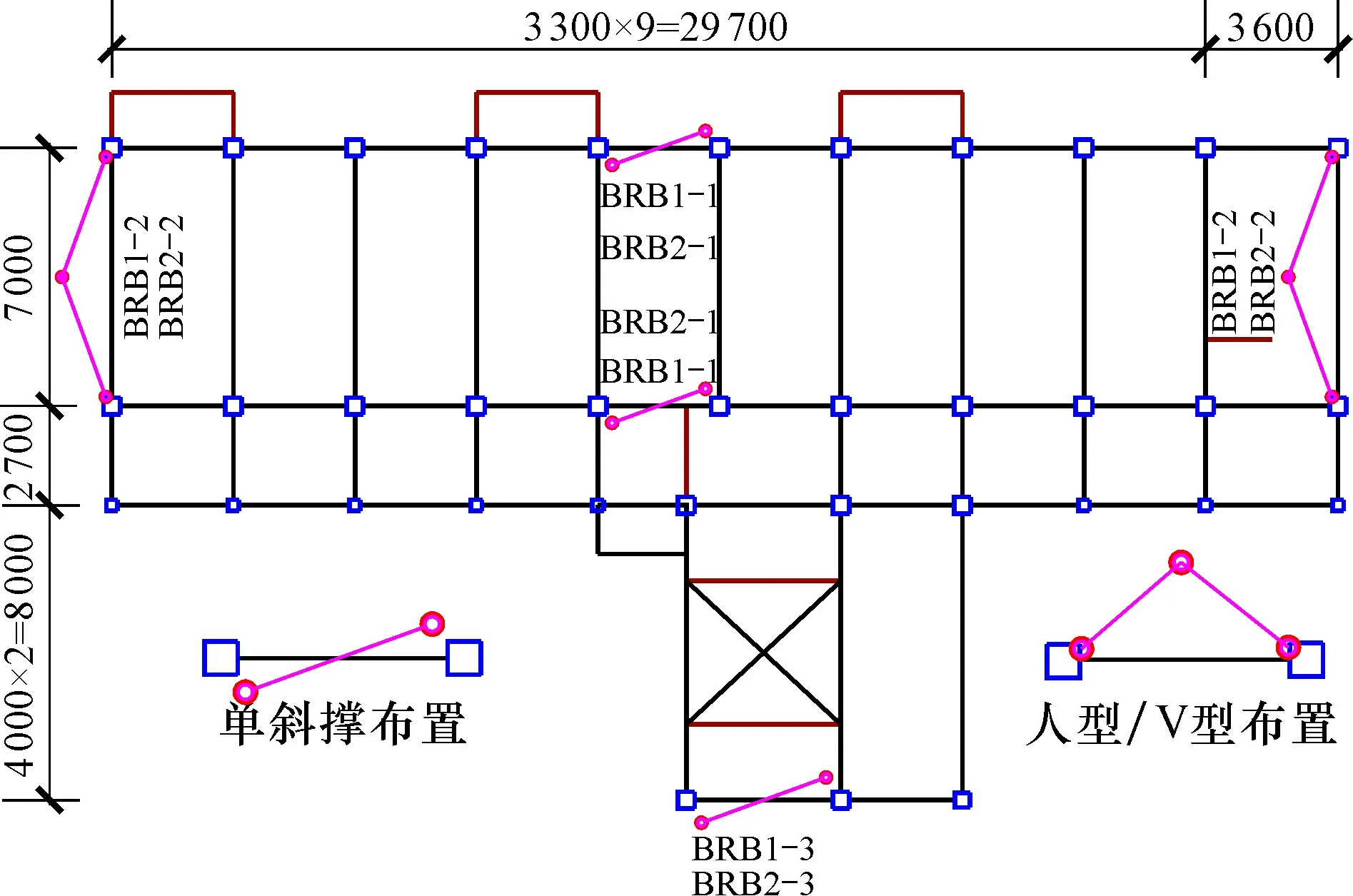
2.3 加固方案

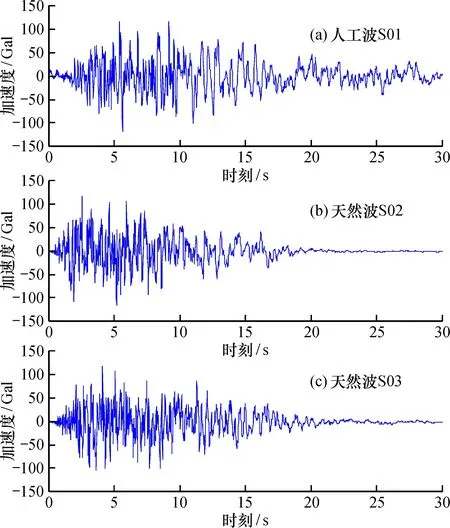
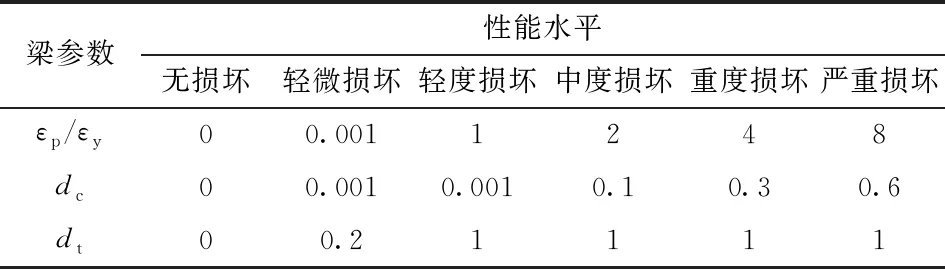
2.4 加固前后大震性能对比



3 结 论
