基于钻孔TEM智能立体成像的快速掘进超前探测方法
2021-03-24张幼振李博凡郭建磊李宇腾田小超蒋必辞
范 涛,张幼振,赵 睿,刘 磊,李博凡,郭建磊,李宇腾,田小超,蒋必辞
(1.中煤科工集团西安研究院有限公司,陕西 西安 710077; 2.陕西省重点科技创新团队(地球物理探测技术与装备创新团队),陕西 西安 710077; 3.煤炭行业工程研究中心(物探技术与装备),陕西 西安 710077)
采掘失调是煤矿安全生产的重大隐患之一,而巷道快速掘进是保障采掘平衡的重要手段[1]。煤矿井下巷道掘进需要超前预报前方的水害隐患和地质构造。据统计,近年来我国煤矿重特大事故总体呈下降趋势,但重特大水灾事故起数和死亡人数在事故占比中逐年增加,平均占比达18.05%,掘进工作面是煤矿重特大水灾事故最易发生的突水地点,占比达51.16%[2]。
目前,巷道快速掘进日进尺可达50 m以上,而矿井地球物理超前探测的有效距离仅80~100 m,探测精度受井下复杂环境影响也较低,因此探掘接续紧张矛盾已成为制约巷道掘进速度的最重要影响因素。
为了解决煤矿井下掘进工作面前方的探测深度与探测精度的矛盾,利用定向钻孔进行瞬变电磁探测工作,可以在掘进前开展远距离、高精度的隐伏水害超前预报,该方法的优势在于:① 发射回线在目标体附近激发,能在防爆限制下最大限度激发煤层附近的目标体;② 孔中接收装置则既避开了巷道中的铁磁性干扰,还能最大限度减少目标体2次场因距离带来的能量损耗;③ 通过对三分量数据的联合处理可最大程度利用单钻孔实现电阻率立体成像,提升瞬变电磁方法的解释精度,超前准确预报隐伏水体的位置和规模等空间分布信息;④ 一次性完成大于500 m超前探测,通过开钻窝接续施工可以保障快速掘进过程中不必停工等待短距离物探超前探测工作。
早在20世纪70年代,国外学者就已开展了利用钻孔瞬变电磁三分量探测信号解释孔旁地质异常的研究,WOODS等[3]进行了比例模型实验研究,总结出一套解释板体模型不同参数的特征关系曲线,MACNAE等[4]阐述了导电背景中的井中响应符号变化现象和特征,BUSELLI等[5]模拟了导电覆盖层下多个目标体的信号响应,KOZHEVNIKOV等[6]研究了钻孔套管对孔中瞬变电磁响应的影响。我国学者自20世纪80年代引入地-井瞬变电磁装备后也开展了相关研究,胡平和石中英[7]开展了基于自由空间的球体和板体的地-井瞬变电磁响应的理论计算,对国外已报导的结果进行了补充,张杰[8]推导了矩形回线在空间任意点处产生的一次场表达式,提出三分量数据矢量交汇技术,杨毅等[9]提出基于导电薄板等效涡流的异常反演方法。孟庆鑫等[10]通过大地介质影响下的正演模拟确定了围岩背景场对于总响应的影响结果,徐正玉等[11-13]采用时域有限差分法模拟研究了接触带埋深位置不同和接触面两侧电阻率不同对信号的影响,杨海燕等[14]研究了覆盖层影响下板状体异常响应规律,武军杰等[15]定义了电性源地-井瞬变电磁全域视电阻率,陈卫营等[16]对电性源在地下激发的6个电磁场分量的扩散、分布特性和探测能力进行了分析研究。在隧/巷道内工作的钻孔瞬变电磁方法近几年才被提出,相关研究资料较少,国外只有VELLA[17]曾将地-井瞬变电磁发射线圈移到金属矿巷道中来探测含金块状黄铁矿体,国内王世睿[18]研究了隧道10 m以内浅孔中的瞬变电磁响应特征,提出利用移动掘进工作面上发射线框位置来定性判断异常体方位的施工技术,孙怀凤等[19]通过物理模拟试验证明了孔中瞬变电磁信号可用于判断隧道掘进工作面前方是否存在异常构造,陈丁等[20]通过在全空间一维背景上增加三维异常体的积分方程数值模拟研究了煤矿巷道垂直孔中瞬变电磁特性,范涛[21-23]研究了钻孔瞬变电磁的叠加超前探测方法、径向探测数据的二维拟地震反演方法和短直钻孔旁裂缝的伪立体成像方法。
综合以上参考文献可知,水平分量的形态组合和幅值差异对孔旁异常体位置敏感,结合垂直分量反演成像结果可对孔旁异常进行立体解释。但是,根据水平分量异常形态组合确定异常体所在象限需人工进行识别和判断,效率较低,尤其当测点较多时,人工逐点逐测道识别异常曲线形态更是不现实的工作。因此,钻孔瞬变电磁法当前的立体解释还处于定性水平,有必要引入机器学习中的聚类算法实现智能识别水平分量异常形态。
聚类算法在地震勘探领域应用较多,刁桂苓等[24]利用系统聚类对海城地震序列中的24个震源机制解进行了聚类分析,王伟涛和王宝善[25]基于层次聚类分析有效识别了汶川余震序列中的相似地震以及重复地震,张岩等[26]应用结构聚类字典学习有效压制了地震数据随机噪声;在重磁资料的处理解释中,张新兵等[27]提出了一种基于改进K-means聚类分析的重磁局部异常自动圈定方法,李斐等[28]基于聚类分析结果来优化重力数据在不同区域的观测密度,曹书锦等[29]引入自适应模糊聚类算法实现了准确确定多异常源;而在电磁数据处理解释领域,在大地电磁方法中聚类分析应用相对较多,杨生和杨彦峰[30]将其用于大地电磁曲线分类中,有效克服地质推断的多解性,李晋等[31]提出基于递归分析和聚类的信噪比辨识及分离算法,改善了低频段的MT数据质量,黄颖等[32]使用K-means聚类对MT三维反演结果中的地质构造进行了识别和归类。
参考以上资料,笔者通过机器学习中的聚类算法对大数据量水平分量异常响应曲线形态进行自动分类,完成异常空间角度定位,并建立其与反演深度的映射关系,最终实现钻孔瞬变电磁立体成像解释。

图1 模型示意Fig.1 Schematic diagram of the mode
1 孔旁异常体定位基本原理
1.1 不同象限异常体的水平分量特征
设计如图1所示模型,发射线圈中心法线方向与钻孔延伸方向(Z方向)一致,接收线圈中心法线方向与X,Y,Z正方向一致。规定X分量与Y分量正方向之间区域为第1象限,顺时依次定义为2,3,4象限,在Z=50 m处,分别放置16个规模为20 m×20 m×6 m的水平长方异常体,异常体中心点组成的正方形边长为30 m,模型中煤层、巷道和异常体的电阻率分别为1 000,10 000,10 Ω·m。采用文献[23]中的方法提取水平分量异常后,绘制16个长方体的水平分量异常响应多测道图如图2所示,图中横坐标h为钻孔深度。
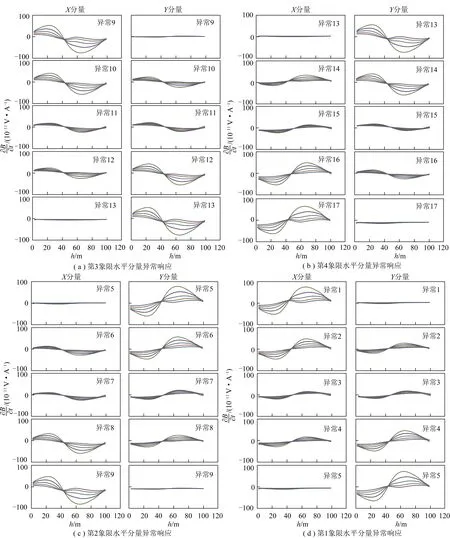
图2 模型的水平分量异常响应Fig.2 Horizontal component response of the model
由图2可知,以水平钻孔为参考系,所有水平分量异常响应形态均为“正弦曲线”或“反向正弦曲线”形态,且当异常中心与钻孔的连线与坐标轴夹角为0°时,与该坐标轴方向对应的水平分量的响应幅值达到最小。两组水平分量形态组合与异常体所在象限之间的关系如图3所示。

图3 异常位于不同象限时水平分量响应形态Fig.3 Horizontal component response curve in different quadrant
1.2 异常体XOY平面旋转角计算方法
钻孔瞬变电磁径向探测时,异常体引起的二次场是矢量场,那么由水平涡流场的空间分布特征可知,在钻孔中观测到两个水平分量Vx,Vy的矢量和Vxy,其方向一定是由钻孔指向异常体的等效涡流中心上,那么只需要求出Vxy的方向,就知道异常体中心的具体方位。
如图4所示,设Vxy与X轴夹角为θ,则
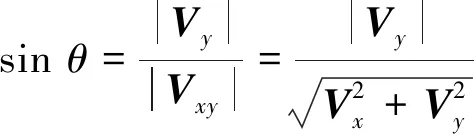
(1)
其中,Vx,Vy均为已知值,求反正弦即得到
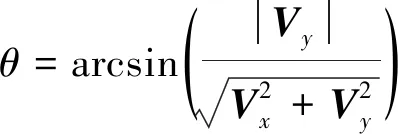
(2)

图4 异常偏转角示意Fig.4 Schematic diagram of abnormal deflection angle window
最后根据异常体所在象限,可由如下公式求出对应的XOY平面旋转角α:① 异常体在第1象限:α=θ;② 异常体在第2象限:α=π-θ;③ 异常体在第3象限:α=π+θ;④ 异常体在第4象限:α=2π-θ。
根据以上内容,可以看出,若将钻孔旁空间中任意一点都视为一个小的地质异常体,理论上可以对任意一点的电阻率进行空间定位,实现孔旁电性信息立体成像。但显然,水平分量异常场形态的确定工作量很大,依靠人工完成难以保证效率,必须引入人工智能算法实现曲线形态自动分类。
2 孔旁异常体智能立体成像方法
2.1 水平分量异常曲线类型自动识别方法
欲对水平分量异常场曲线进行自动分类,应以每一个测点为插值窗口中心,采用Hermit插值求得所有窗口对应的水平分量异常场。插值窗口大小的选择可根据垂直分量中的主要异常区统计平均值确定。之后对提取出的异常数据进行正规化,将曲线横坐标范围统一,然后对区间正规化后的所有异常数据进行特征提取,提出数据中极值对应的正规化点号,最后以极大值点号为X轴,极小值点号为Y轴,形成特征值分布图(图5)。
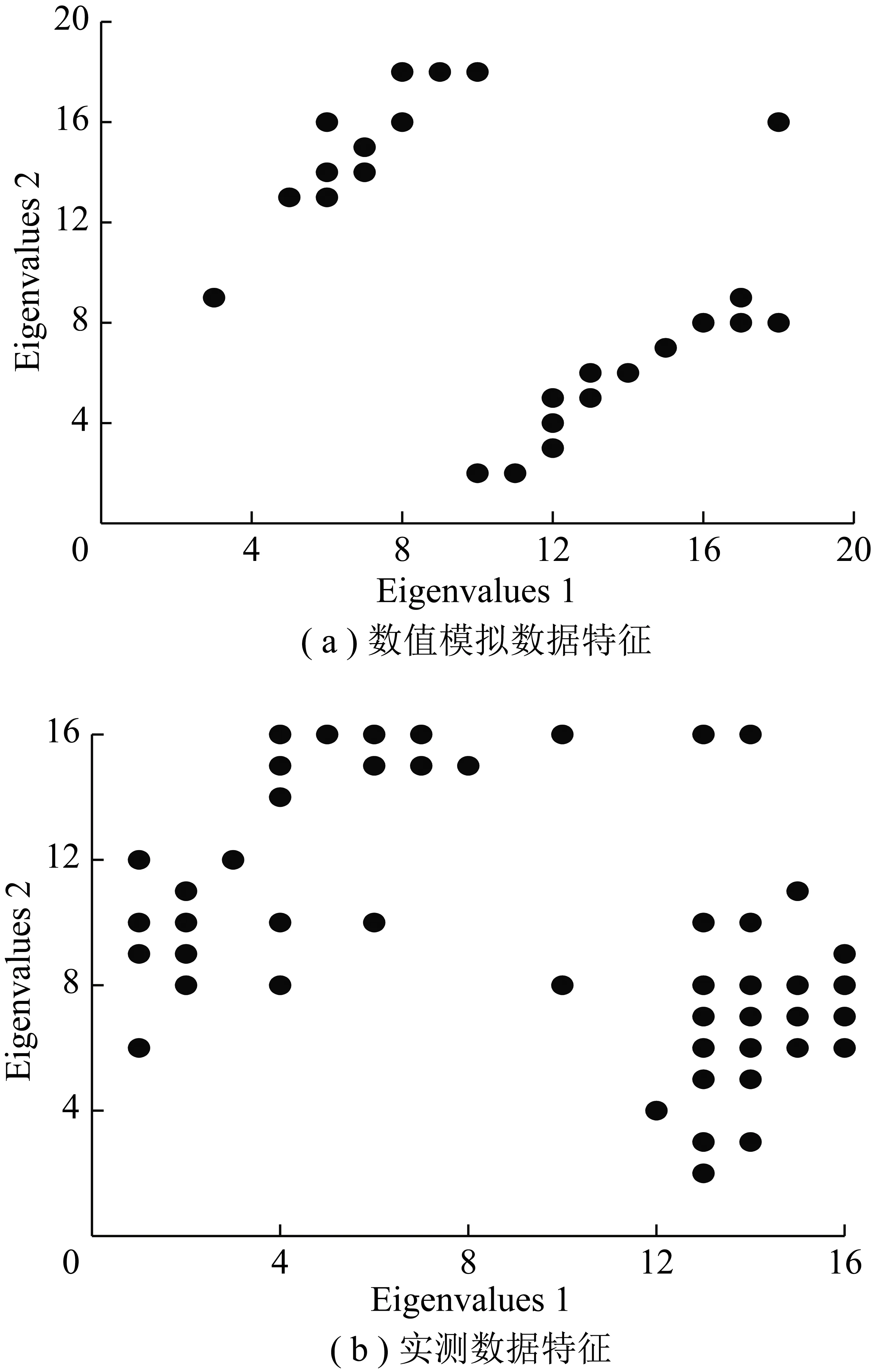
图5 特征值分布Fig.5 Distribution of eigenvalues
图5为1组数值模拟数据和1组实测数据的水平分量异常场特征值分布,可以看出均具有明显的二分类特性,与水平分量异常场的“正弦曲线”或“反向正弦曲线”形态存在显著相关性。基于该特性,无需提前进行标签样本的监督训练,可直接选用无监督机器学习算法对数据进行分类。
无监督机器学习常常被应用在数据挖掘领域,用于在大量无标签数据中发现规律。它的训练数据是无标签的,训练目标是能对观察值进行分类或区分等。常用的无监督学习算法主要有主成分分析方法、等距映射方法、局部线性嵌入方法、拉普拉斯特征映射方法、黑塞局部线性嵌入方法、局部切空间排列方法和最常用的聚类方法。
聚类算法是指将一堆没有标签的数据自动划分成几类的方法,这个方法要保证同一类的数据有相似的特征。笔者选择K-means聚类算法,该算法是使用最大期望算法求解的高斯混合模型在正态分布的协方差为单位矩阵,且隐变量的后验分布为一组狄拉克δ函数时所得到的特例,它假设相同类别中数据之间的距离应该都很近,即数据之间的相似度与它们之间的欧式距离成反比。
需要将n个水平分量纯异常数据{xk}聚为2类,令经过聚类之后每个数据所属的类别为{tk},而这2个聚类的中心为{μl},可定义如下的损失函数L:
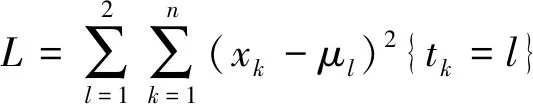
(3)
式中,l为聚类数目。
实际计算时先随机设置2个质心把所有数据粗略分成2个初始类,计算所有数据与质心的欧式距离,再根据平均值重新计算质心和类别,对以上过程反复迭代,直至达到终止条件。终止条件可设置为簇中心点变化率ηk,即
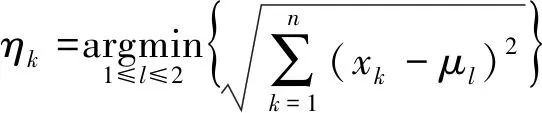
(4)
将分类好的数据类别与“正弦曲线”或“反向正弦曲线”形态进行对应,根据图3就可以准确确定钻孔瞬变电磁观测数据中任意测点任意测道反映的电性信息所在的象限,再按照第1.2节所述的异常体XOY平面旋转角计算方法,将每一测点每一测道对应的电性信息视为异常体代入计算,即可获取对应的XOY平面旋转角度。
2.2 垂直分量一维反演深度与XOY平面旋转角的映射
得到每一测点每一测道的XOY平面旋转角后,就需要求取相应的反演电性信息。笔者使用的钻孔瞬变电磁工作方法本质上仍属于中心回线装置类型,其垂直分量实测数据曲线形态与矿井瞬变电磁探测数据曲线形态基本相同(图6),仅是因为发射线圈尺寸与匝数的原因而导致电感影响较大,因此数据处理方法可参考矿井瞬变电磁,采用文献[33]中的预处理技术对电感影响进行校正,对校正后的数据则可应用Occam反演、虚拟波场反演等方法[34-35]进行深度和电阻率反演。

图6 矿井装置与钻孔装置实测曲线对比Fig.6 Comparison of measured curves between mine device and borehole device
但因为反演得到的地层层数一般远小于观测时间道数,因此由垂直分量反演得到的深度(钻孔探测半径)与采样时间之间并不存在一一对应关系,而计算得到的XOY平面旋转角与采样时间一一对应,因此无法直接形成反演深度与XOY平面旋转角的映射,限制了反演电阻率的立体化。
为解决这一问题,首先引入瞬变电磁生产中经常使用的基于趋肤深度原理的深度计算公式

(5)
式中,h为反演得到的深度(钻孔探测半径);C为深度系数;ρ为反演得到的电阻率;t为采样时间。
根据式(5),计算大量层状模型,并对比不同电阻率参数情况下的层状模型分界面的计算深度与模型设定深度之间的差别,推导出深度系数C与电阻率ρ的关系如图7所示。

图7 深度系数与电阻率的关系Fig.7 Relationship between depth coefficient and resistivity
可以看出,在对数坐标系下,深度系数与电阻率呈现线性关系,通过拟合可以得到该直线方程为
lgC=-0.500 093 65lgρ-0.001 374 49
(6)
由式(6)可逐层推导出层状地层情况下反演深度与采样时间之间的计算公式,建立2者之间的映射关系,进而建立反演钻孔探测半径与XOY平面旋转角的一一对应关系,具体算法如下:
(2)根据lgC=-0.500 093 65lgρ-0.001 374 49计算第i层对应的标准系数Ci;
(3)根据Ai=lgCi-lgC1,CRi=10Ai计算第i层对应的相对系数CRi;
(4)除第1层外的第i层真深度与采样时间可建立:
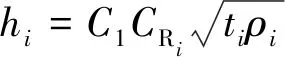
(7)
即在第1层外的第i层的采样时间可以按如下公式计算:
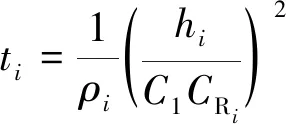
(8)
此时由反演得到的深度(钻孔探测半径)和电阻率可反推出相应的采样时间,再通过插值可以获得与实际采样时间道对应的反演钻孔探测半径和电阻率。
2.3 反演结果的立体成像算法
由钻孔瞬变电磁探测的垂直分量可反演得到以钻孔孔深为横坐标、以钻孔探测半径为纵坐标的一维反演电阻率剖面成像图,在已求得图中每一测点每一测道电性信息对应的XOY平面旋转角信息时,假设钻孔为直钻孔,可通过三角函数关系将其投影在XY平面上,将剖面图中每一测点的一维反演电性信息曲线转换为二维电性信息平面,多个测点的二维成像结果组合即可实现钻孔瞬变电磁反演电阻率立体成像。
单个测点电性信息一维坐标扩展至二维的计算公式为
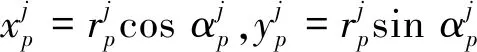
(9)
式中,j为测点数;p为测道数;x为钻孔瞬变电磁坐标系中电性信息对应的X方向坐标;y为钻孔瞬变电磁坐标系中电性信息对应的Y方向坐标;r为钻孔探测半径;α为XOY平面旋转角。
2.4 非直钻孔立体成像成果空间坐标校正方法
由于施工空间为定向长钻孔,其真实轨迹并非直线,有必要根据钻孔轨迹对基于直线钻孔坐标系的电阻率立体成像的空间坐标进行校正,获取与实际空间位置完全对应的立体成像成果。
首先要计算钻孔轨迹,实际的钻孔轨迹是一条空间曲线,计算钻孔轨迹坐标时假设钻孔轨迹由若干直线段组成,得到每个测段的坐标增量,然后累加求得坐标值进行轨迹绘制。
以计算第2测量点坐标为例说明:测量起始位置处为原点(X1=0,Y1=0,Z1=0),第2测量点各坐标增量(ΔX1,ΔY1,ΔZ1)可表示为
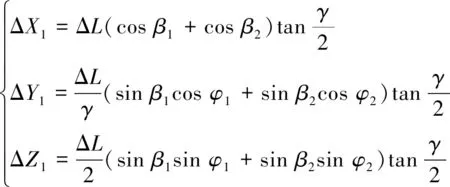
(10)
γ=arccos[cosβ1cosβ2+sinβ1sinβ2cos(φ2-φ1)]
(11)
式中,ΔL为测点间距;β1为第1测量段倾斜角;β2为第2测量段倾斜角;φ1为第1测量段倾斜方位角;φ2为第2测量段倾斜方位角。
即第2个测量点处钻孔轨迹坐标为
X2=X1+ΔX1,Y2=Y1+ΔY1,Z2=Z1+ΔZ1
(12)
要进一步实现三维探测成果的空间展示,还需要对探测成果坐标系进行三维转换。以钻孔轨迹为旋转轴,以测点所在孔位的倾角和方位角为旋转角进行空间旋转。新、原坐标系相对位置如图8所示,新坐标系原点坐标为(X0,Y0,Z0),相对原坐标系其单位坐标矢量关系为

(13)
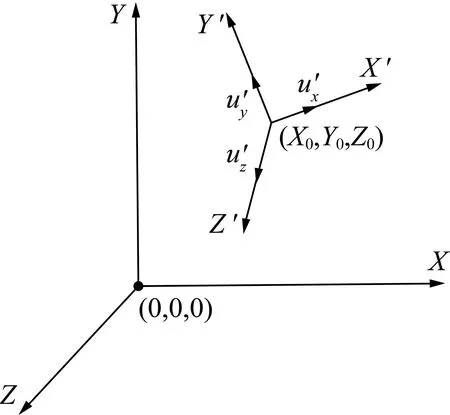
图8 新、原坐标系相对关系Fig.8 Relative relationship between the new and original coordinate systems
因此,要将三维坐标从原XYZ坐标系转换成新X′Y′Z′坐标系,可由以下两步实现:
步骤1:平移矩阵。
平移矩阵T可表示为
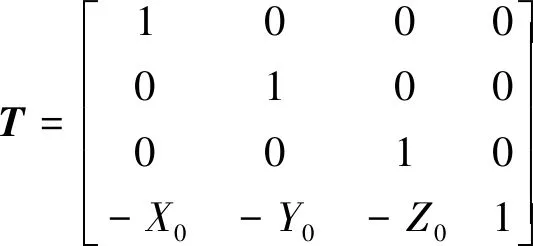
(14)
步骤2:构造坐标旋转矩阵。
坐标旋转矩阵R可表示为

(15)
其坐标变换可用矩阵表示为
(X′,Y′,Z′,1)=(X,Y,Z,1)·T·(-X0,
-Y0,-Z0)·R
(16)
对已得出的直线钻孔坐标系下的成像结果中每一点空间坐标都进行如上变换,即可实现与实际钻孔轨迹对应的电阻率立体成像处理。
3 模拟检验
3.1 数值模拟
为验证基于水平分量异常特征聚类的钻孔瞬变电磁立体成像方法探测效果,设计如图9所示的三维模型,采用时域有限差分方法进行了数值模拟。在钻孔深度方向50 m处,第3象限偏转30°放置1个规模为15 m×15 m×15 m的低阻异常体,异常体中心点距离钻孔30 m,模型中煤层、巷道和异常体的电阻率分别为1 000,10 000,10 Ω·m。
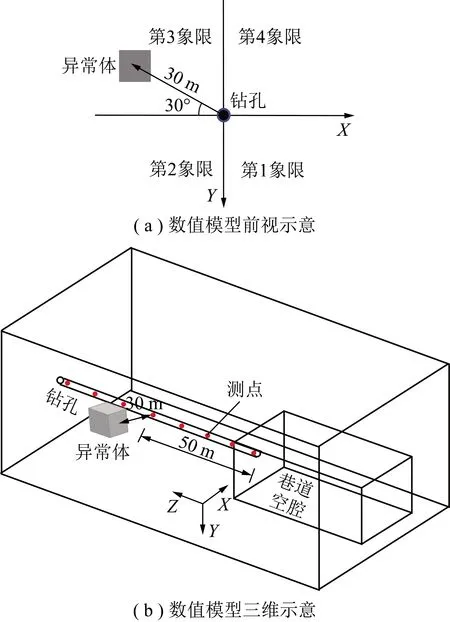
图9 数值模型示意Fig.9 Schematic diagram of the mode
对钻孔深度20~80 m内的测点数据进行Occam反演成像可得到如图10所示的沿钻孔方向的电阻率剖面,由图10可知在钻孔深度Z=50 m、钻孔径向R=20~30 m位置有较为明显的低阻异常响应,但从图10中无法反映异常的空间方位。
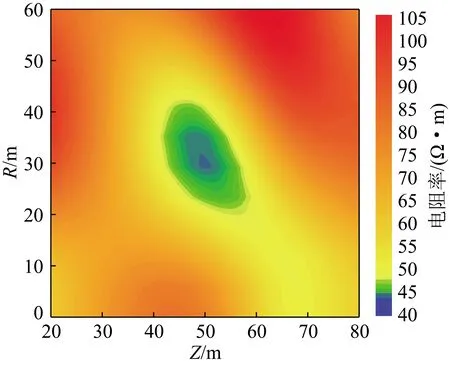
图10 数值模型电阻率剖面Fig.10 Resistivity profile of numerical model
采用本文1.2和2.1节方法对模型水平分量进行处理,再采用2.2和2.3节方法对反演电阻率进行XOY平面旋转角分配,可得到如图11所示的单测点电阻率展开平面图。由图11可以看出,在孔深50 m的平面图中XY平面第3象限有明显的低阻异常响应,其中心点与坐标系原点(钻孔)之间的距离为30 m,形状规模与模型参数基本一致,而在孔深20 m和70 m的平面图中则没有明显低阻异常显示。

图11 单测点电阻率展开平面Fig.11 Expanded plan view of resistivity of single measuring point
将每一测点的X,Y坐标与钻孔孔深Z坐标组合,通过Voxler软件进行立体成像如图12所示。图中低阻异常体与模型设置参数一致,说明基于水平分量异常特征聚类的方法对钻孔径向电阻率立体成像有效,准确性较高。
3.2 物理模拟
为进一步验证立体成像方法对钻孔瞬变电磁实际数据的探测效果,在长安大学地球物理专用的物理模拟实验水槽进行了模拟试验,模型设置参考数值模型,如图13所示,模型介质水和铜板的电阻率分别为40,1.75×10-8Ω·m。采用多匝小线框激发、多匝小线框接收的施工方式取得数据,发射线圈边长为0.4 m,匝数为10匝,接收线圈面积约为0.9 m2,发射电流强度为1.5 A,施工布置如图13所示,测线上有15个测点,测点间距为0.05 m。在模拟钻孔深度方向0.35 m处,第3象限偏转30°放置1个规模为0.2 m×0.2 m×0.002 m的铜板,铜板边界距离钻孔0.1 m。
对模拟钻孔深度0~0.7 m的测点数据进行Occam反演成像可以得到如图14所示的沿模拟钻孔方向的电阻率剖面图,可以较为清晰的看到在钻孔深度Z为0.35 m、钻孔径向R为0.1~0.3 m位置有较为明显的低阻异常响应,但从该成果图中无法反映异常的空间方位。
采用本文1.2和2.1节方法对模型水平分量进行处理,再采用2.2和2.3节方法对反演电阻率进行XOY平面旋转角分配,可得到如图15所示的单测点电阻率展开平面图。由图15可看出,在孔深0.35 m的平面图中XY平面第3象限有明显的低阻异常响应,其边界与坐标系原点(钻孔)之间的距离为0.1 m,形状规模与铜板参数基本一致,而在孔深0.15 m和0.55 m的平面图中则没有明显低阻异常显示。
将每一测点的X,Y坐标与模拟钻孔孔深Z坐标组合,通过Voxler软件进行立体成像如图16所示。
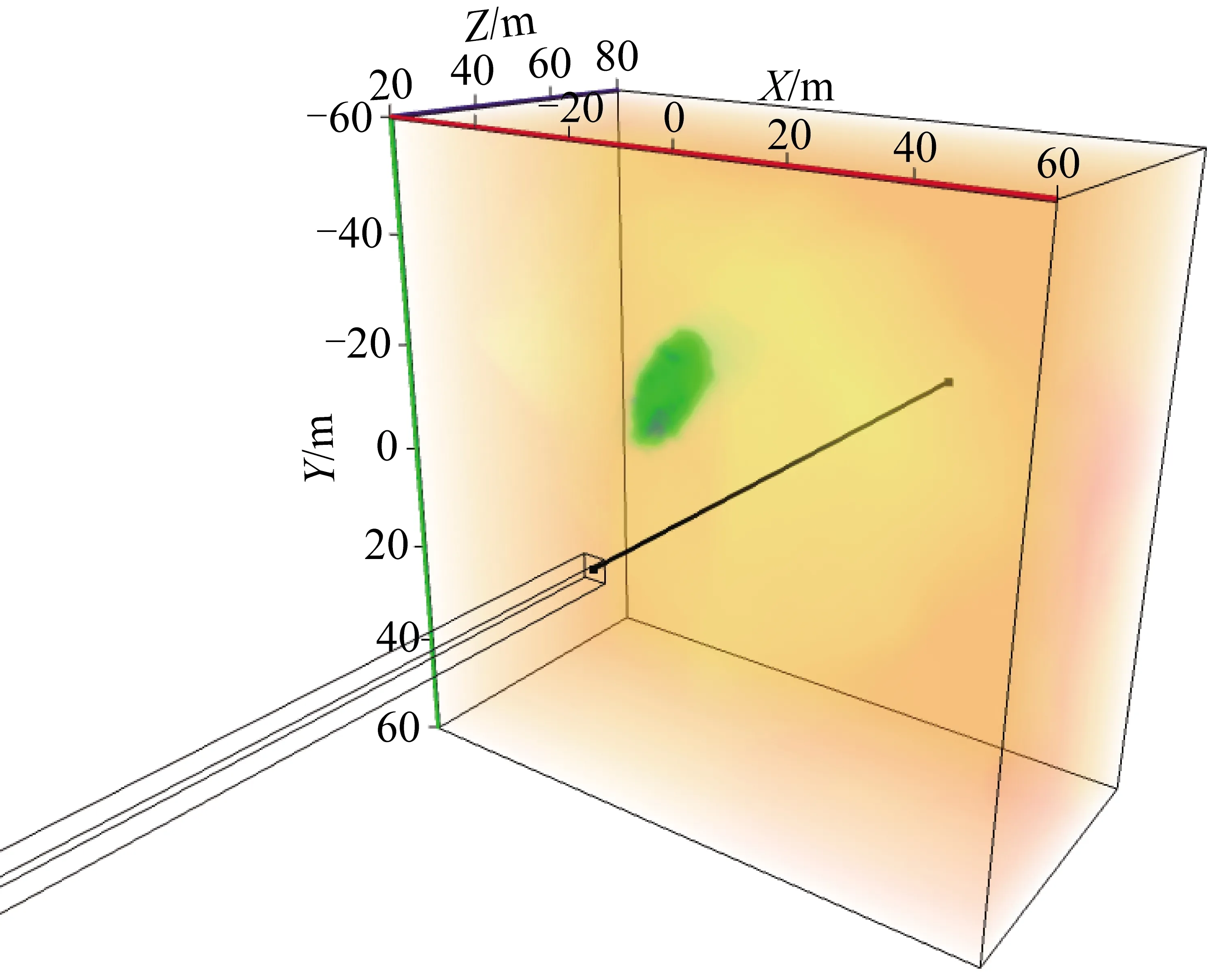
图12 电阻率立体成像图Fig.12 Stereo imaging diagram of resistivity
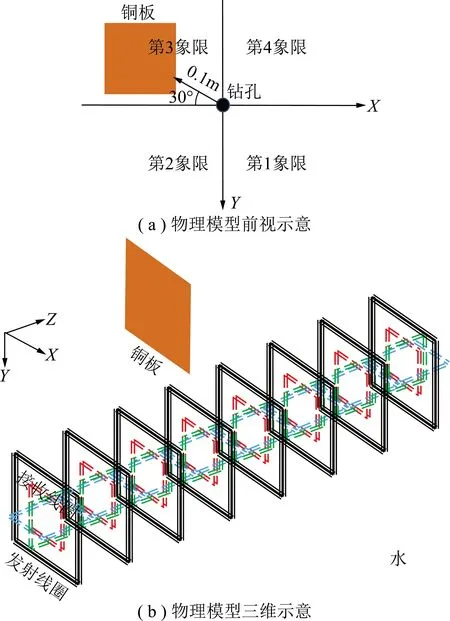
图13 模型施工示意Fig.13 Schematic diagram of the model

图14 物理模型电阻率剖面Fig.14 Resistivity profile of physical model
图中低阻异常体与铜板参数基本一致,说明立体成像方法对钻孔瞬变电磁实际数据同样有效,准确性较高。
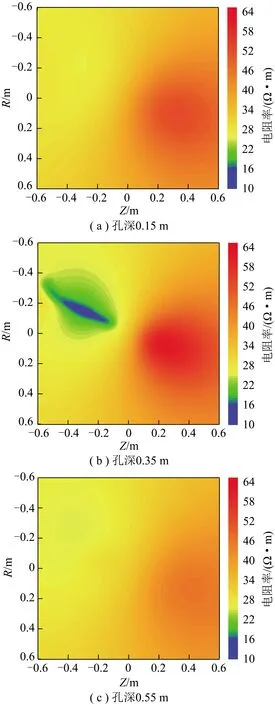
图15 单测点电阻率展开平面Fig.15 Expanded plan view of resistivity of single measuring point
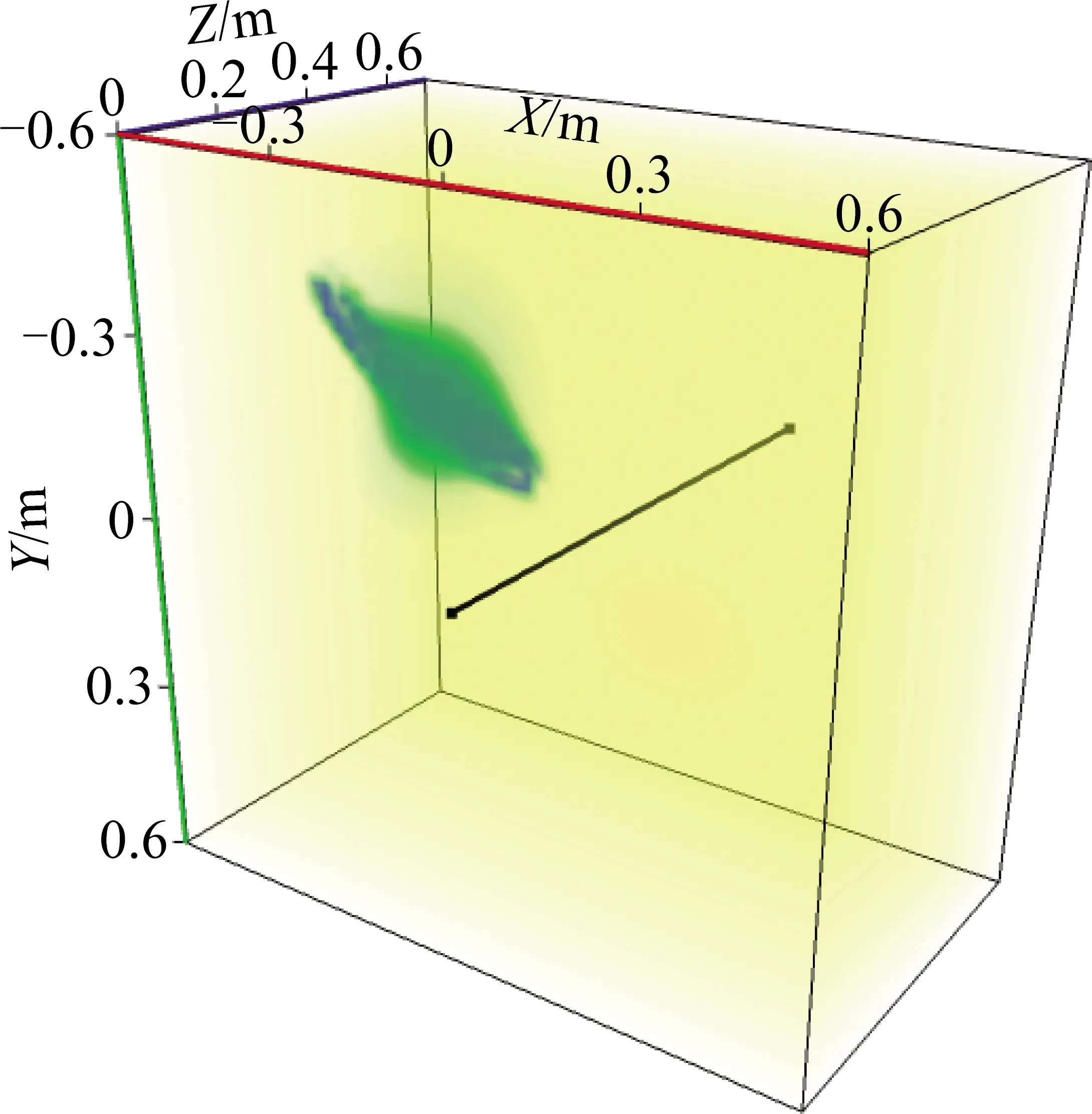
图16 电阻率立体成像Fig.16 Stereo imaging diagram of resistivity
4 探测实例
山西某煤矿所处井田地质构造复杂,已开采工作面内部陷落柱分布密集,为了保障03工作面回风巷掘进效率,在巷道开拓前采用定向钻孔中瞬变电磁技术对掘进巷道遭遇构造情况进行长距离超前探查。
钻场位于03工作面回风联络巷,偏离03工作面回风巷17.7 m,开孔位置上距03号煤底板4.5 m,下距02号煤顶板1.38 m,钻孔深度468 m。根据已知地质信息,两层煤中间夹层主要是砂岩和泥岩。钻孔瞬变电磁施工段为孔深12~450 m,测量点距为3 m,具体如图17所示。
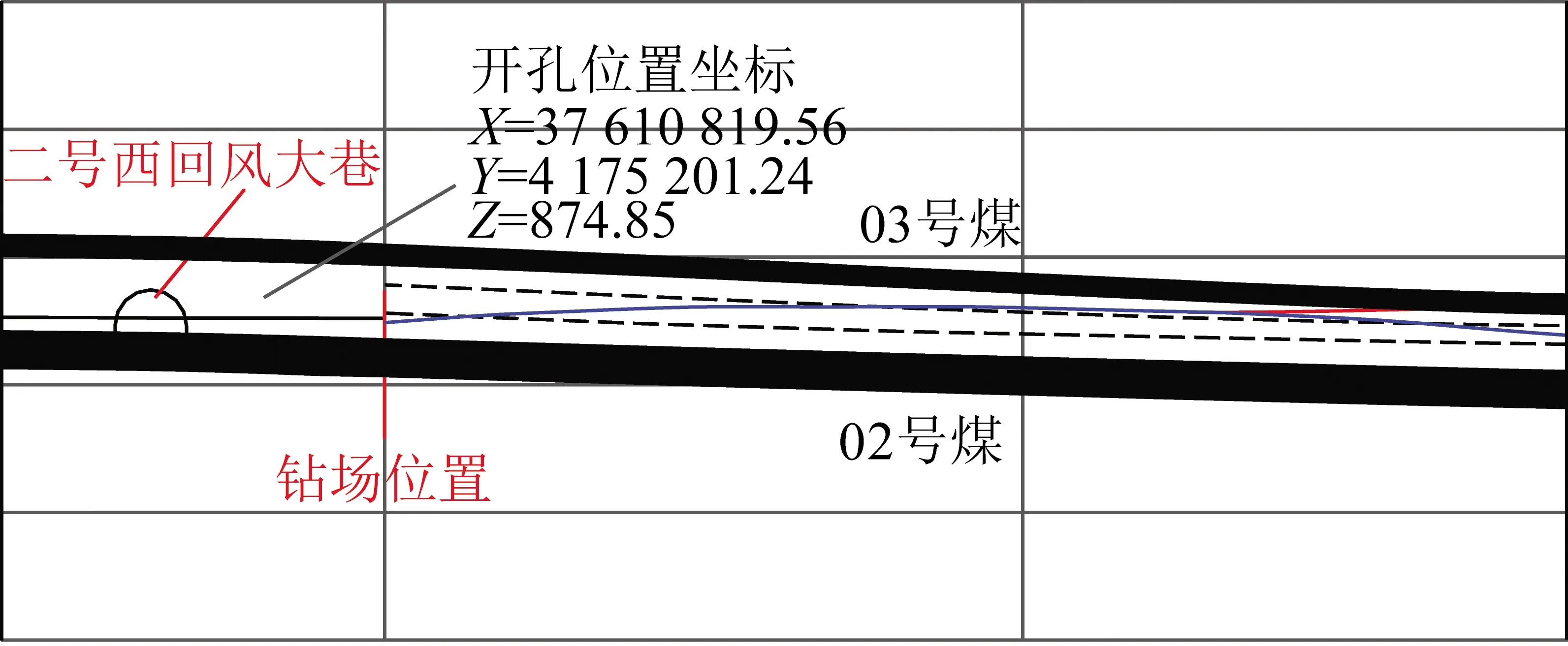
图17 03工作面定向钻孔开孔位置剖面Fig.17 Sectional view of the position of the directional drilling hole in 03 working face
对钻孔内的测点数据进行Occam反演成像可以得到如图18所示的沿钻孔方向的电阻率剖面图,可以较为清晰的看到在钻孔深度Z为380~450 m、钻孔径向R为2~20 m位置有较为明显的低阻异常响应,但从该成果图中无法反映异常的空间方位。
采用本文1.2和2.1节方法对实测数据水平分量进行处理,再采用2.2,2.3和2.4节方法对反演电阻率进行XOY平面旋转角分配和空间坐标校正,可得到如图19所示的单测点电阻率展开平面图。由图19可以看出,在孔深432 m的平面图中XY平面下方两个象限均有明显的低阻异常响应,且在中部有一笋状突起,而在孔深300 m的平面图中则没有明显低阻异常显示。
将每一测点的X,Y坐标与钻孔孔深Z坐标组合,通过Voxler软件进行立体成像如图20所示。图中低阻异常体主要分布在钻孔深度380~450 m,钻孔下方2~20 m位置,在该区域,钻孔自然伽马测量值同样跳动较大,且钻孔施工至433 m时返渣中出现黄色物质,该物质未在之前钻探砂岩返渣中出现,因此综合推测此处可能存在陷落柱构造。

图18 实测数据电阻率剖面Fig.18 Resistivity profile of measured data

图19 单测点电阻率展开平面Fig.19 Expanded plan view of resistivity of single measuring point
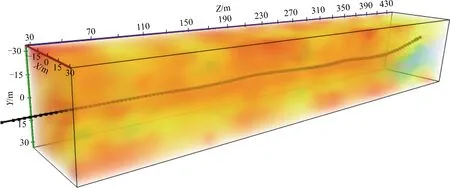
图20 电阻率立体成像Fig.20 Stereo imaging diagram of resistivity
根据本次物探工作结果,矿方立即对该疑似陷落柱做了工作预案,并开展快速掘进工作。可见,基于定向钻孔的瞬变电磁立体成像方法为矿方安全快速掘进提供了远距离地质超前预报方面的有力技术支撑。
5 结 论
(1)以钻孔钻进方向为Z轴正方向,以孔口所在平面右向为X轴正方向,下向为Y轴正方向,钻孔瞬变电磁所有水平分量异常响应形态均为“正弦曲线”或“反向正弦曲线”形态,且当某一水平分量与该水平分量坐标轴夹角为0°时,该水平分量的响应幅值达到最小,因此,通过X,Y分量异常形态组合可判定异常体所在象限。
(2)由2组水平分量的幅值基于三角函数关系可计算得到异常体中心在异常所在象限内的偏转角度,结合异常象限可得出异常体中心XOY平面旋转角。
(3)在对数坐标系下,深度计算系数与电阻率呈线性关系,因此借由深度经验公式可推导出深度-电阻率与采样时间的映射关系,实现反演电阻率与测点测道的一一对应。
(4)将测量数据每一测点每一测道对应的电阻率视为一个独立的异常体,采用K-means聚类算法对相应的两组水平分量异常曲线中的极值进行二分类,可以自动确定任意一点一道电阻率的分布象限,再由水平分量异常场幅值算出XOY平面旋转角,即可结合垂直分量成像结果实现钻孔径向电阻率的立体成像。
(5)假设钻孔轨迹由若干直线段组成,根据每个测段的坐标增量累加可求得坐标值得出定向钻孔轨迹,再以该轨迹为旋转轴,以异常位置角度为旋转角进行空间旋转,可实现非直钻孔径向的电阻率立体成像。
(6)数值模拟和物理模拟对本文提出的方法做了充分的检验,反演结果与模型吻合度较高,说明该方法准确、有效,提高了钻孔瞬变电磁方法的解释水平。
(7)井下巷道空间内的探测实例通过立体成像远距离超前预报了一个威胁矿方安全生产、影响矿方巷道掘进的陷落柱,并获得了钻孔自然伽马测井资料和钻探返渣的佐证,证明本文方法可以推广应用至煤矿实际生产中,为掘进前工作面前方500 m距离内隐伏水害远距离精准超前探测提供技术支撑,进一步通过接续钻进+探测可有效保障巷道快速掘进。
