黏弹TI煤层介质3层模型Love槽波频散与衰减特征
2021-03-24姬广忠吴荣新张平松郭立全胡泽安焦文杰
姬广忠,吴荣新,张平松,郭立全,胡泽安,焦文杰
(1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001; 2.安徽理工大学 矿山地质灾害防治与环境保护安徽普通高校重点实验室,安徽 淮南 232001; 3.安徽理工大学 地球与环境学院,安徽 淮南 232001)
煤层内断层、陷落柱等构造严重危害煤矿安全开采。槽波方法[1-2]在探测构造方面具有较好效果[3]。
煤层是由有机物质和无机物质组成的层状沉积岩体,质地相对围岩较软,具有较强的黏弹性[4-6]。煤层横波品质因子大多在30~60[1],对槽波能量吸收较大。程久龙等[7]研究了黏弹性介质3层模型的Love波传播特性,指出煤层Q值随频率变化,在Airy相附近急剧减小,槽波衰减增大,需要进行衰减补偿。LI等[8]估算了与频率相关的Love槽波品质因子值,YANG等[9]计算了3层黏弹介质Rayleigh槽波衰减曲线,LI等[10-11]利用有限差分模拟研究了黏弹介质中的槽波以及起伏巷道中的槽波传播情况。
煤层层理结构明显,构造煤裂隙较为发育,煤层介质具有显著的各向异性[12-14]。不同地区的煤既有弱各向异性,也有中等甚至强各向异性[15-18],比较复杂多样。BUCHANAN等[19]从群速度频散曲线测得的煤层不同方向速度差异高达14%。LIU等[20]计算了二维模型EDA(Extensive Dilatancy Anisotropy)介质中的槽波,发现理论合成记录和实际结果在旅行时间、振幅和频散特征等方面吻合较好。DRESEN等[1]指出只有充分了解不同方向的速度,才能计算各向异性效应,但是这将增加施工成本,所以煤层各向异性的影响一般被忽略了。笔者之前[21-22]初步研究了TI介质煤层槽波波场,发现VTI(Vertical Transverse Isotropy)介质和各向同性介质的Love槽波在速度上有较大差别,同时计算了TI介质多层地层Love槽波和Rayleigh槽波频散曲线[23-24],模拟了三维黏弹TI介质煤层的槽波传播,分析了槽波波场[25]。总体来说,目前将黏弹和各向异性两种性质结合起来的黏弹各向异性煤层介质中的槽波研究仍然较少。
煤层作为沉积岩,为周期薄互层VTI介质,煤的裂缝在地应力作用下常会形成近垂直的裂隙系统,煤层又可简化为HTI(Horizontal Transverse Isotropy)介质。对具有倾斜对称轴的TTI(Tilted Transverse Isotropic)煤层介质,仍可沿着煤层方向建立坐标系,仍是VTI或HTI介质。笔者以弱各向异性煤层为研究对象,应用Thomsen等效介质理论[26],采用Kelvin-Voigt黏弹性模型,建立黏弹TI介质理论模型,用于研究该介质Love槽波频散与衰减特征。
1 黏弹TI介质理论
1.1 TI介质模型
TI介质有轴对称性(图1),具有垂直对称轴称为VTI介质,具有水平对称轴称为 HTI介质,裂隙近垂直方向发育的煤层属于HTI介质[23]。对具有倾斜对称轴的TTI煤层介质,沿着煤层方向建立坐标系,仍是VTI或HTI介质。
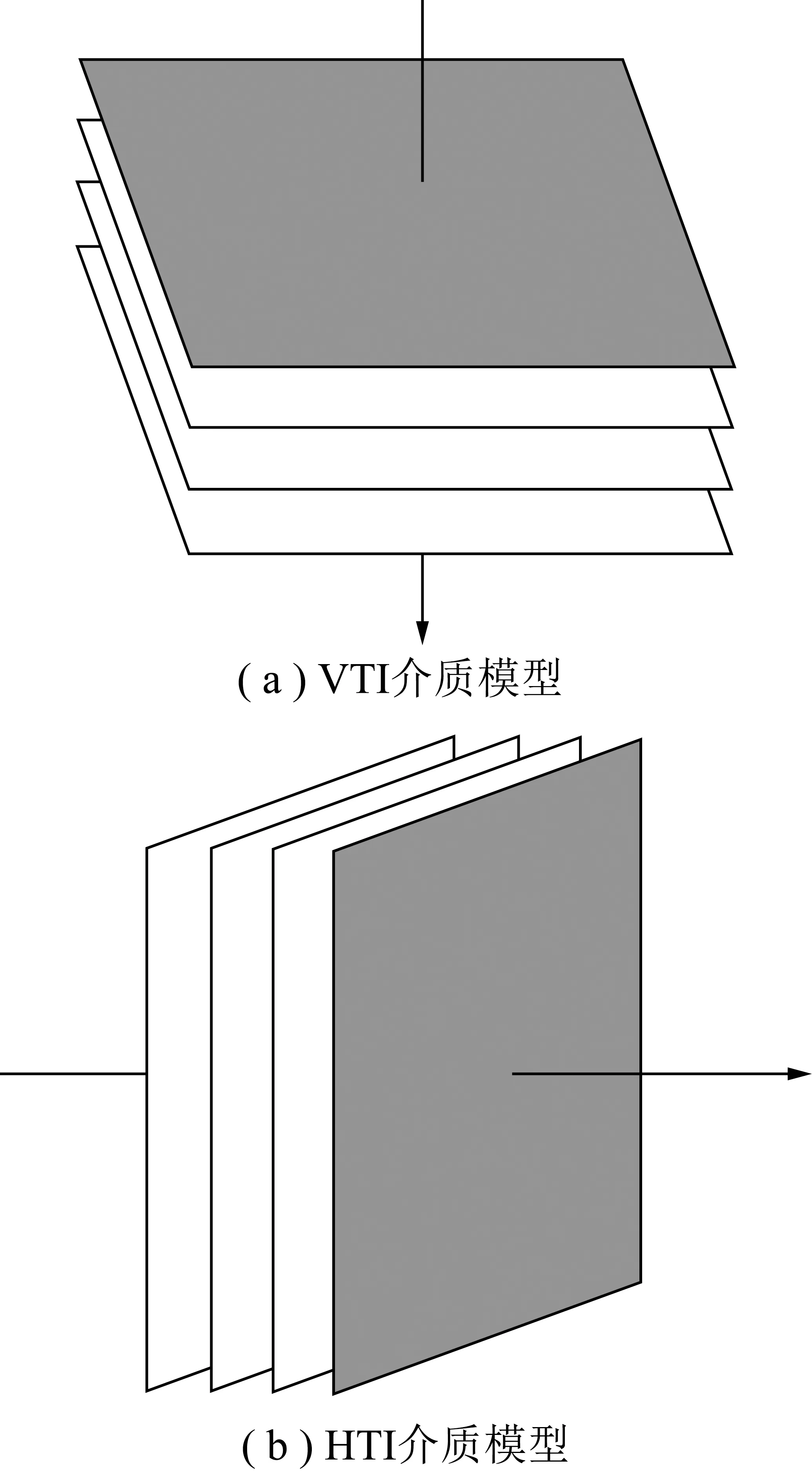
图1 TI介质模型示意Fig.1 Schematic diagrams of TI media
TI介质有5个弹性参数,与Love槽波相关的弹性参数有C44,C66,对VTI介质有
(1)
对HTI介质有

(2)
式中,ρ为介质密度;vS为qSV波和SH波垂直方向传播速度;γ为VTI介质Thomsen系数;γV为HTI介质Thomsen系数,表示横波各向异性。
1.2 黏弹介质模型
黏弹性介质模型采用Kelvin-Voigt模型,该模型由应变和应变变化率2部分组成,可看作将1个弹簧元件和1个阻尼器并联构成。该模型很容易和各向异性弹性矩阵结合,形成简洁的应力与应变本构方程,同时能取得很好的近似效果。
Kelvin-Voigt黏弹性介质应力向量σ和应变向量ε的本构关系为
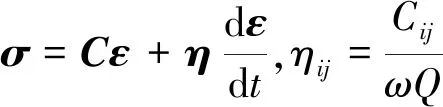
(3)
式(3)即为黏弹各向异性介质本构方程,其中,C为弹性矩阵,表征各向异性,与Thomsen参数可相互转化;η为黏滞矩阵,表征黏弹性,是品质因子Q和弹性矩阵C的函数(η11,η13,η33对应纵波品质因子Qp;η44,η66对应横波品质因子Qs);ω为圆频率。


(4)

(5)
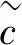
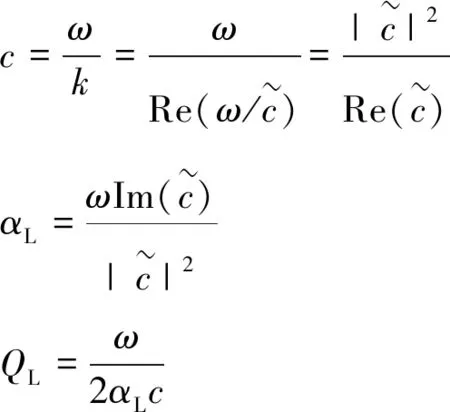
(6)
2 黏弹TI介质3层模型煤层Love槽波频散与衰减计算
笔者以常用的3层水平介质为模型,重点研究TI介质Love槽波频散方程。
VTI介质对称轴的方向为垂直方向z轴,xoy面是各向同性,垂直面xoz,yoz面是不同薄互层断面,为各向异性且性质相同,因此求解xoz平面Love槽波频散方程即可。HTI介质对称轴的方向设为x轴,垂直方向为z轴,则xoz平面体现了HTI介质典型性质,各向异性最大,yoz平面是各向同性,其他方向的垂直面各向异性大小介于这两个面之间,这些面内各种波耦合在一起,求解比较复杂,笔者主要求xoz平面内的HTI介质Love槽波频散方程。
2.1 黏弹TI介质Love槽波理论频散方程求解
在xoz平面,HTI介质和VTI介质的SH波波动方程形式相同,为
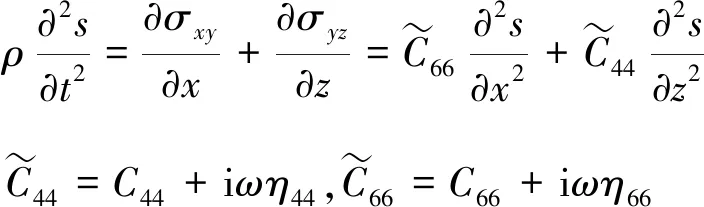
(8)
其中,s为位移;σ为应力。方程的平面波通解为s=s0eβzeiω(t-x/c),其中s0为初始位移;β为振幅随深度指数衰减的系数;c为波相速度;x为传播距离。
图2为3层水平层状TI介质煤层模型,上、下弹性半空间为围岩。上围岩的密度、垂向横波速度、弹性参数、横波品质因子分别为ρ1,vs1,C441,C661,Qs1;下围岩为ρ3,vs3,C443,C663,Qs3;中间低速夹层为煤层,其相应参数为ρ2,vs2,C442,C662,Qs2,煤层厚度为2d。坐标原点位于煤层中心,z轴垂直向下,x轴平行于煤层顶界面。

图2 黏弹TI介质3层非对称水平层状煤层模型Fig.2 Asymmetrical three-layer coal seam model of viscoelastic and TI medium
黏弹各向异性水平层状介质中槽波频散特征方程和各向异性介质有相同的形式,不同的是将波数、速度、弹性常数从实数域扩展到复数域。根据连续边界条件和广义胡克定律[22-23],得到Love槽波频散方程的2个解:
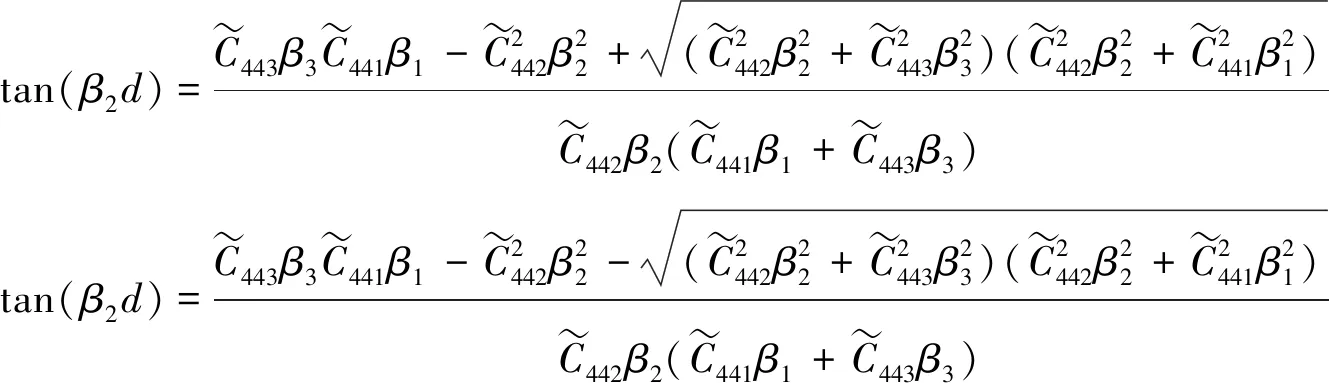
(9)
式中,β1,β2,β3分别为3层介质中振幅随深度指数衰减的系数,有

(10)
若上、下围岩相同,3层对称模型Love槽波解可统一为

(11)
当n=0时称为基阶相速度频散曲线,n=1时称为一阶频散曲线,依次类推。群速度可由相速度推导出来[1]。
2.2 黏弹TI介质Love槽波频散和衰减性质分析
首先研究煤层各向异性参数γ对槽波频散和衰减曲线的影响。以表1中的参数为例,计算黏弹TI介质煤层γ参数变化的0~3阶Love槽波各频散曲线(图3),γ=0为各向同性介质,γ≠0为各向异性介质。为重点研究煤层各向异性,将围岩设计为各向同性。由图3可看出,VTI介质速度频散曲线与各向同性介质差别较大,槽波速度值比各向同性大,HTI介质与各向同性介质槽波速度差别较小,VTI和HTI介质高阶Airy相位置与各向同性相比差别较大。对于槽波品质因子和衰减系数基阶曲线,VTI,HTI和各向同性介质3者差别小,高阶曲线差别稍大。槽波品质因子Airy相位置和速度频散曲线Airy相位置基本一致,此处槽波Q值最小,衰减系数在Airy相位置突然增大,之后线性增加,总体呈增长趋势。由此可见:各向异性参数γ对Love槽波品质因子和衰减系数值大小影响不大,对Airy相位置有一定影响,而且Airy相位置可从TI弹性介质群速度推测出来。

表1 黏弹TI介质3层对称模型γ参数变化Table 1 Variation of γ parameter in three-layer symmetric model of viscoelastic TI media
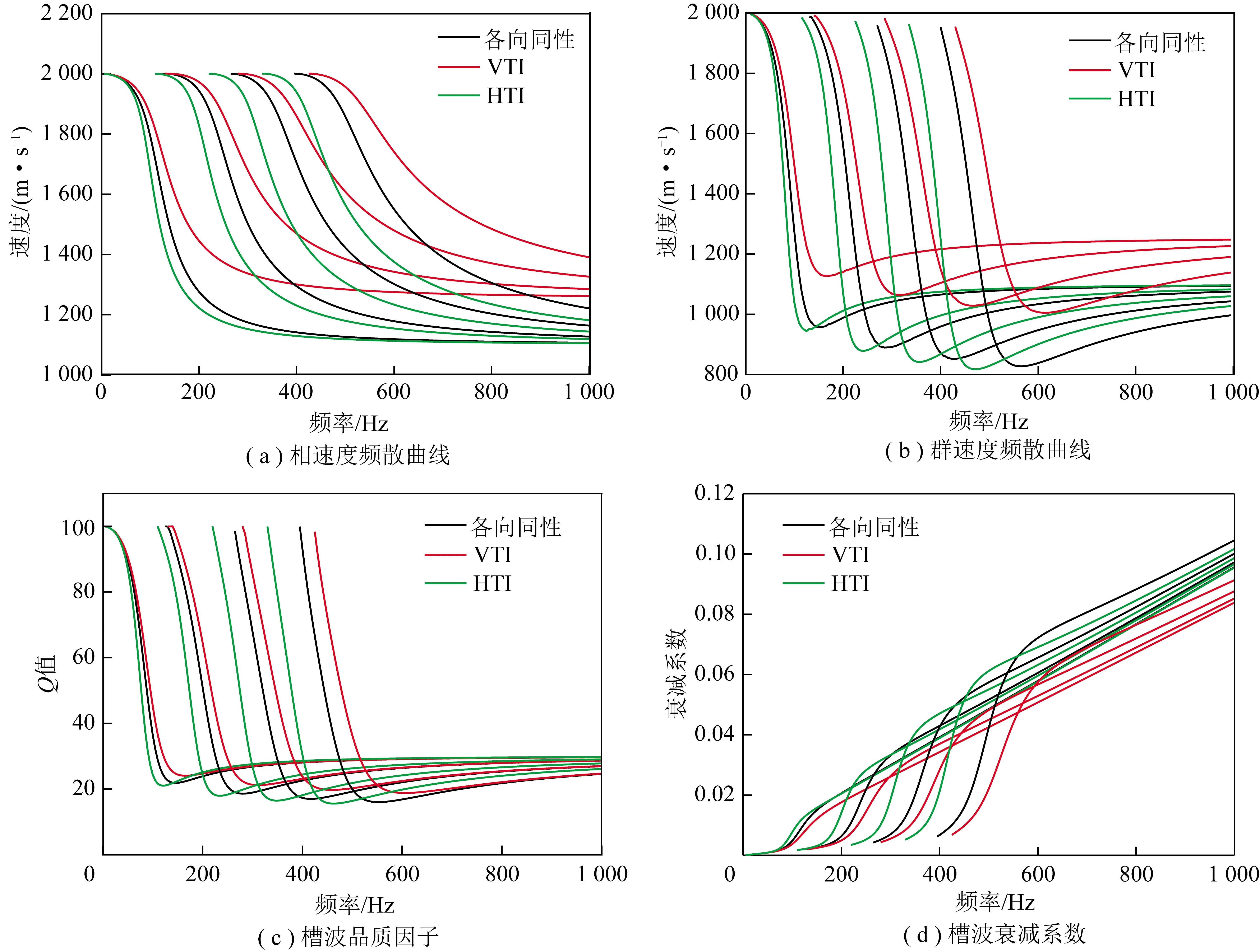
图3 黏弹TI介质3层对称模型γ参数变化Love槽波各曲线对比Fig.3 Comparison of the dispersion curves of Love channel wave with γ parameter changes in the three-layer symmetrical model of viscoelastic TI media
为研究煤层Qs值变化对槽波的影响,以表1中黏弹各向同性介质3层对称模型为基础,仅改变煤层Qs(表2),计算槽波频散和衰减曲线。可以看出(图4):煤层Qs改变对速度频散曲线改变很小,基阶几乎无变化;品质因子和衰减系数曲线变化很大,尤其煤层Qs=10时衰减系数增幅很大,说明煤层Qs较小时对衰减系数影响很大,槽波传播距离短。

表2 黏弹各向同性介质3层对称模型煤层品质因子变化Table 2 Variation of coal Qs parameter in three-layer symmetric model of viscoelastic and isotropy media

图4 黏弹各向同性介质3层对称模型煤层Qs变化 Love槽波各曲线对比Fig.4 Comparison of the dispersion curves of Love channel wave with coal Qs parameter changes in the three-layer symmetrical model of viscoelastic isotropic media
在地面三维地震勘探中,在地震波的频带范围(<200 Hz)内,一般认为品质因子Q值为常数,不随频率变化[27]。但是也有一些实验室表明有些岩层Q值与频率有关,MEISSNER[28]对海上频宽为300~6 000 Hz的数据分析表明Q与频率有关。RAIKES等[29]发现在10~375 Hz内Pierre页岩的Q值与频率有幂函数规律。JENG等[30]测量了浅地表疏松沉积层的Q值,结果表明在300 Hz以内Q值随频率变化,而且变化范围较大。对煤层Q值的测量多在实验室中进行,多采用频率高达100 kHz的超声波测量[4,14],测得的Q值大多在0~10,对煤层Q值是否随频率变化尚无定论。由于槽波频率高达500~600 Hz,且煤层裂隙多[31],笔者判断在0~1 000 Hz内煤层Q值随频率变化的可能性大。假设煤层Q值可能是频率的函数,笔者研究这种情况下槽波Q值的变化规律,先做下超前研究,另外也说明本文建立的理论是可以计算Q值随频率变化的情况。
为研究煤层Qs随频率变化对槽波的影响,以表1黏弹各向同性介质3层对称模型为基础,将煤层Qs随频率线性减小(一般频率越大,Qs越小[4,14]),其他参数不变,在0~1 000 Hz频率内煤层Qs分别从30降到20,10(表3),这是以前槽波研究没有做过的。可以看出(图5):相速度频散曲线基本不变,品质因子曲线各阶低频部分差异很小,随频率增加差异变大,煤层Qs随频率减小越快,品质因子值减小越多;
衰减系数曲线变化尤其明显,煤层Qs从30降到10的衰减系数值比其他2条曲线高频部分大很多。由此可知煤层Qs随频率变化对Love槽波影响较大,减小越快影响越大,当Qs减小到10,衰减系数值随频率呈几何增长。
3 三维黏弹TI介质槽波数值模拟
3.1 三维HTI介质一阶速度-应力弹性波方程
根据黏弹Kelvin-Voigt模型和Thomsen理论公式,可得出VTI介质一阶速度-应力弹性波方程:

(12)
黏弹HTI介质一阶速度-应力弹性波方程:

(13)
采用交错网格高阶有限差分法来模拟三维煤层槽波,对巷道自由界面采用镜像法处理[32],边界吸收采用完全匹配层法。
3.2 黏弹VTI介质槽波波场模拟
笔者[24]模拟了黏弹TI介质三维3层模型槽波波场,煤层横波品质因子Qs设为30,纵波品质因子Qp为50,不随频率改变,围岩设为各向同性,本文仍然以文献[24]模型为基础模型,但是将煤层Qs,Qp分别设为(10,30)和(20,40)两种情况,研究煤层品质因子对槽波波场传播的影响,围岩设为黏弹性。由于HTI和各向同性介质差别较小,笔者主要模拟VTI介质,具体设计如下:三维模型xyz方向的大小为200 m×200 m×25 m(图6),中间为煤层,煤厚5 m,两边是岩性相同的围岩,xyz方向网格大小1 m×1 m×0.25 m,时间采样间隔dt=0.05 ms。取煤层纵波速度1 900 m/s,横波速度1 100 m/s,密度1 300 kg/m3,煤层纵波品质因子Qp先设为30,横波品质因子Qs为10,纵波各向异性参数ε、纵波变异系数δ、横波各向异性参数γ为0.10,-0.10,0.15;顶、底板围岩纵波速度3 500 m/s,横波速度2 000 m/s,密度2 400 kg/m3,ε,γ,δ都为0,为各向同性介质,围岩纵波品质因子Qp为200,横波品质因子Qs为100。巷道有2条:一条在x=11~15 m,y=10~190 m,z=11~14 m处;另一条在x=186~190 m,y=10~190 m,z=11~14 m处,巷道断面4 m×3 m,内部设为真空。测线1(x=185 m,z=12.5 m)在右边的巷道壁上,测线2(y=100 m,z=12.5 m)过炮点(图6(b)中黑线)。炮点位置在煤层中央,水平坐标为x=16 m,y=100 m,如图6(b)中圆圈所示,震源采用主频150 Hz雷克子波,激发纵波。
图7为60 ms时的波场快照,图8为测线1的槽波记录,图9为测线2的槽波记录。图7中传播在最前面的是折射纵波,后面依次是折射横波、高阶Rayleigh槽波,最后面速度最慢的是基阶Rayleigh和Love槽波。60 ms时刻基阶槽波还很强,但当槽波传播到对面巷道时,测线1接收到的基阶槽波(图8)已经很弱,肉眼几乎看不到,整个过程在图9上看的更加清楚,随着槽波传播槽波能量减小很快,基阶Rayleigh槽波比高阶减小快。这些与笔者之前[24]模拟的结果有很大不同,由于他们取煤层Qs=30,基阶槽波衰减慢,测线1记录上能量仍然较强,而当本文取煤层Qs=10时,基阶槽波几乎衰减殆尽,Love槽波完全接收不到,只存在高速的高阶Rayleigh槽波。实际有些煤层接收不到Love槽波,原因可能就是煤层品质因子过低,对槽波的吸收衰减过强。在实际探测工作面构造中,接收不到槽波是槽波方法应用的一个难题,由本模拟结果笔者提出一个解决思路,即采用速度较高、衰减较小的高阶Rayleigh槽波(图8(c),图10(c))进行探测,此波经常被认为是围岩折射横波,实际应该两种波都有,由于该波在煤层中传播,所以可以用此波探测煤层中构造,弥补常规槽波方法的不足。

图6 含巷道煤层工作面模型Fig.6 Working face model of coal seam with roadways
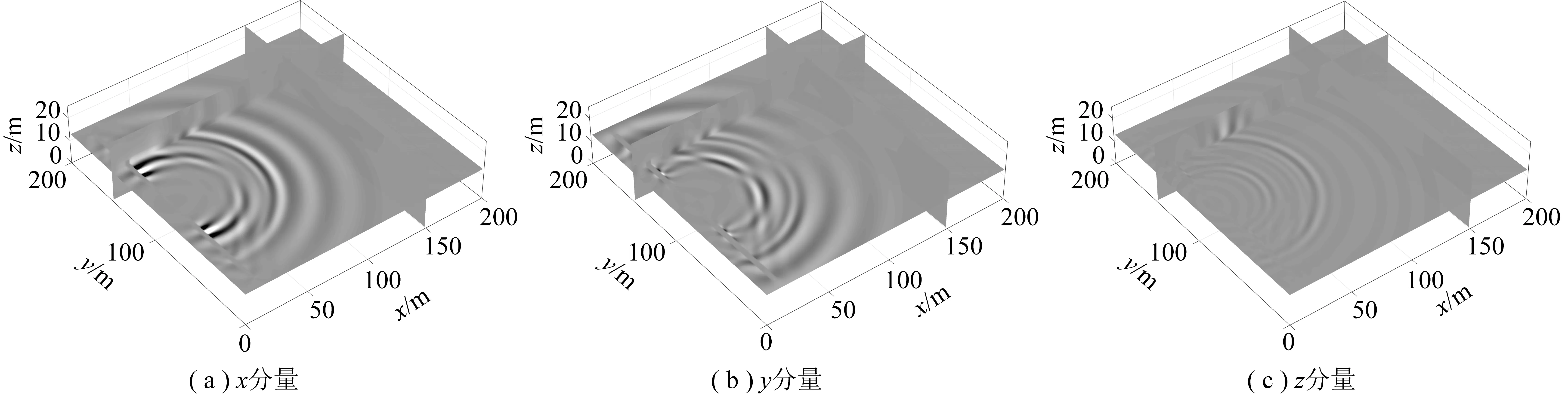
图7 60 ms波场快照(煤层Qs=10)Fig.7 Wave field snapshot at 60 ms(Qs=10)

图8 测线1槽波记录(煤层Qs=10)Fig.8 Channel wave record by survey line 1(Qs=10)
由于测线2过震源,测线2的y分量只含有Love型槽波,不含Rayleigh槽波,而x,z分量只含Rayleigh槽波。图10为采用F-K法提取的测线2 的频散图,可以看到一阶Rayleigh槽波强,Love槽波基本看不到明显的频散曲线形状。
再把煤层横波品质因子Qs=20,纵波品质因子Qp=40,分析槽波波场(图11~13)。测线1透射槽波记录接收有低速的基阶槽波(图11),y分量基阶槽波能量很强,以Love槽波为主(图13(b)),z分量基阶Rayleigh槽波能量小些,x分量基阶槽波能量较弱,这与煤层横波品质因子Qs=10的情况差别很大,后者几乎接收不到基阶槽波,这说明煤层Qs降低到10时对槽波的吸收衰减剧烈增加,本工作面宽度170 m,和实际工作面宽度接近,实际槽波透射工程中时常接收不到基阶槽波,推测原因很大可能是因为煤层Qs很小,不是一般认为的品质因子在30以上,这也是以前一直没搞清槽波不发育的主要原因之一。当然槽波不发育的另外一个原因也有可能是围岩和煤层物性差异较小,笔者针对围岩和煤层物性差异较大的情况。
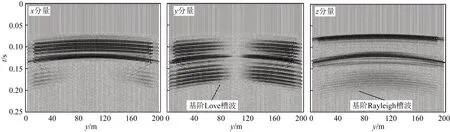
图11 测线1槽波记录(煤层Qs=20)Fig.11 Channel wave record by survey line 1(Qs=20)
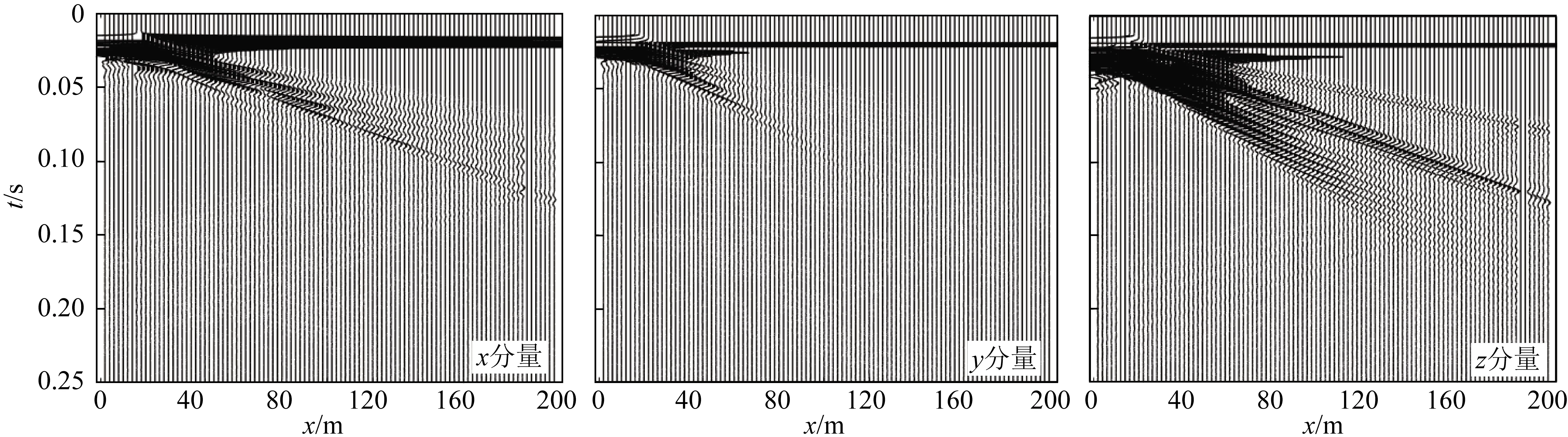
图12 测线2槽波记录(煤层Qs=20)Fig.12 Channel wave record by survey line 2(Qs=20)

图13 测线2槽波记录速度v-频率f域功率谱(煤层Qs=20)Fig.13 Power spectrums of channel wave records by survey line 2 in the v-f domain(Qs of coal seam is 20)
4 结 论
(1)对于槽波品质因子和衰减系数基阶曲线,VTI,HTI和各向同性介质3者差别小,高阶曲线差别稍大。各向异性参数γ对Love槽波品质因子和衰减系数值影响较小,对频散曲线Airy相位置有一定影响,频率有些偏移。
(2)煤层横波品质因子Qs对Love槽波速度频散曲线影响很小,但是对Love槽波品质因子和衰减系数曲线影响很大,尤其煤层Qs=10时衰减系数增幅很大,说明煤层Qs很小时对衰减系数影响很大,槽波衰减很快,槽波传播距离短。
(3)假设煤层Qs随频率变化,当煤层Qs随频率线性减小时,Love槽波速度频散曲线基本不变,品质因子曲线各阶低频部分差异很小,高频部分差异变大,煤层Qs随频率减小越快,槽波衰减系数增长越大,当Qs减小到10,衰减系数随频率呈几何增长。
(4)通过三维波场模拟,发现煤层品质因子Qs=10时Love槽波和基阶Rayleigh槽波衰减很快,接收不到透射槽波,而煤层Qs=20时,透射Love槽波和基阶Rayleigh槽波能量较强,实际工程中时常接收不到这些波,推测原因很大可能是这些煤层Qs很小,大大低于常规煤层。
(5)在实际探测工作面构造中,对于接收不到Love槽波和基阶Rayleigh槽波的情形,可以利用速度较高、衰减相对较小的高阶Rayleigh槽波探测,由于该波在煤层中传播,所以可以用此波探测煤层中构造,弥补常规槽波方法的不足。
以后还需测试分析实际煤层结构对煤层品质因子和槽波波场的影响,并和实际槽波数据做对比,为实际探测应用提供指导。
